Войти
Эта Тольяттинская поверхность является алгебраической поверхностью градуса пять. Изображение представляет собой часть его реального геометрического места.Алгебраическая геометрия - это ветвь математики, классически изучающая нули многомерных многочленов. Современная алгебраическая геометрия основана на использовании абстрактных алгебраических методов, в основном из коммутативной алгебры, для решения геометрических задач об этих наборах нулей.
Основными объектами изучения алгебраической геометрии являются алгебраические многообразия, которые являются геометрическими проявлениями решений систем полиномиальных уравнений. Примеры наиболее изученных классов алгебраических разновидностей: плоские алгебраические кривые, которые включают прямые, круги, параболы, эллипсы, гиперболы, кубические кривые типа эллиптические кривые и кривые четвертой степени, такие как лемнискаты и овалы Кассини. Точка на плоскости принадлежит алгебраической кривой, если ее координаты удовлетворяют заданному полиномиальному уравнению . Основные вопросы включают изучение точек, представляющих особый интерес, таких как особые точки, точки перегиба и точки на бесконечности. Более сложные вопросы связаны с топологией кривой и соотношениями между кривыми, заданными различными уравнениями.
Алгебраическая геометрия занимает центральное место в современной математике и имеет множество концептуальных связей с такими разнообразными областями, как комплексный анализ, топология и теория чисел. Изначально изучение систем полиномиальных уравнений с несколькими переменными, предмет алгебраической геометрии начинается там, где решение уравнения заканчивается, и становится еще более важным понять внутренние свойства совокупности решений системы уравнений, чем найти конкретное решение; это ведет к некоторым из самых глубоких областей математики, как концептуально, так и с точки зрения техники.
В ХХ веке алгебраическая геометрия разделилась на несколько частей.
Большая часть развития основного направления алгебраической геометрии произошла в 20 веке. в абстрактных алгебраических рамках, с возрастающим акцентом на «внутренних» свойствах алгебраических многообразий, не зависящих от какого-либо конкретного способа вложения разнообразия в объемлющее координатное пространство; это происходит параллельно с развитием топологии , дифференциальной и сложной геометрии. Одним из ключевых достижений этой абстрактной алгебраической геометрии является теория схем Гротендика , которая позволяет использовать теорию пучков для изучения алгебраических многообразий очень похожим образом. его использованию при изучении дифференциальных и аналитических многообразий. Это достигается за счет расширения понятия точки: в классической алгебраической геометрии точка аффинного многообразия может быть идентифицирована с помощью Nullstellensatz Гильберта с максимальным идеалом координатное кольцо, а все точки соответствующей аффинной схемы являются первичными идеалами этого кольца. Это означает, что точка такой схемы может быть как обычной точкой, так и подмногообразием. Этот подход также позволяет объединить язык и инструменты классической алгебраической геометрии, в основном связанной с комплексными точками, и теории алгебраических чисел. Доказательство Уайлса давней гипотезы, называемой последней теоремой Ферма, является примером силы этого подхода.
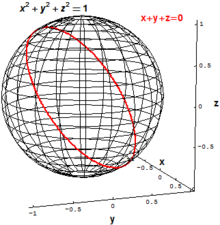Сфера и наклонный круг В классической алгебраической геометрии основные объекты, представляющие интерес, - это исчезающие множества наборов многочленов, что означает множество всех точек at одновременно удовлетворяют одному или нескольким полиномиальным уравнениям. Например, двухмерная сфера радиуса 1 в трехмерном евклидовом пространстве Rможет быть определена как набор всех точек (x, y, z) с
A "наклонный" круг в R может быть определен как набор всех точек (x, y, z), которые удовлетворяют двум полиномиальным уравнениям
Сначала мы начнем с поля k. В классической алгебраической геометрии этим полем всегда были комплексные числа C, но многие из тех же результатов верны, если мы предположим только, что k является алгебраически замкнутым. Мы рассматриваем аффинное пространство размерности n над k, обозначенное A (k) (или, проще говоря, A, когда k ясно из контекста). Когда фиксируется система координат, можно идентифицировать A (k) с k. Цель отказа от работы с k состоит в том, чтобы подчеркнуть, что мы «забываем» структуру векторного пространства, которую несет k.
Функция f: A→ Aназывается полиномиальной (или регулярной), если ее можно записать как полином, то есть если в k есть полином p [x 1,..., x n ] такие, что f (M) = p (t 1,..., t n) для каждой точки M с координатами (t 1,..., t n) в A . Свойство функции быть полиномиальной (или регулярной) не зависит от выбора системы координат в A.
. При выборе системы координат регулярные функции на аффинном n-пространстве могут быть отождествлены с кольцом полиномиальные функции от n переменных над k. Следовательно, набор регулярных функций на A представляет собой кольцо, которое обозначается k [A ].
Мы говорим, что многочлен обращается в нуль в точке, если вычисление его в этой точке дает ноль. Пусть S - набор многочленов от k [A ]. Исчезающее множество S (или исчезающее множество или нулевое множество) - это множество V (S) всех точек в A, где каждый многочлен из S равен нулю. Символически
Подмножество A, которое является V (S) для некоторого S, называется алгебраическим множеством. Буква V означает разнообразие (конкретный тип алгебраического множества будет определен ниже).
Учитывая подмножество U из A, можно ли восстановить набор полиномов, которые его порождают? Если U - любое подмножество A, определите I (U) как набор всех многочленов, исчезающее множество которых содержит U. I означает идеал : если два многочлена f и g оба обращаются в нуль на U, то f + g обращается в нуль на U, и если h - любой многочлен, то hf обращается в нуль на U, поэтому I (U) всегда является идеалом кольца многочленов k [A ].
Два естественных вопроса, которые следует задать:
Ответ на первый вопрос дается путем введения топологии Зарисского, топологии на A, замкнутые множества - это алгебраические множества, которые непосредственно отражают алгебраическую структуру k [A ]. Тогда U = V (I (U)) тогда и только тогда, когда U - алгебраическое множество или, что эквивалентно, замкнутое по Зарисскому множество. Ответ на второй вопрос дает Nullstellensatz Гильберта. В одной из своих форм он говорит, что I (V (S)) - это радикал идеала, порожденного S. На более абстрактном языке существует связь Галуа, дающая увеличиться до двух операторов закрытия ; они могут быть идентифицированы и, естественно, играют основную роль в теории; пример разработан в связи Галуа.
По разным причинам мы не всегда можем захотеть работать со всем идеалом, соответствующим алгебраическому множеству U. Базисная теорема Гильберта подразумевает, что идеалы в k [A ] всегда конечно порождены.
Алгебраическое множество называется неприводимым, если оно не может быть записано как объединение двух меньших алгебраических множеств. Любое алгебраическое множество - это конечное объединение неприводимых алгебраических множеств, и это разложение единственно. Таким образом, его элементы называются неприводимыми компонентами алгебраического множества. Неприводимое алгебраическое множество также называется многообразием. Оказывается, алгебраическое множество является многообразием тогда и только тогда, когда его можно определить как исчезающее множество первичного идеала кольца многочленов.
Некоторые авторы не проводят четкого различия между алгебраическими множествами и разновидностями и используют неприводимое разнообразие, чтобы проводить различие, когда это необходимо.
Так же, как непрерывные функции являются естественными отображениями на топологических пространствах, а гладкие функции являются естественными отображениями на дифференцируемых многообразиях существует естественный класс функций на алгебраическом множестве, называемых регулярными функциями или полиномиальными функциями. Регулярная функция на алгебраическом множестве V, содержащаяся в A, является ограничением на V регулярной функции на A . Для алгебраического множества, определенного на поле комплексных чисел, регулярные функции гладкие и даже аналитические.
Может показаться неестественно ограничивающим требование, чтобы регулярная функция всегда распространялась на окружающее пространство, но это очень похоже на к ситуации в нормальном топологическом пространстве, где теорема о расширении Титце гарантирует, что непрерывная функция на замкнутом подмножестве всегда распространяется на внешнее топологическое пространство.
Как и в случае с регулярными функциями на аффинном пространстве, регулярные функции на V образуют кольцо, которое мы обозначим через k [V]. Это кольцо называется координатным кольцом V.
Поскольку регулярные функции на V происходят от регулярных функций на A, существует связь между координатными кольцами. В частности, если регулярная функция на V является ограничением двух функций f и g в k [A ], то f - g является полиномиальной функцией, которая является нулевой на V и, следовательно, принадлежит I (V). Таким образом, k [V] может быть идентифицировано с k [A ] / I (V).
Используя регулярные функции из аффинного многообразия в A, мы можем определить регулярные отображения из одного аффинного многообразия в другое. Сначала мы определим регулярное отображение многообразия в аффинное пространство: пусть V - многообразие, содержащееся в A . Выберите m обычных функций на V и назовите их f 1,..., f m. Мы определяем регулярное отображение f из V в A, полагая f = (f 1,..., f m). Другими словами, каждый f i определяет одну координату диапазона f.
Если V ′ - это разнообразие, содержащееся в A, мы говорим, что f является регулярным отображением из V в V ′, если диапазон f содержится в V ′.
Определение регулярных отображений применимо также к алгебраическим множествам. Регулярные отображения также называются морфизмами, поскольку они превращают совокупность всех аффинных алгебраических множеств в категорию , где объекты являются аффинными алгебраическими множествами, а морфизмы являются регулярными отображениями. Аффинные многообразия - это подкатегория категории алгебраических множеств.
Если дано регулярное отображение g из V в V ′ и регулярная функция f из k [V ′], то f ∈ g ∈ k [V]. Отображение f → f ∘ g является кольцевым гомоморфизмом из k [V ′] в k [V]. Наоборот, всякий гомоморфизм колец из k [V ′] в k [V] определяет регулярное отображение из V в V ′. Это определяет эквивалентность категорий между категорией алгебраических множеств и противоположной категорией конечно порожденных редуцированных k-алгебр. Эта эквивалентность является одной из отправных точек теории схем.
В отличие от предыдущих разделов, этот раздел касается только многообразий, а не алгебраических множеств. С другой стороны, определения естественным образом распространяются на проективные многообразия (следующий раздел), поскольку аффинное многообразие и его проективное пополнение имеют одно и то же поле функций.
Если V - аффинное многообразие, его координатное кольцо является областью целостности и, таким образом, имеет поле дробей, которое обозначается k (V) и называется полем рациональных функций на V или, вкратце, функционального поля поля V. Его элементы являются ограничениями на V рациональных функций над аффинным пространством, содержащим V. область рациональной функции f - это не V, а дополнение подмногообразия (гиперповерхности), где знаменатель f равен нулю.
Как и в случае с обычными отображениями, можно определить рациональное отображение из многообразия V в многообразие V '. Как и в случае с регулярными отображениями, рациональные отображения из V в V 'могут быть отождествлены с гомоморфизмами поля из k (V') в k (V).
Две аффинные разновидности бирационально эквивалентны, если между ними есть две рациональные функции, обратные друг другу в областях, где обе определены. Эквивалентно, они бирационально эквивалентны, если их функциональные поля изоморфны.
Аффинное многообразие - это рациональное многообразие, если оно бирационально эквивалентно аффинному пространству. Это означает, что разнообразие допускает рациональную параметризацию, то есть параметризацию с помощью рациональных функций. Например, круг уравнения 
, что также можно рассматривать как рациональное карта от линии до круга.
Проблема разрешения особенностей состоит в том, чтобы знать, является ли каждое алгебраическое многообразие бирационально эквивалентным многообразию, проективное пополнение которого неособо (см. Также гладкое пополнение ). Она была разрешена положительно в характеристике 0 Хейсуке Хиронака в 1964 году и до сих пор не решена в конечной характеристике.
Парабола (y = x, красный) и кубическая (y = x, синий) в проективном пространстве Так же, как формулы для корней многочленов второй, третьей и четвертой степени предлагают расширить действительные числа до более алгебраически полного набора комплексных чисел, многие свойства алгебраических многообразий предполагают расширение аффинного пространства до более геометрически полного проективного пространства. В то время как комплексные числа получаются добавлением числа i, корня многочлена x + 1, проективное пространство получается добавлением соответствующих точек «на бесконечности», точек, где могут пересекаться параллельные прямые.
Чтобы понять, как это могло произойти, рассмотрим многообразие V (y - x). Если нарисовать его, то получится парабола. Когда x стремится к положительной бесконечности, наклон прямой от начала координат до точки (x, x) также стремится к положительной бесконечности. Когда x стремится к отрицательной бесконечности, наклон той же прямой стремится к отрицательной бесконечности.
Сравните это с разнообразием V (y - x). Это кубическая кривая. Когда x стремится к положительной бесконечности, наклон прямой от начала координат до точки (x, x), как и раньше, стремится к положительной бесконечности. Но в отличие от предыдущего, когда x стремится к отрицательной бесконечности, наклон той же прямой также стремится к положительной бесконечности; полная противоположность параболе. Таким образом, поведение V (y - x) «на бесконечности» отличается от поведения «на бесконечности» V (y - x).
Рассмотрение проективного завершения двух кривых, которое является их продолжением «на бесконечности» в проективной плоскости, позволяет нам количественно оценить эту разницу: бесконечно удаленная точка параболы - это регулярная точка , касательная к которой представляет собой бесконечно удаленную линию , а бесконечно удаленную точку кубической кривой представляет собой куспид. Кроме того, обе кривые рациональны, поскольку они параметризованы x, и теорема Римана-Роха подразумевает, что кубическая кривая должна иметь особенность, которая должна находиться на бесконечности, поскольку все ее точки в аффинном пространстве являются регулярными.
Таким образом, многие свойства алгебраических многообразий, включая бирациональную эквивалентность и все топологические свойства, зависят от поведения «на бесконечности», и поэтому естественно изучать многообразия в проективном пространстве. Более того, введение проективных методов сделало многие теоремы алгебраической геометрии проще и точнее: например, теорема Безу о количестве точек пересечения между двумя многообразиями может быть сформулирована в наиболее точной форме только в проективном пространстве. По этим причинам проективное пространство играет фундаментальную роль в алгебраической геометрии.
В настоящее время проективное пространство Pразмерности n обычно определяется как набор прямых, проходящих через точку, рассматриваемую как начало координат, в аффинном пространстве размерности n + 1, или эквивалентно набору векторных линий в векторном пространстве размерности n + 1. Когда система координат была выбрана в пространстве размерности n + 1, все точки линии имеют одинаковый набор координат, вплоть до умножение на элемент k. Это определяет однородные координаты точки P как последовательность из n + 1 элементов базового поля k, определенного с точностью до умножения на ненулевой элемент k (то же для всей последовательности).
Многочлен от n + 1 переменных обращается в нуль во всех точках прямой, проходящей через начало координат, тогда и только тогда, когда он однороден. В этом случае говорят, что многочлен обращается в нуль в соответствующей точке P . Это позволяет нам определить проективное алгебраическое множество в P как множество V (f 1,..., f k), где конечный набор однородные многочлены {f 1,..., f k } равны нулю. Как и для аффинных алгебраических множеств, существует биекция между проективными алгебраическими множествами и редуцированными однородными идеалами, которые их определяют. Проективные многообразия - это проективные алгебраические множества, определяющий идеал которых прост. Другими словами, проективное многообразие - это проективное алгебраическое множество, однородное координатное кольцо которого является областью целостности, причем кольцо проективных координат определяется как фактор градуированного кольца или многочленов от n + 1 переменных однородным (приведенным) идеалом, определяющим многообразие. Любое проективное алгебраическое множество можно однозначно разложить в конечное объединение проективных многообразий.
Единственные регулярные функции, которые могут быть правильно определены на проективном многообразии, - это постоянные функции. Таким образом, это понятие не используется в проективных ситуациях. С другой стороны, поле рациональных функций или функциональное поле является полезным понятием, которое, как и в аффинном случае, определяется как набор частных двух однородных элементов одной степени в однородном координатном кольце.
Реальная алгебраическая геометрия - это изучение вещественных точек алгебраических многообразий.
Тот факт, чтополе действительных чисел является упорядоченным полем, нельзя игнорировать в таком исследовании. Например, кривая уравнения 
.
Одной из сложных проблем реальной алгебраической геометрии является нерешенная шестнадцатая проблема Гильберта : решить, какие положения возможны для овалов неособой плоской кривой степени 8.
Можно датировать происхождение вычислительной алгебраической геометрии встречей EUROSAM'79 (Международный симпозиум по символьным и алгебраическим манипуляциям), состоявшейся в Марселе, Франция, июнь 1979 года. На этой встрече
. Использование одного или нескольких алгоритмов, связанных с использованием одного или нескольких алгоритмов.
Основная часть математической теории, дополняющая символические методы, под названием числовая алгебраическая геометрия, была обеспечена в течение последних нескольких десятилетий. Основным вычислительным методом является продолжение гомотопии. Это поддерживает, например, модель вычисления с плавающей запятой для решения задач алгебраической геометрии.
A Базис Грёбнера - это система образующих полиномиального идеала, вычисление которого позволяет вывести многие свойства аффинного алгебраического множества оснований идеалом.
Для идеала I, определяющего алгебраическое множество V:
Вычисления в базисе Грёбнера не позволяют напрямую вычислить первичное разложение I или простые идеалы, определяющие неприводимое совокупность компонентов V, но большинство алгоритмов для Алгоритмы, не основанные на базисах Грёбнера, используют регулярные цепочки, но в некотором количестве ых чрезвычайных ситуаций могут потребоваться базисы Грёбнера.
Считается, что базы Грёбнера сложно вычислить. Фактически, они могут содержать, в худшем случае, многочлены, дипломы являются дважды экспоненциальной по количеству числа, и несколько многочленов, которые также являются дважды экспоненциальными. Однако это только наихудший случай сложности, оценка сложности алгоритма Лазарда 1979 года может использовать часто. Алгоритм Фогера F5 осознает эту сложность, так как его рассматривать как усовершенствование алгоритма Лаз 1979 года. Отсюда следует, что наилучшие реализации позволяют выполнять вычисления с алгебраическими множествами степени более 100 почти рутинно. Это означает, что в настоящее время означает сложность вычислений базиса Грёбнера связана с внутренней сложностью задачи.
CAD - это алгоритм, который был введен в 1973 г. Дж. Коллинзом для реализации с приемлемой сложностью теоремы Тарского - Зайденберга на исключение квантора по действительному числу.
Эта теорема касается формул логики первого порядка, атомарные формулы которой являются полиноми равенствами или неравенствами между полиномами с действующими коэффициентами. Эти формулы, таким образом, представляют собой формулы, которые могут быть построены из атомарных формул с помощью логических операторов и (∧) или (∨), а не (¬), для всех (∀) и существует (). Теорема Тарского утверждает, что по такой формуле можно вычислить вычисленную формулу без квантора (∀, ∃).
Сложность САПР двукратно экспоненциальна по количеству чисел. Это означает, что САПР теоретически позволяет решить любую проблему реальной алгебраической геометрии, которая может быть выражена такой формулой, то есть почти все проблемы, касающиеся явно заданных множеств и полуалгебраических множеств.
В то время как вычисление базиса Грёбнера имеет двойную экспоненциальную сложность только в редких случаях, CAD всегда такую высокую сложность. Это означает, что большинство полиномов, появляющихся во входных данных, не являются линейными, это не может решить проблемы с более чем четырьмя переменными.
С 1973 года большая часть исследований по этой теме посвящена либо совершенствованию САПР, либо поиску альтернативных алгоритмов в особых случаях, представляющих общий интерес.
В качестве примера современного уровня техники существуют эффективные алгоритмы для поиска по крайней мере точки в каждом связном компоненте полуалгебраического набора и, таким образом, для проверки того, является ли полуалгебраический набор пустым. С другой стороны, на практике САПР - алгоритм для подсчета количества подключенных компонентов.
Базовые общие алгоритмы вычислительной геометрии имеют двойной экспоненциальный наихудший случай сложность. Точнее, если d - максимальная степень входных полиномов, а n - количество число, их сложность не превосходит 
В течение 20 лет 20-го века были применены различные алгоритмы для введения конкретных решений подзадач с большей сложностью. Большинство из этих алгоритмов имеют сложность 
Среди этих алгоритмов, которые решают подзадачу задач, решаемых базисами Грёбнера, можно сослаться на Проверка того, является ли аффинное множество пустым, и решение неоднородных полиномиальных систем, которые имеют конечное число решений. Такие алгоритмы редко реализуются, потому что аналогичные алгоритмы F4 и F5 Фожера имеют лучшую практическую эффективность и вероятную или лучшую сложность (вероятно, потому что оценка сложных базовых алгоритмов для определенного класса записи - сложная задача, которая была выполнена только в нескольких случаях).
Основные алгоритмы реальной алгебраической геометрии, которые решают задачу, решаемую САПР, связаны с топологией полуалгебраических множеств. Можно сослаться на подсчет числа связанных компонентов, проверка того, есть ли две точки в одних и тех же компонентах, или вычисление стратификации Уитни реального алгебраического множества. Они имеют способность
Современные подходы к алгебраической геометрии переопределяют и эффективно расширяют круг основных объектов на различных уровнях общности до, формальных схем, инд-схемы, алгебраические пространства, алгебраические стеки и так далее. Необходимость в этом возникает уже из полезных идей многообразий, например, формальные функции Зарисского могут быть выполнены путем введения нильпотентных элементов в структурные кольца; рассмотрение пространств петель и дуг, построение факторов по групповым действиям и разработка формальных основ теории естественных пересечений и теории деформаций приводят к некоторым дальнейшим расширениям.
Наиболее примечательно то, что в конце 1950-х годов алгебраические разновидности были включены в концепцию схемы Александра Гротендика. Их локальные объекты - это аффинные схемы или простые спектры, которые являются локально окольцованными пространствами, которые образуют категорию, антиэквивалентную категории коммутативных колец с единицей, расширяя двойственность между категорией аффинных алгебраических многообразий над полем k и категорией конечно порожденных редуцированные k-алгебры. Склейка по топологии Зарисского; можно склеить в категории локально окольцованных пространств, но также, используя вложение Йонеды, в более абстрактную категорию предпучков множеств над категорией аффинных схем. Затем топология Зарисского в теоретико-множественном смысле заменяется топологией Гротендика. Гротендик представил топологии Гротендика, имея в виду более экзотические, но геометрически более тонкие и более чувствительные примеры, чем грубая топология Зариски, а именно этальная топология и две плоские топологии Гротендика: fppf и fpqc; в настоящее время стали известны и другие примеры, в том числе топология Нисневича. Кроме того, связки могут быть обобщены на стеки в смысле Гротендика, обычно с некоторыми дополнительными условиями представимости, приводящими к стекам Артина и, что еще более тонко, к стекам Делиня – Мамфорда, которые часто называют алгебраическими стеками..
Иногда другие алгебраические сайты заменяют категорию аффинных схем. Например, Николай Дуров ввел коммутативные алгебраические монады как обобщение локальных объектов в обобщенной алгебраической геометрии. В этой установке были реализованы версии тропической геометрии, абсолютной геометрии над полем из одного элемента и алгебраический аналог геометрии Аракелова.
Другое формальное обобщение возможно для универсальной алгебраической геометрии, в которой каждое разнообразие алгебр имеет свою собственную алгебраическую геометрию. Термин многообразие алгебр не следует путать с алгебраическим многообразием.
Язык схем, стеков и обобщений оказался ценным способом работы с геометрическими понятиями и стал краеугольным камнем современной алгебраической геометрии.
Алгебраические стопки могут быть дополнительно обобщены, и для многих практических вопросов, таких как теория деформации и теория пересечений, это часто наиболее естественный подход. Можно расширить сайт Гротендика аффинных схем до более высокого категориального сайта из производных аффинных схем, заменив коммутативные кольца на бесконечную категорию дифференциальные градуированные коммутативные алгебры, или симплициальных коммутативных колец, или аналогичная категория с подходящим вариантом топологии Гротендика. Можно также заменить предпучки множеств предпучками симплициальных множеств (или бесконечных группоидов). Затем, при наличии подходящего гомотопического механизма, можно развить понятие производного стека как такого предпучка в категории бесконечности производных аффинных схем, который удовлетворяет некоторой бесконечно категориальной версии аксиомы пучка (и, чтобы быть алгебраическим, индуктивно последовательность условий представимости). Категории модели Квиллена, категории Сигала и квазикатегории являются одними из наиболее часто используемых инструментов для формализации этого, что приводит к производной алгебраической геометрии, введенной школой Карлос Симпсон, в том числе Андре Хиршовиц, Бертран Тоен, Габриэль Веццози, Мишель Вакье и другие; и развитый далее Джейкобом Лурье, Бертраном Тоэном и. Другая (некоммутативная) версия производной алгебраической геометрии, использующая категории A-бесконечности, была разработана с начала 1990-х годов Максимом Концевичем и его последователями.
Некоторые корни алгебраической геометрии восходят к труд эллинистических греков V века до нашей эры. Задача Делана, например, заключалась в том, чтобы увеличить длину x так, чтобы куб со стороной x содержал тот же объем, что и прямоугольный ящик ab для данных сторон a и b. Менехм (около 350 г. до н.э.) рассмотрел проблему геометрически, пересекая пару плоских коник ay = x и xy = ab. Более поздняя работа, в III веке до нашей эры, Архимеда и Аполлония более систематически изучала проблемы на конических сечениях, а также включала использование координат. Мусульманские математики умели решать математические математические уравнения, математические формы, а затем воспроизводить результаты геометрически. Это было сделано, например, Ибн аль-Хайсам в 10 веке нашей эры. Вперед персидский математик Омар Хайям (родился в 1048 году эры) создал метод решения кубических уравнений путем пересечения параболы с кругом и, по-видимому, был первым представителем общую теорию кубических уравнений. Через несколько лет после Омара Хайяма Трактат Шараф ад-Дин ат-Туси об уравнениях был описан как «открытие начала алгебраической геометрии».
Такие методы геометрических построений к алгебраическим задачам были приняты рядом математиков эпохи Возрождения, таких как Джероламо Кардано и Никколо Фонтана «Тарталья» в своих исследованиях. кубического уравнения. Геометрический подход к проблемам построения, а не алгебраический, поддерживался большинством математиков XVI и XVII веков, особенно Блезом Паскалем, который выступал против использования алгебраических и аналитических методов в геометрии. Французские математики Франциск Виета и позже Рене Декарт и П де Ферма произвели революцию в общепринятом подходе к задачам, представив координатную геометрию. Их интересовали в первую функцию алгебраических кривых, например, те, которые определяют диофантовыми уравнениями (в случае Ферма), и алгебраическая переформулировка классических греческих работ по коникам и кубикам (в случае Декарт).
В тот же период Блез Паскаль и Жерар Дезарг подошли к геометрии с другой точки зрения, развивая синтетические понятия проективной геометрии. Паскаль и Дезарг также изучали кривые, но с чисто геометрической точки зрения: аналог греческой линейки и конструкции компаса. В конечном итоге победила аналитическая геометрия Декарта и Ферма, поскольку она предоставила математикам 18 века количественные инструменты, необходимые для изучения физических задач с использованием нового исчисления Ньютона и Лейбниц. Однако к концу 18-го века большая часть алгебраического характера координатной геометрии была отнесена к исчислению бесконечно малых Лагранжа и Эйлера.
Потребовалось совместное развитие неевклидовой геометрии и абелевых интегралов в 19 веке, чтобы вернуть старые алгебраические идеи в геометрическую форму. Первые из этих новых разработок были подхвачены Эдмондом Лагерром и Артуром Кэли, которые пытались установить обобщенные метрические свойства проективного пространства. Кэли ввел идею однородных полиномиальных форм, точнее квадратичных форм, на проективном пространстве. Вперед Феликс Клейн изучал проективную геометрию (наряду с другими типами геометрии) с точки зрения того, что геометрия в пространстве закодирована в определенном классе преобразований в пространстве. К концу XIX века проективные геометры изучали более общие виды преобразований фигур в проективном пространстве. Вместо проективных линейных преобразований, которые обычно рассматривались как фундаментальные клейновскую геометрию проективного пространства, они касались также бирациональных преобразований более высокой степени. Это более слабое понятие конгруэнтности позже привело членов итальянской школы алгебраической геометрии 20 века к классификации алгебраических поверхностей до бирационального изоморфизма.
Второе развитие в XIX века, что из абелевых интегралов, приведет Бернхарда Римана к развитию римановых поверхностей.
. В тот же период началась алгебраизация алгебраической геометрии через коммутативную алгебру. Основными преимуществами в этом направлении являются теорема Гильберта и Nullstellensatz Гильберта, которые являются причиной связи между алгебраической геометрией и коммутативной алгеброй, и теоремой Маколея. многомерный, который является результатом теории исключения. Вероятно, из-за размера вычислений, подразумеваемых многомерными результирующими, теория исключения была забыта в середине 20-го века, пока ее не обновили теорией сингулярностей и вычислительной алгебраической геометрией.
Б. Л. ван дер Варден, Оскар Зариски и Андре Вейль разработали основы алгебраической геометрии, основанные на современной коммутативной алгебре, включая теорию оценки. и теория идеалов. Одна из целей состояла в том, чтобы дать строгую основу для доказательства результатов итальянской школы алгебраической геометрии. В частности, эта школа систематически использовала понятие родовой точки без какого-либо точного определения, которое впервые было дано этими авторами в 1930-х годах.
В 1950-х и 1960-х годах Жан-Пьер Серр и Александр Гротендик переделали основы, используя теорию пучков. Позже, примерно с 1960 года, и в значительной степени во главе с Гротендиком, идея схем была разработана в сочетании с очень усовершенствованным аппаратом гомологических методов. После десятилетия стремительного развития в 1970-х эта область стабилизировалась, и были внесены новые приложения как в теорию чисел, так и в более классические геометрические вопросы алгебраических многообразий, сингулярностей, модули и формальные модули.
Важным классом многообразий, который нелегко понять непосредственно из определяющих их уравнений, являются абелевы многообразия, которые представляют собой проективные многообразия, точки которых образуют абелевы группа. Типичными примерами являются эллиптические кривые, у которых есть богатая теория. Они сыграли важную роль в доказательстве последней теоремы Ферма, а также используются в криптографии с эллиптическими кривыми.
. Параллельно с абстрактной тенденцией алгебраической геометрии, которая связана с общими утверждениями о многообразиях., были также разработаны методы эффективных вычислений с конкретными заданными разновидностями, что привело к новой области вычислительной алгебраической геометрии. Одним из основополагающих методов этой области является теория базисов Грёбнера, введенная Бруно Бухбергером в 1965 году. Другой метод основания, более специально посвященный реальной алгебраической геометрии, - это цилиндрическое алгебраическое разложение, введенное Джорджем Коллинзом в 1973 году.
См. также: производная алгебраическая геометрия.
аналитическое разнообразие определяется локально как набор общих решений нескольких уравнений, включающих аналитические функции. Это аналогично включенному понятию действительного или сложного алгебраического многообразия. Любое комплексное многообразие является аналитическим многообразием. Поскольку аналитические многообразия могут иметь особые точки, не все аналитические многообразия являются многообразиями.
Современная аналитическая геометрия по существу эквивалентна реальной и сложной алгебраической геометрии, как было показано Жан-Пьером Серром в своей статье GAGA, название которой Французский язык для алгебраической геометрии и аналитической геометрии. Тем не менее, эти две области остаются разными, поскольку методы доказательства разные, а алгебраическая геометрия включает также геометрию с конечной характеристикой.
Алгебраическая геометрия теперь находит применения в статистике, теория управления, робототехника, коды исправления ошибок, филогенетика и геометрическое моделирование. Есть также связи с теорией струн, теорией игр, сопоставлениями графов, солитонами и целочисленным программированием.
 | Викицитатник содержит цитаты, связанные с: Алгебраической геометрией |
