Базис Грёбнера

редактировать

Математическая конструкция в компьютерной алгебре

В математике, а более конкретно в компьютерная алгебра, вычислительная алгебраическая геометрия и вычислительная коммутативная алгебра, базис Грёбнера - это особый вид порождающего множества идеального в кольце многочленов K [x 1,.., x n ] над полем K. Базис Грёбнера позволяет легко получить важные важные свойства идеала и связанного с ним алгебраического разнообразия, например размерность и количество нулей, когда оно конечно. Вычисление базиса Грёбнера является одним из практических инструментов решения систем полиномиальных соотношений и вычислений изображений алгебраических множеств при проекциях или рациональных отображений.

. Грёбнера можно рассматривать как многомерное нелинейное обобщение как алгоритма Евклида для вычислений полиномиальных наибольших общих делителей, так и исключение Гаусса для линейных

Базисы Грёбнера были введены в 1965 году вместе с алгоритмом для их вычислений (алгоритм Бухбергера ) Бруно Бухбергером в его докторской диссертации. Тезис. Он назвал их в честь своего советника Вольфганга Грёбнера. В 2007 году Бухбергер получил за эту работу премию Ассоциации вычислительной техники Премия Пэрис Канеллакис за теорию и практику. Однако русский математик Николай Гюнтер ввел понятие в 1913 году, опубликованное в различных русских математических журналах. Эти статьи в степени игнорировались математическим сообществом до их повторного открытия в 1987 году Бодо Реншухом и др. Аналогичная концепция многомерного степенного ряда была независима Хейсуке Хиронака в 1964 году, который назвал их стандартными базами . Этот термин использовался некоторыми авторами также для обозначения базисов Грёбнера.

Теория базисов Грёбнера была развита авторами в различных направлениях. Он был обобщен на других структурах, таких как полиномы над кольцами главных идеалов или полиномиальными кольцами, а также на некоторых классах некоммутативных колец и алгебр, таких как алгебры Оре.

Содержание

1 Предпосылки
- 1.1 Кольцо многочленов
- 1.2 Мономиальное упорядочение
- 1.3 Редукция
2 Формальное определение
3 Пример и контрпример
4 Свойства и применение базисов Грёбнера
- 4.1 Равенство идеалов
- 4.2 Принадлежность и включение идеалов
- 4.3 Решения системы алгебраических уравнений
- 4.4 Размер, степень и ряд Гильберта
- 4.5 Исключение
- 4.6 Пересекающиеся идеалы
- 4.7 Имплициализация рациональной кривой
- 4.8 Насыщенность
  - 4.8.1 Определение насыщенности
  - 4.8.2 Вычисление насыщенности
- 4.9 Эффективное значение Nullstellensatz
- 4.10 Неявное выражение в более высоком измерении
5 Реализации
6 Области применения
- 6.1 Коды исправления ошибок
7 См. Также
8 Ссылки
9 Дополнительная литература
10 Внешние ссылки

Предпосылки

Кольцо многочленов

Базисы Грёбнера в основном для идеалов кольце многочленов $R = K [x 1,…, xn] {\ displaystyle R = K [x_ {1}, \ ldots, x_ {n}]}$ $R = K [x_1, \ ldots, x_n при условии$ над полем К. Хотя теория работает для любого поля, большинство вычислений в базисе выполняется либо когда K полем рациональных чисел, либо целыми числами по модулю простого числа.

A многочлен - это сумма $c 1 M 1 + ⋯ + cm M m {\ displaystyle c_ {1} M_ {1} + \ cdots + c_ {m} M_ {m}}$ $c_1M_1 + \ cdots + c_mM_m$ где $ci {\ displaystyle c_ {i}}$ $c_ {i}$ - ненулевые элементы K, а $M i {\ displaystyle M_ {i}}$ $M_ {i}$ - одночлены или "произведения мощности" число. Это означает, что моном M является продуктом $M = x 1 a 1 ⋯ xnan, {\ displaystyle M = x_ {1} ^ {a_ {1}} \ cdots x_ {n} ^ {a_ {n}}, }$ $M = x_1 ^ {a_1} \ cdots x_n ^ {a_n},$ где $ai {\ displaystyle a_ {i}}$ $a_ {i}$ - неотрицательные целые числа. Вектор $A = [a 1,…, an] {\ displaystyle A = [a_ {1}, \ ldots, a_ {n}]}$ $A = [a_1, \ ldots, a_n]$ называется вектором экспоненты M. Обозначения часто сокращаются как $x 1 a 1 ⋯ xnan = XA {\ displaystyle x_ {1} ^ {a_ {1}} \ cdots x_ {n} ^ {a_ {n}} = X ^ {A}}$ $x_1 ^ {a_1} \ cdots x_n ^ {a_n} = X ^ A$ . Мономы однозначно используют свои векторные показатели, поэтому компьютеры могут использовать методы векторных показателей, а полиномы - как списки показателей и их коэффициентов.

Если $F = {f 1,…, fk} {\ displaystyle F = \ {f_ {1}, \ ldots, f_ {k} \}}$ $F = \ {f_1, \ ldots, f_k \}$ является конечным набор многочленов в кольце многочленов R, идеал , порожденный F, представляет собой набор линейных комбинаций элементов из F с коэффициентами во всем R:

⟨f 1,…, fk⟩ = {∑ i = 1 кгифи | g 1,…, g k ∈ K [x 1,…, x n]}. {\ Displaystyle \ langle f_ {1}, \ ldots, f_ {k} \ rangle = \ left \ {\ sum _ {i = 1} ^ {k} g_ {i} f_ {i} \; | \; g_ {1}, \ ldots, g_ {k} \ in K [x_ {1}, \ ldots, x_ {n}] \ right \}.}

\ langle f_1, \ ldots, f_k \ rangle = \ left \ {\ sum_ {i = 1} ^ k g_i f_i \; | \; g_1, \ ldots, g_k \ in K [x_1, \ ldots, x_n] \ right \}.

Мономиальное упорядочение

Все операции, относящиеся к Грёбнеру базисы требуют выбора общего порядка на одночленах со свойствами совместимости с умножением. Для всех одночленов M, N, P,

$M ≤ N ⟺ MP ≤ NP {\ displaystyle M \ leq N \ Longleftrightarrow MP \ leq NP}$ $M \ leq N \ Longleftrightarrow MP \ leq NP$
$M ≤ MP {\ displaystyle M \ leq MP}$ $M \ leq MP$ .

Полный порядок, удовлетворяющий этим условиям, иногда называют допустимым порядком.

Эти условия подразумевают, что порядок правильным порядком, то есть каждая строгоывающая последовательность мономов конечна.

Хотя теория базиса Грёбнера не зависит от конкретного выбора допустимого мономиального порядка, три мономиальных порядка особенно важны для приложений:

Лексикографический порядок, обычно называемый лексическим или сплетением (для чистого лексического упорядочения).
Общий обратный лексикографический порядок, обычно называемый degrevlex.
Исключающий порядок, lexdeg.

Теория базиса Грёбнера была введена для лексикографической упорядочения. Вскоре стало понятно, что базис Грёбнера для degrevlex почти всегда намного проще вычислить, и что почти всегда легче вычислить базис lex-Гребнера сначала, вычислив базис degrevlex, используя «алгоритм изменения порядка». Когда требуется устранение, дегревлекс не подходит; могут быть как lexdeg, так и lexdeg, но, опять же, многие вычисления относительно просты с lexdeg и почти невозможны с lex.

Как только мономиальный порядок фиксирован, члены многочлена (произведение одночлена на его ненулевой коэффициент) естественным образом упорядочиваются по убыванию одночленов (для этого порядка). Это представление полинома в виде упорядоченного списка пар коэффициент-экспонента вектор каноническим представлением полиномов. Первый (наибольший) член полинома для этого порядка и соответствующий моном коэффициент называются соответственно главным, старшим мономом и старшим коэффициентом и обозначаются в этой статье lt (p), lm (p) и lc (п).

Редукция

Концепция редукции, также называемая многомерным делением или вычислением нормальной формы, является центральной для базиса Гребнера. теория. Это многомерное обобщение евклидова деления одномерных многочленов.

В этом разделе мы предполагаем фиксированный мономиальный порядок, который не будет определяться явно.

Учитывая два многочлена f и g, говорят, что f сводится на g, если некоторый моном m из f делится на главный моном lm (g) из g. Если m оказывается старшим мономом f, то говорят, что f приводимо по g. Если c - коэффициент при m в f и m = q lm (g), одношаговое уменьшение f на g - это операция, которая связывает с f многочлен

красный 1 ⁡ (f, g) = f - c lc ⁡ (g) qg. {\ displaystyle \ operatorname {red} _ {1} (f, g) = f - {\ frac {c} {\ operatorname {lc} (g)}} \, q \, g.}

\ operatorname {red} _1 (f, g) = f- \ frac {c} {\ operatorname {lc} (g)} \, q \, g.

Основные свойства Эта операция заключается в том, что полученный многочлен не содержит одночлена m и что одночлены больше m (для мономиального порядка) устанавливаются. Эта операция, как правило, не содержит однозначно; если несколько одночленов в f кратны lm (g), то можно произвольно выбрать, какой из них уменьшить. На практике для мономиального упорядочения лучше выбрать наибольший.

Исходное множество многочленов G, говорят, что f приводимо или сводимо по свинцу с помощью G, если оно сводимо или сводимо по свинцу, соответственно, с помощью элемента g из G. Если это так, тогда определяется $красный 1 ⁡ (f, G) = красный 1 ⁡ (f, g) {\ displaystyle \ operatorname {red} _ {1} (f, G) = \ operatorname {red} _ {1} (f, g) }$ $\ operatorname {red} _1 (f, G) = \ operatorname {red} _1 (f, g)$ . (Полное) сокращение f на G заключается в итеративном применении этого оператора $красный 1 {\ displaystyle \ operatorname {red} _ {1}}$ $\ operatorname {red} _1$ до получения многочлена $красный ⁡ (f, G) {\ displaystyle \ operatorname {red} (f, G)}$ $\ operatorname {red} ( f, G)$ , которая неприводима G. Она называется нормальной формой по G. В общем, эта форма не определена однозначно (это не каноническая форма ); эта неединственность является отправной точкой теории базисов Грёбнера.

Для вычислений базиса Грёбнера, за исключением конца, нет необходимости выполнять полную редукцию: достаточно сокращения опережения, что экономит большой объем вычислений.

Определение редукции показывает, что если h является сразу формой f по G, то мы имеем

f = h + ∑ g ∈ G qgg, {\ displaystyle f = h + \ sum _ {g \ in G} q_ {g} \, g,}

f = h + \ sum_ {g \ in G} q_g \, g,

где $qg {\ displaystyle q_ {g}}$ $q_g$ - многочлены. В случае одного многочленов, если G состоит из одного элемента g, то h - это остаток от евклидова деления f на g, q g - частное, а алгоритм деления - это в точности процесса снижения свинца. По этой причине некоторые используют используют многомерное деление вместо сокращения.

Формальное определение

Базис Грёбнера G идеала I в кольце многочленов R над полем генераторный агрегат из I, характеризующийся любым из следующих свойств, относительно некоторого мономиального порядка :

идеал, порожденный главными членами многочленов в I равен идеалу, порожденному главными членами G;
, главный член любого полинома в I делится на главный член любого полинома в G;
многомерного деления многочлена в кольце многочленов R на G дает уникальный остаток;
многомерное деление на G любого многочлена в идеал I дает остаток 0.

Все эти свойства эквивалентны; разные авторы используют разные в зависимости от выбранной темы. Последние два свойства выполняют вычисления в кольце множителей R / I с теми же возможностями, что и модульная арифметика. Важным фактом коммутативной алгебры является то, что базисы Грёбнера всегда могут быть вычислены для любого идеала, заданным конечным порождающим подмножеством.

Многомерное деление требует мономиального упорядочения, базис зависит от выбранного базисного упорядочения, и различные упорядочения приводят к радикально разным базисам Гребнера. Двумя наиболее часто используемыми порядками являются лексикографический порядок и обратный лексикографический порядок степеней (также называемый градуированным обратным лексикографическим порядком или просто полным порядком степеней). Лексикографический порядок исключает переменные, однако результирующие базы Грёбнера часто очень велики и дороги в вычислении. Обратный лексикографический порядок обеспечивает самые быстрые вычисления базиса Гребнера. В этом порядке мономы сначала сравниваются по общей степени, а связи разрываются путем взятия наименьшего монома относительно лексикографической упорядочения с измененными переменными.

В большинстве случаев (например, многочлены от конечного числа с комплексными коэффициентами или в более общем смысле, коэффициенты над любым полем), базисы Грёбнера существуют для любого мономиального порядка. Алгоритм Бухбергера - самый старый и самый известный метод их вычислений. Другие методы - это алгоритмы F4 и F5 Фогера, основанные на той же математике, что и алгоритм Бухбергера, и инволюционные подходы, основанные на идеях из дифференциальной алгебры. Также алгоритм три алгоритма преобразования базиса Грёбнера относительно одного мономиального порядка в базисе Грёбнера относительно другого мономиального порядка: алгоритм FGLM, алгоритм и. Эти алгоритмы часто используются для вычислений (сложных) лексикографических базисов Гребнера из (более простых)исов Гребнера полной степени.

Базис Грёбнера называется редуцированным, если старший коэффициент каждого элемента базиса равен 1 и ни один моном в любом элементе базиса не входит в идеал, порожденный старшими элементами других элементов базиса. В худшем случае для вычисления базиса Грёбнера может потребоваться время, которое является экспоненциальным или дважды экспоненциальным в количестве решений полиномиальной системы (для лексикографического порядка в обратном порядке и лексикографического порядка соответственно). Несмотря на стандартные, так и сокращенные базисы Гребнера часто вычислимы на практике, и большинство систем компьютерной алгебры содержат правила для этого.

Концепция и алгоритмы базисов Грёбнера были обобщены на подмодули из модулей модулей над кольцом полиномов. Фактически, если L - свободный модуль над кольцом R, то можно рассматривать R⊕L как кольцо, определив произведение двух элементов L равным 0. Это кольцо можно отождествить с $R [e 1,…, El] / ⟨{eiej | 1 ≤ я ≤ j ≤ l}⟩, {\ Displaystyle R [e_ {1}, \ ldots, e_ {l}] / \ left \ langle \ {e_ {i} e_ {j} | 1 \ Leq я \ Leq j \ leq l \} \ right \ rangle,}$ $R [e_1, \ ldots, e_l] / \ left \ langle \ {e_ie_j | 1 \ le i \ le j \ le l \} \ right \ rangle,$ где $e 1,…, el {\ displaystyle e_ {1}, \ ldots, e_ {l}}$ $e_1, \ ldots, e_l$ является базисом L. Это позволяет идентифицировать подмодуль L, порожденный $g 1,…, gk {\ displaystyle g_ {1}, \ ldots, g_ {k}}$ $g_1, \ ldots, g_k$ с идеалом из $R [e 1,…, el] {\ displaystyle R [e_ {1}, \ ldots, e_ {l}]}$ $R [e_1, \ ldots, e_l]$ сгенерировано $g 1,…, gk {\ displaystyle g_ {1}, \ ldots, g_ {k}}$ $g_1, \ ldots, g_k$ и продукты $eiej {\ displaystyle e_ {i} e_ {j}}$ $e_ie_j$ , $1 ≤ i ≤ j ≤ l {\ Стиль отображения 1 \ Leq я \ Leq j \ Leq l}$ $1 \ le i \ le j \ le l$ . Если R - кольцо многочленов, это сводит теорию и алгоритмы базисов Грёбнера модулей к теории и алгоритам базисов Грёбнера идеалов.

Концепция и алгоритмы базисов Грёбнера также были обобщены идеалы над различными кольцами, коммутаторами или такими как кольца полиномов над кольцами главных идеалов или алгебрами Вейля.

Пример и контрпример

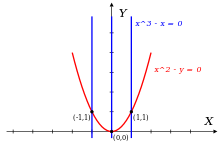Нули f (x, y) образуют красную параболу; нули g (x, y) образуют три синих вертикальных линий. Их пересечение состоит из трех точек.

Пусть R = Q [x, y] -кольцо двумерных многочленов с рациональными коэффициентами, и рассмотрим идеал I = , порожденный многочленами

f (x, y) = x - y

g (x, y) = x - x

Два других элемента являются многочленами

k (x, y) = -xf (x, y) + g (x, y) = xy - x

h (x, y) = xk (x, y) - (y - 1) f (x, y) = y - y

При лексикографическом порядке с x>y мы имеем

lt (f) = x

lt (g) = x

lt (h) = y

Идеал, порожденный {lt (f), lt (g)} содержит только многочлены, которые делятся на x, что исключает lt (h) = y; отсюда следует, что {f, g} не является базисом Грёбнера для I.

С другой стороны, мы можем показать, что {f, k, h} действительно является базисом Грёбнера для I.

Во-первых, f и g и, следовательно, также имеют h, k и все другие многочлены в идеале I следующие три общих нуля в плоскости (x, y), как показано на рисунке: {(1,1), (- 1,1), (0,0)}. Эти три точки не коллинеарны, поэтому я не содержит полиномов первой степени. Я также не могу содержать многочлены специальной формы

m (x, y) = cx + p (y)

, где c - ненулевое рациональное число, а p - многочлен только от переменных y; причина в том, что у такого м никогда не может быть двух разных нулей с одинаковым значением y (в данном случае точки (1,1) и (-1,1)).

Из вышеизложенного следует, что I, помимо нулевого многочлена, содержит только многочлены, старший член имеет степень больше или равную 2; поэтому их главные члены делятся по крайней мере на один из трех мономов

{x, xy, y} = {lt (f), lt (k), lt (h)}.

Это означает, что {f, k, h} является базисом Грёбнера для лексикографической упорядочения с x>y.

Свойства и приложения базисов Грёбнера

Если явно не указаны параметры, все следующие результаты верны для любого мономиального упорядочения (см. Определения различных порядков в этой статье.).

Распространенное заблуждение, что лексикографический порядок необходим для некоторых из этих результатов. Напротив, лексикографический порядок почти всегда труднее всего вычислить, и его использование делает непрактичные вычисления, которые просты с градуированным обратным лексикографическим порядком (grevlex) или, когда необходимо исключение, порядком исключения (lexdeg), который ограничивается grevlex для каждого блока изолированного.

Равенство идеалов

Приведенные базисы Грёбнера уникальны для любого данного идеала и любого мономиального порядка. Таким образом, два идеала равны тогда и только тогда, когда они имеют один и тот же (редуцированный) базис Гребнера (обычно программное обеспечение базиса Грёбнера всегда производит редуцированные базисы Гребнера).

Принадлежность и включение идеалов

редукция многочлена f базисом Грёбнера G идеала I дает 0 тогда и только тогда, когда f принадлежит I. Это позволяет проверить принадлежность элемента к идеалу. Другой метод состоит в проверке того, что базис Грёбнера G∪ {f} равенство G.

Проверить, порожден ли идеал I с помощью f 1,..., f k содержится в идеале J, достаточно проверить, что каждое f i принадлежит J. Можно также проверить равенство приведенных базисов Грёбнера в J и J∪ {f 1,..., f k }.

Решения системы алгебраических уравнений

Любой набор многочленов можно рассматривать как систему полиномиальных уравнений, приравнивая многочлены к нулю. Множество решений такой системы зависит только от сгенерированного идеала и, следовательно, не изменяется при замене данного порождающего набора базисом Гребнера при любом порядке сгенерированного идеала. Такое решение с координатами в алгебраически замкнутом поле, содержащем коэффициенты многочленов, называется нулем идеала. В обычном случае рациональных коэффициентов это алгебраически замкнутое поле выбирается в качестве комплексного поля.

Идеал не имеет никакого нуля (система уравнений несовместима ) тогда и только тогда, когда 1 принадлежит идеалу (это Nullstellensatz Гильберта), или, что то же самое, если его базис Грёбнера (для любого мономиального порядка) содержит 1, или, также, если соответствующий приведенный базис Грёбнера это [1].

Учитывая базис Грёбнера G идеала I, он имеет только конечное число нулей тогда и только тогда, когда для каждой переменной x G содержит многочлен со старшим мономом, являющимся степенью x ( без какой-либо другой переменной, появляющейся в ведущем члене). Если это так, то количество нулей, посчитанное с кратностью, равно количеству одночленов, не кратных старшему одночлену в G. Это число называется степенью идеала.

Когда количество нулей конечно, базис Грёбнера для лексикографического мономиального упорядочения теоретически обеспечивает решение: первые координаты решения являются корнем из наибольшего общего делителя числа полиномы базиса, зависящего только от первой переменной. После подстановки этого корня в базис вторыеТруды Американского математического общества 359 (2007), нет. 11, 5171–5192 (о бесконечномерных базисах Грёбнера для колец многочленов от бесконечного множества неопределенных).

Внешние ссылки

Собственная реализация Фогером его алгоритма F4
, Энциклопедия математики, EMS Press, 2001 [1994]
Б. Бухбергер, Основы Грёбнера: краткое введение для теоретиков систем в Труды EUROCAST 2001.
Бухбергер, Б. и Заплетал, А. Библиография баз Грёбнера.
Сравнительное время Страница программного обеспечения Gröbner Bases
Проф. Бруно Бухбергер Бруно Бухбергер
Вайсштейн, Эрик В. «Основа Грёбнера». MathWorld.
Введение в основы Грёбнера в Scholarpedia