Войти
регулярный семиугольник нельзя построить с использованием только линейки и компаса ; это может быть доказано с помощью поля конструктивных чисел.В математике поле представляет собой набор, на котором сложение, вычитание, умножение и деление и ведут себя как соответствующие операции с рациональными и действительными делай. Таким образом, поле представляет собой фундаментальную алгебраическую структуру, которая широко используется в алгебре, теории чисел и многих других областях математики.
Наиболее известными полями являются поле рациональных чисел, поле действующих чисел и поле комплексных чисел. Обычно используются многие другие поля, такие как поля рациональных функций, поля алгебраических функций, поля алгебраических чисел и p-адические поля. используется и изучается в математике, в частности в теории чисел и алгебраической геометрии. Большинство криптографических протоколов полагаются на конечные поля, т. Е. Поля с конечным числом элементов .
Связь двух полей выражается понятием расширения поля . Теория Галуа, начатая Эваристом Галуа в 1830-х годах, посвящена пониманию симметрии расширений поля. Среди других результатов эта теория показывает, что трисекция угла и квадратура круга могут быть выполнены с помощью циркуля и линейки. Более того, он показывает, что уравнения пятой степени алгебраически неразрешимы.
Поля земли основополагающими понятиями в нескольких математических областях. Сюда входят различные разделы математического анализа, которые основаны на полях с дополнительной структурой. Основные теоремы поля анализа зависят от структурных свойств чисел. Что обычно важно для алгебраических целей, любое поле может ввести в должность в скаляров для прост-пространстве, которое является стандартным общим контекстом для линейной алгебры. Числовые поля, родственники поля рациональных чисел, подробно изучаются в теории чисел. Функциональные поля могут помочь описать свойства геометрических объектов.
Неформально, поле - это набор вместе с двумя операциями , определенными для этого набора: операция сложения, записанная как a + b и операция умножения, записанная как a ⋅ b, обе из которых ведут себя так же, как и для рациональных чисел и действительных чисел, включая существование добавки обратный -a для всех элементы a и мультипликативный обратный b для каждого ненулевого элемента b. Это позволяет также использовать так называемые обратные операции вычитания, a - b и деления, a / b, путем определения:
Формальное поле - это набор F вместе с двумя бинарными операциями над F называются сложением и умножением. Бинарная операция на F - это отображение F × F → F, то есть соответствие, которое ставит в соответствие каждой упорядоченной паре элементов F однозначно определенный элемент F. Результат сложения a и b называется суммой a и b, и обозначается a + b. Точно так же результат умножения a и b называется произведением a и b и обозначается ab или a ⋅ b. Эти операции требуются для удовлетворения следующих свойств, называемых аксиомами поля . В этих аксиомах a, b и c - произвольные элементы поля F.
Это можно резюмировать, говоря: поле имеет две операции, называемое сложением и умножением; это абелева группа при добавлении с 0 в качестве аддитивной идентичности; ненулевые элементы являются абелевой группой относительно умножения на 1 как мультипликативную единицу; и умножение распределяется по сложению.
Поля также могут быть определены разными, но эквивалентными способами. В качестве альтернативы можно определить поле с помощью четырех бинарных операций (сложение, вычитание, умножение и деление) и их требуемых свойств. Деление на ноль по определению исключено. Чтобы избежать экзистенциальных кванторов, поля могут быть эффективными двумя бинарными операциями (сложными и умножением), двумя унарными операциями (дающими соответственно аддитивную и мультипликативную инверсию) и двумя нулевыми операциями (постоянные 0 и 1). Затем эти операции подлежат условиям, указанным выше. Избегать экзистенциальных кванторов важно в конструктивной математике и вычислениях. Эквивалентно можно определить поле с помощью тех же двух бинарных операций, одной унарной операции (мультипликативная обратная) и двух констант 1 и -1, поскольку 0 = 1 + (-1) и -a = (-1) a.
Рациональные числа широко использовались задолго до разработки концепции поля. Это числа, которые можно записать как дроби a / b, где a и b - целые числа, а b ≠ 0. Аддитивное обратное значение такого дроби равно −a / b, а мультипликативный обратный (при условии, что a ≠ 0) равенство b / a, что можно увидеть следующим образом:
Абстрактные требуемые аксиомы поля сводятся к стандартным свойствам рациональных чисел. Например, закон дистрибутивности может быть доказан следующим образом:
![{\ displaystyle {\ begin {align} {\ frac {a} {b}} \ cdot \ left ({\ frac {c} {d}} + {\ frac {e} {f}} \ right) \\ [6pt] = {} {\ frac {a} {b}} \ cdot \ left ({\ frac {c} {d}} \ cdot {\ frac {f} {f}} + {\ frac {e} {f}} \ cdot {\ frac {d} {d}} \ right) \\ [6pt] = {} {\ frac {a} {b }} \ cdot \ left ({\ frac {cf} {df}} + {\ frac {ed} {fd}} \ right) = {\ frac {a} {b}} \ cdot {\ frac {cf + ed} {df}} \\ [6pt] = {} {\ frac {a (cf + ed)} {bdf}} = {\ frac {acf} {bdf}} + {\ frac {aed} {bdf }} = {\ frac {ac} {bd}} + {\ frac {ae} {bf}} \\ [6pt] = {} {\ frac {a} {b}} \ cdot {\ frac {c } {d}} + {\ frac {a} {b}} \ cdot {\ frac {e} {f}}. \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fdb74d800a57e82a5c69ce90ed98ddd3e9ebe3bc)
Умножение комплексных чисел может быть геометрически визуализировано путем и масштабирования. вещественные числа Rс обычными операциями сложения и умножения также образуют поле. Комплексные числа Cсостоят из выражений
, где i - мнимая единица, т. Е. (Не действительное) число. такое, что i = −1. Сложение и умножение настоящих видов таким образом, чтобы выражения этого типа удовлетворяли всем аксиомам поля и, таким, выполнялись для C . Например, согласно закону распределения
Очевидно, что это снова появление числа выше типа, поэтому комплексные образуют поле. Комплексные числа могут быть геометрически представлены в виде точек на плоскости , с декартовыми координатами, заданными числами их описывающего выражения, или в виде стрелок от начала координат к этим точкам, заданным как их длина и угол, заключенный в определенном направлении. Сложение затем соответствует объединению стрелок в интуитивно понятный параллелограмм (добавление декартовых координат), а умножение - интуитивно не интуитивно - объединяет вращение и масштабирование стрелок (добавление углов и умножение длин). Поля действительных и комплексных чисел используются в математике, физике, технике, статистике и многих других научных дисциплинах.
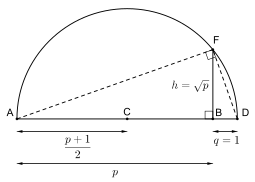теорема о среднем геометрическом утверждает, что h = pq. Выбор q = 1 позволяет построить квадратный корень из данного конструктивного числа p. В древности несколько геометрических проблем касались (не) возможности определенных чисел с помощью циркуля и линейки. Например, грекам было неизвестно, таким образом невозможно разделить заданный угол пополам. Эти проблемы могут быть решены с помощью поля конструктивных чисел. Действительные числа - это, по определению, длина отрезков линии, которые могут быть построены из точек 0 и 1 за конечное число шагов, используя только компас и линейку. Эти, наделенные полевыми операциями над действующими числами, ограниченными конструктивными числами, образуют поле, которое должным образом включает поле Q рациональных чисел. На иллюстрации показано построение квадратных корней из конструктивных чисел, не обязательно установленыся в Q . Используя обозначения на иллюстрации, постройте сегменты AB, BD и полукруг над AD (центр в средней точке C), который пересекает перпендикулярную линию. через B в точке F на расстоянии 
Не все действительные числа можно построить. Можно показать, что ![{\ displaystyle {\ sqrt [{ 3}] {2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710)
| Сложение | Умножение | ||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
В дополнение к знакомым системам счисления, такими как рациональные числа, есть другие, менее непосредственные примеры полей. Следующий пример представляет собой поле, состоящее из четырех элементов, называемых O, I, A и B. Обозначения выбраны так, что O играет роль аддитивного тождественного элемента (обозначенного 0 в аксиомах выше), а I - мультипликативное тождество. (обозначено 1 в аксиомах выше). Аксиомы поля могут быть проверены с помощью дополнительной теории поля или прямого вычисления. Например,
Это поле называется конечное поле с четырьмя элементами обозначается F4или GF (4). Подмножество, состоящее из O и I (выделено красным в таблицах справа), также является полем, известным как двоичное поле F2или GF (2). В контексте информатики и булевой алгебры, затем O и I часто обозначаются соответственно ложным и истинным, добавление обозначается XOR (исключающее или), а умножение обозначается И. Другими словами, структура двоичного поля является простой структурой, которая позволяет выполнять вычисления с битами.
В этом разделе F обозначает произвольное поле, а a и b произвольного поля элементы из F.
Один имеет · 0 = 0 и −a = (−1) · a. В частности, можно вывести аддитивное обратное для каждого элемента, как только известно –1.
Если ab = 0, то a или b должны быть 0, поскольку если a ≠ 0, то b = (aa) b = a (ab) = a⋅0 = 0. Это означает, что каждый поле является областью целостности.
Кроме того, для любых элементов a и b верны следующие свойства:
Из аксиом поля F следует, что это абелева группа при дополнение. Эта группа называется аддитивной группой поля и иногда обозначается (F, +), когда обозначение ее просто как F может осуществить в заблуждение.
Аналогичным образом ненулевые элементы F \ {0} или F.
образуют образ абелеву группу при умножении, называемую мультипликативной группой и обозначаемымТаким образом, поле может быть определено как множество F, снабженное двумя операциями, обозначенными как сложение и умножение, так что F - абелева группа при сложении, F \ {0} - абелева группа при умножении (где 0 - это тождественный элемент сложения), а умножение - это распределительное над сложением. Поэтому некоторые элементарные утверждения о полях можно получить, применяя общие факты о группах. Например, аддитивные и мультипликативные обратные -a и однозначно определяется a.
Требование 1 ≠ 0, потому что 1 - это единичный элемент группы, не содержащий 0. Таким образом, тривиальное кольцо, состоящее из одного элемента, не является полем.
Каждая конечная подгруппа мультипликативной группы поля является циклической (см. Корень единицы § Циклические группы ).
В дополнение к умножению двух элементов F можно определить произведение n ⋅ произвольного элемента a из F на положительное целое число n-кратной суммой
Если не существует такого положительного целого числа, то
, то говорят, что F имеет характеристику 0. Например, поле рациональных чисел Q имеет характеристику 0, поскольку ни одно положительное целое число не равно нулю. В противном случае, если существует положительное целое число, удовлетворяющее это уравнение, меньшее такое положительное целое число может быть показано как простое число. Обычно его обозначают p, и тогда говорят, что поле имеет свойство p. Например, поле F4имеет характеристику 2, поскольку (в обозначенной приведенной выше таблице приведенной выше) I + I = O.
Если F имеет характеристику p, то p ⋅ a = 0 для всех a в F. Это означает, что
, поскольку все другие биномиальные коэффициенты, встречающиеся в биномиальной формуле, дел на p. Здесь a: = a ⋅ a ⋅... ⋅ a (p факторов) - это p-я степень, то есть p-кратное произведение элемента a. Следовательно, отображается Фробениуса
совместимо со сложением в F (а также с умножением) и, следовательно, является гомоморфизмом полей. Существование этого гомоморфизма отличает характеристики от полей характеристики 0.
A подполе E поля F - это подмножество F, которое является полем с относительно полевых операций F. Эквивалентно E подмножеством F, которое содержит 1 и замкнуто относительно сложения, умножения, аддитивного обратного и мультипликативного обратного ненулевого элемента. Это означает, что 1 ∊ E, что для всех a, b ∊ E как a + b, так и a · b находятся в E, и что для всех a ≠ 0 в E оба –a и 1 / a находятся в E.
Гомоморфизмы полей - это отображение f: E → F между двумя полями, такие что f (e 1 + e 2) = f (e 1) + f (e 2), f (e 1e2) = f (e 1) f (e 2) и f ( 1 E) = 1 F, где e 1 и e 2 - произвольные элементы E. Все гомоморфизмы полей инъективны. Если f также сюръективен, это называется изоморфизмом (или поля E и F называются изоморфными).
Поле называется общий полем, если оно не имеет собственных (т. Е. Строго меньших) подполей. Любое поле F содержит простое поле. Если характеристика F - p (простое число), то простое поле изоморфно конечному полю Fp, введенному ниже. В противном случае простое поле изоморфно Q.
Конечные поля (также называемые полями Галуа) - это поле с конечным числом элементов, число которых также называется порядком поля. Приведенный выше вводный пример F4представляет собой поле с четырьмя элементами. Его подполе F2является наименьшим полем, поскольку по определению поле имеет как минимум два различных элемента 1 ≠ 0.
В модульной арифметике по модулю 12 9 + 4 = 1, поскольку 9 + 4 = 13 в Z, который делится на 12, оставляет остаток 1. Однако Z / 12 Z не является полем, поскольку 12 не является простым числом. Простейшие конечные поля с простым порядком, непосредственно доступны с помощью модульной арифметики. Для фиксированного положительного целого числа n арифметика "по модулю n" означает работу с числами
Сложение и умножение этого набора выполняется путем выполнения рассматриваемая операция в наборе Z целых чисел, деление на n и получение остатка в качестве результата. Эта конструкция дает поле точно, если n является простым числом. Например, взяв простое число n = 2, вы получите указанное выше поле F2. Для n = 4 и в более общем случае для любого составного числа (т. Е. Любого числа n, которое может быть выражено как произведение n = r⋅s двух строго меньших натуральных чисел), Z/nZне является field: произведение двух ненулевых элементов равно нулю, поскольку r⋅s = 0 в Z/nZ, что, как было объяснено в выше, не позволяет Z/nZбыть полем. Поле Z/pZс p элементами (p - простое число), построенное таким образом, обычно обозначается Fp.
. Каждое конечное поле F имеет q = p элементов, где p простое и n ≥ 1. Это утверждение верно, поскольку F может быть рассматривается как векторное пространство над своим простым полем. Размерность этого векторного пространства обязательно конечна, скажем n, что подразумевает утвержденное утверждение.
Поле с q = p элементами может быть построено как поле разделения многочлена
Такое поле расщепления является расширением Fp, в котором многочлен f имеет q нулей. Это означает, что f имеет как можно больше нулей, поскольку степень функции f равна q. Для q = 2 = 4 с помощью приведенной выше таблицы умножения можноПроверить от случая к случаю, что все четыре элемента F4удовлетворяют уравнение x = x, поэтому они являются нулями f. Напротив, в F2f имеет только два нуля (а именно 0 и 1), поэтому f не разбивается на линейные множители в этом меньшем поле. Развивая далее основные теоретико-полевые понятия, можно показать, что два конечных поля одного порядка изоморфны. Таким образом, принято говорить о конечном поле с q элементами, обозначаемым Fqили GF (q).
Исторически три алгебраических дисциплины приводят к полю концепции: вопрос о решении полиномиальных уравнений, теория алгебраических чисел и алгебраическая геометрия. Первый шаг к понятию поля был сделан в 1770 году Жозефом-Луи Лагранжем, который заметил, что перестановка нулей x 1, x 2, x 3 кубического многочлена в выражении
(где ω является третьим корнем из единицы ) дает только два значения. Таким образом, Лагранж концептуально объяснил классический метод решения Принцип дельцов Ферро и Франсуа Вьете, который заключается в сведении кубического уравнения для неизвестного x к квадратному уравнению для x. Вместе с аналогичным наблюдением для области 4, Лагранж, таким, связал то, что в конечном итоге стало концепцией полей и концепцией групп. Вандермонде, также в 1770 году, и в более полной мере. Карл Фридрих Гаусс в своей книге Disquisitiones Arithmeticae (1801) изучил уравнение
для простого числа p и, снова используя современный язык, циклический группа Галуа. Гаусс пришел к выводу, что правильный p-угольник может быть построен, если p = 2 + 1. Основываясь на работе Лагранжа, Паоло Руффини утверждал (1799), что уравнения пятой степени (полиномиальные уравнения степени 5) не могут быть решены алгебраически; однако его аргументы были ошибочными. Эти пробелы были заполнены Нильсом Хенриком Абелем в 1824 году. Эварист Галуа в 1832 году разработал необходимые и достаточные критерии алгебраической разрешимости полиномиального уравнения, тем самым фактически установив то, что известно. как теория Галуа сегодня. И Абель, и Галуа работали с тем, что сегодня называется полем алгебраических чисел, но не придумали ни явного понятия поля, ни группы.
В 1871 году Ричард Дедекинд ввел для множества действующих или комплексных чисел, закрываемых четырьмя арифметическими операциями, немецкое Кёрпер, что означает «тело" или "корпус" ( Английский термин «поле» был введен Муром (1893).
Под полем мы будем понимать любую бесконечную систему действительных или комплексных чисел, настолько замкнутую в себе и совершенствующую сложность, вычитание, умножение и
— Ричард Дедекинд, 1871В 1881 году Леопольд Кронекер определил то, что он назвал областью рациональности, то есть областью рационального дроби в современном понимании. Понятие Кронекера не охватывало всех алгебраических чисел (которое является полем в смысле Дедекинда), но, с другой стороны, было более абстрактным, чем понятие Дедекинда, в том, что оно не делало предположений о природе элементен тов поля. Кронекер абстрактно интерпретировал такое поле, как Q (π), как поле рациональных функций Q (X). До этих примеров трансцендентных чисел были известны с работы Джозефа Лиувилля в 1844 году до Чарльза Эрмита (1873 г.) и Фердинанда фон Линдеманна (1882 г.). доказал трансцендентность e и π соответственно.
Первое четкое определение абстрактного поля дано Вебер (1893 г.). В частности, понятие Генриха Мартина Вебера включало область Fp. Джузеппе Веронезе (1891) изучал область формальных степенных рядов, что привело Гензеля (1904) в введем поле p-адических числа. Стейниц (1910) синтезировал знания абстрактной теории поля, накопленные к настоящему времени. Он аксиоматически изучал свойства полей и определенные важные теоретико-полевые концепции. Большинство теорем, упомянутых в разделах Теория Галуа, Построение полей и Элементарные понятия, можно найти в работе Стейница. Artin Schreier (1927) связал понятие упорядочения в поле и, следовательно, область с чисто алгебраическими свойствами. Эмиль Артин заново разработал теорию Галуа. с 1928 по 1942 год, устранение зависимости от теоремы о примитивных элементах.
A коммутативное кольцо - это набор, оснащенный операциями сложения и умножения, удовлетворяющие всем аксиомам поля, за исключением использования мультипликативных обратных a. Например, целые числа Z образуют коммутативное кольцо, но не поле: обратная величина целого числа n сама по себе не является целым числом, если только n = ± 1.
Каждый ненулевой элемент является единичным элементом (что означает, что каждый элемент обратим). Точно так же поля - это коммутаторные кольца с ровно двумя различными идеалами, (0) и R. Поля также используются в коммутаторах, которые (0) является единственным простым идеалом.
Для коммутативного кольца R, есть два метода построить поле, связанное с R, т. е. два способа изменить R так, чтобы все ненулевые элементы стали обратимыми: формирование поля дробей и формирование полей вычетов. Поле дробей Z - это Q, рациональные числа, а поля вычетов Z - конечные поля Fp.
Для заданной области целостности R ее поле дробей Q (R) построено из дробей двух элементов R так же, как Q построено из целых чисел. Точнее, элементы Q (R) являются дроби a / b, где a и b лежат в R, а b ≠ 0. Две дроби a / b и c / d равны тогда и только тогда, когда ad = bc. Операция с дробями работает точно так же, как и с рациональными числами. Например,
Несложно показать, что если кольцо является областью целостности, множество дробей образуют поле.
Поле F (x) рациональных дробей над полем (или областью целостности) F является поле частных кольца многочленов F [x]. Поле F ((x)) из ряда Лорана
над полем F - это поле частных кольца F [[x]] из формальный степенной ряд (в котором k ≥ 0). Представление дробей в этой ситуации менее важно.
Помимо поля дробей, которое вводит R инъективно в поле, поле может быть получено из коммутативного кольца R с помощью сюръективное отображение на поле F. Любое поле, полученное таким образом, является частным R / m, где m - максимальный идеал поля R. Если R имеет только один максимальный идеал m, это поле называется полем вычетов Р.
Идеал , порожденный одним полиномом f в кольце многочленов R = E [X] (над полем E) является максимальным тогда и только тогда, когда f неприводимо в E, т. е. если f не может быть выражено как произведение двух многочленов от E [X] меньшей степени. Это дает поле
Это поле F содержит элемент x (а именно класс остатка X), который удовлетворяет уравнению
Например, C получается из Р посредством , примыкающего к символу мнимой единицы. i, что удовлетворяет f (i) = 0, где f (X) = X + 1. Более того, f неприводимо над R, откуда следует, что отображение, отправляющее многочлен f (X) ∊ R [X] в f (i) дает изоморфизм
![{\ displaystyle \ mathbf {R} [X] / \ left (X ^ {2} +1 \ right) \ {\ stackrel {\ cong} {\ longrightarrow}} \ \ mathbf {C}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca0f1bdfcfbc661e9a16477be8972a3bb7c281c5)
Поля могут быть созданы внутри данного большего контейнерного поля. Предположим, что дано поле E и поле F, содержащее E в качестве подполя. Для любого элемента x из F существует наименьшее подполе F, содержащее E и x, называемое подполем F, порожденное x и обозначаемое E (x). Переход от E к E (x) называется , соединяющим элемент с E. В более общем смысле, для подмножества S ⊂ F существует минимальное подполе F, содержащее E и S, обозначаемое E (S).
compositum из двух подполей E и E 'некоторого поля F наименьшим подполем F, содержащим как E, так и E'. Comositum может быть описанием самого большого подполя F, самого большого подполя F, языком алгебраического языка E.
Понятие подполя E ⊂ F также можно рассматривать с противоположной точки зрения, что F является расширением поля (или просто расширением) поля E, обозначаемым
и читать «F над E ».
Базовые новости расширения поля его степень [F: E], то есть размерность F как E-ограничения пространства. Он удовлетворяет формуле
Расширения, степень которых конечна, называются конечными расширениями. Расширения C/ Rи F4/ F2степень имеют 2, тогда как R/ Q- бесконечное расширение.
Ключевым понятием в расширении полей F / E являются алгебраические элементы. Элемент 
с e n,..., e 0 в E и e n ≠ 0. Например, мнимая единица i в C является алгебраической над R и даже над Q, поскольку она удовлетворяет уравнение
Расширение поля, в котором каждый элемент F является алгебраическим над E, называется алгебраическим расширением. Любое конечное расширение обязательно является алгебраическим, как можно вывести из приведенной выше формулы мультипликативности.
Подполе E (x), порожденное x, как указано выше, является алгебраическим расширением E тогда и только тогда, когда x равно алгебраический элемент. То есть, если x алгебраический, все остальные элементы E (x) также обязательно алгебраические. Более того, степень расширения E (x) / E, то есть размерность E (x) как E-векторного пространства, равна минимальной степени n, такой, что существует полиномиальное уравнение с участием x, как указано выше. Если эта степень равна n, то элементы E (x) имеют вид
Например, поле Q (i) из гауссовских рациональных чисел - это подполе C, состоящее из всех чисел формы a + bi, где и a, и b являются рациональными числами: слагаемые формы i (и аналогично для более высоких показателей) здесь не нужно учитывать, поскольку a + bi + ci можно упростить до a - c + bi.
Вышеупомянутое поле рациональных дробей E (X), где X является неопределенным, не является алгебраическим расширением элемента E, поскольку не существует полиномиального уравнения с коэффициентами в E, нуль которого равен X. Элементы, такие как X, которые не являются алгебраическими, называются трансцендентными. Неформально говоря, неопределенное X и его степени не взаимодействуют с элементами E. Аналогичное построение может быть выполнено с набором неопределенностей, а не только с одним.
Еще раз, расширение поля E (x) / E, рассмотренное выше, является ключевым примером: если x не является алгебраическим (т. Е. X не является корнем многочлена с коэффициентами в E), то E (x) изоморфно E (X). Этот изоморфизм получается заменой x на X в рациональных дробях.
Подмножество S поля F является базисом трансцендентности, если оно алгебраически независимое (не удовлетворяет никаким полиномиальным отношениям) над E и если F является алгебраическое расширение E (S). Любое расширение поля F / E имеет основу трансцендентности. Таким образом, расширения полей можно разделить на расширения вида E (S) / E (чисто трансцендентные расширения ) и алгебраические расширения.
Поле является алгебраически замкнутым, если оно не имеет строго больших алгебраических расширений или, что то же самое, при наличии полиномиального уравнения
имеет решение x ∊ F. По основной теореме алгебры, Cалгебраически замкнуто, т. е. любое полиномиальное уравнение с комплексными коэффициентами имеет комплексное решение. Рациональные и действительные числа не являются алгебраически замкнутыми, поскольку уравнение
не имеет рационального или действительного решения. Поле, содержащее F, называется алгебраическим замыканием поля F, если оно алгебраическое над F (грубо говоря, не слишком большое по сравнению с F) и алгебраически замкнуто (достаточно большое, чтобы содержать решения. всех полиномиальных уравнений).
Согласно вышеизложенному, C является алгебраическим замыканием R . Ситуация, когда алгебраическое замыкание является конечным расширением поля F, является совершенно особенным: по теореме Артина-Шрайера степень этого расширения обязательно равна 2, а F элементарно эквивалентен по R . Такие поля также известны как вещественные замкнутые поля.
Любое поле F имеет алгебраическое замыкание, которое, кроме того, уникально с точностью до (неединственного) изоморфизма. Обычно его называют алгебраическим замыканием и обозначают F. Например, алгебраическое замыкание Q элемента Q называется полем алгебраических чисел. Поле F обычно является скорее неявным, поскольку для его построения требуется лемма об ультрафильтре, теоретико-множественная аксиома, более слабая, чем аксиома выбора . В связи с этим алгебраическое закрытие Fqисключительно просто. Это объединение конечных полей, применение Fq(поля порядка q). Для любого алгебраически замкнутого поля F характеристики 0 алгебраическим замыканием поля F ((t)) ряда Лорана является поле ряда Пюизо, полученное соединение корней t.
Поля широко используются математике и за ее пределами, некоторые уточнения концепции были адаптированы к потребностям определенных математических областей.
Поле F называется упорядоченным полем, если можно сравнить любые два элемента, так что x + y ≥ 0 и xy ≥ 0, если x ≥ 0 и y ≥ 0., реалы образуют упорядоченное поле с обычным заказом ≥. Теорема Артина-Шрейера утверждает, что поле можно упорядочить тогда и только тогда, когда оно формально вещественным полем, что означает любое квадратное уравнение
имеет только решение x 1 = x 2 = ⋅⋅⋅ = x n = 0. Множество всех преступников порядков в фиксированном поле F изоморфно множеству кольцевые гомоморфизмы от кольца Витта W (F) квадратичных форм над F до Z.
Архимедово поле является упорядоченным таким полем, что для каждого элемента существует конечное выражение
, значение которого больше, чем у этого элемента, то есть бесконечных элементов нет. Эквивалентно поле не содержит бесконечно малых (элементы, меньшие, чем все рациональные числа); или, что эквивалентно, поле изоморфно подполю R.
Каждое ограниченное вещественное множество имеет меньшую верхнюю границу. Упорядоченное поле является полным по Дедекинду, если все верхние границы, нижние границы (см. дедекиндовский разрез ) и ограничения, которые должны существовать, действительно существуют. Более формально требуется, чтобы каждое ограниченное подмножество в F имело наименьшую верхнюю границу. Любое полное поле обязательно архимедово, поскольку в любом неархимедовом поле ни наивысшего бесконечно малого, ниеньшего положительного рационального числа, последовательность 1/2, 1/3, 1/4,..., каждый элемент которого больше, чем бесконечно малое не имеет предела.
Самостоятельно полным упорядоченным полем с точностью до изоморфизма, первый раз собственное подполе вещественных чисел содержит такие пробелы, R . Некоторые основополагающие результаты в исчислении непосредственно следуют из этих вещественных чисел.
гиперреалы Rобразуют упорядоченное поле, которое не является архимедовым. Это расширение вещественных чисел, полученное путем включения бесконечных и бесконечно малых чисел. Они больше или меньше любого действительного числа. Гиперреалы образуют фундаментальную основу нестандартного анализа.
Еще одно уточнение понятия поля - это топологическое поле, в котором множество F топологическое пространство, такое, что все операции над полем (сложение, умножение, отображение −a и a ↦ a) имеют непрерывными отображениями относительно топологии пространства. Топология всех полей, обсуждаемых ниже, вызвана метрикой , то есть функция
, которая измеряет расстояние между любыми двумя элементами F.
Завершение поля F - это еще одно поле, в котором, неформально говоря, заполняются «пробелы» в исходном поле F, если они есть. Например, любое иррациональное число x, такое как x = √2, является «пробелом» в рациональных числах Q в том смысле, что это действительное число, которое можно аппроксимировать произвольно. близко рациональными числами p / q, в том смысле, что расстояние x и p / q задано абсолютным значением | x - p / q | настолько мал, насколько желательно. В следующей таблице приведены некоторые примеры этой конструкции. Четвертый столбец показывает пример нулевой установить, то есть установить, предел определения (для n → ∞) равен нулю.
| Поле | Метрика | Завершение | нулевая последовательность |
|---|---|---|---|
| Q | | х - у | (обычное абсолютное значение ) | R | 1 / n |
| Q | , полученное с помощью p-адической оценки, для простого числа p | Qp(p-адических чисел ) | p |
| F (t). (F любое поле) | , полученное с использованием t-адической оценки | F ((t)) | t |
Поле Qpиспользуется в теории чисел, а p -адический анализ. Алгебраическое замыкание Qpнесет единственную норму, расширяющую норму, расширяющую норму на Qp, но не является полной. Cp.
Следующие топологические поля называются локальные поля :
Эти два типа локальных полей имеют неко торые фундаментальные общие черты., элементы p ∈ Qpи t ∈ Fp((t)) (называемые униформизатор ) соответствуют друг другу. Первое проявление этого находится на элементарном уровне: элементы обоих могут быть выражены в виде степенного ряда в униформизаторе с коэффициентами в Fp. (Однако, поскольку добавление в Qpвыполняется с использованием , несущего, что не относится к Fp((t), эти поля не изоморфны.) Следующие факты показывают что это поверхностное сходство идет намного глубже:
Дифференциальные поля - поля, снабженные производной, т. е. позволяют принимать производные от элементов в поле. Например, поле R (X) вместе со стандартной производной многочленов образует дифференциальное поле. Эти поля являются центральными дифференциальными уравнениями Галуа, вариант теории Галуа, имеющим дело с линейными дифференциальными уравнениями.
Теория Галуа изучает алгебраические расширения поля, изучая симметрию в арифметических операциях сложения и умножения. Важным понятием в этой области является понятие конечных расширений Галуа F / E, которые по определению являются разделяемыми и нормальными. Теорема о примитивном элементенте показывает, что конечные разделимые расширения обязательно простые, т. Е. Имеют форму
где f является неприводимым многочленом (как выше). Это означает, что все нули f в F и что f имеет только простые нули. Последнее условие всегда выполняется, если E имеет характеристику 0.
Для конечного расширения Галуа группа Галуа Gal (F / E) является группой полевых автоморфизмов из F, которые тривиальны на E (т. е. биекций σ: F → F, которые сохраняют сложение и умножение и отправляют элементы E в себя). Важность этой группы проистекает из фундаментальной теоремы теории Галуа, которая строит явное взаимно однозначное соответствие между набором подгрупп группы Gal (F / E) и множество промежуточных расширений расширений F / E. Посредством этого соответствия теоретико-групповые свойства превращаются в факты о полях. Например, если группа Галуа расширения Галуа, как указано выше, не разрешима (не может быть построена из абелевых групп ), то нули не могут быть выражены в терминах сложения, умножение и радикалы, т. е. выражения, ![{\ displaystyle {\ sqrt [{n}] {\}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eba618c922eacbc54a58e53b7a07be4cfd831221)
Тензорное произведение полей обычно является не полем. Например, конечное расширение тогда F / E степени n является расширением Галуа и только тогда, когда существует изоморфизм F-алгебр
Этот факт является началом из теории Галуа Гротендика, далеко идущего расширения теории Галуа, применимого к алгебро-геометрическим объектам.
Основные инварианты поля F включику и степень трансцендентности поля F над его простым полем. F, которые алгебраически замкнуты по совокупности. ля E и F являются изоляторными морфическими именно в том случае, если эти два совпадения совпадают. Это означает, что любые два несчетных алгебраически замкнутых поля одинаковой мощности и одинаковой характеристики изоморфны. Например, Qp, Cpи C изоморфны (но не изоморфны как топологические поля).
Принцип Лефшеца утверждает, что C элементарно эквивалентен любому алгебраически замкнутому полюсу F характеристики нуль. Более того, любое фиксированное утверждение φ выполняется в C тогда и только тогда, когда оно выполняется в любом алгебраически замкнутом поле достаточно высокой характеристики.
Если U является ультрафильтром на установить I, и F i является полем для каждого i в I, сверхпродукт из F i относительно U является полем. Он обозначается
, поскольку он ведет себя по-разному как предел полей F i: Теорема Лоса утверждает, что любое утверждение первого порядка, которое выполняется для всех, кроме конечного много F i, также справедливо для сверхпродукта. Применительно к предложенному выше предложению φ это показывает, что существует изоморфизм
Упомянутая выше теорема Акс-Кохена также следует из этого и изоморфизма ультрапроизведений (в обоих случаях по всем простым числам p)
Кроме того, теория моделей также имеет логические свойства различных типов полей, такие как вещественные закрытые поля или экспоненциальные поля (которые снабжены экспоненциальной функцией exp: F → F).
Для полей, которые не являются алгебраически замкнутыми (или несепарабельно замкнутыми), фундаментально важна абсолютная группа Галуа Gal (F): расширяя случай конечных расширений Галуа, описанный выше, эта группа управляет всеми конечными отделимыми расширениями F. Элементарными средствами можно показать, что группа Gal (Fq) группа Прюфера, проконечным пополнением группы Z . Это утверждение включает в себя тот факт, что единственными алгебраическими расширениями Gal (Fq) являются поля Gal (Fq) для n>0, и что группы Галуа этих конечных расширений задаются
Описание в терминах генераторов и отношений также известно для групп Галуа полей p-адических чисел (конечных расширений Qp).
представлений групп Галуа и связанных групп, таких как Группы Вейля являются фундаментальными во многих разделах арифметики Когомологическое исследование представлений проводится с использованием когомологий Галуа. Например, Группа Брауэра, которая классически определяется как группа центральных простых F -алгебр, может быть переинтерпретирована как группа когомологий Галуа, а именно
K-теория Милнора определяется как
теорема об изоморфизме вычетов по норме, доказанный около 2000 г. Владимиром Воеводским, связывает это с когомологией Галуа с помощью изоморфизма
Алгебраическая K-теория относится к группе обратимых матриц с коэффициентами данного поля. Например, процесс взятия определителя обратимой матрицы приводит к изоморфизму K 1 (F) = F. Теорема Мацумото показывает, что K 2 ( F) согласуется с K 2 (F). В более высоких степенях K-теория расходуется с K-теорией Милнора и остается сложной для вычислений в целом.
Углы Эйлера выражают отношение различных систем координат, то есть базисов R . Они используются в компьютерной графике. Если a ≠ 0, то уравнение
имеет единственное решение x в F, а именно x = b / a. Это наблюдение, используемым для демонстрации того, является важным ингредиентом, используемым для демонстрации того, что векторное пространство базис. Грубо говоря, это позволяет выбрать систему координат в любом векторном пространстве, что имеет центральное значение в линейной алгебре как с теоретической точки зрения, так и для практических приложений.
Модули (аналог векторных пространств) над большинством колец, включая кольцо Z целых чисел, имеют более сложную структуру. Конкретная ситуация, когда кольцо R является самостоятельным векторным пространством над полем F. Такие кольца называются F-алгебрами и подробно изучаются в области коммутативной алгебры. Например, нормализация Нётер утверждает, что любая конечно порожденная F-алгебра объединяет (точнее, конечно порождена как модуль над) кольцом многочленов F [x 1,..., x n].
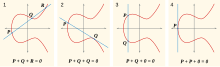Сумма трех точек P, Q и R на эллиптической кривой E (красная) равна нулю, если через эти точки проходит линия (синяя). Широко применяемая криптографическая процедура использует факт, что дискретное возведение в степень, т. е. вычисление
в (большом) конечном поле Fqможет быть выполнено намного эффективнее, чем дискретный логарифм, который является обратной операцией, т. е. решения n уравнения
В криптографии с эллиптической кривой умножение в конечном поле заменяется операцией сложения точек на эллиптической кривой, т. Е. Решений уравнения вида
Конечные поля также используются в теории кодирования и комбинаторике.
Компактная риманова поверхность рода два (два ручки). Род можно определить по полю мероморфных функций на поверхности. Функции в подходящем топологическом изображении X в поле могут быть добавлены и умножены поточечно, например, произведение двух функций произведено их значениями в пределах области:
Это делает эти функции k- коммутативными алгебрами.
, чтобы рассматривать алгебры функции, которые являются областями целостности. В этом случае отношения двух функций, т. Е. Выражения вида
сформировать поле, называемое полем функции.
Это происходит в двух основных случаях. Когда X является комплексным разнообразием X. В этом случае рассматривается алгебра голоморфных функций, т.е. комплексных дифференцируемых функций. Их отношения образуют поле мероморфных функций на X.
Функциональное поле алгебраического многообразия X (геометрический объект, определяемый как общие нули полиномиальных уравнений) состоит из отношений регулярных функций, т. е. отношений полиномиальных функций на множестве. Функциональное поле n-мерного пространства над полем k равно k (x 1,..., x n), то есть поле, состоящее из произведений многочленов от n неопределенностей. Функциональное поле X такое же, как поле любого открытого плотного подмногообразия. Другими словами, функциональное поле нечувствительно к замене X подмногообразием (немного) меньшего размера.
Функциональное поле инвариантно относительно изоморфизма и бирациональной эквивалентности разнообразий. Поэтому это важный инструмент для изучения абстрактных алгебраических многообразий и для классификации алгебраических многообразий. Например, измерение , которое равно степени трансцендентности k (X), инвариантно относительно бирациональной эквивалентности. Для кривых (т. Е. Размерность равна единице) поле функции k (X) очень близко к X: если X гладкий и правильный ( аналог компактности ), X может быть восстановлен с точностью до изоморфизма по его полю функций. В более высоком измерении функциональное поле запоминает меньше, но все же решающую информацию о X. Изучение функциональных полей и их геометрического значения в более высоких измерениях упоминается как бирациональная геометрия. Программа минимальных моделей пытается идентифицировать простейшие (в определенном точном смысле) алгебраические многообразия с заданным функциональным полем.
Глобальные поля находятся в центре внимания в теории алгебраических чисел и арифметической геометрии. Они, по определению, являются числовыми полями (конечные расширения Q ) или функциональными полями над Fq(конечные расширения Fq(t)). Что касается локальных полей, у этих двух типов полей есть несколько общих черт, хотя они имеют характеристику 0 и положительную характеристику соответственно. Эта аналогия функционального поля может помочь сформировать математические ожидания, часто сначала путем понимания вопросов о функциональных полях, а затем рассмотрения случая числового поля. Последнее часто бывает сложнее. Например, гипотеза Римана относительно нулей дзета-функции Римана (открыта с 2017 г.) может рассматриваться как параллельная гипотезе Вейля (доказана в 1974 году Пьером Делинем ).
Корни пятой степени из единицы образуют правильный пятиугольник.Циклотомические поля относятся к числу наиболее изученных числовых полей. Они имеют вид Q(ζn), где ζ n - примитивный n-й корень из единицы, т. Е. Комплексное число, удовлетворяющее ζ = 1 и ζ ≠ 1 для всех m < n. For n being a регулярное простое число, Куммер использовал циклотомические поля для доказательства последней теоремы Ферма, которая утверждает несуществование рациональных ненулевых решений уравнения
Локальные поля - это дополнения глобальных полей. Теорема Островского утверждает, что единственными дополнениями Q, глобального поля, являются локальные поля Qpи R . Изучение арифметических вопросов в глобальных полях может иногда выполняться, рассматривая соответствующие вопросы локально. Этот метод называется принцип локально-глобальный. Например, теорема Хассе – Минковского сводит проблему поиска рациональных решений квадратных уравнений к решению этих уравнений в R и Qp, решения которых легко описать.
В отличие от локальных полей, группы Галуа глобальных полей неизвестны. Обратная теория Галуа изучает (нерешенную) проблему, является ли какая-либо конечная группа группой Галуа Gal (F / Q ) для некоторого числового поля F. Теория поля классов описывает абелевы расширения, т. е. расширения с абелевой группой Галуа или, что то же самое, абелинизированные группы Галуа глобальных полей. Классическое утверждение, теорема Кронекера – Вебера, описывает максимальное абелево Q расширение Q : это поле
, полученный присоединением всех примитивных корней n-й степени из единицы. Jugendtraum Кронекера требует аналогичного явного описания F для общих числовых полей F. Для мнимых квадратичных полей, 
В дополнение к дополнительной структуре, которой могут обладать поля, поля допускают различные другие связанные понятия. Поскольку в любом поле 0 1, любое поле имеет не менее двух элементов. Тем не менее, существует концепция поля с одним элементом, которое предлагается как предел конечных полей Fp, так как p стремится к 1. Помимо телесных колец, существуют различные другие более слабые алгебраические структуры, относящиеся к полям, таким как квазиполя, ближние поля и полуполя.
Также существуют подходящие классы со структурой поля, которые иногда называется Поля с большой буквы. Сюрреалистические числа образуют Поле, содержащее действительные числа, и будут полем, за исключением того факта, что они являются правильным классом, а не набором. Нимберы, концепция из теории игр, также образуют такое Поле.
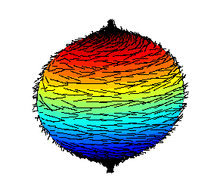Теорема о волосатом мяче гласит, что мяч нельзя расчесать. Более формально, нет непрерывного касательного векторного поля на сфере S, которое всюду не равно нулю. Отбросить одну или несколько аксиом в определение поля приводит к другим алгебраическим структурам. Как было сказано выше, коммутативные кольца удовлетворяют всем аксиомам полей, кроме мультипликативных обратных. Отказ от условия коммутативности умножения приводит к концепции делительного кольца или тела. Единственные тела, которые являются конечномерными пространствами векторов R, - это сам R, C (который является полем), кватернионы H(в которых умножение некоммутативно) и октонионы O(в которых умножение не коммутативно и не ассоциативно). Этот факт был доказан с использованием методов алгебраической топологии в 1958 году Мишелем Кервером, Раулем Боттом и Джоном Милнором. Отсутствие нечетномерной алгебры с делением является более классическим. Это можно вывести из теоремы о волосатом шарике, показанной справа.
 | В Wikibook абстрактной алгебре есть страница по теме: Fields |
