Российская кривая: коническое сечение
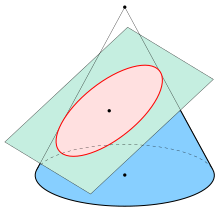
Эллипс (красный), полученный как пересечение конуса с наклонной плоскостью.

Эллипс: обозначения

Эллипсы: примеры с возрастающим эксцентриситетом
В математике, эллипс - это плоская кривая , окружающая два фокальные точки, так что для всех точек на кривой сумму двух расстояний до фокальных точек является постоянной. Таким образом, он обобщает круг , который представляет собой особый тип эллипса, в котором две точки фокусировки совпадают. Удлинение эллипса измеряется его эксцентриситетом e, числом от e = 0 (предельный случай окружности) до e = 1 (предельный случай бесконечного удлинения, больше не эллипс, а парабола ).
Эллипс имеет простое алгебраическое решение для своей площади, но только приближения для его периметра, для которого требуется интегрирование для получения точного решения.
Анали уравнение стандартного эллипса с центром в начале координат с шириной 2a и высотой 2b имеет вид:

Предполагая, что a ≥ b, фокусы равны (± c, 0) для  . Стандартное параметрическое уравнение:
. Стандартное параметрическое уравнение:

эллипсы являются закрытым типом конического сечения : плоская кривая, отслеживающая пересечение конуса с плоскостью (см. рисунок). Эллипсы имеют много общего с двумя другими формами конических сечений, параболами и гиперболами, обе из которых являются открытыми и неограниченными. Угловое поперечное сечение цилиндра также является эллипсом.
Эллипс также может быть определен в терминах одной точки фокусировки и линии за пределами эллипса, называемой направляющей : для всех точек на эллипсе отношение расстояния к фокус, расстояние до директрисы является постоянным. Это постоянное соотношение является упомянутым выше эксцентриситетом:
 .
.
Эллипсы распространены в физике, астрономии и инженерии. Например, орбита каждой планеты в солнечной системе представляет собой эллипс с Солнцем в одной точке фокусировки (точнее, фокус - это барицентр пары Солнце - планета). То же верно и для спутников, вращающихся вокруг планет, и для всех других систем двух астрономических тел. Формы планет и звезд часто хорошо описываются эллипсоидами. Круг, если смотреть под боковым углом, как эллипс: то есть эллипс - это изображение круга под параллельной или перспективной проекцией. Эллипс также является самой простой фигурой Лиссажу, образованной, когда горизонтальные и вертикальные движения синусоиды с одинаковой точностью: аналогичный эффект приводит к эллиптической поляризации света в оптика.
Имя λλειψις (élleipsis, «упущение») было дано Аполлонием Пергским в его Кониксах.
Содержание
- 1 Определение как геометрическое место точек
- 2 В декартовых координатах
- 2.1 Стандартное уравнение
- 2.2 Параметры
- 2.2.1 Главные оси
- 2.2.2 Линейный эксцентриситет
- 2.2.3 Эксцентриситет
- 2.2.4 Semi-latus rectum
- 2.3 Касательная
- 2.4 Сдвинутый эллипс
- 2.5 Общий эллипс
- 3 Параметрическое представление
- 3.1 Стандартное параметрическое представление
- 3.2 Рациональное представление
- 3.3 Наклон касательной как параметр
- 3.4 Общий эллипс
- 4 Полярные формы
- 4.1 Полярная форма относительно центра
- 4.2 Полярная форма относительно фокуса
- 5 Эксцентриситет и свойство директрисы
- 6 Свойство отражения от фокуса к фокусу
- 7 Сопряженные диаметры
- 7.1 Теорема Аполлония о сопряженных диаметрах
- 8 Ортогональные касательные
- 9 Рисование эллипсов
- 9.1 Построение точки де Ла Хира
- 9.2 Штифты Метод струн
- 9.3 Методы бумажной ленты
- 9.4 Аппроксимац ия соприкаса с кругами
- 9.5 Поколение Штейнера
- 9.6 Как гипотрохоида
- 10 вписанные углы и трехточечная форма
- 10.1 окружности
- 10.1.1 теорема вписанных углов для окружностей
- 10.1.2 трехточечная форма уравнения окружности
- 10.2 эллипсы
- 10.2.1 вписанные Теорема об углах для эллипсов
- 10.2.2 Трехточечная форма уравнения эллипса
- 11 Соотношение полюсов и полюсов
- 12 Метрические свойства
- 12.1 Площадь
- 12.2 Окружность
- 12.3 Кривизна
- 13 В геометрии треугольника
- 14 В виде плоских сечений квадрик
- 15 Приложения
- 15.1 Физика
- 15.1.1 Эллиптические отражатели и акустика
- 15.1.2 Планетарные орбиты
- 15.1.3 Гармонические осцилляторы
- 15.1.4 Просмотр фаз
- 15.1.5 Эллиптические шестерни
- 15.1.6 Оптика
- 15.2 Статистика и финансы
- 15.3 Компьютерная графика
- 15.4 Теория оптимизации
- 16 См. Также
- 17 Примечания
- 18 Ссылки
- 19 Внешние ссылки
Определение как геометрическое место точек
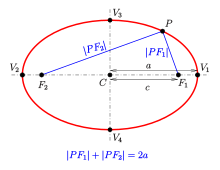
Эллипс: определение по сумме расстояний до фокусов
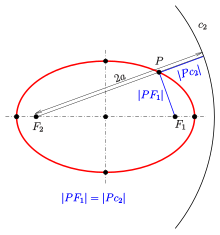
Эллипс: определение по фокусу и круговой направляющей
эллипс может быть определен геометрически как набор или геометрическое место точек на евклидовой плоскости:
- Даны две фиксированные точки
 называется фокусами и расстояние
называется фокусами и расстояние  , больше, чем расстояние между фокусами, эллипс - это набор точек
, больше, чем расстояние между фокусами, эллипс - это набор точек  такие, что сумма расстояний
такие, что сумма расстояний  равно
равно  :
:
Средняя точка  отрезка линии, соединяющего фокусы, называется центр эллипса. Линия, проходящая через фокус, называется большая осью, а линия, перпендикулярная ей, проходящая через центр, - малой осью. Большая ось пересекает эллипс в точках вершин
отрезка линии, соединяющего фокусы, называется центр эллипса. Линия, проходящая через фокус, называется большая осью, а линия, перпендикулярная ей, проходящая через центр, - малой осью. Большая ось пересекает эллипс в точках вершин  , которые имеют расстояние
, которые имеют расстояние  в центре. Расстояние
в центре. Расстояние  фокусов до центра называется фокусным расстоянием или линейным эксцентитетом. Частное
фокусов до центра называется фокусным расстоянием или линейным эксцентитетом. Частное  - это эксцентриситет.
- это эксцентриситет.
Случай  дает круг и включен как особый тип эллипса.
дает круг и включен как особый тип эллипса.
Уравнение  можно просмотреть по-другому (см. Рисунок):
можно просмотреть по-другому (см. Рисунок):
- If
 - круг со средней точкой
- круг со средней точкой  и радиусом
и радиусом  , тогда расстояние от точки
, тогда расстояние от точки  до окружности
до окружности  равно расстояние до фокуса
равно расстояние до фокуса  :
: 
 называется круговой направляющей (связано с фокусом
называется круговой направляющей (связано с фокусом  ) эллипса. Это свойство не следует путать с определением эллипса с помощью прямой линии ниже.
) эллипса. Это свойство не следует путать с определением эллипса с помощью прямой линии ниже.
Используя сферы Данделина, можно доказать, что любое плоское сечение конуса с плоскостью является эллипсом, при условии, что плоскость не содержит вершины и имеет наклон меньше, чем у прямого на конусе.
В декартовых координатах
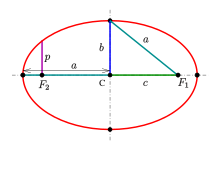
Параметры формы:
- a: большая полуось,
- b: малая полуось,
- c: линейный эксцентриситет,
- p: semi-latus rectum (обычно
 ).
).
Стандартное уравнение
Стандартная форма эллипса в декартовых координатах предполагает, что начало координат находится в центре эллипса ось x - большая ось, и:
- фокусы - это точка
 ,
, - вершинами являются
 .
.
для произвольной точки  расстояние до фокуса
расстояние до фокуса  равно
равно  и в другом фокусе
и в другом фокусе  . Следовательно, точка
. Следовательно, точка  находится на эллипсе всякий раз, когда:
находится на эллипсе всякий раз, когда:

Удаление радикалов подходящими квадратами и использованием  производит стандартное уравнение эллипса:
производит стандартное уравнение эллипса:

или, решенное относительно y:

Параметры ширины и высоты  называются большой и малой полуосями. Верхняя и нижняя точки
называются большой и малой полуосями. Верхняя и нижняя точки  - совпадающие вершины. Расстояния от точки
- совпадающие вершины. Расстояния от точки  на эллипсе до левого и правого фокусов равны
на эллипсе до левого и правого фокусов равны  и
и  .
.
Из уравнения следует, что эллипс симметричен относительно осей координат и, следовательно, относительно начала координат.
Параметры
Главные оси
В этой статье большая и малая полуоси обозначаются  и
и  соответственно, т.е.
соответственно, т.е. 
В принципе, каноническое уравнение эллипса  может иметь
может иметь
Линейный эксцентриситет
Это расстояние от центра к фокусу: c = a 2 - b 2 {\ displaystyle c = {\ sqrt {a ^ {2} -b ^ {2}}}} .
.
Эксцентриситет
Эксцентриситет можно выразить как:
- e = ca = 1 - (ba) 2 {\ displaystyle e = {\ frac {c} {a}} = {\ sqrt {1- \ left ({\ frac {b}) {a}} \ right) ^ {2}}}}
 ,
,
предположим г а>б. {\ displaystyle a>b.} Эллипс с одинаковыми осями (a = b {\ displaystyle a = b}
Эллипс с одинаковыми осями (a = b {\ displaystyle a = b} ) имеет нулевой эксцентриситет и представляет собой окружность.
) имеет нулевой эксцентриситет и представляет собой окружность.
-lat7
Длина хорды, проходящей через один очаг, перпендикулярной большой оси, называется latus rectum. Половина ее составляет semi-latus rectum ℓ {\ displaystyle \ ell} . Расчет показывает:
. Расчет показывает:
- ℓ знак равно b 2 a = a (1 - e 2). {\ Displaystyle \ ell = {\ frac {b ^ {2}} {a}} = a \ left (1-e ^ {2} \ right).}

Прямая полу-широта ℓ {\ displaystyle \ ell} равна радиусу кривизны в вершинах (см. Раздел кривизна).
равна радиусу кривизны в вершинах (см. Раздел кривизна).
Касательная
Произвольная линия g {\ displaystyle g} пересекает эллипс в 0, 1 или 2 точках соответственно называется внешней линией, касательной и с екущей. Через любую точку эллипса есть единственная касательная. Касательная в точке (x 1, y 1) {\ displaystyle (x_ {1}, \, y_ {1})}
пересекает эллипс в 0, 1 или 2 точках соответственно называется внешней линией, касательной и с екущей. Через любую точку эллипса есть единственная касательная. Касательная в точке (x 1, y 1) {\ displaystyle (x_ {1}, \, y_ {1})} эллипса x 2 a 2 + y 2 б 2 знак равно 1 {\ displaystyle {\ tfrac {x ^ {2}} {a ^ {2}}} + {\ tfrac {y ^ {2}} {b ^ {2}}} = 1}
эллипса x 2 a 2 + y 2 б 2 знак равно 1 {\ displaystyle {\ tfrac {x ^ {2}} {a ^ {2}}} + {\ tfrac {y ^ {2}} {b ^ {2}}} = 1} имеет координатное уравнение:
имеет координатное уравнение:
- x 1 a 2 x + y 1 b 2 y = 1. {\ displaystyle {\ frac {x_ {1}} {a ^ {2}}} x + {\ frac {y_ { 1}} {b ^ {2}}} y = 1.}

Векторное параметрическое уравнение касательной:
- x → = (x 1 y 1) + s (- y 1 a 2 Икс 1 б 2) {\ Displaystyle {\ vec {x}} = {\ begin {pmatrix} x_ {1} \\ y_ {1} \ end {pmatrix}} + s {\ begin {pmatrix} \; \! - y_ {1} a ^ {2} \\\; \ \ \ x_ {1} b ^ {2} \ end {pmatrix}} \}
 с s ∈ R. {\ displaystyle \ s \ in \ mathbb {R} \.}
с s ∈ R. {\ displaystyle \ s \ in \ mathbb {R} \.}
Доказательство: Пусть (x 1, y 1) {\ displaystyle (x_ {1}, \, y_ {1})} быть точкой на эллипсе и x → = (Икс 1 Y 1) + s (УФ) {\ textstyle {\ vec {x}} = {\ begin {pmatrix} x_ {1} \\ y_ {1} \ end {pmatrix}} + s {\ begin {pmatrix} u \\ v \ end {pmatrix}}}
быть точкой на эллипсе и x → = (Икс 1 Y 1) + s (УФ) {\ textstyle {\ vec {x}} = {\ begin {pmatrix} x_ {1} \\ y_ {1} \ end {pmatrix}} + s {\ begin {pmatrix} u \\ v \ end {pmatrix}}} быть уравнением любого прямого g {\ displaystyle g}
быть уравнением любого прямого g {\ displaystyle g} представ (x 1, y 1) {\ Displaystyle (x_ {1}, \, y_ {1})}
представ (x 1, y 1) {\ Displaystyle (x_ {1}, \, y_ {1})} . Вставка уравнения линии в уравнении эллипса и соблюдение x 1 2 a 2 + y 1 2 b 2 = 1 {\ displaystyle {\ frac {x_ {1} ^ {2}} {a ^ {2}}} + { \ frac {y_ {1} ^ {2}} {b ^ {2}}} = 1}
. Вставка уравнения линии в уравнении эллипса и соблюдение x 1 2 a 2 + y 1 2 b 2 = 1 {\ displaystyle {\ frac {x_ {1} ^ {2}} {a ^ {2}}} + { \ frac {y_ {1} ^ {2}} {b ^ {2}}} = 1} дает:
дает:
- (x 1 + su) 2 a 2 + (y 1 + sv) 2 b 2 знак равно 1 ⟹ 2 s (x 1 ua 2 + y 1 vb 2) + s 2 (u 2 a 2 + v 2 b 2) = 0. {\ displaystyle {\ frac {\ left (x_ {1) } + su \ right) ^ {2}} {a ^ {2}}} + {\ frac {\ left (y_ {1} + sv \ right) ^ {2}} {b ^ {2}}} = 1 \ \ quad \ Longrightarrow \ quad 2s \ left ({\ frac {x_ {1} u} {a ^ {2}}} + {\ frac {y_ {1} v} {b ^ {2}}} \ вправо) + s ^ {2} \ left ({\ frac {u ^ {2}} {a ^ {2}}} + {\ frac {v ^ {2}} {b ^ {2}}} \ right) = 0 \.}

- Тогда есть случаи:
- x 1 a 2 u + y 1 b 2 v = 0. {\ displaystyle {\ frac {x_ {1}} {a ^ {2}}} u + {\ frac {y_ {1}} {b ^ {2}}} v = 0.}
 Затем строка g {\ displaystyle g}
Затем строка g {\ displaystyle g} и эллипс имеют только точка (x 1, y 1) {\ displaystyle (x_ {1}, \, y_ {1})}
и эллипс имеют только точка (x 1, y 1) {\ displaystyle (x_ {1}, \, y_ {1})} в общем, а g {\ displaystyle g}
в общем, а g {\ displaystyle g} - ка сательная. Касательное направление имеет перпендикулярный вектор (x 1 a 2 y 1 b 2) {\ displaystyle {\ begin {pmatrix} {\ frac {x_ {1}} {a ^ {2}}} {\ frac {y_ {1}} {b ^ {2}}} \ end {pmatrix}}}
- ка сательная. Касательное направление имеет перпендикулярный вектор (x 1 a 2 y 1 b 2) {\ displaystyle {\ begin {pmatrix} {\ frac {x_ {1}} {a ^ {2}}} {\ frac {y_ {1}} {b ^ {2}}} \ end {pmatrix}}} , поэтому касательная линия имеет уравнение x 1 a 2 x + y 1 б 2 y = к {\ textstyle {\ frac {x_ {1}} {a ^ {2}}} x + {\ tfrac {y_ {1}} {b ^ {2}}} y = k}
, поэтому касательная линия имеет уравнение x 1 a 2 x + y 1 б 2 y = к {\ textstyle {\ frac {x_ {1}} {a ^ {2}}} x + {\ tfrac {y_ {1}} {b ^ {2}}} y = k} для некоторых k {\ displaystyle k}
для некоторых k {\ displaystyle k} . <Времен738>(x 1, y 1) {\ displaystyle (x_ {1}, \, y_ {1})}
. <Времен738>(x 1, y 1) {\ displaystyle (x_ {1}, \, y_ {1})} находится на касательной и эллипсе, получаем k = 1 {\ displaystyle к = 1}
находится на касательной и эллипсе, получаем k = 1 {\ displaystyle к = 1} .
. - x 1 a 2 u + y 1 b 2 v ≠ 0. {\ displaystyle {\ frac {x_ {1}} {a ^ {2}}} u + {\ frac {y_ {1) }} {b ^ {2}}} v \ neq 0.}
 Тогда строка g {\ displaystyle g}
Тогда строка g {\ displaystyle g} имеет вторую точку, общую с эллипсом, и является секансом.
имеет вторую точку, общую с эллипсом, и является секансом.
Используя (1), получаем, что (- y 1 a 2 x 1 b 2) {\ displaystyle {\ begin {pmatrix} -y_ {1} a ^ {2} x_ {1} b ^ {2} \ end {pmatrix}}} - касательный вектор в точке (x 1, y 1) {\ displaystyle (x_ {1}, \, y_ {1})}
- касательный вектор в точке (x 1, y 1) {\ displaystyle (x_ {1}, \, y_ {1})} , что доказывает образец уравнение.
, что доказывает образец уравнение.
Если (x 1, y 1) {\ displaystyle (x_ {1}, y_ {1})} и (u, v) {\ displaystyle (u, v)}
и (u, v) {\ displaystyle (u, v)} - две точки эллипса, такие что x 1 ua 2 + y 1 vb 2 = 0 {\ textstyle {\ frac {x_ {1} u} {a ^ { 2}}} + {\ tfrac {y_ {1} v} {b ^ {2}}} = 0}
- две точки эллипса, такие что x 1 ua 2 + y 1 vb 2 = 0 {\ textstyle {\ frac {x_ {1} u} {a ^ { 2}}} + {\ tfrac {y_ {1} v} {b ^ {2}}} = 0} , то точки лежат на двух сопряженных диаметрах (см. ниже). (Если a = b {\ displaystyle a = b}
, то точки лежат на двух сопряженных диаметрах (см. ниже). (Если a = b {\ displaystyle a = b} , эллипс представляет собой круг, а «сопряженный» означает «ортогональный».)
, эллипс представляет собой круг, а «сопряженный» означает «ортогональный».)
Сдвинутый эллипс
Если стандартный эллипс смещен так, чтобы его центр был (x ∘, y ∘) {\ displaystyle \ left (x _ {\ circ}, \, y _ {\ circ} \ right)} , его уравнение:
, его уравнение:
- (x - x ∘) 2 a 2 + (y - y ∘) 2 b 2 = 1. {\ displaystyle {\ frac {\ left (xx _ {\ circ} \ right) ^ {2}} {a ^ {2}}} + {\ frac {\ left (yy _ {\ circ} \ right)) ^ {2}} {b ^ {2}}} = 1 \.}

Оси по-прежнему параллельны осям x и y.
Общий эллипс
В аналитической геометрии эллипс определяется как квадрика: набор точек (X, Y) {\ displaystyle (X, \, Y)} в декартовой плоскости, которая в невырожденных случаях удовлетворяет неявному уравнению
в декартовой плоскости, которая в невырожденных случаях удовлетворяет неявному уравнению
- AX 2 + BXY + CY 2 + DX + EY + F = 0 {\ displaystyle AX ^ {2} + BXY + CY ^ {2} + DX + EY + F = 0}

при условии B 2–4 AC < 0. {\displaystyle B^{2}-4AC<0.}
Чтобы различать вырожденные случаи из невырожденного случая, пусть ∆ - детерминант
- ∆ = | A 1 2 B 1 2 D 1 2 B C 1 2 E 1 2 D 1 2 E F | = (AC - B 2 4) F + BED 4 - CD 2 4 - AE 2 4. {\ displaystyle \ Delta = {\ begin {vmatrix} A {\ frac {1} {2}} B {\ frac {1} {2}} D \\ {\ frac {1} {2}} BC и {\ frac {1} {2}} E \\ {\ frac {1} {2}} D {\ frac {1} {2}} EF \ end {vmatrix}} = \ left (AC - {\ frac {B ^ {2}} {4}} \ right) F + {\ frac {BED} {4}} - {\ frac {CD ^ {2}} {4}} - {\ frac {AE ^ {2}} {4}}.}

Тогда эллипс является невырожденным действительным эллипсом тогда и только тогда, когда C∆ < 0. If C∆>0, у нас есть мнимый эллипс, а если ∆ = 0, у нас есть точечный эллипс.
коэффициенты общих уравнений могут быть получены из известной большой полуоси a {\ displaystyle a} , малой полуоси b {\ displaystyle b}
, малой полуоси b {\ displaystyle b} , координаты центра (x ∘, y ∘) {\ displaystyle \ left (x _ {\ circ}, \, y _ {\ circ} \ right)}
, координаты центра (x ∘, y ∘) {\ displaystyle \ left (x _ {\ circ}, \, y _ {\ circ} \ right)} и угол поворота θ {\ displaystyle \ theta}
и угол поворота θ {\ displaystyle \ theta} (угол между положительной горизонтальной осью и большой осью эллипса) по формулам:
(угол между положительной горизонтальной осью и большой осью эллипса) по формулам:
- A = a 2 sin 2 θ + b 2 cos 2 θ B = 2 (b 2 - a 2) sin θ cos θ C = a 2 cos 2 θ + b 2 sin 2 θ D = - 2 A x ∘ - B y ∘ E = - B x ∘ - 2 C у ∘ F = A Икс ∘ 2 + В Икс ∘ Y ∘ + С Y ∘ 2 - а 2 б 2. {\ Displaystyle {\ begin {align} A = a ^ {2} \ sin ^ {2} \ theta + b ^ {2 } \ cos ^ {2} \ theta \\ B = 2 \ left (b ^ {2} -a ^ {2} \ right) \ sin \ theta \ cos \ theta \\ C = a ^ {2} \ cos ^ {2} \ theta + b ^ {2} \ sin ^ {2} \ theta \ \ D = - 2Ax _ {\ circ} -By _ {\ circ} \\ E = - Bx _ { \ circ} -2Cy _ {\ circ} \\ F = Ax _ {\ circ} ^ {2} + Bx _ {\ circ} y _ {\ circ} + Cy _ {\ circ} ^ {2} -a ^ {2} b ^ {2}. \ end {align}}}

Эти выражения могут быть получены из канонического уравнения x 2 a 2 + y 2 b 2 = 1 {\ displaystyle {\ tfrac {x ^ {2}} {a ^ {2 }}} + {\ tfrac {y ^ {2}} {b ^ {2}}} = 1} аффинным преобразованием координат (x, y) {\ displaystyle (x, \, y)}
аффинным преобразованием координат (x, y) {\ displaystyle (x, \, y)} :
:
- x = (X - x ∘) cos θ + (Y - y ∘) sin θ y = - (X - x ∘) sin θ + (Y - y ∘) cos θ. {\ Displaystyle {\ begin {выровнено} х = \ влево (X-х _ {\ circ} \ right) \ cos \ theta + \ left (Yy _ {\ circ} \ right) \ sin \ theta \\ y = - \ left (Xx _ {\ circ} \ right) \ sin \ theta + \ left (Yy _ {\ circ} \ right) \ cos \ theta. \ end {align}}}

И наоборот, Параметры канонической формы могут быть получены из коэффициентов общей формы с помощью уравнений:
- a, b = - 2 (AE2 + CD 2 - BDE + (B 2 - 4 AC) F) ((A + C) ± (A - C) 2 + B 2) B 2 - 4 AC x ∘ = 2 CD - BEB 2 - 4 AC y ∘ = 2 AE - BDB 2 - 4 AC θ = {arctan (1 B (C - A - (A - C) 2 + B 2)) для B ≠ 0 0 для B = 0, A < C 90 ∘ for B = 0, A>C { \ displaystyle {\ begin {align} a, b = {\ frac {- {\ sqrt {2 {\ \ Big (} AE ^ {2} + CD ^ {2} -BDE + (B ^ {2} - 4AC) F {\ Big)} \ left ((A + C) \ pm {\ sqrt {(AC) ^ {2} + B ^ {2}}} \ right)}}} {B ^ {2} - 4AC}} \\ x _ {\ circ} = {\ frac {2CD-BE} {B ^ {2} - 4AC}} \\ [3pt] y _ {\ circ} = {\ frac {2AE- BD} {B ^ {2} -4AC}} \\ [3pt] \ theta = {\ begin {cases} \ arctan \ left ({\ frac {1} {B}} \ left (CA - {\ sqrt {(AC) ^ {2} + B ^ {2}}} \ right) \ right) {\ text {for}} B \ neq 0 \\ 0 {\ text {for}} B = 0, \ A C \\\ end {case}} \ end {align}}}
![{\displaystyle {\begin{aligned}a,b={\frac {-{\sqrt {2{\Big (}AE^{2}+CD^{2}-BDE+(B^{2}-4AC)F{\Big)}\left((A+C)\pm {\sqrt {(A-C)^{2}+B^{2}}}\right)}}}{B^{2}-4AC}}\\x_{\circ }={\frac {2CD-BE}{B^{2}-4AC}}\\[3pt]y_{\circ }={\frac {2AE-BD}{B^{2}-4AC}}\\[3pt]\theta ={\begin{cases}\arctan \left({\frac {1}{B}}\left(C-A-{\sqrt {(A-C)^{2}+B^{2}}}\right)\right){\text{for }}B\neq 0\\0{\text{for }}B=0,\ A<C\\90^{\circ }{\text{for }}B=0,\ A>C \\\ end {case}} \ end {align}}}]( https: //wikimedia.org/api/rest_v1/media/math/render/svg/acde65bb036f1c47ad935258399a696f50875a68)
Параметрическое представление
П остроение точек связано на основе параметрического уравнения и интерпретации t, что с de la Hire

Точки Эллипса, вычисленные с помощью рационального представления с равными разнесенными объектами (
Δ u = 0,2 {\ displaystyle \ Delta u = 0, 2}
).
Стандартное параметрическое представление
Использование тригонометрические функции, параметрическое представление стандартного эллипса x 2 a 2 + y 2 b 2 = 1 {\ displaystyle {\ tfrac {x ^ {2}} {a ^ {2}}} + {\ tfrac {y ^ {2}} {b ^ {2}}} = 1} равно:
равно:
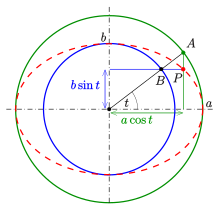
- (x, y) = (a cos t, b sin t), 0 ≤ t < 2 π. {\displaystyle (x,\,y)=(a\cos t,\,b\sin t),\ 0\leq t<2\pi \.}

Параметр t (который в астрономии называется эксцентрической аномалией ) не является углом (x (t), y ( t)) {\ displaystyle (x (t), y (t))} с осью x, но имеет геометрию этрическое значение согласно Philippe de L Прокат (см. Рисование эллипсов ниже).
с осью x, но имеет геометрию этрическое значение согласно Philippe de L Прокат (см. Рисование эллипсов ниже).
Рациональное представление
С заменой u = tan (t 2) {\ textstyle u = \ tan \ left ({\ frac {t} {2}} \ right) } и тригонометрические формулы
и тригонометрические формулы
- cos t = 1 - u 2 U 2 + 1, T знак равно 2 uu 2 + 1 {\ displaystyle \ cos t = {\ frac {1- u ^ {2}} {u ^ {2} +1}} \, \ quad \ sin t = {\ frac {2u} {u ^ {2} +1}}}

и рациональное параметрическое уравнение эллипса
- x (u) = a 1 - u 2 u 2 + 1 y (u) = 2 buu 2 + 1, - ∞ < u < ∞, {\displaystyle {\begin{aligned}x(u)=a{\frac {1-u^{2}}{u^{2}+1}}\\y(u)={\frac {2bu}{u^{2}+1}}\end{aligned}}\;,\quad -\infty

который покрывает любую точку эллипса x 2 a 2 + y 2 b 2 = 1 {\ displaystyle {\ tfrac {x ^ {2}} {a ^ {2}}} + {\ tfrac {y ^ {2}} {b ^ {2}}} = 1} кроме вершины левой (- a, 0) {\ displaystyle (-a, \, 0)}
кроме вершины левой (- a, 0) {\ displaystyle (-a, \, 0)} .
.
Для u ∈ [0, 1], {\ displaystyle u \ in [0, \, 1 ],}![{\displaystyle u\in [0,\,1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c61b780db9ac550dd283876e16abe9c2cccdf8c3) эта формула представляет правый верхний четверть эллипса, движущегося против часовой стрелки u. {\ displaystyle u.}
эта формула представляет правый верхний четверть эллипса, движущегося против часовой стрелки u. {\ displaystyle u.} Левая вершина является пределом lim u → ± ∞ (x (u), y (u)) = (- a, 0). {\ displaystyle \ lim _ {u \ to \ pm \ infty} (x (u), \, y (u)) = (- a, \, 0) \;.}
Левая вершина является пределом lim u → ± ∞ (x (u), y (u)) = (- a, 0). {\ displaystyle \ lim _ {u \ to \ pm \ infty} (x (u), \, y (u)) = (- a, \, 0) \;.}
Рациональные представления конических сечений обычно используются в автоматизированном проектировании (см. кривая Безье ).
Наклон касательной как параметр
Параметрическое представление, в котором используется наклон m {\ displaystyle m} касательной в точке эллипса, можно полученное из производной стандартного представления Икс → (T) = (a соз T, b sin t) T {\ displaystyle {\ vec {x}} (t) = (a \ cos t, \, b \ sin t) ^ {\ mathsf {T}}}
касательной в точке эллипса, можно полученное из производной стандартного представления Икс → (T) = (a соз T, b sin t) T {\ displaystyle {\ vec {x}} (t) = (a \ cos t, \, b \ sin t) ^ {\ mathsf {T}}} :
:
- x → ′ (t) = (- грех t, b cos t) T → m = - ba cot t → cot t = - маб. {\ displaystyle {\ vec {x}} '(t) = (- a \ sin t, \, b \ cos t) ^ {\ mathsf {T}} \ quad \ rightarrow \ quad m = - {\ frac { b} {a}} \ cot t \ quad \ rightarrow \ quad \ cot t = - {\ frac {ma} {b}}.}

С помощью тригонометрических формул получаем:
- cos t = детская кроватка t ± 1 + детская кроватка 2 t = - ma ± m 2 a 2 + b 2, sin t = 1 ± 1 + детская кроватка 2 t = b ± m 2 a 2 + b 2. {\ displaystyle \ cos t = {\ frac {\ cot t} {\ pm {\ sqrt {1+ \ cot ^ {2} t}}}} = {\ frac {-ma} {\ pm {\ sqrt { m ^ {2} a ^ {2} + b ^ {2}}}} \, \ quad \ quad \ sin t = {\ frac {1} {\ pm {\ sqrt {1+ \ cot ^ {2) } t}}}} = {\ frac {b} {\ pm {\ sqrt {m ^ {2} a ^ {2} + b ^ {2}}}}}.}

Замена cos t {\ displaystyle \ cos t} и sin t {\ displaystyle \ sin t}
и sin t {\ displaystyle \ sin t} стандартного представления дает:
стандартного представления дает:
- c → ± (m) = ( - ma 2 ± m 2 a 2 + b 2, b 2 ± m 2 a 2 + b 2), m ∈ R. {\ displaystyle {\ vec {c}} _ {\ pm} (m) = \ left ( - {\ frac {ma ^ {2}} {\ pm {\ sqrt {m ^ {2} a ^ {2}) + b ^ {2}}}}}, \; {\ frac {b ^ {2}} {\ pm {\ sqrt {m ^ {2} a ^ {2} + b ^ {2}}}} \ right), \, m \ in \ mathbb {R }.}

Здесь m {\ displaystyle m} - наклон касательной в точке эллипса, c → + {\ displaystyle {\ vec {c}} _ {+} }
- наклон касательной в точке эллипса, c → + {\ displaystyle {\ vec {c}} _ {+} } является верхним, а c → - {\ displaystyle {\ vec {c}} _ {-}}
является верхним, а c → - {\ displaystyle {\ vec {c}} _ {-}} нижняя половина эллипса. Вершины (± a, 0) {\ displaystyle (\ pm a, \, 0)}
нижняя половина эллипса. Вершины (± a, 0) {\ displaystyle (\ pm a, \, 0)} , имеющие вертикальные касательные, не охватываются представлением.
, имеющие вертикальные касательные, не охватываются представлением.
Уравнение касательной в точке c → ± (m) {\ displaystyle {\ vec {c}} _ {\ pm} (m)} имеет вид y знак равно mx + n {\ displaystyle y = mx + n}
имеет вид y знак равно mx + n {\ displaystyle y = mx + n} . Все еще неизвестное n {\ displaystyle n}
. Все еще неизвестное n {\ displaystyle n} может быть определено вставки координат точки эллипса c → ± (m) {\ displaystyle {\ vec {c}} _ {\ pm } (m)}
может быть определено вставки координат точки эллипса c → ± (m) {\ displaystyle {\ vec {c}} _ {\ pm } (m)} :
:
- y = mx ± m 2 a 2 + b 2. {\ displaystyle y = mx \ pm {\ sqrt {m ^ {2} a ^ {2} + b ^ {2}}} \;.}

Это описание касательных эллипса является важным инструментом для определения ортоптики эллипса. Ортоптическая статья содержит другое доказательство, без дифференциального исчисления и тригонометрических формул.
Общий эллипс

Эллипс как аффинное изображение единичной окружности
Другое определение эллипса использует аффинные преобразования :
- Любой эллипс является аффинным представлением единичной окружности с уравнением x 2 + y 2 = 1 {\ displaystyle x ^ {2} + y ^ {2} = 1}
 .
.
- параметрическое представление
Аффинное преобразование евклидовой плоскости вид x → ↦ е → 0 + A x → {\ displaystyle {\ vec {x}} \ mapsto {\ vec {f}} \! _ {0} + A {\ vec {x}}} , где A {\ displaystyle A}
, где A {\ displaystyle A} - это обычная матрица (с ненулевым определителем ) и f → 0 {\ displaystyle {\ vec {f}} \! _ {0}}
- это обычная матрица (с ненулевым определителем ) и f → 0 {\ displaystyle {\ vec {f}} \! _ {0}} - произвольный вектор. Если f → 1, f → 2 {\ displaystyle {\ vec {f}} \! _ {1}, {\ vec {f}} \! _ {2}}
- произвольный вектор. Если f → 1, f → 2 {\ displaystyle {\ vec {f}} \! _ {1}, {\ vec {f}} \! _ {2}} являются устойчивыми столбцами матрицы A {\ displaystyle A}
являются устойчивыми столбцами матрицы A {\ displaystyle A} , единичный круг (cos (t), sin (t)) {\ displaystyle (\ cos (t), \ sin (t))}
, единичный круг (cos (t), sin (t)) {\ displaystyle (\ cos (t), \ sin (t))} , 0 ≤ t ≤ 2 π {\ displaystyle 0 \ leq t \ leq 2 \ pi}
, 0 ≤ t ≤ 2 π {\ displaystyle 0 \ leq t \ leq 2 \ pi} , отображается на эллипс:
, отображается на эллипс:
- x → = p → (t) = f → 0 + f → 1 cos t + f → 2 sin t. {\ displaystyle {\ vec {x}} = {\ vec {p}} (t) = {\ vec {f}} \! _ {0} + {\ vec {f}} \! _ {1} \ cos t + {\ vec {f}} \! _ {2} \ sin t \.}

Здесь f → 0 {\ displaystyle {\ vec {f}} \! _ {0}} - центр, а f → 1, f → 2 {\ displaystyle {\ vec {f}} \! _ {1}, \; {\ vec {f}} \! _ {2}}
- центр, а f → 1, f → 2 {\ displaystyle {\ vec {f}} \! _ {1}, \; {\ vec {f}} \! _ {2}} - это направления двух сопряженных диаметров, обычно не перпендикулярные.
- это направления двух сопряженных диаметров, обычно не перпендикулярные.
- вершины
Четыре вершины эллипса: p → (t 0), p → (t 0 ± π 2), p → (t 0 + π) {\ displaystyle {\ vec {p}} ( t_ {0}), \; {\ vec {p}} \ left (t_ {0} \ pm {\ tfrac {\ pi} {2}} \ right), \; {\ vec {p}} \ left (t_ {0} + \ pi \ right)} , для проекта t = t 0 {\ displaystyle t = t_ {0}}
, для проекта t = t 0 {\ displaystyle t = t_ {0}} определенного количества:
определенного количества:
- детская кроватка (2 t 0) = f → 1 2 - f → 2 2 2 f → 1 ⋅ f → 2. {\ displaystyle \ cot (2t_ {0}) = {\ гидроразрыв {{\ vec {f}} \! _ {1} ^ {\, 2} - {\ vec {f}} \! _ {2} ^ {\, 2}} {2 {\ vec {f}} \! _ {1} \ cdot {\ vec {f}} \! _ {2}}}.}

(Если f → 1 ⋅ f → 2 = 0 {\ displaystyle {\ vec {f}} \! _ {1} \ cdot {\ vec {f}} \! _ {2} = 0} , затем t 0 = 0 {\ displaystyle t_ {0} = 0}
, затем t 0 = 0 {\ displaystyle t_ {0} = 0} .) Это выводится следующим образом. Касательный вектор в точке p → (t) {\ displaystyle {\ vec {p}} (t)}
.) Это выводится следующим образом. Касательный вектор в точке p → (t) {\ displaystyle {\ vec {p}} (t)} равенство:
равенство:
- p → ′ (t) = - f → 1 sin t + f → 2 cos t. {\ displaystyle {\ vec {p}} \, '(t) = - {\ vec {f}} \! _ {1} \ sin t + {\ vec {f}} \! _ {2} \ cos t \.}

При параметре вершины t = t 0 {\ displaystyle t = t_ {0}} касательная перпендикулярна большая / вспомогательной осям, поэтому:
касательная перпендикулярна большая / вспомогательной осям, поэтому:
- 0 = p → ′ (t) ⋅ (p → (t) - f → 0) = (- f → 1 sin t + f → 2 cos t) ⋅ (f → 1 cos t + f → 2 sin т). {\ displaystyle 0 = {\ vec {p}} '(t) \ cdot \ left ({\ vec {p}} (t) - {\ vec {f}} \! _ {0} \ right) = \ left (- {\ vec {f}} \! _ {1} \ sin t + {\ vec {f}} \! _ {2} \ cos t \ right) \ cdot \ left ({\ vec {f} } \! _ {1} \ cos t + {\ vec {f}} \! _ {2} \ sin t \ right).}

Расширение и применение тождеств cos 2 t - sin 2 t знак равно соз 2 T, 2 грех T соз T знак равно грех 2 t {\ displaystyle \ cos ^ {2} t- \ sin ^ {2} t = \ cos 2t, \ \ 2 \ sin t \ cos t = \ sin 2t} дает уравнение для t = t 0 {\ displaystyle t = t_ {0}}
дает уравнение для t = t 0 {\ displaystyle t = t_ {0}} .
.
- неявного представления
Решение параметрического представления для cos т, грех т {\ displaystyle \; \ cos t, \ sin t \;} по правилу Крамера и с использованием cos 2 t + sin 2 t - 1 = 0 {\ displaystyle \; \ cos ^ {2} t + \ sin ^ {2} t-1 = 0 \;}
по правилу Крамера и с использованием cos 2 t + sin 2 t - 1 = 0 {\ displaystyle \; \ cos ^ {2} t + \ sin ^ {2} t-1 = 0 \;} , получается неявное представление
, получается неявное представление
- det (x → - f → 0, f → 2) 2 + det (е → 1, x → - f → 0) 2 - det (f → 1, f → 2) 2 = 0 {\ displaystyle \ det ({\ vec {x}} \! - \! {\ vec { f}} \! _ {0}, {\ vec {f}} \! _ {2}) ^ {2} + \ det ({\ vec {f}} \! _ {1}, {\ vec { x}} \! - \! {\ Vec {f}} \! _ {0}) ^ {2} - \ det ({\ vec {f}} \! _ {1}, {\ vec {f} } \! _ {2}) ^ {2} = 0}
 .
.
- Определение эллипса в этом разделе дает параметрическое представление произвольноголипса, даже в пространстве, если можно f → 0, f → 1, е → 2 {\ displaystyle {\ vec {f}} \! _ {0}, {\ vec {f}} \! _ {1}, {\ vec {f}} \! _ {2}}
 быть векторми в дизайне.
быть векторми в дизайне.Полярные формы
Полярные формы относительно центра
 Полярные координаты с центром в центре.
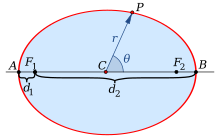
Полярные координаты с центром в центре. В полярных координатах, с началом в центре эллипса и с угловой координатой θ {\ displaystyle \ theta} , измеренной от большой оси, уравнение эллипса имеет вид
, измеренной от большой оси, уравнение эллипса имеет вид
- р (θ) знак равно ab (b соз θ) 2 + (грех θ) 2 знак равно б 1 - (е соз θ) 2 {\ displaystyle r (\ theta) = {\ frac {ab} {\ sqrt {(b \ cos \ theta) ^ {2} + (a \ sin \ theta) ^ {2}}}} = {\ frac {b} {\ sqrt {1- (e \ cos \ theta) ^ { 2}}}}

Полярная форма относительно фокуса
 Полярные координаты с центром в фокусе.
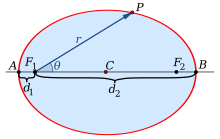
Полярные координаты с центром в фокусе. Если вместо этого мы будем использовать полярные координаты с началом в одном фокусе, с угловой координатой θ = 0 {\ displaystyle \ theta = 0} , все еще измеренной от большой оси уравнения эллипса имеет вид
, все еще измеренной от большой оси уравнения эллипса имеет вид
- r (θ) = a (1 - e 2) 1 ± e cos θ {\ displaystyle r (\ theta) = {\ frac {a (1-e ^ {2})} {1 \ pm e \ cos \ theta}}}

где знак в знаменателе отрицательный, если направление ссылки θ = 0 {\ displaystyle \ theta = 0} указывает к центру (как показано справа), и положительно, если это направление указывает от центра.
указывает к центру (как показано справа), и положительно, если это направление указывает от центра.
В немного более общем случае эллипса с одним фокусом в начале и другим фокусом в угловой координате ϕ {\ displaystyle \ phi} , полярная форма имеет вид
, полярная форма имеет вид
- r = a (1 - e 2) 1 - e cos (θ - ϕ). {\ displaystyle r = {\ frac {a (1-e ^ {2})} {1-e \ cos (\ theta - \ phi)}}.}

Угол θ {\ displaystyle \ theta } в этих формулах называется истинной аномалией точки. Числителем этой формул является прямая полушария прямой кишки ℓ = a (1 - e 2) {\ displaystyle \ ell = a (1-e ^ {2})}
в этих формулах называется истинной аномалией точки. Числителем этой формул является прямая полушария прямой кишки ℓ = a (1 - e 2) {\ displaystyle \ ell = a (1-e ^ {2})} .
.
Эксцентриситет и свойство directrix
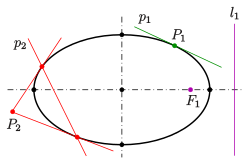
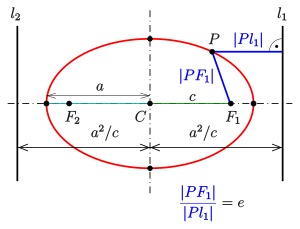 Эллипс: свойство directrix
Эллипс: свойство directrix Каждая из двух линий, параллельных малой оси, и на расстоянии d = a 2 c = ae {\ displaystyle d = {\ frac {a ^ {2}} {c} } = {\ frac {a} {e}}} от него, называется директрисой эллипса (см. Диаграмму).
от него, называется директрисой эллипса (см. Диаграмму).
- Для произвольной точки P {\ displaystyle P}
 эллипса отношение расстояния до одного фокуса и соответствующей направляющей (см. Диаграмму) равно эксцентриситету:
эллипса отношение расстояния до одного фокуса и соответствующей направляющей (см. Диаграмму) равно эксцентриситету: - | P F 1 | | P l 1 | = | P F 2 | | P l 2 | = е = с а. {\ displaystyle {\ frac {\ left | PF_ {1} \ right |} {\ left | Pl_ {1} \ right |}} = {\ frac {\ left | PF_ {2} \ right |} {\ left | Pl_ {2} \ right |}} = e = {\ frac {c} {a}} \.}

Доказательство для пары F 1, l 1 {\ displaystyle F_ {1}, l_ {1}} следует из того, что | P F 1 | 2 = (x - c) 2 + y 2, | P l 1 | 2 знак равно (Икс - a 2 с) 2 {\ Displaystyle \ left | PF_ {1} \ right | ^ {2} = (xc) ^ {2} + y ^ {2}, \ \ left | Pl_ {1} \ right | ^ {2} = \ left (x - {\ tfrac {a ^ {2}} {c}} \ right) ^ {2}}
следует из того, что | P F 1 | 2 = (x - c) 2 + y 2, | P l 1 | 2 знак равно (Икс - a 2 с) 2 {\ Displaystyle \ left | PF_ {1} \ right | ^ {2} = (xc) ^ {2} + y ^ {2}, \ \ left | Pl_ {1} \ right | ^ {2} = \ left (x - {\ tfrac {a ^ {2}} {c}} \ right) ^ {2}} и y 2 = b 2 - b 2 a 2 x 2 {\ displaystyle y ^ {2} = b ^ {2} - {\ tfrac {b ^ {2}} {a ^ {2}}} x ^ {2}}
и y 2 = b 2 - b 2 a 2 x 2 {\ displaystyle y ^ {2} = b ^ {2} - {\ tfrac {b ^ {2}} {a ^ {2}}} x ^ {2}} удовлетворяют уравнению
удовлетворяют уравнению
- | P F 1 | 2 - с 2 а 2 | P l 1 | 2 = 0. {\ displaystyle \ left | PF_ {1} \ right | ^ {2} - {\ frac {c ^ {2}} {a ^ {2}}} \ left | Pl_ {1} \ right | ^ {2} = 0 \.}

Второй случай доказывается аналогично.
Обратное также верно и может использоваться для определения эллипса (аналогично определению параболы):
- Для любой точки F {\ displaystyle F}
 (фокус), любая строка l {\ displaystyle l}
(фокус), любая строка l {\ displaystyle l} (directrix) не через F {\ displaystyle F}
(directrix) не через F {\ displaystyle F} и любое действительное число e {\ displaystyle e}
и любое действительное число e {\ displaystyle e} с 0 < e < 1, {\displaystyle 0
с 0 < e < 1, {\displaystyle 0 эллипс - это геометрическое место точек, для которых отношение расстояний до точки и линии равно e, {\ displaystyle e, }
эллипс - это геометрическое место точек, для которых отношение расстояний до точки и линии равно e, {\ displaystyle e, } то есть:
то есть: - E = {P | | P F | | P l | = e}. {\ Displaystyle E = \ left \ {P \ \ left | \ {\ frac {| PF |} {| Pl |}} = e \ right. \ right \}.}

Выбор e = 0 {\ displaystyle e = 0} , который является эксцентриситетом круга, не допускается в этом контексте. Можно считать, что директрисой окружности является бесконечно удаленная линия.
, который является эксцентриситетом круга, не допускается в этом контексте. Можно считать, что директрисой окружности является бесконечно удаленная линия.
(выбор e = 1 {\ displaystyle e = 1} дает параболу, и если e>1 {\ displaystyle e>1}
дает параболу, и если e>1 {\ displaystyle e>1} , гипербола.)
, гипербола.)
 Карандаш из коник с общей вершиной и общей полу-латусной прямой кишкой
Карандаш из коник с общей вершиной и общей полу-латусной прямой кишкой - Доказательство
Пусть F = (f, 0), e>0 {\ displaystyle F = (f, \, 0), \ e>0} и предположим, что (0, 0) {\ displaystyle (0, \, 0)}
и предположим, что (0, 0) {\ displaystyle (0, \, 0)} - точка на кривая. Директриса l {\ displaystyle l}
- точка на кривая. Директриса l {\ displaystyle l} имеет уравнение x = - f e {\ displaystyle x = - {\ tfrac {f} {e}}}
имеет уравнение x = - f e {\ displaystyle x = - {\ tfrac {f} {e}}} . При P = (x, y) {\ displaystyle P = (x, \, y)}
. При P = (x, y) {\ displaystyle P = (x, \, y)} отношение | P F | 2 = e 2 | P l | 2 {\ displaystyl e | PF | ^ {2} = e ^ {2} | Pl | ^ {2}}
отношение | P F | 2 = e 2 | P l | 2 {\ displaystyl e | PF | ^ {2} = e ^ {2} | Pl | ^ {2}} дает уравнения
дает уравнения
- (x - f) 2 + y 2 = e 2 (x + fe) 2 = (ex + f) 2 {\ displaystyle (xf) ^ {2 } + y ^ {2} = e ^ {2} \ left (x + {\ frac {f} {e}} \ right) ^ {2} = (ex + f) ^ {2}}
 и x 2 (e 2-1) + 2 xf (1 + e) - y 2 = 0. {\ displaystyle x ^ {2} \ left (e ^ {2} -1 \ right) + 2xf (1 + e) -y ^ {2} = 0.}
и x 2 (e 2-1) + 2 xf (1 + e) - y 2 = 0. {\ displaystyle x ^ {2} \ left (e ^ {2} -1 \ right) + 2xf (1 + e) -y ^ {2} = 0.}
Подстановка p = f (1 + e) {\ displaystyle p = f (1 + e)} возвращает
возвращает
- x 2 (e 2-1) + 2 px - y 2 = 0. {\ displaystyle x ^ {2} \ left (e ^ {2} -1 \ right) + 2px- y ^ {2} = 0.}

Это уравнение эллипса (e < 1 {\displaystyle e<1} ) или параболы (e = 1 {\ displaystyle e = 1}
) или параболы (e = 1 {\ displaystyle e = 1} ) или гипербола (e>1 {\ displaystyle e>1}
) или гипербола (e>1 {\ displaystyle e>1} ). Все эти невырожденные коники имеют общее начало в виде вершины (см. диаграмму).
). Все эти невырожденные коники имеют общее начало в виде вершины (см. диаграмму).
Если e < 1 {\displaystyle e<1} , введите новые параметры a, b {\ displaystyle a, \, b}
, введите новые параметры a, b {\ displaystyle a, \, b} так что 1 - e 2 = b 2 a 2 и p = b 2 a {\ displaystyle 1-e ^ {2} = {\ tfrac {b ^ { 2}} {a ^ {2}}}, {\ text {and}} \ p = {\ tfrac {b ^ {2}} {a}}}
так что 1 - e 2 = b 2 a 2 и p = b 2 a {\ displaystyle 1-e ^ {2} = {\ tfrac {b ^ { 2}} {a ^ {2}}}, {\ text {and}} \ p = {\ tfrac {b ^ {2}} {a}}} , а приведенное выше уравнение принимает вид
, а приведенное выше уравнение принимает вид
- (x - a) 2 a 2 + y 2 b 2 = 1, {\ displaystyle {\ frac {(xa) ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}} = 1 \,}

который представляет собой уравнение эллипса с центром (a, 0) {\ displaystyle (a, \, 0)} , ось x как большая ось и большая / малая полуось a, b {\ displaystyle a, \, b}
, ось x как большая ось и большая / малая полуось a, b {\ displaystyle a, \, b} .
.
- Общий эллипс
Если фокус F = (f 1, f 2) {\ Displaystyle F = \ left (f_ {1}, \, f_ {2} \ right)} и директриса ux + vy + w = 0 {\ displaystyle ux + vy + w = 0}
и директриса ux + vy + w = 0 {\ displaystyle ux + vy + w = 0} , уравнение
, уравнение
- (x - f 1) 2 + (y - f 2) 2 = e 2 (ux + vy + w) 2 u 2 + v 2. {\ displaystyle \ left (x-f_ {1} \ right) ^ {2} + \ left (y-f_ {2} \ right) ^ {2} = e ^ {2} {\ frac {\ left (ux + vy + w \ right) ^ {2}} {u ^ {2} + v ^ {2}}} \.}

(В правой части уравнения используется нормальная форма Гессе линии для вычислений расстояния | P l | {\ displaystyle | Pl |} .)
.)
Свойство отражения в фокусе
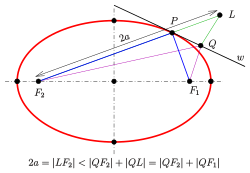 Эллипс: касательная делит пополам дополнительный угол между линиями и фокусами.
Эллипс: касательная делит пополам дополнительный угол между линиями и фокусами. 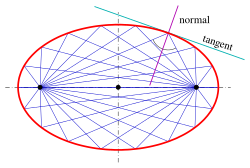 Лучи из одного фокуса отражаются от эллипса и проходят через другой фокус.
Лучи из одного фокуса отражаются от эллипса и проходят через другой фокус. Эллипс следующим образом:
- Нормаль в точке P {\ displaystyle P}
 делит пополам угол между линиями PF 1 ¯, PF 2 ¯ {\ displaystyle {\ overline { PF_ {1}}}, \, {\ overline {PF_ {2}}}}
делит пополам угол между линиями PF 1 ¯, PF 2 ¯ {\ displaystyle {\ overline { PF_ {1}}}, \, {\ overline {PF_ {2}}}} .
.
- Доказательство
Потому что касательная перпендикулярная нормали, утверждение верно и для касательной и дополнительного угла угла между линиями к фокусам (см. Диаграмму).
Пусть L {\ displaystyle L} будет точкой на линии PF 2 ¯ {\ displaystyle {\ overline {PF_ {2}}}}
будет точкой на линии PF 2 ¯ {\ displaystyle {\ overline {PF_ {2}}}} с расстояниями 2 a {\ displaystyle 2a}
с расстояниями 2 a {\ displaystyle 2a} до фокуса F 2 {\ displaystyle F_ {2}}
до фокуса F 2 {\ displaystyle F_ {2}} , a {\ displaystyle a}
, a {\ displaystyle a} - большая полуось эллипса. Пусть линия w {\ displaystyle w}
- большая полуось эллипса. Пусть линия w {\ displaystyle w} будет биссектрисой дополнительного угла к углу между линиями PF 1 ¯, PF 2 ¯ {\ displaystyle {\ overline {PF_ {1}}}, \, {\ overline {PF_ {2}}}}
будет биссектрисой дополнительного угла к углу между линиями PF 1 ¯, PF 2 ¯ {\ displaystyle {\ overline {PF_ {1}}}, \, {\ overline {PF_ {2}}}} . Чтобы доказать, что w {\ displaystyle w}
. Чтобы доказать, что w {\ displaystyle w} является касательной в точке P {\ displaystyle P}
является касательной в точке P {\ displaystyle P} , проверяется, что любая точка Q {\ displaystyle Q}
, проверяется, что любая точка Q {\ displaystyle Q} в строке w {\ displaystyle w}
в строке w {\ displaystyle w} , что отличается от P {\ displaystyle P}
, что отличается от P {\ displaystyle P} , не может быть на эллипсе. Следовательно, w {\ displaystyle w}
, не может быть на эллипсе. Следовательно, w {\ displaystyle w} имеет только точку P {\ displaystyle P}
имеет только точку P {\ displaystyle P} , общую с эллипсом, и, следовательно, является касательной в точке P {\ displaystyle P}
, общую с эллипсом, и, следовательно, является касательной в точке P {\ displaystyle P} .
.
Из диаграммы и неравенства треугольника видно, что 2 a = | L F 2 | < | Q F 2 | + | Q L | = | Q F 2 | + | Q F 1 | {\displaystyle 2a=\left|LF_{2}\right|<\left|QF_{2}\right|+\left|QL\right|=\left|QF_{2}\right|+\left|QF_{1}\right|} удерживается, что означает: | Q F 2 | + | Q F 1 |>2 а {\ displaystyle \ left | QF_ {2} \ right | + \ влево | QF_ {1} \ right |>2a}
удерживается, что означает: | Q F 2 | + | Q F 1 |>2 а {\ displaystyle \ left | QF_ {2} \ right | + \ влево | QF_ {1} \ right |>2a} . Но если Q {\ displaystyle Q}
. Но если Q {\ displaystyle Q} - это точка эллипса, сумма должна быть 2 a {\ displaystyle 2a}
- это точка эллипса, сумма должна быть 2 a {\ displaystyle 2a} .
.
- Приложение
Лучи из одного фокуса отражаются эллипсом во втором положении. Это свойство имеет оптические и акустические приложения, аналогичные отражательные свойства параболы (см. шепчущая галерея ).
Сопряженные диаметры
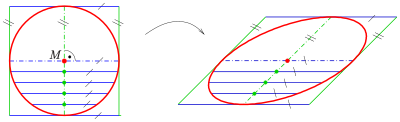 Ортогональныерыры. Окружность с квадратом касательных, серединами параллельных хорд и аффинным изображением, которое эллипс с сопряженными диаметрами, параллелограмм касательных и середины хорд.
Ортогональныерыры. Окружность с квадратом касательных, серединами параллельных хорд и аффинным изображением, которое эллипс с сопряженными диаметрами, параллелограмм касательных и середины хорд. Окружность имеет следующее свойство:
- Передние параллельные хорд лежат на диаметре.
Аффинное преобразование параллелизм и середины. прямой сегмент, поэтому это свойство верно для любого эллипса. орды и диаметр больше не ортогональны.)
- Определение
Два диаметра d 1, d 2 {\ displaystyle d_ {1}, \, d_ {2}} эллипса сопряжены, если середины хорд, параллельные d 1 {\ displaystyle d_ {1}}
эллипса сопряжены, если середины хорд, параллельные d 1 {\ displaystyle d_ {1}} , лежат на d 2. {\ displaystyle d_ {2} \.}
, лежат на d 2. {\ displaystyle d_ {2} \.}
Из диаграммы можно найти:
- Два диаметра P 1 Q 1 ¯, P 2 Q 2 ¯ {\ displaystyle {\ overline {P_ {1} Q_ {1}}}, \, {\ overline {P_ {2} Q_ {2}}}}
 эллипса сопряжены, если касательные в точке P 1 {\ displaystyle P_ {1}}
эллипса сопряжены, если касательные в точке P 1 {\ displaystyle P_ {1}} и Q 1 {\ displaystyle Q_ { 1}}
и Q 1 {\ displaystyle Q_ { 1}} параллельны P 2 Q 2 ¯ {\ displaystyle {\ overline {P_ {2} Q_ {2}}}}
параллельны P 2 Q 2 ¯ {\ displaystyle {\ overline {P_ {2} Q_ {2}}}} .
.
Сопряженные диаметры в эллипсе обобщают ортогональные диаметры в окружности.
В параметрическом уравнении для общего эллипса, приведенном выше,
- x → = p → (t) = f → 0 + f → 1 cos t + f → 2 sin t, {\ displaystyle { \ vec {x}} = {\ vec {p}} (t) = {\ vec {f}} \! _ {0} + {\ vec {f}} \! _ {1} \ cos t + {\ vec {f}} \! _ {2} \ sin t,}

любая пара точек p → (t), p → (t + π) {\ displaystyle {\ vec {p}} (t), \ {\ vec { p}} (t + \ pi)} принадлежат диаметру, а пара p → (t + π 2), p → (t - π 2) {\ displaystyle {\ vec {p} } \ left (t + {\ tfrac {\ pi} {2}} \ right), \ {\ vec {p}} \ left (t - {\ tfrac {\ pi} {2}} \ right)}
принадлежат диаметру, а пара p → (t + π 2), p → (t - π 2) {\ displaystyle {\ vec {p} } \ left (t + {\ tfrac {\ pi} {2}} \ right), \ {\ vec {p}} \ left (t - {\ tfrac {\ pi} {2}} \ right)} принадлежат его сопряженному диаметру.
принадлежат его сопряженному диаметру.
Теорема Аполлония о сопряженных диаметрах
 Эллипс: теорема Аполлония о сопряженных диаметрах
Эллипс: теорема Аполлония о сопряженных диаметрах Для эллипса с полуосями a, b {\ displaystyle a, \, b} верно следующее:
верно следующее:
- Пусть c 1 {\ displaystyle c_ {1}}
 и c 2 {\ displaystyle c_ {2}}
и c 2 {\ displaystyle c_ {2}} быть половинками двух сопряженных диаметров (см. Диаграмму), тогда
быть половинками двух сопряженных диаметров (см. Диаграмму), тогда - c 1 2 + c 2 2 = a 2 + b 2 {\ displaystyle c_ {1} ^ {2} + c_ {2} ^ {2} = a ^ {2} + b ^ {2}}
 ,
, - треугольник, образованный c 1, c 2 {\ displaystyle c_ {1}, \, c_ {2}}
 , имеет постоянную площадь A Δ = 1 2 ab {\ textstyle A _ {\ Delta} = {\ frac {1} {2}} ab}
, имеет постоянную площадь A Δ = 1 2 ab {\ textstyle A _ {\ Delta} = {\ frac {1} {2}} ab}
- параллелограмм касательных, примыкающих к данным сопряженным диаметром, имеет Площадь 12 = 4 пр. {\ displaystyle {\ text {Area}} _ {12} = 4ab \.}

- Доказательство
Пусть эллипс имеет каноническую форму с параметрическим уравнением
- p → (t) = (a cos t, b грех t) {\ displaystyle {\ vec {p}} (t) = (a \ cos t, \, b \ sin t)}
 .
.
Две точки c → 1 = p → (т), с → 2 знака равно п → (т + π 2) {\ displaystyle {\ vec {c}} _ {1} = {\ vec {p}} (т), \ {\ vec {c}} _ {2 } = {\ vec {p}} \ left (t + {\ frac {\ pi} {2}} \ right)} имеют сопряженные диаметры (см. Предыдущий раздел). Из тригонометрических формул получаем c → 2 = (- грех t, b cos t) T {\ displaystyle {\ vec {c}} _ {2} = (- a \ sin t, \, b \ cos t) ^ {\ mathsf {T}}}
имеют сопряженные диаметры (см. Предыдущий раздел). Из тригонометрических формул получаем c → 2 = (- грех t, b cos t) T {\ displaystyle {\ vec {c}} _ {2} = (- a \ sin t, \, b \ cos t) ^ {\ mathsf {T}}} и
и
- | c → 1 | 2 + | c → 2 | 2 знак равно ⋯ знак равно а 2 + Ь 2. {\ displaystyle \ left | {\ vec {c}} _ {1} \ right | ^ {2} + \ left | {\ vec {c}} _ {2} \ right | ^ {2} = \ cdots = a ^ {2} + b ^ {2} \.}

Площадь треугольника, образованная c → 1, c → 2 {\ displaystyle {\ vec {c}} _ {1}, \, {\ vec {c}} _ {2}} равно
равно
- A Δ = 1 2 det (c → 1, c → 2) = ⋯ = 1 2 ab { \ displaystyle A _ {\ Дельта} = {\ frac {1} {2}} \ det \ left ({\ vec {c}} _ {1}, \, {\ vec {c}} _ {2} \ справа) = \ cdots = {\ frac {1} {2}} ab}

и из диаграммы видно, что площадь параллелограмма в 8 раз больше, чем у A Δ {\ displaystyle A _ {\ Delta} } . Следовательно,
. Следовательно,
- Площадь 12 = 4 a b. {\ displaystyle {\ text {Area}} _ {12} = 4ab \.}

Ортогональные касательные
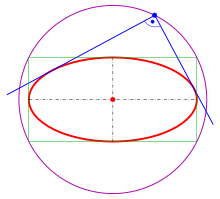 Эллипс с его ортоптиком
Эллипс с его ортоптиком Для эллипса x 2 a 2 + y 2 b 2 = 1 {\ displaystyle {\ tfrac {x ^ {2}} {a ^ {2}}} + {\ tfrac {y ^ {2}} {b ^ {2}}} = 1} точка пересечения ортогональных касательных лежат на окружности x 2 + y 2 = a 2 + b 2 {\ displaystyle x ^ {2} + y ^ {2} = a ^ {2} + b ^ {2}}
точка пересечения ортогональных касательных лежат на окружности x 2 + y 2 = a 2 + b 2 {\ displaystyle x ^ {2} + y ^ {2} = a ^ {2} + b ^ {2}} .
.
Эта окружность называется ортоптической или направляющей окружностью эллипса (не путать с круговой направляющей, тип выше).
Рисование эллипсов
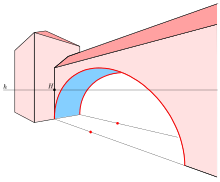 Центральная проекция окружностей (затвор)
Центральная проекция окружностей (затвор) Эллипсы появляются в описательной геометрии как изображения (параллельная или центральная проекция) окружностей. Существуют различные инструменты для рисования эллипса. Компьютеры обеспечивают самый быстрый и точный метод рисования эллипса. Однако технические средства (эллипсографы ) для рисования эллипса без использования компьютера существуют. Принцип эллипсографов был известен греческим математикам, таким как Архимед и Проклос.
. Если эллипсограф недоступен, можно нарисовать эллипс, используя аппроксимацию четырьмя соприкасающимися кругами на вершины.
Для любого метода, ниже, необходимо знание осей и полуосей (или, что эквивалентно: фокусов и большой полуоси). Если это предположение не выполнено, необходимо знать как минимум два сопряженных диаметра. С помощью конструкции Ритца оси и полуоси могут быть восстановлены.
Построение точки де Ла Хира
Следующее построение отдельных точек эллипса связано с де Ла Хиром. Он основан на стандартном параметрическом представлении (a cos t, b sin t) {\ displaystyle (a \ cos t, \, b \ sin t)} эллипса :
эллипса :
- Нарисуйте две окружности в центре эллипса с радиусами a, b {\ displaystyle a, b}
 и осями эллипса.
и осями эллипса. - Проведите линию через центр, которая пересекает два круга в точке A {\ displaystyle A}
 и B {\ displaystyle B}
и B {\ displaystyle B} соответственно..
соответственно.. - Проведите линию через A {\ displaystyle A}
 , которая параллельна малой оси, и линию через B {\ displaystyle B}
, которая параллельна малой оси, и линию через B {\ displaystyle B} , которая параллельна большой оси. Эти линии пересекаются в точке эллипса (см. Диаграмму).
, которая параллельна большой оси. Эти линии пересекаются в точке эллипса (см. Диаграмму). - Повторите шаги (2) и (3) с разными линиями через центр.

Метод де Ла Хира
Анимация метода
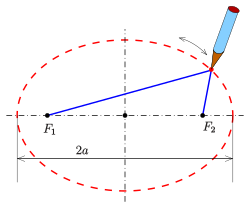 Эллипс: метод садовника
Эллипс: метод садовника Метод булавок и цепочек
Характеристика эллипса как геометрического места точек, так что сумма расстояний до фокусов постоянна, приводит к методу рисования одного из двух булавки для рисования, веревка и карандаш. В этом методе булавки вставляются в бумагу в двух точках, которые становятся фокусами эллипса. На каждом конце к двум булавкам привязывается веревка; его длина после связывания составляет 2 a {\ displaystyle 2a} . Затем кончик карандаша образует эллипс, если его перемещать, сохраняя натянутую нить. Используя два колышка и веревку, садовники используют эту власть, чтобы очертить эллиптические клумбу, она называется эллипсом садовника поэтому.
. Затем кончик карандаша образует эллипс, если его перемещать, сохраняя натянутую нить. Используя два колышка и веревку, садовники используют эту власть, чтобы очертить эллиптические клумбу, она называется эллипсом садовника поэтому.
Подобный метод рисования конфокальных эллипсов с замкнутой цепочкой был разработан ирландским епископом Чарльзом Грейвсом.
Методы бумажной ленты
Два следующих метода использования на параметрическом представлении (см.. параметрическое представление выше):
- (a cos t, b sin t) {\ displaystyle (a \ cos t, \, b \ sin t)}

Технически это представление можно смоделировать двумя простыми способами. В обоих случаях центр оси и полуоси a, b {\ displaystyle a, \, b} должны быть известны.
должны быть известны.
- Метод 1
Первый метод начинается с
- полосы бумаги длиной a + b {\ displaystyle a + b}
 .
.
Точка, где встречаются полуоси, отмечена P {\ displaystyle P} . Если полоса скользит обоими концами по осям желаемого эллипса, то точка P отслеживает эллипс. Для доказательства показана точка P {\ displaystyle P}
. Если полоса скользит обоими концами по осям желаемого эллипса, то точка P отслеживает эллипс. Для доказательства показана точка P {\ displaystyle P} имеет параметрическое представление (a cos t, b sin t) {\ displaystyle (a \ cos t, \, b \ sin t)}
имеет параметрическое представление (a cos t, b sin t) {\ displaystyle (a \ cos t, \, b \ sin t)} , где параметр t {\ displaystyle t}
, где параметр t {\ displaystyle t} - угол наклона бумажной полосы.
- угол наклона бумажной полосы.
Техническая реализация бумажной ленты может быть достигнута с помощью пары Туси (см. Анимацию). Устройство способно нарисовать любой эллипс с фиксированной суммой a + b {\ displaystyle a + b} , которая является охраной большого круга. Это ограничение может быть недостатком в реальной жизни. Более гибким является второй метод бумажной ленты.
, которая является охраной большого круга. Это ограничение может быть недостатком в реальной жизни. Более гибким является второй метод бумажной ленты.
Вариант метода 1 с бумажной полоской использует наблюдение, что средняя точка N \ displaystyle N} бумажной полоски перемещается по окружности с центром M {\ displaystyle M}
бумажной полоски перемещается по окружности с центром M {\ displaystyle M} (эллипса) и радиус a + b 2 {\ displaystyle {\ tfrac {a + b} {2}}}
(эллипса) и радиус a + b 2 {\ displaystyle {\ tfrac {a + b} {2}}} . Следовательно, полоску бумаги можно разрезать в точке N {\ displaystyle N}
. Следовательно, полоску бумаги можно разрезать в точке N {\ displaystyle N} на половинки, снова соединенные стыком в точке N {\ displaystyle N}
на половинки, снова соединенные стыком в точке N {\ displaystyle N} и скользящий конец K {\ displaystyle K}
и скользящий конец K {\ displaystyle K} закреплен в центре M {\ displaystyle M}
закреплен в центре M {\ displaystyle M} (см. Диаграмму). После этой операции изменить половину полоски бумаги не изменяется. Этот вариант требует только одного скользящего башмака.
(см. Диаграмму). После этой операции изменить половину полоски бумаги не изменяется. Этот вариант требует только одного скользящего башмака.
 Построение эллипса: метод 2 полосы бумаги
Построение эллипса: метод 2 полосы бумаги - Метод 2
Второй метод начинается с
- a полоска бумаги длиной a {\ displaystyle a}
 .
.
Одна отмечает точку, которая делит полосу на две части длиной b {\ displaystyle b} и а - b {\ displaystyle ab}
и а - b {\ displaystyle ab} . Полоса размещается на осях, как показано на схеме. Затем свободный конец полоски очерчивает эллипс, при этом полоска перемещается. Для доказательства следует установить, что точка может быть описана параметрами как (a cos t, b sin t) {\ displaystyle (a \ cos t, \, b \ sin t)}
. Полоса размещается на осях, как показано на схеме. Затем свободный конец полоски очерчивает эллипс, при этом полоска перемещается. Для доказательства следует установить, что точка может быть описана параметрами как (a cos t, b sin t) {\ displaystyle (a \ cos t, \, b \ sin t)} , где параметр t {\ displaystyle t}
, где параметр t {\ displaystyle t} - угол наклона бумажной полосы.
- угол наклона бумажной полосы.
Этот метод используется для нескольких эллипсографов (см. Раздел ниже).
Аналогичным способом способом 1 с бумажной полосой, можно найти вариант способа 2 с бумажной полосой (см. Диаграмму) путем разрезания части между осями пополам.
Большинство эллипсографов чертежей основы на второй метод бумажной ленты.
 Аппроксимация эллипса, соприкасающиеся кругами
Аппроксимация эллипса, соприкасающиеся кругами Аппроксимация соприкасаса разными кругами
Из метрических свойств, приведенных ниже, можно получить:
- Радиус кривизны в вершинах V 1, V 2 {\ displaystyle V_ {1 }, \, V_ {2}}
 это: b 2 a {\ displaystyle {\ tfrac {b ^ {2}} {a}}}
это: b 2 a {\ displaystyle {\ tfrac {b ^ {2}} {a}}}
- Радиус кривизны на совпадающих вершинах V 3, V 4 {\ displaystyle V_ {3}, \, V_ {4}}
 равенство: a 2 b. {\ displaystyle {\ tfrac {a ^ {2}} {b}} \.}
равенство: a 2 b. {\ displaystyle {\ tfrac {a ^ {2}} {b}} \.}
На схеме показан простой способ найти центры кривизны C 1 = (a - b 2 a, 0), С 3 знак равно (0, b - a 2 b) {\ displaystyle C_ {1} = \ left (a - {\ tfrac {b ^ {2}} {a}}, 0 \ right), \, C_ {3} = \ left (0, b - {\ tfrac {a ^ {2}} {b}} \ right)} в вершине V 1 {\ displaystyle V_ {1}}
в вершине V 1 {\ displaystyle V_ {1}} и совпадающая вершина V 3 {\ displaystyle V_ {3}}
и совпадающая вершина V 3 {\ displaystyle V_ {3}} соответственно:
соответственно:
- отмечает точку H = (a, b) {\ displaystyle H = (a, \, b)}
 и нарисуйте отрезок линии V 1 V 3, {\ displaystyle V_ {1} V_ {3} \,}
и нарисуйте отрезок линии V 1 V 3, {\ displaystyle V_ {1} V_ {3} \,}
- нарисуйте линию через H {\ displaystyle H}
 , которая перпендикулярна линии V 1 V 3, {\ displaystyle V_ {1} V_ {3} \,}
, которая перпендикулярна линии V 1 V 3, {\ displaystyle V_ {1} V_ {3} \,}
- пересечение точки этой линии с осями центрами соприкасающихся окружностей.
(доказательство: простой расчет).
Центры остальных вершин находятся симметрично.
С помощью французской строительной кривой С помощью французской строительной кривой, которая имеет плавный контакт с соприкаса нашими кругами.
Поколение Штейнера
 Эллипс: Поколение Штейнера
Эллипс: Поколение Штейнера  Эллипс: Поколение Штайнера
Эллипс: Поколение Штайнера Следующий метод построения отдельных точек эллипса основан на генерации Штейнера конического сечения сечения :
- Даны два карандаша B (U), B (V) {\ displaystyle B (U), \, B (V)}
 линий в двух точках U, V {\ displaystyle U, \, V}
линий в двух точках U, V {\ displaystyle U, \, V} (все строки, содержащие U \ displaystyle U}
(все строки, содержащие U \ displaystyle U} и V {\ displaystyle V}
и V {\ displaystyle V} соответственно) и проекционное, но не перспективное отображение π {\ displaystyle \ pi}
соответственно) и проекционное, но не перспективное отображение π {\ displaystyle \ pi} из B (U) {\ displaystyle B (U)}
из B (U) {\ displaystyle B (U)} на B (V) {\ displaystyle B (V)}
на B (V) {\ displaystyle B (V)} , то точки пересечения соответствующих прямых образуют невырожденное проективное коническое сечение.
, то точки пересечения соответствующих прямых образуют невырожденное проективное коническое сечение.
Для генерации точек эллипс x 2 a 2 + y 2 b 2 = 1 {\ displaystyle {\ tfrac {x ^ {2}} {a ^ {2}}} + {\ tfrac {y ^ { 2}} {b ^ {2}}} = 1} карандаши используются в вершинах V 1, V 2 {\ displaystyle V_ {1}, \, V_ {2}}
карандаши используются в вершинах V 1, V 2 {\ displaystyle V_ {1}, \, V_ {2}} . Пусть P = (0, b) {\ displaystyle P = (0, \, b)}
. Пусть P = (0, b) {\ displaystyle P = (0, \, b)} верхняя совершина эллипса и A = (- a, 2 б), В знак равно (а, 2 б) {\ Displaystyle А = (- а, \, 2b), \, В = (а, \, 2b)}
верхняя совершина эллипса и A = (- a, 2 б), В знак равно (а, 2 б) {\ Displaystyle А = (- а, \, 2b), \, В = (а, \, 2b)} .
.
Р {\ Displaystyle P} - центр прямоугольника V 1, V 2, B, A {\ displaystyle V_ {1}, \, V_ {2}, \, B, \, A}
- центр прямоугольника V 1, V 2, B, A {\ displaystyle V_ {1}, \, V_ {2}, \, B, \, A} . Сторона AB ¯ {\ displaystyle {\ overline {AB}}}
. Сторона AB ¯ {\ displaystyle {\ overline {AB}}} прямоугольное деление на равных отрезках прямой, и это деление проецируется параллельно параллонали AV 2 {\ displaystyle AV_ {2}}
прямоугольное деление на равных отрезках прямой, и это деление проецируется параллельно параллонали AV 2 {\ displaystyle AV_ {2}} в качестве направления на отрезок линии V 1 B ¯ {\ displaystyle {\ overline {V_ {1} B}}}
в качестве направления на отрезок линии V 1 B ¯ {\ displaystyle {\ overline {V_ {1} B}}} и назначьте деление, как показано на схеме. Параллельная проекция вместе с обратной ориентацией представляет собой часть проективного отображения карандашами в V 1 {\ displaystyle V_ {1}}
и назначьте деление, как показано на схеме. Параллельная проекция вместе с обратной ориентацией представляет собой часть проективного отображения карандашами в V 1 {\ displaystyle V_ {1}} и V 2 {\ displaystyle V_ {2}}
и V 2 {\ displaystyle V_ {2}} необходимо. Точки пересечения любых двух связанных линий V 1 B i {\ displaystyle V_ {1} B_ {i}}
необходимо. Точки пересечения любых двух связанных линий V 1 B i {\ displaystyle V_ {1} B_ {i}} и V 2 A i {\ displaystyle V_ {2} A_ {i} }
и V 2 A i {\ displaystyle V_ {2} A_ {i} } - точка однозначно определенного эллипса. С помощью точек C 1,… {\ displaystyle C_ {1}, \, \ dotsc}
- точка однозначно определенного эллипса. С помощью точек C 1,… {\ displaystyle C_ {1}, \, \ dotsc} можно определить точки второй четверти эллипса. Аналогичным образом точки нижней половины эллипса.
можно определить точки второй четверти эллипса. Аналогичным образом точки нижней половины эллипса.
Генерация Штейнера также может быть определена для гипербол и парабол. Иногда его используют методом параллелограммы, потому что можно использовать другие точки, а не вершины, которые начинается с параллелограммы вместо прямоугольника.
Как гипотрохоиды
 Эллипс (красный) как частный случай гипотрохоиды с R = 2r
Эллипс (красный) как частный случай гипотрохоиды с R = 2r Эллипс является частным случаем гипотрохоиды , когда R = 2r, как показано на соседнем изображении. Частный случай движущегося круга с радиусом r {\ displaystyle r} внутри круга с радиусом R = 2 r {\ displaystyle R = 2r}
внутри круга с радиусом R = 2 r {\ displaystyle R = 2r} - это называется пара Туси.
- это называется пара Туси.
Вписанные углы и трехточечная форма
Круги
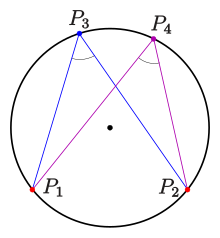 Круг: теорема о вписанном угле
Круг: теорема о вписанном угле Круг с уравнением (x - x ∘) 2 + (Y - Y ∘) 2 знак равно р 2 {\ displaystyle \ left (xx _ {\ circ} \ right) ^ {2} + \ left (yy _ {\ circ} \ right) ^ {2} = r ^ {2}} однозначно определяется тремя точками (x 1, y 1), (x 2, y 2), (x 3, y 3) {\ displaystyle \ left (x_ {1}, y_ {1} \ верно), \; \ left (x_ {2}, \, y_ {2} \ right), \; \ left (x_ {3}, \, y_ {3} \ right)}
однозначно определяется тремя точками (x 1, y 1), (x 2, y 2), (x 3, y 3) {\ displaystyle \ left (x_ {1}, y_ {1} \ верно), \; \ left (x_ {2}, \, y_ {2} \ right), \; \ left (x_ {3}, \, y_ {3} \ right)} не в строке. Простой способ определения параметров x ∘, y ∘, r {\ displaystyle x _ {\ circ}, y _ {\ circ}, r}
не в строке. Простой способ определения параметров x ∘, y ∘, r {\ displaystyle x _ {\ circ}, y _ {\ circ}, r} использует теорему о вписанном угле для кругов:
использует теорему о вписанном угле для кругов:
- Для четырех точек P i = (xi, yi), i = 1, 2, 3, 4, {\ displaystyle P_ {i} = \ left (x_ {i}, \, y_ {i} \ right), \ i = 1, \, 2, \, 3, \, 4, \,}
 (см. диаграмму) верно следующее утверждение:
(см. диаграмму) верно следующее утверждение: - Четыре точки находятся на окружности тогда и только тогда, когда углы равны P 3 {\ displaystyle P_ {3}}
 и P 4 {\ displaystyle P_ {4}}
и P 4 {\ displaystyle P_ {4}} равны.
равны.
Обычно вписанные углы измеряются градусом или радианом θ, но здесь более удобно следующее измерение:
- Чтобы измерить угол между двумя линиями с помощью уравнений y = m 1 Икс + d 1, Y знак равно м 2 Икс + d 2, м 1 ≠ м 2, {\ displaystyle y = m_ {1} x + d_ {1}, \ y = m_ {2} x + d_ {2}, \ m_ {1} \ neq m_ {2},}
 используется частное:
используется частное: - 1 + m 1 m 2 m 2 - m 1 = cot θ. {\ displaystyle {\ frac {1 + m_ {1} m_ {2}} {m_ {2} -m_ {1}}} = \ cot \ theta \.}

Теорема о вписанном угле для окружностей
Для четырех точек P i = (xi, yi), i = 1, 2, 3, 4, {\ displaystyle P_ {i} = \ left (x_ {i}, \, y_ {i}) \ справа), \ i = 1, \, 2, \, 3, \, 4, \,} нет трех из них на строке, мы имеем следующее (см. диаграмму):
нет трех из них на строке, мы имеем следующее (см. диаграмму):
- точки находятся на окружности, если и только если углы равны P 3 {\ displaystyle P_ {3}}
 и P 4 {\ displaystyle P_ {4}}
и P 4 {\ displaystyle P_ {4}} равны. В терминах измерения угла выше это означает:
равны. В терминах измерения угла выше это означает: - (x 4 - x 1) (x 4 - x 2) + (y 4 - y 1) (y 4 - y 2) (y 4 - y 1) (x 4 - x 2) - (y 4 - y 2) (x 4 - x 1) = (x 3 - x 1) (x 3 - x 2) + (y 3 - y 1) (y 3 - y 2) (y 3 - y 1) (x 3 - x 2) - (y 3 - y 2) (x 3 - x 1). {\ displaystyle {\ frac {(x_ {4} -x_ {1}) (x_ {4} -x_ {2}) + (y_ {4} -y_ {1}) (y_ {4} -y_ {2 })} {(y_ {4} -y_ {1}) (x_ {4} -x_ {2}) - (y_ {4} -y_ {2}) (x_ {4} -x_ {1})} } = {\ frac {(x_ {3} -x_ {1}) (x_ {3} -x_ {2}) + (y_ {3} -y_ {1}) (y_ {3} -y_ {2})} {(y_ {3} -y_ {1}) (x_ {3} -x_ {2}) - (y_ {3} -y_ {2}) (x_ {3} -x_ {1})}}.}

Сначала такт доступен только для хорд, не параллельных оси Y, но окончательная формула работает для любого аккорда.
Трехточечная форма уравнения круга
- Как следствие, получается уравнение для круга, определяемого тремя неколлинеарными точками P i = (xi, yi) {\ displaystyle P_ { i} = \ left (x_ {i}, \, y_ {i} \ right)}
 :
: - (x - x 1) (x - x 2) + (y - y 1) (y - y 2) ( y - y 1) (x - x 2) - (y - y 2) (x - x 1) = (x 3 - x 1) (x 3 - x 2) + (y 3 - y 1) (y 3 - y 2) (y 3 - y 1) (x 3 - x 2) - (y 3 - y 2) (x 3 - x 1). {\ displaystyle {\ frac {({\ color {red} x} -x_ {1}) ({\ color {red} x} -x_ {2}) + ({\ color {red} y} -y_ { 1}) ({\ цвет {красный} y} -y_ {2})} {({\ color {красный} y} -y_ {1}) ({\ color {красный} x} -x_ {2}) - ({\ color {red} y} -y_ {2}) ({\ color {red} x} -x_ {1})}} = {\ frac {(x_ {3} -x_ {1}) ( x_ {3} -x_ {2}) + (y_ {3} -y_ {1}) (y_ {3} -y_ {2})} {(y_ {3} -y_ {1}) (x_ {3 } -x_ {2}) - (y_ {3} -y_ {2}) (x_ {3} -x_ {1})}}.}

Например, для P 1 = (2, 0), п 2 знак равно (0, 1), п 3 знак равно (0, 0) {\ displaystyle P_ {1} = (2, \, 0), \; P_ {2} = (0, \, 1), \; P_ {3} = (0, \, 0)} трехточечное уравнение:
трехточечное уравнение:
- (x - 2) x + y (y - 1) yx - (y - 1) (х - 2) знак равно 0 {\ displaystyle {\ frac {(x-2) x + y (y-1)} {yx- (y-1) (x-2)}} = 0}
 , который можно переформатировать в (x - 1) 2 + (y - 1 2) 2 = 5 4. {\ displaystyle (x-1) ^ {2} + \ left (y - {\ tfrac {1} {2}} \ right) ^ {2} = {\ tfrac {5} {4}} \.}
, который можно переформатировать в (x - 1) 2 + (y - 1 2) 2 = 5 4. {\ displaystyle (x-1) ^ {2} + \ left (y - {\ tfrac {1} {2}} \ right) ^ {2} = {\ tfrac {5} {4}} \.}
Используя векторы, скалярные произведения и детерминанты, эту формулу можно упорядочить более четко, позволяя x → = (x, y) {\ displaystyle {\ vec {x} } = (x, \, y)} :
:
- (x → - x → 1) ⋅ (x → - x → 2) det (x → - x → 1, x → - x → 2) = (x → 3 - x → 1) ⋅ (x → 3 - x → 2) det (x → 3 - x → 1, x → 3 - x → 2). {\ displaystyle {\ frac {\ left ({\ color {red} {\ vec {x}}} - {\ vec {x}} _ {1} \ right) \ cdot \ left ({\ color {red}) {\ vec {x}}} - {\ vec {x}} _ {2} \ right)} {\ det \ left ({\ color {red} {\ vec {x}}} - {\ vec {x }} _ {1}, {\ color {red} {\ vec {x}}} - {\ vec {x}} _ {2} \ right)}} = {\ frac {\ left ({\ vec { x}} _ {3} - {\ vec {x}} _ {1} \ right) \ cdot \ left ({\ vec {x}} _ {3} - {\ vec {x}} _ {2} \ right)} {\ det \ left ({\ vec {x}} _ {3} - {\ vec {x}} _ {1}, {\ vec {x}} _ {3} - {\ vec { x}} _ {2} \ right)}}.}

Центр круга (x ∘, y ∘) {\ displaystyle \ left (x _ {\ circ}, \, y _ {\ circ } \ right)} удовлетворяет:
удовлетворяет:
- [1 y 1 - y 2 x 1 - x 2 x 1 - x 3 y 1 - y 3 1] [x ∘ y ∘] = [x 1 2 - x 2 2 + y 1 2 - y 2 2 2 (x 1 - x 2) y 1 2 - y 3 2 + x 1 2 - x 3 2 2 (y 1 - y 3)]. {\ displaystyle {\ begin {bmatrix} 1 {\ frac {y_ {1} -y_ {2}} {x_ {1} -x_ {2}}}\\ {\ frac {x_ {1} -x_ {3)}} {y_ {1} -y_ {3}}} 1 \ end {bmatrix}} {\ begin {bmatrix} x _ {\ circ} \ \ y _ {\ circ} \ end {bmatrix}} = {\ begin {bmatrix} {\ frac {x_ {1} ^ {2} -x_ {2} ^ {2} + y_ {1} ^ {2} -y_ {2} ^ {2}} {2 (x_ {1} - x_ {2})}} \\ {\ frac {y_ {1} ^ {2} -y_ {3} ^ {2} + x_ {1} ^ {2} -x_ {3} ^ {2}} {2 (y_ {1} -y_ {3})}} \ end {bmatrix}}.}

Радиус - это расстояние между любым из трех точек и центр.
- r = (x 1 - x ∘) 2 + (y 1 - y ∘) 2 = (x 2 - x ∘) 2 + (y 2 - y) 2 = (x 3 - x ∘) 2 + ( у 3 - у) 2. {\ displaystyle r = {\ sqrt {\ left (x_ {1} -x _ {\ circ} \ right) ^ {2} + \ left (y_ {1} -y _ {\ circ} \ right) ^ {2}}} = {\ sqrt {\ left (x_ {2} -x _ {\ circ} \ right) ^ {2} + \ left (y_ {2} -y _ {\ circ} \ right) ^ {2}}} = {\ sqrt {\ left (x_ {3} -x _ {\ circ} \ right) ^ {2} + \ left (y_ {3} -y _ {\ circ} \ right) ^ {2}}}.}

Эллипсы
В этом разделе мы рассматриваем семейство эллипсов, определяемым уравнением (x - x ∘) 2 a 2 + (y - y ∘) 2 б 2 знак равно 1 {\ displaystyle {\ tfrac {\ left (xx _ {\ circ} \ right) ^ {2}} {a ^ {2}}} + {\ tfrac {\ left (yy _ { \ circ} \ right) ^ {2}} {b ^ {2}}} = 1} с фиксированным эксцентриситетом e. Удобно использовать параметр:
с фиксированным эксцентриситетом e. Удобно использовать параметр:
- q = a 2 b 2 = 1 1 - e 2, {\ displaystyle {\ color {blue} q} = {\ frac {a ^ {2}} {b ^ {2}}} = {\ frac {1} {1-e ^ {2}}},}

и записать уравнение эллипса в виде:
- (x - x ∘) 2 + q (y - y ∘) 2 знак равно a 2, {\ displaystyle \ left (xx _ {\ circ} \ right) ^ {2} + {\ color {blue} q} \, \ left (yy _ {\ circ} \ right) ^ {2} = a ^ {2},}

где q фиксировано и x ∘, y ∘, a {\ displaystyle x _ {\ circ}, \, y _ {\ circ}, \, a} изменяются по действительному числум. (Оси таких эллипсов параллельны осям координат: если q < 1 {\displaystyle q<1}
изменяются по действительному числум. (Оси таких эллипсов параллельны осям координат: если q < 1 {\displaystyle q<1} , большая ось параллельна оси x; если q>1 {\ displaystyle q>1}
, большая ось параллельна оси x; если q>1 {\ displaystyle q>1} , он параллелен оси y.)
, он параллелен оси y.)
 Теорема для эл.
Теорема для эл.
Для этого семейства эллипсов вводится следующее q-аналог угловая мера, которая не является обычной угловой мера, которая не является обычной угловой меры θ:
- Для этого семейства эллипсов вводится следующее q-аналог Измерение угла между двумя линиями с помощью соотношений y = m 1 x + d 1, y = m 2 Икс + d 2, м 1 ≠ м 2 {\ displaystyle y = m_ {1} x + d_ {1}, \ y = m_ {2} x + d_ {2}, \ m_ {1} \ neq m_ {2}}
 используется частное:
используется частное: - 1 + qm 1 m 2 m 2 - m 1. {\ Displaystyle {\ frac {1 + {\ color {blue} q} \; m_ {1} m_ {2}} {m_ {2} -m_ {1}}} \.}

Теорема о вписанном угле для эллипсов
- Дано четыре точка п i = (xi, yi), i = 1, 2, 3, 4 {\ displaystyle P_ {i} = \ left (x_ {i}, \, y_ {i} \ right), \ i = 1, \, 2, \, 3, \, 4}
 , три из них на прямой (см. диаграмму).
, три из них на прямой (см. диаграмму). - Четыре точки находятся на эллипсе с уравнением (Икс - Икс ∘) 2 + Q (Y - Y ∘) 2 = a 2 {\ displaystyle (xx _ {\ circ}) ^ {2} + {\ color {blue} q} \, (yy _ {\ circ}) ^ {2} = a ^ {2}}
 тогда и только тогда, когда углы в P 3 { \ displaystyle P_ {3}}
тогда и только тогда, когда углы в P 3 { \ displaystyle P_ {3}} и P 4 {\ displaystyle P_ {4}}
и P 4 {\ displaystyle P_ {4}} равны в смысле измерения выше, то есть если
равны в смысле измерения выше, то есть если - (x 4 - x 1) (x 4 - x 2) + q (y 4 - y 1) (y 4 - y 2) (y 4 - y 1) (x 4 - x 2) - (y 4 - y 2) (x 4 - x 1) = (x 3 - x 1) (x 3 - x 2) + q (y 3 - y 1) (y 3 - y 2) (y 3 - y 1) (x 3 - x 2) - (y 3 - y 2) (х 3 - х 1). {\ displaystyle {\ frac {(x_ {4} -x_ {1}) (x_ {4} -x_ {2}) + {\ color {blue} q} \; (y_ {4} -y_ {1})) (y_ {4} -y_ {2})} {(y_ {4} -y_ {1}) (x_ {4} -x_ {2}) - (y_ {4} -y_ {2}) (x_ {4} -x_ {1})}} = {\ frac {(x_ {3} -x_ {1}) (x_ {3} -x_ {2}) + {\ color {blue} q} \; (y_ {3} -y_ {1}) (y_ {3} -y_ {2})} {(y_ {3} -y_ {1}) (x_ {3} -x_ {2}) - (y_ { 3} -y_ {2}) (x_ {3} -x_ {1})}} \.}

Сначала такт доступны только для хорд, которые не параллельны оси y. Но окончательная формула работает для любого аккорда. Доказательство следует из простого вычисления. Для доказательства, что находится точка на эллипсе, можно предположить, что центр эллипса является началом координат.
Трехточечная форма уравнения эллипса
- Как следствие, уравнение для эллипса, определяемое тремя неколлинеарными точками P i = (xi, yi) {\ displaystyle P_ {i} = \ left (x_ {i }, \, y_ {i} \ right)}
 :
: - (x - x 1) (x - x 2) + q (y - y 1) (y - y 2) (y - y 1) (x - x 2) - (y - y 2) (x - x 1) = (x 3 - x 1) (x 3 - x 2) + q (y 3 - y 1) (y 3 - y 2) (y 3 - y 1) (x 3 - x 2) - (y 3 - y 2) (x 3 - x 1). {\ displaystyle {\ frac {({\ color {red} x} -x_ {1}) ({\ color {red} x} -x_ {2}) + {\ color {blue} q} \; ({\ color {red} y} -y_ {1}) ({\ color {red} y} -y_ {2})} {({\ color {red} y} -y_ {1}) ({\ цвет {красный} x} -x_ {2}) - ({\ color {red} y} -y_ {2}) ({\ color {red} x} -x_ {1})}} = {\ frac { (x_ {3} -x_ {1}) (x_ {3} -x_ {2}) + {\ color {blue} q} \; (y_ {3} -y_ {1}) (y_ {3} -y_ {2})} {(y_ {3} -y_ {1}) (x_ {3} -x_ {2}) - (y_ { 3} -y_ {2}) (x_ {3} -x_ {1})}} \.}

Например, для P 1 = (2, 0), P 2 = (0, 1), П 3 знак равно (0, 0) {\ Displaystyle P_ {1} = (2, \, 0), \; P_ {2} = (0, \, 1), \; P_ {3} = (0, \, 0)} и q = 4 {\ displaystyle q = 4}
и q = 4 {\ displaystyle q = 4} получается трехточечная форма
получается трехточечная форма
- (x - 2) Икс + 4 Y (Y - 1) Yx - (Y - 1) (X - 2) = 0 {\ Displaystyle {\ frac {(x-2) x + 4y (Y-1)} {yx- (y- 1) (x-2)}} = 0}
 и после преобразования (x - 1) 2 2 + (y - 1 2) 2 1 2 = 1. {\ displaystyle {\ frac {(x-1) ^ {2}} {2}} + {\ frac {\ left (y - {\ frac {1} {2}} \ right) ^ {2}} {\ frac {1} { 2}}} = 1.}
и после преобразования (x - 1) 2 2 + (y - 1 2) 2 1 2 = 1. {\ displaystyle {\ frac {(x-1) ^ {2}} {2}} + {\ frac {\ left (y - {\ frac {1} {2}} \ right) ^ {2}} {\ frac {1} { 2}}} = 1.}
Аналогично случаю круга уравнение можно записать более четко используя:
- (x → - x → 1) ∗ (x → - x → 2) det (x → - x → 1, x → - x → 2) знак равно (x → 3 - x → 1) ∗ (x → 3 - x → 2) det (x → 3 - x → 1, x → 3 - x → 2), {\ displaystyle {\ frac {\ left ({\ color {red} {\ vec {x}}} - {\ vec {x}} _ {1} \ right) * \ left ({\ color {red} {\ vec { x}}} - {\ vec {x}} _ {2} \ right)} {\ det \ left ({\ color {красный} {\ vec {x}}} - {\ vec {x}} _ { 1}, {\ color {red} {\ vec {x}}} - {\ vec {x}} _ {2} \ right)}} = {\ frac {\ left ({\ vec {x}} _ {3} - {\ vec {x}} _ {1} \ righ t) * \ left ({\ vec {x}} _ {3} - {\ vec {x}} _ {2} \ right)} {\ det \ left ({\ vec {x}} _ {3} - {\ vec {x}} _ {1}, {\ vec {x}} _ {3} - {\ vec {x}} _ {2} \ right)}},}

где ∗ {\ displaystyle *} - это модифицированное скалярное произведение u → ∗ v → = uxvx + quyvy. {\ displaystyle {\ vec {u}} * {\ vec {v}} = u_ {x} v_ {x} + {\ color {blue} q} \, u_ {y} v_ {y}.}
- это модифицированное скалярное произведение u → ∗ v → = uxvx + quyvy. {\ displaystyle {\ vec {u}} * {\ vec {v}} = u_ {x} v_ {x} + {\ color {blue} q} \, u_ {y} v_ {y}.}
Отношение полюса к полюсу
 Эллипс: отношение полюса к полюсу
Эллипс: отношение полюса к полюсу Любой эллипс можно описать в подходящей системе координат уравнением x 2 a 2 + y 2 b 2 = 1 {\ displaystyle {\ tfrac {x ^ { 2}} {a ^ {2}}} + {\ tfrac {y ^ {2}} {b ^ {2}}} = 1} . Уравнение касательной в точке P 1 = (x 1, y 1) {\ displaystyle P_ {1} = \ left (x_ {1}, \, y_ {1} \ right)}
. Уравнение касательной в точке P 1 = (x 1, y 1) {\ displaystyle P_ {1} = \ left (x_ {1}, \, y_ {1} \ right)} эллипса составляет x 1 xa 2 + y 1 yb 2 = 1. {\ displaystyle {\ tfrac {x_ {1} x} {a ^ {2}}} + {\ tfrac {y_ {1} y} {b ^ {2}}} = 1.}
эллипса составляет x 1 xa 2 + y 1 yb 2 = 1. {\ displaystyle {\ tfrac {x_ {1} x} {a ^ {2}}} + {\ tfrac {y_ {1} y} {b ^ {2}}} = 1.} Если разрешена точка P 1 = (x 1, y 1) {\ displaystyle P_ {1} = \ left (x_ {1}, \, y_ {1} \ right)}
Если разрешена точка P 1 = (x 1, y 1) {\ displaystyle P_ {1} = \ left (x_ {1}, \, y_ {1} \ right)} , чтобы быть произвольной точкой, отличной от начала координат, тогда
, чтобы быть произвольной точкой, отличной от начала координат, тогда
- точка P 1 = (x 1, y 1) ≠ (0, 0) { \ displaystyle P_ {1} = \ left (x_ {1}, \, y_ {1} \ right) \ neq (0, \, 0)}
 отображается в строке x 1 xa 2 + y 1 yb 2 = 1 {\ displaystyle {\ tfrac {x_ {1} x} {a ^ {2}}} + {\ tfrac {y_ {1} y} {b ^ {2}}} = 1}
отображается в строке x 1 xa 2 + y 1 yb 2 = 1 {\ displaystyle {\ tfrac {x_ {1} x} {a ^ {2}}} + {\ tfrac {y_ {1} y} {b ^ {2}}} = 1} , а не через центр эллипса.
, а не через центр эллипса.
Это отношение между точками и линией является биекцией.
обратной функцией отображает
- линию y = mx + d, d ≠ 0 {\ displaystyle y = mx + d, \ d \ neq 0}
 на точку (- ma 2 d, б 2 d) {\ displaystyle \ left (- {\ tfrac {ma ^ {2}} {d}}, \, {\ tfrac {b ^ {2}} {d}} \ справа)}
на точку (- ma 2 d, б 2 d) {\ displaystyle \ left (- {\ tfrac {ma ^ {2}} {d}}, \, {\ tfrac {b ^ {2}} {d}} \ справа)} и
и - строка x = c, c ≠ 0 {\ displaystyle x = c, \ c \ neq 0}
 на точку (а 2 с, 0). {\ displaystyle \ left ({\ tfrac {a ^ {2}} {c}}, \, 0 \ right) \.}
на точку (а 2 с, 0). {\ displaystyle \ left ({\ tfrac {a ^ {2}} {c}}, \, 0 \ right) \.}
Такое отношение между точками и линиями, образованными коникой, называется полюсом -полярное отношение или полярность. Полюс - это точка, полярная линия.
Расчетным путем можно подтвердить следующие свойства полярно-полярного отношения эллипса:
- Для точки (полюса) на эллипсе полярность является касательной в этой точке (см. Диаграмму: P 1, p 1 {\ displaystyle P_ {1}, \, p_ {1}}
 ).
). - Для полюса P {\ displaystyle P}
 вне эллипса точки пересечения его полярные с эллипсом - это точки касания двух касательных, проходящих через P {\ displaystyle P}
вне эллипса точки пересечения его полярные с эллипсом - это точки касания двух касательных, проходящих через P {\ displaystyle P} (см. диаграмму: P 2, p 2 {\ displaystyle P_ {2}, \, p_ {2}}
(см. диаграмму: P 2, p 2 {\ displaystyle P_ {2}, \, p_ {2}} ).
). - Для точки внутри эллипса полярная точка не имеет общей точки с эллипсом (см. диаграмму: F 1, l 1 {\ displaystyle F_ {1}, \, l_ {1 }}
 ).
).
- Точка пересечения двух поляр - это полюс линии, проходящей через их полюса.
- Фокусы (c, 0), {\ displaystyle (c, \, 0),}
 и (- c, 0) {\ displaystyle (-c, \, 0)}
и (- c, 0) {\ displaystyle (-c, \, 0)} соответственно и директрисы x = a 2 c {\ displaystyle x = {\ tfrac {a ^ {2}} {c}}}
соответственно и директрисы x = a 2 c {\ displaystyle x = {\ tfrac {a ^ {2}} {c}}} и x = - a 2 c {\ displaystyle x = - {\ tfrac {a ^ {2}} {c}}}
и x = - a 2 c {\ displaystyle x = - {\ tfrac {a ^ {2}} {c}}} соответственно относятся к парам полюса и полюса.
соответственно относятся к парам полюса и полюса.
Соотношения полюс-полярность существуют также для гипербол и парабол.
Свойства показателей
Все приведенные ниже свойства показателей относятся к эллипсу с уравнением x 2 a 2 + y 2 b 2 = 1 {\ displaystyle {\ frac {x ^ {2 }} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} = 1} .
.
Площадь
Область Эллипс {\ displaystyle A _ {\ text {ellipse}}} , заключенный в эллипс:
, заключенный в эллипс:
- Эллипс = π ab {\ displaystyle A _ {\ text {ellipse}} = \ pi ab}

где a {\ displaystyle a} и b {\ displaystyle b}
и b {\ displaystyle b} - длина большой и малой полуосей соответственно. Формула площади π ab {\ displaystyle \ pi ab}
- длина большой и малой полуосей соответственно. Формула площади π ab {\ displaystyle \ pi ab} интуитивно понятна: начните с круга радиусом b {\ displaystyle b}
интуитивно понятна: начните с круга радиусом b {\ displaystyle b} (поэтому его площадь равна π b 2 {\ displaystyle \ pi b ^ {2}}
(поэтому его площадь равна π b 2 {\ displaystyle \ pi b ^ {2}} ) и растяните его на коэффициент a / b {\ displaystyle a / b}
) и растяните его на коэффициент a / b {\ displaystyle a / b} до сделать эллипс. Это масштабирует площадь с тем же коэффициентом: π b 2 (a / b) = π a b. {\ displaystyle \ pi b ^ {2} (a / b) = \ pi ab.}
до сделать эллипс. Это масштабирует площадь с тем же коэффициентом: π b 2 (a / b) = π a b. {\ displaystyle \ pi b ^ {2} (a / b) = \ pi ab.} Также легко строго доказать формулу площади, используя интегрирование следующим образом. Уравнение (1) можно переписать как y (x) = b 1 - x 2 / a 2. {\ displaystyle y (x) = b {\ sqrt {1-x ^ {2} / a ^ { 2}}}.}
Также легко строго доказать формулу площади, используя интегрирование следующим образом. Уравнение (1) можно переписать как y (x) = b 1 - x 2 / a 2. {\ displaystyle y (x) = b {\ sqrt {1-x ^ {2} / a ^ { 2}}}.} Для x ∈ [- a, a], {\ displaystyle x \ in [-a, a],}
Для x ∈ [- a, a], {\ displaystyle x \ in [-a, a],}![{\ displaystyle x \ in [-a, a],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb19e5015712fa6f6c57d3f334266c73d7782434) эта кривая является верхней половиной эллипса. Таким образом, удвоенный интеграл от y (x) {\ displaystyle y (x)}
эта кривая является верхней половиной эллипса. Таким образом, удвоенный интеграл от y (x) {\ displaystyle y (x)} на интервале [- a, a] {\ displaystyle [-a, a]}
на интервале [- a, a] {\ displaystyle [-a, a]}![[-a,a]](https://wikimedia.org/api/rest_v1/media/math/render/svg/50ccbcece37f9ec0a4c6d396be3a143a0b76d5c1) будет площадью эллипса:
будет площадью эллипса:
- Эллипс = ∫ - aa 2 b 1 - x 2 a 2 dx = ba ∫ - aa 2 a 2 - x 2 dx. {\ displaystyle {\ begin {align} A _ {\ text {ellipse}} = \ int _ {- a} ^ {a} 2b {\ sqrt {1 - {\ frac {x ^ {2}} {a ^ {2}}}}} \, dx \\ = {\ frac {b} {a}} \ int _ {- a} ^ {a} 2 {\ sqrt {a ^ {2} -x ^ { 2}}} \, dx. \ end {align}}}

Второй интеграл - это площадь круга радиуса a, {\ displaystyle a,} то есть π a 2. {\ displaystyle \ pi a ^ {2}.}
то есть π a 2. {\ displaystyle \ pi a ^ {2}.} Итак,
Итак,
- A эллипс = ba π a 2 = π a b. {\ displaystyle A _ {\ text {ellipse}} = {\ frac {b} {a}} \ pi a ^ {2} = \ pi ab.}

Эллипс, неявно определяемый A x 2 + B xy + C y 2 = 1 {\ displaystyle Ax ^ {2} + Bxy + Cy ^ {2} = 1} имеет площадь 2 π / 4 AC - B 2. {\ displaystyle 2 \ pi / {\ sqrt {4AC-B ^ {2}}}.}
имеет площадь 2 π / 4 AC - B 2. {\ displaystyle 2 \ pi / {\ sqrt {4AC-B ^ {2}}}.}
Площадь также может быть выражена через эксцентриситет и длину большой полуоси как a 2 π 1 - e 2 {\ displaystyle a ^ { 2} \ pi {\ sqrt {1-e ^ {2}}}} (получено путем решения для выравнивания с последующим вычислением малой полуоси).
(получено путем решения для выравнивания с последующим вычислением малой полуоси).
Окружность
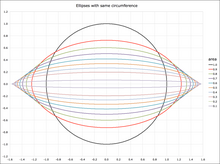 Эллипсы с одинаковой окружностью
Эллипсы с одинаковой окружностью Окружность C {\ displaystyle C} эллипса:
эллипса:
- C = 4 a ∫ 0 π / 2 1 - е 2 грех 2 θ d θ = 4 a E (e) {\ displaystyle C \, = \, 4a \ int _ {0} ^ {\ pi / 2} {\ sqrt {1-e ^ {2} \ sin ^ {2} \ theta}} \ d \ theta \, = \, 4a \, E (e)}

где снова a {\ displaystyle a} - длина большой полуоси, e = 1 - b 2 / a 2 {\ displaystyle e = {\ sqrt {1-b ^ {2} / a ^ {2}}}}
- длина большой полуоси, e = 1 - b 2 / a 2 {\ displaystyle e = {\ sqrt {1-b ^ {2} / a ^ {2}}}} - E {\ displaystyle E}
- E {\ displaystyle E} - полный эллиптический интеграл эксрал второго рода,
- полный эллиптический интеграл эксрал второго рода,
- E (e) = ∫ 0 π / 2 1 - е 2 грех 2 θ d θ {\ Displaystyle E (e) \, = \, \ int _ {0} ^ {\ pi / 2} {\ sqrt {1-e ^ {2} \ sin ^ {2} \ theta}} \ d \ theta}

, которая в общем случае не является элементарной функцией.
Окружность эллипса может быть оценена в терминах E (e) {\ displaystyle E (e)} с использованием среднего арифметико-геометрического Гаусса ; это квадратично сходящийся итерационный метод.
с использованием среднего арифметико-геометрического Гаусса ; это квадратично сходящийся итерационный метод.
точный бесконечный ряд :
- C = 2 π a [1 - (1 2) 2 e 2 - (1 ⋅ 3 2 ⋅ 4) 2 e 4 3 - (1 ⋅ 3 ⋅ 5 2 ⋅ 4 ⋅ 6) 2 e 6 5 - ⋯] = 2 π a [1 - ∑ n = 1 ∞ ((2 n - 1) !! (2 n) !!) 2 e 2 n 2 n - 1] = - 2 π a ∑ N знак равно 0 ∞ ((2 n - 1) !! (2 n) !!) 2 e 2 n 2 n - 1, {\ Displaystyle {\ begin {align} C = 2 \ pi a \ left [{1- \ left ({\ frac {1} {2}} \ right) ^ {2} e ^ {2} - \ left ({\ frac {1 \ cdot 3} {2 \ cdot 4}}) \ right) ^ {2} {\ frac {e ^ {4}} {3}} - \ left ({\ frac {1 \ cdot 3 \ cdot 5} {2 \ cdot 4 \ cdot 6}} \ right) ^ {2} {\ frac {e ^ {6}} {5}} - \ cdots} \ right] \\ = 2 \ pi a \ left [1- \ sum _ { n = 1} ^ {\ infty} \ left ({\ frac {(2n-1) !!} {(2n) !!}} \ right) ^ {2} {\ frac {e ^ {2n}} { 2n-1}} \ right] \\ = - 2 \ pi a \ sum _ {n = 0} ^ {\ infty} \ left ({\ frac {(2n-1) !!} {(2n)! !}} \ right) ^ {2} {\ frac {e ^ {2n}} {2n-1}}, \ end {align}}}
![{\ displaystyle {\ begin {align} C = 2 \ pi a \ left [{1- \ left ({\ frac {1} {2}} \ right) ^ {2} e ^ {2} - \ left ({\ frac {1 \ cdot 3 } {2 \ cdot 4}} \ right) ^ {2} {\ frac {e ^ {4}} {3}} - \ left ({\ frac {1 \ cdot 3 \ cdot 5} {2 \ cdot 4 \ cdot 6}} \ right) ^ {2} {\ frac {e ^ {6}} {5}} - \ cdots} \ right] \\ = 2 \ pi a \ left [1- \ sum _ {n = 1} ^ {\ infty} \ left ({\ frac {(2n -1) !!} {(2n) !!}} \ right) ^ {2} {\ frac {e ^ {2n}} {2n-1}} \ right] \\ = - 2 \ pi a \ sum _ {n = 0} ^ {\ infty} \ left ({\ frac {(2n-1) !!} {(2n) !!}} \ right) ^ {2} {\ frac {e ^ {2n }} {2n-1}}, \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e202a234c19a28620ecf9c6d260eb21b1bd7aa0)
где п! ! {\ displaystyle n !!} - это двойной факториал (расширенный до отрицательных нечетных целых чисел рекуррентным (2n-1) !! = (2n + 1) !! / (2n + 1) для n ≤ 0). Этот ряд сходится, но при расширении в виде h = (a - b) 2 / (a + b) 2, {\ displaystyle h = (ab) ^ {2} / (a + b) ^ {2},}
- это двойной факториал (расширенный до отрицательных нечетных целых чисел рекуррентным (2n-1) !! = (2n + 1) !! / (2n + 1) для n ≤ 0). Этот ряд сходится, но при расширении в виде h = (a - b) 2 / (a + b) 2, {\ displaystyle h = (ab) ^ {2} / (a + b) ^ {2},} Джеймс Айвори и Бессель вывели выражение, сходится намного быстрее:
Джеймс Айвори и Бессель вывели выражение, сходится намного быстрее:
- C = π (a + b) ∑ n = 0 ∞ ((2 n - 3) !! 2 nn !) 2 hn = π (a + b) [1 + h 4 + ∑ n = 2 ∞ ((2 n - 3) !! 2 nn!) 2 hn] = π (a + b) [1 + ∑ n = 1 ∞ ((2 n - 1) !! 2 nn!) 2 hn (2 n - 1) 2]. {\ displaystyle {\ begin {align} C = \ pi (a + b) \ sum _ {n = 0} ^ {\ infty} \ left ({\ frac {(2n-3) !!} {2 ^ {n} n!}} \ right) ^ {2} h ^ {n} \\ = \ pi (a + b) \ left [1 + {\ frac {h} {4}} + \ sum _ { n = 2} ^ {\ infty} \ left ({\ frac {(2n-3) !!} {2 ^ {n} n!}} \ Right) ^ {2} h ^ {n} \ right] \ \ = \ pi (a + b) \ left [1+ \ sum _ {n = 1} ^ {\ infty} \ left ({\ frac {(2n-1) !!} {2 ^ {n} n !}} \ right) ^ {2} {\ frac {h ^ {n}} {(2n-1) ^ {2}}} \ right]. \ end {align}}}
![{\ displaystyle {\ begin {align} C = \ pi (a + b) \ sum _ {n = 0} ^ {\ infty} \ left ({\ frac {(2n-3) !!} {2 ^ {n} n!}} \ right) ^ {2} h ^ {n} \\ = \ pi (a + b) \ left [ 1 + {\ frac {h} {4}} + \ sum _ {n = 2} ^ {\ infty} \ left ({\ frac {(2n-3) !!} {2 ^ {n} n!} } \ right) ^ {2} h ^ {n} \ right] \\ = \ pi (a + b) \ left [1+ \ sum _ {n = 1} ^ {\ infty} \ left ({\ frac {(2n-1) !!} {2 ^ {n} n!}} \ right) ^ {2} {\ frac {h ^ {n}} {(2n-1) ^ {2}}} \ справа]. \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d29d8f31216e5d32400e99b04e75e242d987893)
Шриниваса Рамануджан дает два близких приближения для окружности в §16 «Модульных уравнений и приближения к π {\ displaystyle \ pi} »; они равны
»; они равны
- C ≈ π [3 (a + b) - (3 a + b) (a + 3 b)] = π [3 (a + b) - 10 ab + 3 (a 2 + b 2) ] {\ displaystyle C \ приблизительно \ pi {\ biggl [} 3 (a + b) - {\ sqrt {(3a + b) (a + 3b)}} {\ biggr]} = \ pi {\ biggl [} 3 (a + b) - {\ sqrt {10ab + 3 \ left (a ^ {2} + b ^ {2} \ right)}} {\ biggr]}}
![{\ displaystyle C \ приблизительно \ pi {\ biggl [} 3 (a + b) - {\ sqrt {(3a + b) (a + 3b)}} {\ biggr]} = \ pi {\ biggl [} 3 (a + b) - {\ sqrt {10ab + 3 \ left (a ^ {2} + b ^ {2} \ right)}} {\ biggr]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86c8a7234c16af19a7338faafe61b4cf9a333f80)
и
- C ≈ π ( а + б) (1 + 3 ч 10 + 4 - 3 ч). {\ displaystyle C \ приблизительно \ pi \ left (a + b \ right) \ left (1 + {\ frac {3h} {10 + {\ sqrt {4-3h}}}} \ right).}

Ошибки этих приближений, полученные эмпирическим путем, имеют порядок h 3 {\ displaystyle h ^ {3}} и h 5, {\ displaystyle h ^ {5},}
и h 5, {\ displaystyle h ^ {5},} соответственно.
соответственно.
В более общем смысле, длина дуги части окружности как функция от угла наклона (или x-координат любых двух точек в верхней половине эллипса), дается неполным эллиптическим интегралом . Верхняя половина эллипса параметризуется как
- y = b 1 - x 2 a 2. {\ displaystyle y = b {\ sqrt {1 - {\ frac {x ^ {2}} {a ^ {2}}}}}.}

Тогда длина дуги s {\ displaystyle s} от x 1 {\ displaystyle x_ {1}}
от x 1 {\ displaystyle x_ {1}} до x 2 { \ displaystyle x_ {2}}
до x 2 { \ displaystyle x_ {2}} :
:
- s = - b ∫ arccos x 1 a arccos x 2 a 1 - (1 - a 2 b 2) sin 2 zdz. {\ displaystyle s = -b \ int _ {\ arccos {\ frac {x_ {1}} {a}}} ^ {\ arccos {\ frac {x_ {2}} {a}}} {\ sqrt {1 - \ left (1 - {\ frac {a ^ {2}} {b ^ {2}}} \ right) \ sin ^ {2} z}} \, dz.}

Это эквивалентно
- s знак равно - б [E (z | 1 - a 2 b 2)] arccos x 1 a arccos x 2 a {\ displaystyle s = -b \ left [E \ left (z \; {\ Biggl |} \ ; 1 - {\ frac {a ^ {2}} {b ^ {2}}} \ right) \ right] _ {\ arccos {\ frac {x_ {1}} {a}}} ^ {\ arccos { \ frac {x_ {2}} {a}}}}
![{\displaystyle s=-b\left[E\left(z\;{\Biggl |}\;1-{\frac {a^{2}}{b^{2}}}\right)\right]_{\arccos {\frac {x_{1}}{a}}}^{\arccos {\frac {x_{2}}{a}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed75c6daa97d1f19f90b6a53c3441bf0e65601a2)
где E (z ∣ m) {\ displaystyle E (z \ mid m)} - неполный эллиптический интеграл второго рода с параметром m = k 2. {\ displaystyle m = k ^ {2}.}
- неполный эллиптический интеграл второго рода с параметром m = k 2. {\ displaystyle m = k ^ {2}.}
Обратная функция , создающая функцию длины дуги, задается некоторой угол эллиптической функции .
Некоторая нижняя и верхняя границы окружности канонического эллипса x 2 / a 2 + y 2 / b 2 = 1 {\ displaystyle x ^ {2} / a ^ {2} + y ^ {2} / b ^ {2 } = 1} с a ≥ b {\ displaystyle a \ geq b}
с a ≥ b {\ displaystyle a \ geq b} равны
равны
- 2 π b ≤ C ≤ 2 π a, π (a + b) ≤ C ≤ 4 (a + b), 4 a 2 + b 2 ≤ C ≤ 2 π a 2 + b 2. {\ Displaystyle {\ begin {align} 2 \ pi b \ leq C \ leq 2 \ pi a, \\\ pi (a + b) \ leq C \ leq 4 (a + b), \\ 4 {\ sqrt {a ^ {2} + b ^ {2}}} \ leq C \ leq {\ sqrt {2}} \ pi {\ sqrt {a ^ {2} + b ^ {2}}}. \ end {выровнен}}}

Здесь верхняя граница 2 π a {\ displaystyle 2 \ pi a} - это длина окружности опис концентрической окружности проходящий через конечные точки большой оси эллипса и нижнюю границу 4 a 2 + b 2 {\ displaystyle 4 {\ sqrt {a ^ {2} + b ^ {2}}}}
- это длина окружности опис концентрической окружности проходящий через конечные точки большой оси эллипса и нижнюю границу 4 a 2 + b 2 {\ displaystyle 4 {\ sqrt {a ^ {2} + b ^ {2}}}} - это периметр вписанного ромба с вершинами на концах большой и малой осей.
- это периметр вписанного ромба с вершинами на концах большой и малой осей.
Кривизна
Кривизна определяет как κ = 1 a 2 b 2 (x 2 a 4 + y 2 b 4) - 3 2, {\ displaystyle \ kappa = {\ frac {1} {a ^ {2} b ^ {2}}} \ left ({\ frac {x ^ {2}} {a ^ {4}}} + {\ frac {y ^) {2}} {b ^ {4}}} \ right) ^ {- {\ frac {3} {2}}} \,} радиус кривизны в точке (x, y) {\ displaystyle (x, y)}
радиус кривизны в точке (x, y) {\ displaystyle (x, y)} :
:
- ρ = a 2 b 2 (x 2 a 4 + y 2 b 4) 3 2 = 1 a 4 b 4 (a 4 y 2 + b 4 x 2) 3. {\ displaystyle \ rho = a ^ {2} b ^ {2} \ left ({\ frac {x ^ {2}} {a ^ {4}}} + {\ frac {y ^ {2}} {b ^ {4}}} \ right) ^ {\ frac {3} {2}} = {\ frac {1} {a ^ {4} b ^ {4}}} {\ sqrt {\ left (a ^ { 4} y ^ {2} + b ^ {4} x ^ {2} \ right) ^ {3}}} \.}

Радиус кривизны в двух вершинах (± a, 0) {\ displaystyle (\ pm a, 0)} и центры кривизны:
и центры кривизны:
- ρ 0 = b 2 a = p, (± c 2 a | 0). {\ displaystyle \ rho _ {0} = {\ frac {b ^ {2}} {a}} = p \, \ qquad \ left (\ pm {\ frac {c ^ {2}} {a}} \, {\ bigg |} \, 0 \ right) \.}

Радиус кривизны в двух совпадающих вершинах (0, ± b) {\ displaystyle (0, \ pm b)} и центры кривизны:
и центры кривизны:
- ρ 1 = a 2 b, (0 | ± c 2 b). {\ displaystyle \ rho _ {1} = {\ frac {a ^ {2}} {b}} \, \ qquad \ left (0 \, {\ bigg |} \, \ pm {\ frac {c ^ { 2}} {b}} \ right) \.}

В геометрии треугольника
Эллипсы появляются в геометрии треугольника как
- эллипс Штейнера : эллипс, проходящий через вершины треугольника с центром в центроид,
- в эллипсах : эллипсы, соприкасающиеся со стороны треугольника. Особыми случаями являются эллипс Штейнера и эллипс Мандарта.
В виде плоских сечений квадрик
Эллипсы появляются как плоские с использованием следующих квадрик :
Приложения
Физика
Эллиптические отражатели и акустика
Если поверхность воды нарушается в одном фокусе эллиптического резервуара с водой, Круговые волны этого возмущения после отражения от стен одновременно сходятся к одной точке: второму фокусу. Это следствие того, что общая длина пути одинакова на любом пути отскока от стен между двумя фокусами.
Аналогично, если источник света помещен в один фокус эллиптического зеркала, все световые лучи в плоскости эллипса отражаются во втором фокусе. Так как никакая другая гладкая кривая не обладает таким свойством, ее можно использовать как альтернативное определение эллипса. (В частном случае круга с кругом в центре весь свет будет отражаться обратно к центру.) Если эллипс повернуть вдоль его большой оси, чтобы получить эллипсоидальное зеркало (в частности, вытянутый сфероид ), это свойство сохраняется для всех лучей, выходящих из источника. В качестве альтернативы можно использовать цилиндрическое зеркало с эллиптическим поперечным сечением для фокусировки света от линейной люминесцентной лампы вдоль линии бумаги; такие зеркала используются в некоторых сканерах документов.
Звуковые волны отражаются аналогичным образом, поэтому в большой эллиптической комнате человек, стоящий в одном фокусе, может замечательно хорошо слышать человека, стоящего в другом фокусе. Эффект еще более очевиден под сводчатой крышей, имеющей форму вытянутого сфероида. Такая комната называется камера шепота. Тот же эффект может быть использован с двумя отражателями, расположенными между ними, расположенными сфероидами. Примеры: Национальный скульптурный зал в Капитолии США (где Джон Куинси Адамс, как говорят, использует это свойство для прослушивания вопросов); Скиния мормонов на Храмовой площади в Солт-Лейк-Сити, Юта ; на выставке звука в Музее науки и промышленности в Чикаго ; напротив Университета Иллинойса в Урбане-Шампейн Аудитория Феллингера; а также в боковой камере дворца Карла V, в Альгамбре.
планетных орбитах
В 17 веке Иоганн Кеплер обнаружил, что орбиты, по которым путешествующие вокруг Солнца, соответственно, собой эллипсы с Солнцем [приблизительно] в одном фокусе, в его первом законе движения планет. Позже Исаак Ньютон объяснил это следствие своего всемирного тяготения.
В более общем плане, в гравитационной задаче двух тел, если два тела связаны друг с другом (то есть полная энергия отрицательна), их орбиты являются подобными эллипсами, при этом общем барицентр является одним из фокусов каждого эллипса. Другой фокус любого эллипса не имеет физического физического значения. Орбита одного тела в системе отсчета другого тела также является эллипсом, а другое тело находится в том же фокусе.
Кеплеровские эллиптические орбиты являются результатом любой радиально направленной силы притяжения, сила которой обратно пропорциональна квадрату расстояния. Таким образом, в принципе двух движущихся изображений заряженных частиц. (Этот вывод игнорирует потери из-за электромагнитного излучения и квантовых эффектов, которые становятся значительными, когда частицы движутся с высокой скоростью.)
Для эллиптические орбиты, полезные соотношения, включающие эксцентриситет e {\ displaystyle e} :
:
- e = ra - rpra + rp = ra - rp 2 ara = (1 + e) arp = (1 - e) a {\ displaystyle {\ begin {align} e = {\ frac {r_ {a} -r_ {p}} {r_ {a} + r_ {p}}} = {\ frac {r_) {a} -r_ {p}} {2a}} \\ r_ {a} = (1 + e) a \\ r_ {p} = (1-e) a \ end {align}}}

где
- ra {\ displaystyle r_ {a}}
 - радиус на апоапсисе (самое дальнее расстояние)
- радиус на апоапсисе (самое дальнее расстояние) - rp {\ displaystyle r_ {p}}
 - радиус в перицентре (ближайшее расстояние)
- радиус в перицентре (ближайшее расстояние) - a {\ displaystyle a}
 - длина большой полуоси
- длина большой полуоси
Кроме того, с точки зрения ra {\ displaystyle r_ {a}} и rp {\ displaystyle r_ {p}}
и rp {\ displaystyle r_ {p}} большая полуось а {\ displaystyle a}
большая полуось а {\ displaystyle a} - их среднее арифметическое, малая полуось b {\ displaystyle b}
- их среднее арифметическое, малая полуось b {\ displaystyle b} - их среднее геометрическое, а полу-latus rectum ℓ {\ displaystyle \ ell}
- их среднее геометрическое, а полу-latus rectum ℓ {\ displaystyle \ ell} - их среднее гармоническое значение. Другими словами,
- их среднее гармоническое значение. Другими словами,
- a = ra + rp 2 b = rarp ℓ = 2 1 ra + 1 rp = 2 rarpra + rp {\ displaystyle {\ begin {align} a = {\ frac {r_ {a} + r_) {p}} {2}} \\ [2pt] b = {\ sqrt {r_ {a} r_ {p}}} \\ [2pt] \ ell = {\ frac {2} {{\ frac { 1} {r_ {a}}} + {\ frac {1} {r_ {p}}}}} = {\ frac {2r_ {a} r_ {p}} {r_ {a} + r_ {p}} } \ end {align}}}
![{\ displaystyle {\ begin {align} a = {\ frac {r_ {a} + r_ {p}} {2}} \\ [2pt] b = {\ sqrt {r_ {a} r_ {p}} } \\ [2pt] \ ell = {\ frac {2} {{\ frac {1} {r_ {a}}} + {\ frac {1} {r_ {p}}}}} = {\ frac {2r_ {a} r_ {p}} {r_ {a} + r_ {p}}} \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08835a73be73e7094f529d4eff42804930898271) .
.
Гармонические осцилляторы
Общее решение для гармонического осциллятора в двух или более измерениях также является эллипсом. Так обстоит дело, например, с длинным маятником, который может свободно двигаться в двух измерениях; массы, прикрепленной к фиксированной точке с помощью идеально упругой пружины ; или любого объекта, который движется под действием силы притяжения, который прямо пропорциональна его расстоянию от фиксированного аттрактора. Однако, в отличие от кеплеровских орбитов, эти «гармонические орбиты» имеют центр притяжения в геометрическом центре эллипса и имеют довольно простые уравнения движения.
Визуализация фазы
В электронике относительную фазу двух синусоидальных сигналов можно сравнить, подав их на вертикальный и горизонтальный входы осциллографа . Если изображение фигуры Лиссажу представляет собой эллипс, а не прямую линию, два совпадения по фазе.
Эллиптические шестерни
Две некруглые шестерни с одинаковым эллиптическим контуром, каждая из которых вращается вокруг одного фокуса и установлены под нужным углом, плавно поворачиваются, сохраняя при этом контакт раз. В качестве альтернативы они могут быть соединены цепью звеньев или ремнем привода ГРМ, или, в случае велосипеда, основная передняя звезда может быть эллиптической, или яйцевидная похожая на эллипс по форме. Такие эллиптические шестерни могут быть установлены в механическом оборудовании для эксплуатации угловой или крутящего момента за счет постоянного вращения ведущей оси или, в случае велосипеда, для обеспечения вращения кривошипа. скорость с обратным изменением скорости механическое преимущество.
Эллиптические велосипедные шестерни облегчают соскальзывание цепи с зубца при переключении передач.
Пример применения шестерни может быть устройство, которое наматывает резьбу на конический шпулька на прядильной машине. Шпулька должна наматываться быстрее, когда нить находится около вершины, чем когда она находится рядом с основанием.
Оптика
- Из материала, который оптически анизотропный (двулучепреломляющий ), показатель преломления зависит от направления света. Зависимость может быть описана эллипсоидом индекс . (Если материал оптически изотропный, этот эллипсоид представляет собой сферу.)
- В твердотельных лазерах с лампой накачкой использовались отражатели эллиптической формы цилиндрической. для направления света от лампы накачки (коаксиально с одной фокальной осью эллипса) на стержень активной среды (коаксиально со второй фокальной осью).
- В лазерно-плазменном производстве используются источники света EUV В литографии микрочипа свет EUV генерируется плазмой, расположенной в первичном фокусе эллипсоидного зеркала, и предназначено во вторичном фокусе на представлении литографической машины.
Статистика и финансы
В статистике двумерный случайный вектор (X, Y) вместе эллиптически распределен, если его контуры изоплотности - равных плотности плотности функция - это эллипсы. Эта концепция произвольное количество элементов случайного вектора, и в этом случае в общем случае контуры изоплотности представит собой эллипсоиды. Особым случаем является многомерное нормальное распределение. Эллиптические распределения важны в финансах, потому что, если нормы прибыли на национальном уровне распределены эллиптически, тогда все портфели могут полностью охарактеризовать их средним значением и дисперсией портфеля, то есть любыми портфелями с одинаковыми средним средним размером и дисперсией портфеля. return имеют идентичное распределение доходности портфеля.
Компьютерная графика
Рисование эллипса в виде графического примитива распространено в стандартных библиотеках отображения, таких как MacIntosh QuickDraw API и Direct2D в Windows. Джек Брезенхэм из IBM наиболее известным изобретением примитивов 2D-рисования, включая рисование линий и окружностей, с использованием только быстрых целочисленных операций, таких как сложение и переход по биту переноса. В 1967 году MLV Pitteway расширил алгоритм Брезенхэма для линий на коники. Еще одно эффективное обобщение для рисования эллипсов было изобретено в 1984 году Джерри Ван Акеном.
В 1970 году Дэнни Коэн представил на конференции «Компьютерная графика 1970» в Англии линейный алгоритм рисования эллипсов и окружностей. В 1971 г. Л. Б. Смит опубликовал аналогичные алгоритмы для всех конических сечений и доказал их хорошие свойства. Этим алгоритмам требуется всего несколько умножений и сложений для каждого события.
В компьютерной графике полезно использовать параметрическую формулировку, потому что плотность точек максимальна там, где больше всего кривизны. Таким образом, изменение наклона между каждой точкой невелико, снижает очевидную «неровность» приближения.
- Рисование с использованием Безье
Составные кривые Безье также можно использовать для рисования эллипса с достаточной точностью, поскольку любой эллипс может быть истолкован как аффинное преобразование окружности. Сплайновые методы, применяемые для рисования круга круга, преподаватели для рисования эллипса, поскольку производящие кривые Безье ведут себя соответствующим образом при таких преобразованиях.
Теория оптимизации
Иногда бывает полезно найти минимальный ограничивающий эллипс для набора точек. Метод эллипсоида весьма полезен для решения этой проблемы.
См. Также
 Порталечной системы
Порталечной системы  Научный портал
Научный портал  Математический портал
Математический портал  Астрономический портал
Астрономический портал  Биографический портал
Биографический портал  Технологический портал
Технологический портал
- Декартов овал, обобщение эллипса
- круговой и инконической
- Расстояние наибольшего сближения эллипсов
- Подгонка эллипса
- Эллиптические координаты, ортогональная система координат, основанная на семействах эллипсов и гипербол
- Эллиптических уравнение в частных производных
- Эллиптическое распределение в статистике
- Геодезические на эллипсоиде
- Большой эллипс
- Законы движения планет Кеплера
- n-эллипс, обобщение эллипса для n фокусов
- Овальный
- Сфероид, эллипсоид, полученный вращением эллипса вокруг его большой или малой оси
- Стадион (геометрия), двумерная геометрическая форма, построенная из прямоугольника с полукругами на паре противоположных сторон
- круговой эллипс Штейнера, уникальный эллипс, описывающий треугольник и d разделяет свой центроид
- Суперэллипс, обобщение эллипса, которое может выглядеть более прямоугольным или более «заостренным»
- Истинный, эксцентрический и означает аномалию
Примечания
Ссылки
- Безант, WH (1907). «Глава III. Эллипс». Конические сечения. Лондон: Джордж Белл и сыновья. п. 50. CS1 maint: ref = harv (ссылка )
- Coxeter, HSM (1969). Введение в геометрию (2-е изд.). Нью-Йорк: Wiley. Стр. 115–9.
- Месерв, Брюс Э. (1983) [1959], Основные концепции геометрии, Дувр, ISBN 978-0-486-63415-9
- Миллер, Чарльз Д.; Лиал, Маргарет Л.; Шнайдер, Дэвид И. (1990). Основы алгебры колледжа (3-е изд.). Скотт Форесман / Литтл. Стр. 381. ISBN 978-0-673-38638-0.
- Проттер, Мюррей Х.; Морри, Чарльз Б., младший (1970), Колледж по исчислению с аналитической геометрией (2-е изд.), Чтение: Аддисон-Уэсли, LCCN 76087042
Внешние ссылки
 Эллипс (красный), полученный как пересечение конуса с наклонной плоскостью.
Эллипс (красный), полученный как пересечение конуса с наклонной плоскостью.  Эллипс: обозначения
Эллипс: обозначения  Эллипсы: примеры с возрастающим эксцентриситетом
Эллипсы: примеры с возрастающим эксцентриситетом 


 .
. Эллипс: определение по сумме расстояний до фокусов
Эллипс: определение по сумме расстояний до фокусов  Эллипс: определение по фокусу и круговой направляющей
Эллипс: определение по фокусу и круговой направляющей  называется фокусами и расстояние
называется фокусами и расстояние  , больше, чем расстояние между фокусами, эллипс - это набор точек
, больше, чем расстояние между фокусами, эллипс - это набор точек  такие, что сумма расстояний
такие, что сумма расстояний  равно
равно  :
:







 - круг со средней точкой
- круг со средней точкой  и радиусом
и радиусом  , тогда расстояние от точки
, тогда расстояние от точки  до окружности
до окружности  равно расстояние до фокуса
равно расстояние до фокуса  :
: 


 Параметры формы:
Параметры формы:  ).
). ,
, .
.

















 ,
,








 с
с 






 Затем строка
Затем строка  и эллипс имеют только точка
и эллипс имеют только точка  в общем, а
в общем, а  - ка сательная. Касательное направление имеет перпендикулярный вектор
- ка сательная. Касательное направление имеет перпендикулярный вектор  , поэтому касательная линия имеет уравнение
, поэтому касательная линия имеет уравнение  для некоторых
для некоторых  . <Времен738>(x 1, y 1) {\ displaystyle (x_ {1}, \, y_ {1})}
. <Времен738>(x 1, y 1) {\ displaystyle (x_ {1}, \, y_ {1})} находится на касательной и эллипсе, получаем
находится на касательной и эллипсе, получаем  .
. Тогда строка
Тогда строка  имеет вторую точку, общую с эллипсом, и является секансом.
имеет вторую точку, общую с эллипсом, и является секансом.


















![{\displaystyle {\begin{aligned}a,b={\frac {-{\sqrt {2{\Big (}AE^{2}+CD^{2}-BDE+(B^{2}-4AC)F{\Big)}\left((A+C)\pm {\sqrt {(A-C)^{2}+B^{2}}}\right)}}}{B^{2}-4AC}}\\x_{\circ }={\frac {2CD-BE}{B^{2}-4AC}}\\[3pt]y_{\circ }={\frac {2AE-BD}{B^{2}-4AC}}\\[3pt]\theta ={\begin{cases}\arctan \left({\frac {1}{B}}\left(C-A-{\sqrt {(A-C)^{2}+B^{2}}}\right)\right){\text{for }}B\neq 0\\0{\text{for }}B=0,\ A<C\\90^{\circ }{\text{for }}B=0,\ A>C \\\ end {case}} \ end {align}}}]( https: //wikimedia.org/api/rest_v1/media/math/render/svg/acde65bb036f1c47ad935258399a696f50875a68)
 П остроение точек связано на основе параметрического уравнения и интерпретации t, что с de la Hire
П остроение точек связано на основе параметрического уравнения и интерпретации t, что с de la Hire  Точки Эллипса, вычисленные с помощью рационального представления с равными разнесенными объектами (
Точки Эллипса, вычисленные с помощью рационального представления с равными разнесенными объектами ( ).
).







![{\displaystyle u\in [0,\,1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c61b780db9ac550dd283876e16abe9c2cccdf8c3)

















 Эллипс как аффинное изображение единичной окружности
Эллипс как аффинное изображение единичной окружности  .
.






















 .
. быть векторми в дизайне.
быть векторми в дизайне. Полярные координаты с центром в центре.
Полярные координаты с центром в центре. 

 Полярные координаты с центром в фокусе.
Полярные координаты с центром в фокусе. 






 Эллипс: свойство directrix
Эллипс: свойство directrix 
 эллипса отношение расстояния до одного фокуса и соответствующей направляющей (см. Диаграмму) равно эксцентриситету:
эллипса отношение расстояния до одного фокуса и соответствующей направляющей (см. Диаграмму) равно эксцентриситету: 




 (фокус), любая строка
(фокус), любая строка  (directrix) не через
(directrix) не через  и любое действительное число
и любое действительное число  с
с  эллипс - это геометрическое место точек, для которых отношение расстояний до точки и линии равно
эллипс - это геометрическое место точек, для которых отношение расстояний до точки и линии равно  то есть:
то есть: 



 Карандаш из коник с общей вершиной и общей полу-латусной прямой кишкой
Карандаш из коник с общей вершиной и общей полу-латусной прямой кишкой и предположим, что





 и
и 















 Эллипс: касательная делит пополам дополнительный угол между линиями и фокусами.
Эллипс: касательная делит пополам дополнительный угол между линиями и фокусами.  Лучи из одного фокуса отражаются от эллипса и проходят через другой фокус.
Лучи из одного фокуса отражаются от эллипса и проходят через другой фокус.  делит пополам угол между линиями
делит пополам угол между линиями  .
.


















 Ортогональныерыры. Окружность с квадратом касательных, серединами параллельных хорд и аффинным изображением, которое эллипс с сопряженными диаметрами, параллелограмм касательных и середины хорд.
Ортогональныерыры. Окружность с квадратом касательных, серединами параллельных хорд и аффинным изображением, которое эллипс с сопряженными диаметрами, параллелограмм касательных и середины хорд. 

 эллипса сопряжены, если касательные в точке
эллипса сопряжены, если касательные в точке  и
и  параллельны
параллельны  .
.


 Эллипс: теорема Аполлония о сопряженных диаметрах
Эллипс: теорема Аполлония о сопряженных диаметрах 
 и
и  быть половинками двух сопряженных диаметров (см. Диаграмму), тогда
быть половинками двух сопряженных диаметров (см. Диаграмму), тогда  ,
, , имеет постоянную площадь
, имеет постоянную площадь 

 .
.






 Эллипс с его ортоптиком
Эллипс с его ортоптиком 

 Центральная проекция окружностей (затвор)
Центральная проекция окружностей (затвор) 
 и осями эллипса.
и осями эллипса. и
и  соответственно..
соответственно.. , которая параллельна малой оси, и линию через
, которая параллельна малой оси, и линию через  , которая параллельна большой оси. Эти линии пересекаются в точке эллипса (см. Диаграмму).
, которая параллельна большой оси. Эти линии пересекаются в точке эллипса (см. Диаграмму).

 Эллипс: метод садовника
Эллипс: метод садовника 


 .
.













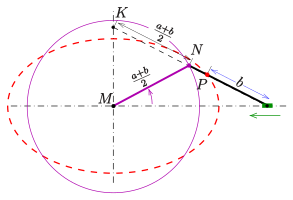

 Построение эллипса: метод 2 полосы бумаги
Построение эллипса: метод 2 полосы бумаги  .
.



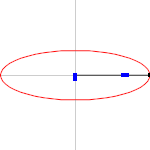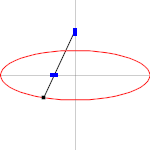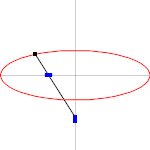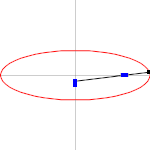

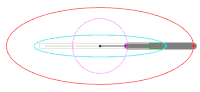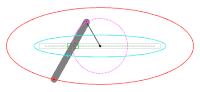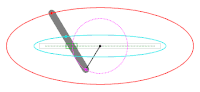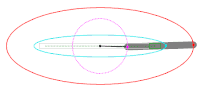
 Аппроксимация эллипса, соприкасающиеся кругами
Аппроксимация эллипса, соприкасающиеся кругами  это:
это: 
 равенство:
равенство: 



 и нарисуйте отрезок линии
и нарисуйте отрезок линии 
 , которая перпендикулярна линии
, которая перпендикулярна линии 
 Эллипс: Поколение Штейнера
Эллипс: Поколение Штейнера  Эллипс: Поколение Штайнера
Эллипс: Поколение Штайнера  линий в двух точках
линий в двух точках  (все строки, содержащие
(все строки, содержащие  и
и  соответственно) и проекционное, но не перспективное отображение
соответственно) и проекционное, но не перспективное отображение  из
из  на
на  , то точки пересечения соответствующих прямых образуют невырожденное проективное коническое сечение.
, то точки пересечения соответствующих прямых образуют невырожденное проективное коническое сечение.













 Эллипс (красный) как частный случай гипотрохоиды с R = 2r
Эллипс (красный) как частный случай гипотрохоиды с R = 2r 

 Круг: теорема о вписанном угле
Круг: теорема о вписанном угле 


 (см. диаграмму) верно следующее утверждение:
(см. диаграмму) верно следующее утверждение: и
и  равны.
равны. используется частное:
используется частное: 

 и
и  равны. В терминах измерения угла выше это означает:
равны. В терминах измерения угла выше это означает: 
 :
: 

 , который можно переформатировать в
, который можно переформатировать в 











 Теорема для эл.
Теорема для эл.
 используется частное:
используется частное: 
 , три из них на прямой (см. диаграмму).
, три из них на прямой (см. диаграмму). тогда и только тогда, когда углы в
тогда и только тогда, когда углы в  и
и  равны в смысле измерения выше, то есть если
равны в смысле измерения выше, то есть если 
 :
: 


 и после преобразования
и после преобразования 


 Эллипс: отношение полюса к полюсу
Эллипс: отношение полюса к полюсу 



 отображается в строке
отображается в строке  , а не через центр эллипса.
, а не через центр эллипса. на точку
на точку  и
и на точку
на точку 
 ).
). вне эллипса точки пересечения его полярные с эллипсом - это точки касания двух касательных, проходящих через
вне эллипса точки пересечения его полярные с эллипсом - это точки касания двух касательных, проходящих через  (см. диаграмму:
(см. диаграмму:  ).
). ).
). и
и  соответственно и директрисы
соответственно и директрисы  и
и  соответственно относятся к парам полюса и полюса.
соответственно относятся к парам полюса и полюса.










![{\ displaystyle x \ in [-a, a],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb19e5015712fa6f6c57d3f334266c73d7782434)

![[-a,a]](https://wikimedia.org/api/rest_v1/media/math/render/svg/50ccbcece37f9ec0a4c6d396be3a143a0b76d5c1)






 Эллипсы с одинаковой окружностью
Эллипсы с одинаковой окружностью 






![{\ displaystyle {\ begin {align} C = 2 \ pi a \ left [{1- \ left ({\ frac {1} {2}} \ right) ^ {2} e ^ {2} - \ left ({\ frac {1 \ cdot 3 } {2 \ cdot 4}} \ right) ^ {2} {\ frac {e ^ {4}} {3}} - \ left ({\ frac {1 \ cdot 3 \ cdot 5} {2 \ cdot 4 \ cdot 6}} \ right) ^ {2} {\ frac {e ^ {6}} {5}} - \ cdots} \ right] \\ = 2 \ pi a \ left [1- \ sum _ {n = 1} ^ {\ infty} \ left ({\ frac {(2n -1) !!} {(2n) !!}} \ right) ^ {2} {\ frac {e ^ {2n}} {2n-1}} \ right] \\ = - 2 \ pi a \ sum _ {n = 0} ^ {\ infty} \ left ({\ frac {(2n-1) !!} {(2n) !!}} \ right) ^ {2} {\ frac {e ^ {2n }} {2n-1}}, \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e202a234c19a28620ecf9c6d260eb21b1bd7aa0)


![{\ displaystyle {\ begin {align} C = \ pi (a + b) \ sum _ {n = 0} ^ {\ infty} \ left ({\ frac {(2n-3) !!} {2 ^ {n} n!}} \ right) ^ {2} h ^ {n} \\ = \ pi (a + b) \ left [ 1 + {\ frac {h} {4}} + \ sum _ {n = 2} ^ {\ infty} \ left ({\ frac {(2n-3) !!} {2 ^ {n} n!} } \ right) ^ {2} h ^ {n} \ right] \\ = \ pi (a + b) \ left [1+ \ sum _ {n = 1} ^ {\ infty} \ left ({\ frac {(2n-1) !!} {2 ^ {n} n!}} \ right) ^ {2} {\ frac {h ^ {n}} {(2n-1) ^ {2}}} \ справа]. \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d29d8f31216e5d32400e99b04e75e242d987893)

![{\ displaystyle C \ приблизительно \ pi {\ biggl [} 3 (a + b) - {\ sqrt {(3a + b) (a + 3b)}} {\ biggr]} = \ pi {\ biggl [} 3 (a + b) - {\ sqrt {10ab + 3 \ left (a ^ {2} + b ^ {2} \ right)}} {\ biggr]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86c8a7234c16af19a7338faafe61b4cf9a333f80)








![{\displaystyle s=-b\left[E\left(z\;{\Biggl |}\;1-{\frac {a^{2}}{b^{2}}}\right)\right]_{\arccos {\frac {x_{1}}{a}}}^{\arccos {\frac {x_{2}}{a}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed75c6daa97d1f19f90b6a53c3441bf0e65601a2)



















 - радиус на апоапсисе (самое дальнее расстояние)
- радиус на апоапсисе (самое дальнее расстояние) - радиус в перицентре (ближайшее расстояние)
- радиус в перицентре (ближайшее расстояние) - длина большой полуоси
- длина большой полуоси 




![{\ displaystyle {\ begin {align} a = {\ frac {r_ {a} + r_ {p}} {2}} \\ [2pt] b = {\ sqrt {r_ {a} r_ {p}} } \\ [2pt] \ ell = {\ frac {2} {{\ frac {1} {r_ {a}}} + {\ frac {1} {r_ {p}}}}} = {\ frac {2r_ {a} r_ {p}} {r_ {a} + r_ {p}}} \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08835a73be73e7094f529d4eff42804930898271) .
.