Ромб

Для использования в других целях, см ромб (значения).

Ромб
Два ромба
Тип	четырехугольник, трапеция, параллелограмм, воздушный змей
Ребра и вершины	4
Символ Шлефли	{} + {} {2 α }
Диаграмма Кокстера
Группа симметрии	Двугранный (D 2), [2], (* 22), порядок 4
Площадь	${\ Displaystyle К = {\ гидроразрыва {п \ cdot q} {2}}}$ (половина произведения диагоналей)
Двойной многоугольник	прямоугольник
Характеристики	выпуклый, изотоксальный

Ромб имеет квадрат как частный случай и является частным случаем воздушного змея и параллелограмма.

В плоскости евклидовой геометрии, A ромб (множественные число ромбов или ромбы) представляет собой четырехугольник, чьи четырех сторон все имеют одинаковую длину. Другое название - равносторонний четырехугольник, поскольку равносторонний означает, что все его стороны равны по длине. Ромб часто называют бриллиантом в честь масти бриллиантов на игральных картах, которая напоминает проекцию восьмигранного ромба или ромб, хотя первый иногда конкретно относится к ромбу с углом 60 ° (который некоторые авторы называют калиссоном после французское сладкое - также см. Полиамонд ), а последнее иногда относится именно к ромбу с углом 45 °.

Каждый ромб простой (не самопересекающийся) и является частным случаем параллелограмма и воздушного змея. Ромб с прямыми углами - это квадрат.

• 1 Этимология
• 2 Характеристики
• 3 Основные свойства
• 4 диагонали
• 5 Inradius
• 6 Площадь
• 7 Двойные свойства
• 8 декартово уравнение
• 9 Другая недвижимость
  • 9.1 Как грани многогранника
• 10 См. Также
• 11 Источники
• 12 Внешние ссылки

Слово «ромб» происходит от древнегреческого : ῥόμβος, латинизировано : rhombos, что означает нечто, что вращается, что происходит от глагола ῥέμβω, латинизированного: rhémbō, что означает «вращаться и кружиться ». Это слово использовали как Евклид, так и Архимед, которые использовали термин «сплошной ромб» для двуконуса, двух правильных круговых конусов, имеющих общее основание.

Поверхность, которую мы сегодня называем ромбом, представляет собой поперечное сечение биконуса на плоскости, проходящей через вершины двух конусов.

Простой (не самопересекающийся ) четырехугольник является ромбом тогда и только тогда, когда он представляет собой любое одно из следующих действий:

• параллелограмм, в котором диагональ делит пополам внутренний угол
• параллелограмм, у которого по крайней мере две последовательные стороны равны по длине
• параллелограмм, в котором диагонали перпендикулярны ( ортодиагональный параллелограмм)
• четырехугольник с четырьмя сторонами одинаковой длины (по определению)
• четырехугольник, в котором диагонали перпендикулярны и делят друг друга пополам
• четырехугольник, в котором каждая диагональ делит пополам два противоположных внутренних угла
• четырехугольник ABCD, обладающая точкой Р в его плоскости таким образом, что четыре треугольника ABP, BCP, CDP, и DAP все конгруэнтен
• четырехугольник ABCD, в котором вписанные окружности в треугольники ABC, BCD, CDA и DAB имеют общую точку

Каждый ромб имеет две диагонали, соединяющие пары противоположных вершин, и две пары параллельных сторон. Используя равные треугольники, можно доказать, что ромб симметричен по каждой из этих диагоналей. Отсюда следует, что любой ромб обладает следующими свойствами:

• Противоположные углы ромба имеют равную меру.
• Две диагонали ромба перпендикулярны ; то есть ромб - это ортодиагональный четырехугольник.
• Его диагонали делят пополам противоположные углы.

Первое свойство означает, что каждый ромб является параллелограммом. Следовательно, ромб обладает всеми свойствами параллелограмма : например, противоположные стороны параллельны; смежные углы являются дополнительными ; две диагонали делят друг друга пополам ; любая линия, проходящая через среднюю точку, делит площадь пополам; а сумма квадратов сторон равна сумме квадратов диагоналей ( закон параллелограмма ). Таким образом, обозначая общую сторону как a, а диагонали как p и q, в каждом ромбе

${\ displaystyle \ displaystyle 4a ^ {2} = p ^ {2} + q ^ {2}.}$

Не каждый параллелограмм является ромбом, хотя любой параллелограмм с перпендикулярными диагоналями (второе свойство) является ромбом. В общем, любой четырехугольник с перпендикулярными диагоналями, одна из которых является линией симметрии, является воздушным змеем. Каждый ромб - это воздушный змей, а любой четырехугольник, который одновременно является воздушным змеем и параллелограммом, - ромбом.

Ромб - это касательный четырехугольник. То есть он имеет вписанную окружность, касательную ко всем четырем сторонам.

Ромб. Каждый угол, отмеченный черной точкой, является прямым. Высота h - это расстояние по перпендикуляру между любыми двумя несмежными сторонами, которое равно диаметру вписанной окружности. Диагонали длин p и q - это отрезки красной пунктирной линии.

Длину диагоналей p = AC и q = BD можно выразить через сторону ромба a и угол при вершине α как

${\ displaystyle p = a {\ sqrt {2 + 2 \ cos {\ alpha}}}}$

а также

${\ displaystyle q = a {\ sqrt {2-2 \ cos {\ alpha}}}.}$

Эти формулы являются прямым следствием закона косинусов.

Внутренний радиус (радиус окружности, вписанной в ромб), обозначаемый r, может быть выражен через диагонали p и q как

${\ displaystyle r = {\ frac {p \ cdot q} {2 {\ sqrt {p ^ {2} + q ^ {2}}}}},}$

или с точки зрения длины стороны a и любого угла при вершине α или β как

${\ displaystyle r = {\ frac {a \ sin \ alpha} {2}} = {\ frac {a \ sin \ beta} {2}}.}$

Что касается всех параллелограммов, площадь K ромба равна произведению его основания и его высоты ( h). Основание - это просто любая сторона длиной a:

${\ Displaystyle К = а \ cdot ч.}$

Площадь также может быть выражена как квадрат основания, умноженный на синус любого угла:

${\ Displaystyle К = а ^ {2} \ CDOT \ грех \ альфа = а ^ {2} \ CDOT \ грех \ бета,}$

или по высоте и углу при вершине :

${\ Displaystyle К = {\ гидроразрыва {ч ^ {2}} {\ грех \ альфа}},}$

или как половину произведения диагоналей p, q:

${\ Displaystyle К = {\ гидроразрыва {p \ cdot q} {2}},}$

или как полупериметром раз радиус из круга, вписанного в ромб (inradius):

${\ displaystyle K = 2a \ cdot r.}$

Другой способ, аналогичный параллелограммам, состоит в том, чтобы рассматривать две соседние стороны как векторы, образующие бивектор, поэтому площадь - это величина бивектора (величина векторного произведения двух векторов), которая является определителем двух Декартовы координаты векторов: K = x 1 y 2 - x 2 y 1.

Двойной многоугольник ромба является прямоугольником :

• У ромба все стороны равны, а у прямоугольника все углы равны.
• У ромба противоположные углы равны, а у прямоугольника равны противоположные стороны.
• Ромб имеет вписанную окружность, в то время как прямоугольник имеет окружность.
• Ромб имеет ось симметрии через каждую пару противоположных углов при вершине, в то время как прямоугольник имеет ось симметрии через каждую пару противоположных сторон.
• Диагонали ромба пересекаются под равными углами, а диагонали прямоугольника равны по длине.
• Фигура, образованная соединением середин сторон ромба, представляет собой прямоугольник, и наоборот.

Стороны ромба с центром в начале координат с диагоналями, каждая из которых падает на ось, состоят из всех точек ( x, y), удовлетворяющих условиям

${\ displaystyle \ left | {\ frac {x} {a}} \ right | \! + \ left | {\ frac {y} {b}} \ right | \! = 1.}$

Вершины находятся в точке и Это частный случай суперэллипса с показателем 1. ${\ displaystyle (\ pm a, 0)}$${\ displaystyle (0, \ pm b).}$

• Одним из пяти типов двумерных решеток является ромбическая решетка, также называемая центрированной прямоугольной решеткой.
• Одинаковые ромбики могут мозаику двухмерной плоскости тремя разными способами, в том числе, для ромба 60 °, мозаика ромбовидной формы.

Как топологические квадратные мозаики		Как ромбовидная плитка под углом 30-60 градусов

• Трехмерные аналоги ромба включают бипирамиду и биконус.
• Некоторые многогранники имеют ромбические грани, такие как ромбический додекаэдр и трапеции-ромбический додекаэдр.

Некоторые многогранники со всеми ромбическими гранями

Изоэдральные многогранники		Неизоэдральные многогранники
Идентичные ромбы	Идентичные золотые ромбы		Два вида ромбов	Три вида ромбов
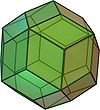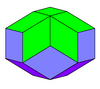Ромбический додекаэдр	Ромбический триаконтаэдр	Ромбический икосаэдр	Ромбический эннеконтаэдр	Ромбоэдр

Как грани многогранника

Ромбоэдр (также называемый ромбические шестигранники) представляет собой трехмерную фигуру как параллелепипеда (также называемый прямоугольный параллелепипед), за исключением того, что ее 3 пары параллельных граней до 3 -х типов ромбов вместо прямоугольников.

Ромбический додекаэдр является выпуклым многогранник с 12 конгруэнтными ромбами как его грани.

Ромбический триаконтаэдр является выпуклым многогранник с 30 золотыми ромбами (ромбы, диагонали которого находится в золотая пропорция ) в качестве его граней.

Большое ромбический триаконтаэдр является невыпуклым равногранным, isotoxal полиэдр с 30 пересекающимися ромбическими гранями.

Ромбический hexecontahedron является плеяде'ученым из ромбического триаконтаэдра. Он невыпуклый, с 60 золотыми ромбическими гранями с икосаэдрической симметрией.

Ромбическое enneacontahedron многогранник, состоящий из 90 ромбических граней, причем три, пять, шесть или ромбов встречи в каждой вершине. В нем 60 широких ромбов и 30 тонких.

Trapezo-ромбический додекаэдр представляет собой выпуклый многогранник с 6 ромбическими и 6 трапециевидным лицом.

Ромбические Икосаэдр многогранник состоит из 20 ромбических граней, из которых три, четыре или пять встречаются в каждой вершине. У него 10 граней на полярной оси и 10 граней, следующих за экватором.

• Меркель-Рауте
• Ромб Михаэлиса в анатомии человека
• Ромбовидный параллелепипед или параллелограмм, который не является ни ромбом, ни прямоугольником.
• Ромбическая антенна
• Ромбические шахматы
• Флаг департамента Северный Сантандер Колумбии, содержащий четыре звезды в форме ромба
• Суперэллипс (включает ромб с закругленными углами)

• Параллелограмм и ромб - Анимированный курс (Построение, Окружность, Площадь)
• Определение ромба, Math Open Reference с интерактивным апплетом.
• Область ромба, Math Open Reference - показывает три различных способа вычисления площади ромба с помощью интерактивного апплета.