В геометрии, A многогранник (например, многоугольник или многогранник ), или плиточный, является isotoxal или края транзитивны, если его симметрия действует транзитивно по его краям. Неформально это означает, что у объекта есть только один тип ребра: при наличии двух ребер происходит перемещение, вращение и / или отражение, которые перемещают один край к другому, оставляя область, занятую объектом, неизменной.
Термин « изотоксал» происходит от греческого τόξον, означающего дугу.
Изотоксальный многоугольник - это четный равносторонний многоугольник, но не все равносторонние многоугольники изотоксальны. В двойственных из isotoxal полигонов изогональных многоугольники. 4 n -угольники центрально-симметричны, так же как и зоногоны.
В общем, изотоксальный 2 n -угольник будет иметь диэдральную симметрию D n (* nn ). Ромб является isotoxal многоугольник с D 2 (* 22) симметрии. Все правильные многоугольники ( равносторонний треугольник, квадрат и т. Д.) Изотоксальны, имеют двойной минимальный порядок симметрии: правильный n -угольник имеет диэдральную симметрию D n (* nn).
Изотоксальный 2 n -угольник можно обозначить как {n α } с самым внешним внутренним углом α. Второй внутренний угол β может быть больше или меньше 180 градусов, образуя выпуклые или вогнутые многоугольники. Звездные многоугольники также могут быть изотоксальными, обозначенными как {( n / q ) α }, с q lt; n -1 и НОД ( n, q ) = 1, где q - число поворота или плотность. Вогнутые внутренние вершины могут быть определены при q lt; n / 2. Если есть наибольший общий делитель, как, {( па / QA) α } может быть уменьшена как соединение с {( п / д) amp; alpha ; }, с скопирована повернуты.
Набор однородных мозаик можно определить с помощью изотоксальных многоугольников как нижний тип правильных граней.
| Стороны (2 шт. ) | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
|---|---|---|---|---|---|---|---|
| {n α } Выпуклая β lt;180 Вогнутая βgt; 180 | |   {3 α } {3 α } |   {4 α } {4 α } |   {5 α } {5 α } |   {6 α } {6 α } |   {7 α } {7 α } |   {8 α } {8 α } |
| 2-поворотный {( n / 2) α } | - |  {(3/2) α } {(3/2) α } |  2 {2 α } 2 {2 α } | 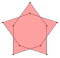  {(5/2) α } {(5/2) α } |   2 {3 α } 2 {3 α } |   {(7/2) α } {(7/2) α } |   2 {4 α } 2 {4 α } |
| 3-поворотный {( n / 3) α } | - | - |  {(4/3) α } {(4/3) α } |  {(5/3) α } {(5/3) α } |  3 {2 α } 3 {2 α } |   {(7/3) α } {(7/3) α } |   {(8/3) α } {(8/3) α } |
| 4 поворота {( n / 4) α } | - | - | - |  {(5/4) α } {(5/4) α } |  2 {(3/2) α } 2 {(3/2) α } |  {(7/4) α } {(7/4) α } |  4 {2 α } 4 {2 α } |
| 5 витков {( n / 5) α } | - | - | - | - |  {(6/5) α } {(6/5) α } |  {(7/5) α } {(7/5) α } |  {(8/5) α } {(8/5) α } |
| 6 витков {( n / 6) α } | - | - | - | - | - |  {(7/6) α } {(7/6) α } |  2 {(4/3) α } 2 {(4/3) α } |
| 7 витков {( n / 7) α } | - | - | - | - | - | - |  {(8/7) α } {(8/7) α } |
Правильные многогранники изоэдральны (транзитивны по граням), изогональны (транзитивны по вершинам) и изотоксальны (транзитивны по ребрам).
Квазирегулярные многогранники, такие как кубооктаэдр и икосододекаэдр, изогональны и изотоксальны, но не изоэдральны. Их двойники, включая ромбический додекаэдр и ромбический триаконтаэдр, изоэдральны и изотоксальны, но не изогональны.
| Квазирегулярный многогранник | Квазирегулярный двойственный многогранник | Квазирегулярный звездный многогранник | Квазирегулярный двойной звездный многогранник | квазирегулярные плиточные | Квазирегулярные двойной плиточные |
|---|---|---|---|---|---|
 Кубооктаэдр является изогональным и isotoxal полиэдра Кубооктаэдр является изогональным и isotoxal полиэдра |  Ромбический додекаэдр является равногранным и isotoxal полиэдра Ромбический додекаэдр является равногранным и isotoxal полиэдра |  Большой икосододекаэдр является Изогональной и isotoxal звезды многогранник Большой икосододекаэдр является Изогональной и isotoxal звезды многогранник |  Большой ромбические триаконтаэдра является равногранной и isotoxal звезды многогранник Большой ромбические триаконтаэдра является равногранной и isotoxal звезды многогранник |  Trihexagonal Черепица является Изогональным и isotoxal плиточной Trihexagonal Черепица является Изогональным и isotoxal плиточной |  Rhombille плиточные является равногранным и isotoxal плиточным с p6m (* 632) симметрии. Rhombille плиточные является равногранным и isotoxal плиточным с p6m (* 632) симметрии. |
Не каждый многогранник или двумерная мозаика, построенная из правильных многоугольников, изотоксальна. Например, усеченный икосаэдр (известный футбольный мяч) не является изотоксальным, поскольку у него есть два типа ребер: шестиугольник-шестиугольник и шестиугольник-пятиугольник, и симметрия твердого тела не может перемещать ребро шестиугольника-шестиугольника на поверхность. край шестиугольника-пятиугольника.
Изотоксальный многогранник имеет одинаковый двугранный угол для всех ребер.
Двойник выпуклого многогранника также является выпуклым многогранником.
Двойник невыпуклого многогранника также является невыпуклым многогранником. (По контрасту.)
Двойник изотоксального многогранника также является изотоксальным многогранником. (См. Статью Двойной многогранник. )
Существует девять выпуклых изотоксальных многогранников: пять ( правильных ) Платоновых тел, два ( квазирегулярных ) общих ядра двойных Платоновых тел и их два двойных.
Существует четырнадцать невыпуклых изотоксальных многогранников: четыре (правильных) многогранника Кеплера – Пуансо, два (квазирегулярных) общих ядра двойственных многогранников Кеплера – Пуансо и их два двойных, а также три квазирегулярных дитригональных (3 | p q ) звезды многогранники и три двойных к ним.
Существует по крайней мере пять изотоксальных полиэдрических соединений: пять правильных полиэдрических соединений ; их пять двойников также являются пятью правильными полиэдрическими соединениями (или одним хиральным двойником).
Существует по крайней мере пять изотоксальных многоугольных мозаик евклидовой плоскости и бесконечно много изотоксальных многоугольных мозаик гиперболической плоскости, включая конструкции Уитхоффа из регулярных гиперболических мозаик { p, q } и неправые ( pqr) группы.