Войти
| Икосододекаэдр | |
|---|---|
 . (Нажмите здесь, чтобы вращать модель) | |
| Тип | Архимедово твердое тело. Однородный многогранник |
| Элементы | F = 32, E = 60, V = 30 (χ = 2) |
| Грани по сторонам | 20 {3} +12 {5} |
| Обозначение Конвея | aD |
| символы Шлефли | r {5,3} |
| t1{5,3} | |
| символ Wythoff | 2 | 3 5 |
| Диаграмма Кокстера |     |
| Группа симметрии | Ih, H 3, [5,3], (* 532), порядок 120 |
| Группа вращения | I, [5, 3], (532), порядок 60 |
| Двугранный угол | 142,62 °.  |
| Ссылки | U 24, C 28, W 12 |
| Свойства | Полурегулярный выпуклый квазирегулярный |
 . Цветные грани |  . 3.5.3.5. (Вершинная фигура ) |
 . Ромбический триаконтаэдр. (двойной многогранник ) |  . Сеть |
3D-модель икосододекаэдра В геометрии икосододекаэдр представляет собой многогранник с двадцатью (икоси) треугольными гранями и двенадцатью (додека) пятиугольниками. Икосододекаэдр имеет 30 идентичных вершин, в каждой из которых встречаются два треугольника и два пятиугольника, и 60 идентичных ребер, каждое из которых отделяет треугольник от пятиугольника. Таким образом, он является одним из архимедовых тел и более конкретно, a квазирегулярный многогранник.
Икосододекаэдр имеет симметрию икосаэдра, и его первая звёздчатая форма представляет собой соединение додекаэдра и его двойного икосаэдра, причем вершины икосододекаэдра расположены в середине каждого из ребер.
Его двойственный многогранник - это ромбический триаконтаэдр. Икосододекаэдр можно разделить вдоль любой из шести плоскостей, чтобы сформировать пару пятиугольных ротондов, которые относятся к телам Джонсона.
. Икосододекаэдр можно рассматривать как пятиугольную гиробиротонду, как комбинацию двух круглых (сравните пятиугольную ортобиротонду, одно из тел Джонсона ). В этой форме его симметрия D5d, [10,2], (2 * 5), порядок 20.
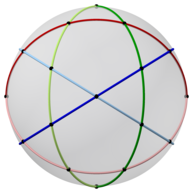
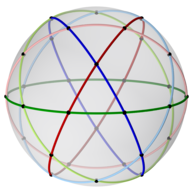
каркасная фигура икосододекаэдра состоит из шести плоские правильные десятиугольники, встречающиеся попарно в каждой из 30 вершин.
Икосододекаэдр имеет 6 центральных декагонов. Спроецированные в сферу, они определяют 6 больших кругов. Бакминстер Фуллер использовал эти 6 больших кругов вместе с 15 и 10 другими в двух других многогранниках, чтобы определить свой 31 большой круг сферического икосаэдра.
Удобно Декартовы координаты для вершин икосододекаэдра с единичными ребрами задаются четными перестановками из:
, где φ - золотое сечение, 1 + √5 / 2.
Икосододекаэдр имеет четыре специальных ортогональных проекции с центрами на вершине, ребре, треугольной грани и пятиугольной грани. Последние два соответствуют плоскостям Кокстера A 2 и H 2.
| Центрированы по | Vertex | Edge | Грань. Треугольник | Грань. Пентагон |
|---|---|---|---|---|
| Сплошной |  |  |  | |
| Каркас |  |  |  |  |
| Проективная. симметрия | [2] | [2 ] | [6] | [10] |
| Двойной |  |  |  |  |
Площадь поверхности A и объем V икосододекаэдра с длиной ребра a составляют:
60 ребер образуют 6 декагонов, соответствующих большим кругам в сферической мозаике. Икосододекаэдр также может быть представлен в виде сферической мозаики и спроецирован на плоскость через стереографическую проекцию . Эта проекция конформна, сохраняя углы, но не площади или длины. Прямые на сфере проецируются как дуги окружности на плоскость.
 |  . Пентагон с центром |  . Треугольник с центром |
| Ортогональная проекция | Стереографические проекции | |
|---|---|---|
| Ортографические проекции | ||||
|---|---|---|---|---|
 |  |  | ||
| 2-х, 3-х и 5-ти кратные оси симметрии | ||||
Икосидодекаэдр - это исправленный додекаэдр, а также выпрямленный икосаэдр, существующий как усечение по всем ребрам между этими правильными твердые тела.
Икосододекаэдр содержит 12 пятиугольников додекаэдра и 20 треугольников икосаэдра :
| семейства однородных икосаэдрических многогранников | |||||||
|---|---|---|---|---|---|---|---|
| Симметрия : [5, 3], (* 532) | [5,3], (532) | ||||||
 |  |  |  |  |  |  |  |
| | | | | | |  |
| {5,3} | t {5,3} | r {5, 3} | t {3,5} | {3,5} | rr {5,3} | tr {5,3} | sr {5,3} |
| Duals в однородные многогранники | |||||||
 |  |  |  |  |  |  |  |
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4. 6.10 | V3.3.3.3.5 |
Икосододекаэдр существует в последовательности симметрий квазирегулярных многогранников и мозаик с конфигурациями вершин (3.n), переходящих от мозаик сферы к евклидовой плоскости. и в гиперболическую плоскость. При орбифолдной нотации симметрии * n32 все эти мозаики являются конструкцией Уайтхоффа в пределах фундаментальной области симметрии, с образующими точками в правом углу области.
| * n32 орбифолдные симметрии квазирегулярных мозаик : (3.n) | |||||||
|---|---|---|---|---|---|---|---|
 . Конструкция | Сферическая | евклидова | гиперболическая | ||||
| * 332 | * 432 | * 532 | * 632 | * 732 | * 832... | * ∞32 | |
| Квазирегулярный. цифры |  |  |  |  |  |  |  |
| Vertex | (3.3) | (3.4) | (3.5) | (3.6) | (3.7) | (3.8) | (3. ∞) |
* 5n2 мутации симметрии квазирегулярных мозаик: (5.n) [
| ||||||||
|---|---|---|---|---|---|---|---|---|
| Симметрия. * 5n2. [n, 5] | Сферическая | Гиперболическая | Паракомпактная | Некомпактный | ||||
| * 352. [3,5] | * 452. [4,5] | * 552. [5, 5] | * 652. [6,5] | * 752. [7,5] | * 852. [8,5]... | * ∞52. [∞, 5] | . [ni, 5] | |
| Цифры |  |  |  |  |  |  |  | |
| Конфигурация | (5.3) | (5.4) | (5.5) | (5.6) | (5.∞) | (5.ni) | ||
| Ромбический. цифры |  |  |  |  | ||||
| Config. | V(5.3) | V(5.4) | V(5.5) | V(5.6) | V (5.7) | V (5.8) | V (5.∞) | V (5.∞) |
Икосододекаэдр связан с телом Джонсона. называется пятиугольной ортобиротондой, образованной двумя пятиугольными ротондами, соединенными как зеркальные изображения. Таким образом, икосододекаэдр можно назвать пятиугольной гиробиротондой с вращением между верхней и нижней половинами.
 . (Рассечение) |
|
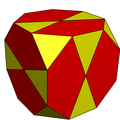Икосододекаэдр в усеченном кубе Усеченный куб 105>можно превратить в икосододекаэдр, разделив восьмиугольники на два пятиугольника и два треугольника. Он имеет пиритоэдрическую симметрию.
Восемь однородных звездных многогранников имеют одинаковое расположение вершин. Из них два также имеют одинаковое расположение ребер : малый икосигемидодекаэдр (имеющий общие треугольные грани) и малый додекагемидодекаэдр (имеющий пятиугольные грани в общем). Расположение вершин также совпадает с соединениями из пяти октаэдров и пяти тетрагемигексаэдров.
 . икосидодекаэдра |  . малого икосигемидодекаэдра |  . малого додекагемидодекаэдра | ||||||||||||||
 . большого икосододекаэдра |  . Большой додекагемидодекаэдр |  . Большой икосигемидодекаэдр | ||||||||||||||
 . Додекадодекаэдр |  . Малый додекагемикосаэдр |  . Большой додекагемикосаэдр | ||||||||||||||
 . Соединение пяти октаэдров |  . Соединение пяти тетрахемигексэдров | . Связанные многогранники <5>в четырехмерной геометрии икосододекаэдр появляется в регулярном 600-ячеечном как экваториальный срез, который принадлежит первому вершине прохода 600-ячеек через 3D Космос. Другими словами: 30 вершин 600-ячейки, которые лежат на расстоянии 90 градусов по дуге ее описанной гиперсферы от пары противоположных вершин, являются вершинами икосододекаэдра. Каркас 600-элементного блока состоит из 72 плоских правильных декагонов. Шесть из них являются экваториальными декагонами к паре противоположных вершин. Это в точности шесть декагонов, которые образуют проволочную рамку икосододекаэдра. Икосододекаэдрический граф
В математическом поле теории графов, икосододекаэдр - это граф вершин и ребер икосододекаэдра, одного из архимедовых тел. Он имеет 30 вершин и 60 ребер и является графом четвертой степени Архимедовым графом. Общая информация В Вселенной Звездного пути, цель вулканской логической игры Кал-То - создать голографический икосододекаэдр. В одной из книг серии «Аксиома» Тима Пратта «Неправильные звезды» у Елены по обе стороны от нее находится машина икосододекаэдра. [Мягкая обложка, стр. 336] Сфера Хобермана является икосадодекаэдром. См. Также Примечания Ссылки
Внешние ссылки
Последняя правка сделана 2021-05-23 10:20:40
Содержание доступно по лицензии CC BY-SA 3.0 (если не указано иное). 
| ||||||||||||||
. Пятиугольная ортобиротонда
. Пятиугольная ротонда
5-кратная симметрия 