Войти
Выпуклый правильный икосаэдр В геометрии, икосаэдр (или ) - это многогранник с 20 гранями. Название происходит от древнегреческого εἴκοσι (eíkosi), что означает «двадцать», и от древнегреческого ἕδρα (hédra), что означает «сиденье». Множественное число может быть «икосаэдрами» () или «икосаэдрами».
Существует бесконечно много не похожих форм икосаэдров, некоторые из которых более симметричны, чем другие. Наиболее известен (выпуклый, не звездчатый ) правильный икосаэдр - одно из Платоновых тел - грани которого 20 равносторонние треугольники.
 . Выпуклый правильный икосаэдр |  . Большой икосаэдр |
Есть два объекта, один выпуклый и один невыпуклый, которые можно назвать правильными икосаэдрами. Каждый имеет 30 ребер и 20 граней равностороннего треугольника, по пять пересекающихся в каждой из его двенадцати вершин. Оба имеют симметрию икосаэдра. Термин «правильный икосаэдр» обычно относится к выпуклой разновидности, в то время как невыпуклая форма называется большим икосаэдром.
Выпуклый правильный икосаэдр обычно называют просто правильным икосаэдром, одним из пяти правильных Платоновых тел, и представлен его Символ Шлефли {3, 5}, содержащий 20 треугольных граней, по 5 граней, пересекающихся вокруг каждой вершины.
Его двойственный многогранник - это правильный додекаэдр {5, 3}, имеющий три правильные пятиугольные грани вокруг каждой вершины.
Большой икосаэдр - один из четырех правильных звезд многогранников Кеплера-Пуансо. Его символ Шлефли равен {3, 5/2}. Подобно выпуклой форме, он также имеет 20 равносторонних треугольных граней, но его вершина представляет собой пентаграмму , а не пятиугольник, ведущий к геометрически пересекающимся граням. Пересечения треугольников не представляют новых ребер.
Его двойственный многогранник - это большой звездчатый додекаэдр {5/2, 3}, имеющий три правильные пятиугольные грани звезды вокруг каждой вершины.
Звездчатые - это процесс удлинения граней или ребер многогранника до тех пор, пока они не встретятся, чтобы сформировать новый многогранник. Делается это симметрично, чтобы получившаяся фигура сохранила общую симметрию родительской фигуры.
В своей книге Пятьдесят девять икосаэдров, Coxeter et al. перечислил 58 таких звёздчатых звёзд правильного икосаэдра.
Многие из них имеют одну грань в каждой из 20 плоскостей граней и также являются икосаэдрами. Среди них - большой икосаэдр.
Другие звёздчатые формы имеют более одной грани в каждой плоскости или образуют соединения более простых многогранников. Это не совсем икосаэдры, хотя их часто называют таковыми.
| пиритоэдрической и тетраэдрической симметриями | |||||
|---|---|---|---|---|---|
| диаграммами Кокстера |     (пиритоэдрический)  . (четырехгранный)  | ||||
| символ Шлефли | s {3,4}. sr {3,3} или  | ||||
| Грани | 20 треугольников:. 8 равносторонних. 12 равнобедренных | ||||
| Ребер | 30 (6 коротких + 24 длинных) | ||||
| Вершины | 12 | ||||
| Группа симметрии | Th, [4,3], (3 * 2), порядок 24 | ||||
| Группа вращения | Td, [3,3], (332), порядок 12 | ||||
| Двойной многогранник | Пиритоэдр | ||||
| Свойства | выпуклый | ||||
 . Сеть | |||||
| |||||
Правильный икосаэдр может быть искажен или размечен как более низкая пиритоэдрическая симметрия и называется курносым октаэдром, курносым тетраэдром, курносым тетраэдр и псевдоикосаэдр . Это можно рассматривать как чередованный усеченный октаэдр. Если все треугольники равносторонние, симметрию также можно отличить, раскрасив по-разному наборы треугольников 8 и 12.
Пиритоэдрическая симметрия имеет символ (3 * 2), [3,4], с порядком 24. Тетраэдрическая симметрия имеет символ (332), [3,3], с порядком 12. Эти более низкие симметрии допускают геометрические искажения от 20 равносторонних треугольных граней, вместо 8 равносторонних треугольников и 12 конгруэнтных равнобедренных треугольников.
Эти симметрии предлагают диаграммы Кокстера : и соответственно, каждая из которых представляет собой нижняя симметрия до правильного икосаэдра 
, (* 532), [5,3] икосаэдрической симметрии порядка 120.
Построение по вершинам усеченного октаэдра, показывающего внутренние прямоугольники. Координаты 12 вершин могут быть определены векторами, определенными всеми возможными циклическими перестановками и перестановками знаков координат формы (2, 1, 0). Эти координаты представляют собой усеченный октаэдр с удаленными чередующимися вершинами.
Эта конструкция называется курносым тетраэдром в его правильной форме икосаэдра, генерируемой теми же операциями, которые выполняются, начиная с вектора (ϕ, 1, 0), где ϕ - золотое сечение.
Икосаэдр Йессена В икосаэдре Йессена, который иногда называют ортогональным икосаэдром Йессена, 12 равнобедренных граней расположены по-другому, так что фигура не является выпуклой и имеет правые двугранные углы.
Это ножницы, конгруэнтные кубу, что означает, что его можно разрезать на более мелкие многогранные части, которые можно переставить, чтобы сформировать твердый куб.
Ромбический икосаэдр Ромбический икосаэдр - это зоноэдр, состоящий из 20 конгруэнтных ромбов. Его можно получить из ромбического триаконтаэдра , удалив 10 срединных граней. Несмотря на то, что все грани конгруэнтны, ромбический икосаэдр не транзитивен по граням.
Общие икосаэдры с симметриями пирамиды и призмы включают:
Некоторые тела Джонсона являются икосаэдрами:
| J22 | J35 | J36 | J59 | J60 | J92 |
|---|---|---|---|---|---|
 . Гиро-треугольный купол |  . Вытянутый треугольный ортобикупола |  . Вытянутый треугольный гиробикупола |  . Парабиаугментированный додекаэдр |  . Метабиауглеродный додекаэдр |  . Треугольный гебесфеноротунда |
 |  |  |  |  |  |
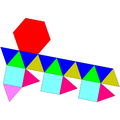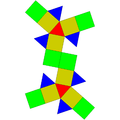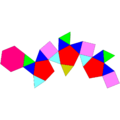| 16 треугольников. 3 квадрата.. 1 шестиугольник | 8 треугольников. 12 квадратов | 8 треугольники. 12 квадратов | 10 треугольников.. 10 пятиугольников | 10 треугольников.. 10 пятиугольников | 13 треугольников. 3 квадрата. 3 пятиугольника. 1 шестиугольник |
.
