| Правильный икосаэдр | |
|---|---|
 . (Нажмите здесь, чтобы посмотреть модель вращения) . (Нажмите здесь, чтобы посмотреть модель вращения) | |
| Тип | Платоново твердое тело |
| Элементы | F = 20, E = 30. V = 12 (χ = 2) |
| Грани по сторонам | 20 {3} |
| Обозначение Конвея | I. sT |
| символы Шлефли | {3,5} |
s {3,4}. sr {3,3} или  | |
| Конфигурация лица | V5.5.5 |
| Символ Wythoff | 5 | 2 3 |
| Диаграмма Кокстера | |
| Симметрия | Ih, H 3, [5,3], (* 532) |
| Группа вращения | I, [5,3], ( 532) |
| Ссылки | U 22, C 25, W 4 |
| Свойства | правильный, выпуклый дельтаэдр |
| Двугранный угол | 138,189685 ° = arccos (- ⁄ 3) |
 . 3.3. 3.3.3. (Вершинная фигура ) . 3.3. 3.3.3. (Вершинная фигура ) |  . Правильный додекаэдр. (двойной многогранник ) . Правильный додекаэдр. (двойной многогранник ) |
 . Сеть . Сеть | |
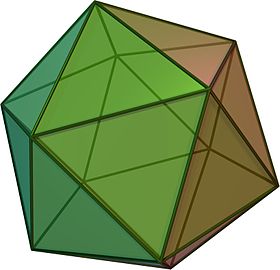
 Трехмерная модель правильного икосаэдра
Трехмерная модель правильного икосаэдра В геометрии, a правильный икосаэдр (или ) представляет собой выпуклый многогранник с 20 гранями, 30 гранями и 12 вершин. Это одно из пяти Платоновых тел, и то, у которого больше всего граней.
У него пять равносторонних треугольных граней, пересекающихся в каждой вершине. Оно представлено символом символ Шлефли {3,5}, или иногда его фигура вершины как 3.3.3.3.3 или 3. Это дуальный додекаэдра , который представлен как {5,3} с тремя пятиугольными гранями вокруг каждой вершины напр.
Правильный икосаэдр - это строго выпуклый дельтаэдр и гиро-удлиненная пятиугольная бипирамида и двуугловая пятиугольная антипризма в любом шести ориентаций.
Название происходит от греческого εἴκοσι (eíkosi) «двадцать» и ἕδρα (hédra) «сиденье». Множественное число может быть «икосаэдрами» или «икосаэдрами» ().
 Сгибание сетки в икосаэдр
Сгибание сетки в икосаэдр Если длина ребра правильного икосаэдра равна a, то радиус описанной сферы (той, которая касается икосаэдра во всех вершинах) составляет
и радиус вписанной сферы (касательная к каждой из граней икосаэдра) равен
, а средний радиус, который касается в середине каждого края это
где ϕ - золотое сечение.
Площадь поверхности A и объем V правильного икосаэдра с длиной ребра a равны:
Последний F = 20-кратный объем обычного тетраэдра с вершиной в центре вписанной сферы, где объем тетраэдра в три раза больше площади основания √3a / 4 его высоты r i.
Коэффициент заполнения объема описанной сферы равен:
 , по сравнению с 66,49% для додекаэдра.
, по сравнению с 66,49% для додекаэдра.Сфера, вписанная в икосаэдр, будет охватывать 89,635% его объема по сравнению до 75,47% для додекаэдра.
Средняя сфера икосаэдра будет иметь объем в 1,01664 раза больше, чем объем икосаэдра, что на сегодняшний день является наиболее близким по объему любому платоническому телу с его средней сферой. Возможно, это делает икосаэдр самым «круглым» из платоновых тел.
 Вершины икосаэдра образуют три ортогональных золотых прямоугольника
Вершины икосаэдра образуют три ортогональных золотых прямоугольника Вершины икосаэдра с центром в начале координат с длиной ребра 2 и радиусом окружности равным 
где ϕ = 1 + √5 / 2 - золотое сечение.
В результате всех перестановок (а не только циклических) получается соединение двух икосаэдров.
Обратите внимание, что эти вершины образуют пять наборов из трех концентрических, взаимно ортогональных золотых прямоугольников, ребра которых образуют кольца Борромео.
Если исходный икосаэдр имеет длину ребра 1, его двойственный додекаэдр имеет длину ребра √5 - 1/2 = 1 / ϕ = ϕ - 1.
 Модель икосаэдра из металлических сфер и магнитных соединителей
Модель икосаэдра из металлических сфер и магнитных соединителей 12 ребер правильного октаэдра можно разделить в золотом сечении так, чтобы результирующие вершины определяли иглярный икосаэдр. Это делается путем размещения векторов по краям октаэдра таким образом, чтобы каждая грань была ограничена циклом, а затем аналогичным образом разделяя каждое ребро на золотую середину в направлении его вектора. пять октаэдров, определяющие любой данный икосаэдр, образуют правильное полиэдрическое соединение, в то время как два икосаэдра, которые могут быть определены таким образом из любого данного октаэдра, образуют соединение однородного многогранника.
 Правильный икосаэдр и его описанная сфера. Вершины правильного икосаэдра лежат в четырех параллельных плоскостях, образуя в них четыре равносторонних треугольника ; это было доказано Папп Александрийский
Правильный икосаэдр и его описанная сфера. Вершины правильного икосаэдра лежат в четырех параллельных плоскостях, образуя в них четыре равносторонних треугольника ; это было доказано Папп Александрийский Расположение вершин правильного икосаэдра можно описать с помощью сферических координат, например, как широта и долгота. Если две вершины взяты на северном и южном полюсах (широта ± 90 °), то остальные десять вершин находятся на широте ± arctan (1/2) ≈ ± 26,57 °. Эти десять вершин находятся на равном расстоянии друг от друга по долготе (36 ° друг от друга), чередуя северную и южную широты.
Эта схема использует тот факт, что правильный икосаэдр представляет собой пятиугольную гировидную бипирамиду с диэдральной симметрией D 5d, т. Е. Образован двумя конгруэнтными пятиугольными пирамиды, соединенные пятиугольной антипризмой.
Икосаэдр имеет три специальных ортогональных проекции с центрами на грани, ребре и вершине:
| Центрировано по | Грань | Ребро | Вершина |
|---|---|---|---|
| Плоскость Кокстера | A2 | A3 | H3 |
| График |  |  |  |
| Проективная. симметрия | [ 6] | [2] | [10] |
| График |  . Нормаль к грани . Нормаль к грани |  . Нормаль к краю . Нормаль к краю |  . Нормаль к вершине . Нормаль к вершине |
Икосаэдр также может быть представлен в виде сферической мозаики и спроецирован на плоскость через стереографическую проекцию . Эта проекция конформна, сохраняя углы, но не площади или длины. Прямые на сфере проецируются как дуги окружности на плоскость.
 | 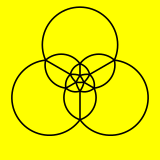 |
| Ортографическая проекция | Стереографическая проекция |
|---|
 . Икосаэдр. H3плоскость Кокстера . Икосаэдр. H3плоскость Кокстера |  . 6-ортоплекс. D6Плоскость Кокстера . 6-ортоплекс. D6Плоскость Кокстера |
| Эту конструкцию геометрически можно рассматривать как 12 вершин 6-ортоплекса, спроецированных в 3 измерения. Это представляет собой геометрическое складывание групп Кокстера от D 6 до H 3 : . Видно этими двумерными ортогональными проекциями плоскости Кокстера, двумя перекрывающимися центральными вершины определяют третью ось в этом отображении. | |
Следующая конструкция икосаэдра позволяет избежать утомительных вычислений в числовом поле ℚ [√5], необходимых в более элементарных подходах.
Существование икосаэдра сводится к существованию шести равноугольных линий в ℝ. Действительно, пересечение такой системы равноугольных прямых с евклидовой сферой с центром в их общем пересечении дает двенадцать вершин правильного икосаэдра, что легко проверить. И наоборот, если предположить существование правильного икосаэдра, прямые, определяемые его шестью парами противоположных вершин, образуют равноугольную систему.
Чтобы построить такую равноугольную систему, мы начнем с этой квадратной матрицы 6 × 6 :

Прямое вычисление дает A = 5I (где I - единичная матрица 6 × 6). Это означает, что A имеет собственных значений –√5 и √5, оба с кратностью 3, поскольку A симметрична и имеет след ноль.
Матрица A + √5I индуцирует, таким образом, евклидову структуру на частном пространстве ℝ / ker (A + √5I), которое изоморфно до ℝ, поскольку ядро ker (A + √5I) для A + √5I имеет размерность 3. Изображение под проекцией π: ℝ → ℝ / ker (A + √5I) шести координатных осей ℝv 1,…, ℝv 6 в ℝ образует, таким образом, систему из шести равносторонних прямых в ℝ, попарно пересекающихся под общим острым углом arccos ⁄ √5. Ортогональная проекция ± v 1,…, ± v 6 на √5-собственное подпространство матрицы A дает, таким образом, двенадцать вершин икосаэдра.
Вторая прямая конструкция икосаэдра использует теорию представлений переменной группы A5, действующей посредством прямых изометрий на икосаэдр.
 Полная Икосаэдрическая симметрия имеет 15 зеркальных плоскостей (на этой сфере обозначены голубыми большими кругами ), пересекающихся в порядке π / 5, π / 3, π / 2 углов, разделяющих сферу на 120 треугольников фундаментальных областей. Есть 6 5-кратных осей (синие), 10 3-кратных осей (красные) и 15 2-кратных осей (пурпурный). Вершины правильного икосаэдра существуют в точках 5-кратной оси вращения.
Полная Икосаэдрическая симметрия имеет 15 зеркальных плоскостей (на этой сфере обозначены голубыми большими кругами ), пересекающихся в порядке π / 5, π / 3, π / 2 углов, разделяющих сферу на 120 треугольников фундаментальных областей. Есть 6 5-кратных осей (синие), 10 3-кратных осей (красные) и 15 2-кратных осей (пурпурный). Вершины правильного икосаэдра существуют в точках 5-кратной оси вращения. Вращательная группа симметрии правильного икосаэдра изоморфна чередующейся группе на пять букв. Эта не- абелева простая группа является единственной нетривиальной нормальной подгруппой из симметричной группы из пяти букв. Поскольку группа Галуа общего уравнения квинтики изоморфна симметрической группе из пяти букв, а эта нормальная подгруппа проста и неабелева, общее уравнение пятой степени не имеет раствор в радикалах. Доказательство теоремы Абеля – Руффини использует этот простой факт, а Феликс Кляйн написал книгу, в которой использовала теорию симметрий икосаэдра для получения аналитического решения общего уравнения пятой степени., (Klein 1884). См. симметрия икосаэдра: связанные геометрии для дальнейшей истории и связанные симметрии семи и одиннадцати букв.
Полная группа симметрии икосаэдра (включая отражения) известна как полная группа икосаэдра и изоморфна произведению группы вращательной симметрии и группы C 2 размера два, которая создается путем отражения через центр икосаэдра.
Икосаэдр имеет большое количество звездчатых элементов. Согласно определенным правилам, изложенным в книге Пятьдесят девять икосаэдров, для правильного икосаэдра было идентифицировано 59 звёздчатых звёзд. Первая форма - это сам икосаэдр. Один из них - правильный многогранник Кеплера – Пуансо. Три являются правильными составными многогранниками.
 . Грани икосаэдра вытянуты наружу при пересечении плоскостей, определяя области в пространстве, как показано на этой диаграмме звёздчатой формы пересечений в одиночный самолет. . Грани икосаэдра вытянуты наружу при пересечении плоскостей, определяя области в пространстве, как показано на этой диаграмме звёздчатой формы пересечений в одиночный самолет. |  |  |  |  |  |  | |
 |  |  |  | ||||
 |  |  |  |  |
малый звездчатый додекаэдр, большой додекаэдр и большой икосаэдр - это три грани правильный икосаэдр. У них одинаковое расположение вершин . У всех 30 ребер. Правильный икосаэдр и большой додекаэдр имеют одинаковое расположение ребер , но различаются гранями (треугольники против пятиугольников), как и маленький звездчатый додекаэдр и большой икосаэдр (пентаграммы против треугольников).
| Выпуклые | Правильные звезды | ||
|---|---|---|---|
| икосаэдр | большой додекаэдр | малый звездчатый додекаэдр | большой икосаэдр |
 |  |  |  |
Икосаэдр искажается., хотя и не являются регулярными, тем не менее однородны по вершинам. Это инвариант относительно тех же вращений, что и тетраэдр, и в некоторой степени аналогичны курносому кубу и курносому додекаэдру, включая некоторые формы которые являются хиральными и некоторые с T h -симметрией, то есть имеют плоскости симметрии, отличные от тетраэдра.
Икосаэдр уникален среди Платоновых тел тем, что имеет двугранный угол не менее 120 °. Его двугранный угол составляет примерно 138,19 °. Таким образом, точно так же, как шестиугольники имеют углы не менее 120 ° и не могут использоваться в качестве граней выпуклого правильного многогранника, поскольку такая конструкция не удовлетворяет требованию, чтобы по крайней мере три грани пересекались в вершине и оставляли положительный дефект для складывания в трех измерениях, икосаэдры не могут использоваться в качестве ячеек выпуклого правильного полихорона, потому что, аналогично, как минимум три ячейки должны встречаться на краю и оставлять положительный дефект для складывания в четырех измерениях (как правило, для выпуклого многогранника в n измерениях по крайней мере три фасетки должны встречаться на пике и оставлять положительный дефект для складывание в n-пространстве). Однако в сочетании с подходящими ячейками, имеющими меньшие двугранные углы, икосаэдры могут использоваться в качестве ячеек в полурегулярных полихорах (например, курносый 24-элементный ), точно так же, как шестиугольники могут использоваться в качестве граней в полурегулярных полихорах (например, курносый 24-элементный ). правильные многогранники (например, усеченный икосаэдр ). Наконец, к невыпуклым многогранникам не предъявляются такие же строгие требования, как к выпуклым многогранникам, и икосаэдры действительно являются ячейками икосаэдра с 120 ячейками, одной из десяти невыпуклых правильных полихор.
Икосаэдр можно также назвать гиродлинной пятиугольной бипирамидой. Ее можно разложить на гироподобную пятиугольную пирамиду и пятиугольную пирамиду или на пятиугольную антипризму и две равные пятиугольные пирамиды.
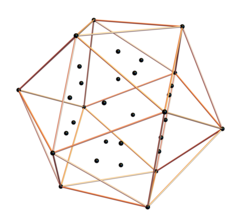
Его можно спроецировать в 3D из 6D 6-полукуба с использованием тех же базисных векторов, которые образуют корпус Ромбический триаконтаэдр из 6-куба. Здесь показаны 20 внутренних вершин, которые не соединены 30 внешними ребрами корпуса с 6D нормальной длиной √2. Внутренние вершины образуют додекаэдр.
. Используемые базисные векторы трехмерной проекции [u, v, w]:
 Икосаэдрическая симметрия подгруппы
Икосаэдрическая симметрия подгруппы Имеется 3 однородных раскраски икосаэдра. Эти раскраски могут быть представлены как 11213, 11212, 11111, назвав 5 треугольных граней вокруг каждой вершины их цветом.
Икосаэдр можно рассматривать как плоскостный тетраэдр, поскольку ослабление правильного тетраэдра дает правильный икосаэдр, имеющий хиральную тетраэдрическую симметрию. Он также может быть построен как чередующийся усеченный октаэдр, имеющий пиритоэдрическую симметрию. Вариант пиритоэдрической симметрии иногда называют псевдоикосаэдром, и он двойственен пиритоэдру.
| Обычный | Однородный | 2-однородный | |||||
|---|---|---|---|---|---|---|---|
| Имя | Правильный. икосаэдр | Курносый. октаэдр | Курносый. тетратетраэдр | Плоский квадрат. бипирамида | Пятиугольник. Гиро-удлиненный. бипирамида | Треугольная. gyrobianticupola | Курносая треугольная. антипризма |
| Изображение |  |  |  |  |  |  |  |
| Лицо. раскраска | (11111) | (11212) | (11213) | (11212) | (11122). (22222) | (12332). (23333) | (11213). (11212) |
| диаграмма Кокстера. | |||||||
| символ Шлефли. | {3,5} | s {3,4} | sr {3,3} | sdt {2,4} | () || {n} || г {п} || () | ss {2,6} | |
| Конвей | I | HtO | sT | HtdP4 | k5A5 | sY3 = HtA3 | |
| Симметрия | Ih. [5,3]. (* 532) | Th. [3,4]. (3 * 2) | T. [3,3]. (332) | D2h. [2, 2]. (* 222) | D5d. [2,10]. (2 * 5) | D3d. [2,6]. (2 * 3) | D3. [3,2]. (322) |
| Симметрия. порядок | 60 | 24 | 12 | 8 | 20 | 12 | 6 |
 Наночастица золота, просматриваемая с помощью просвечивающей электронной микроскопии.
Наночастица золота, просматриваемая с помощью просвечивающей электронной микроскопии. Структура γ-бора.
Структура γ-бора. Многие вирусы, например вирус герпеса, имеет икосаэдрическую оболочку. Вирусные структуры состоят из повторяющихся идентичных субъединиц белка, известных как капсомеры, и икосаэдр является самой простой формой для сборки с использованием этих субъединиц. Используется правильный многогранник, потому что он может быть построен из единственной базовой единицы белка, используемой снова и снова; это экономит место в вирусном геноме.
Также были обнаружены различные бактериальные органеллы икосаэдрической формы. Икосаэдрическая оболочка, инкапсулирующая ферменты и лабильные промежуточные соединения, построена из различных типов белков с доменами BMC.
. В 1904 году Эрнст Геккель описал ряд видов Radiolaria, включая Circogonia icosahedra, скелет которого имеет форму правильного икосаэдра. Копия иллюстрации Геккеля для этого радиолярия появляется в статье о правильных многогранниках.
closo - карбораны - это химические соединения с очень большой формой. близко к икосаэдру. Икосаэдрическое двойникование также встречается в кристаллах, особенно в наночастицах.
Многие бориды и аллотропы бора содержат бор B 12 икосаэдр как элемент базовой конструкции.
 Двадцатигранный кубик из Птолемеевский Египет
Двадцатигранный кубик из Птолемеевский Египет  Двадцатигранный кубик
Двадцатигранный кубик Икосаэдрический кубик с двадцатью сторонами использовался с тех пор древние времена.
В некоторых ролевых играх, таких как Dungeons Dragons, обычно используется двадцатигранный кубик (d20 для краткости) используется для определения успеха или неудачи действия. Эта игральная кость имеет форму правильного икосаэдра. Он может быть дважды пронумерован от «0» до «9» (в этой форме он обычно используется как десятигранный кубик, или d10 ), но большинство современных версий имеют маркировку от «1» до «20». ".
Икосаэдр - трехмерное игровое поле для Icosagame, ранее известного как Ico Crystal Game.
Икосаэдр используется в настольной игре Scattergories для выбора буквы алфавита. Шесть букв опущены (Q, U, V, X, Y и Z).
В игре для Nintendo 64 Kirby 64: The Crystal Shards босс Miracle Matter - это обычный икосаэдр.
Внутри Magic 8-Ball на обычном икосаэдре начертаны различные ответы на да – нет вопросы.
Р. Бакминстер Фуллер и японский картограф Сёдзи Садао разработали карту мира в виде развернутого икосаэдра, названного проекцией Фуллера, максимум которой искажение всего 2%. Американский дуэт электронной музыки ODESZA использует в качестве логотипа обычный икосаэдр.
| Правильный граф икосаэдра | |
|---|---|
 3-кратная симметрия 3-кратная симметрия | |
| Вершины | 12 |
| Ребра | 30 |
| Радиус | 3 |
| Диаметр | 3 |
| Обхват | 3 |
| Автоморфизмы | 120 ( A5 × Z2) |
| Хроматическое число | 4 |
| Свойства | Гамильтониан, регулярный, симметричный, дистанционно-регулярный, дистанционно-транзитивный, 3-связный, планарный граф |
| Таблица графов и параметров | |
скелет икосаэдра (вершины и ребра) образует граф. Это один из 5 платоновых графов, каждый из которых является скелетом своего платонового тела.
Высокая степень симметрии многоугольника повторяется в свойствах этого граф, который является дистанционно-транзитивным и симметричным. Группа автоморфизмов имеет порядок 120. Вершины могут быть окрашены в 4 цвета, ребра окрашены в 5 цветов, а диаметр равен 3.
Граф икосаэдра гамильтониан : есть цикл, содержащий все вершины. Это также планарный граф.
 |
Есть 4 связанных тела Джонсона, включая пятиугольные грани с подмножеством из 12 вершин. Подобный рассеченный правильный икосаэдр имеет 2 уменьшенные смежные вершины, оставляя две трапециевидные грани, а бифастигий имеет 2 удаленных противоположных набора вершин и 4 трапециевидные грани. Пятиугольная антипризма образована удалением двух противоположных вершин.
| Форма | J2 | Bifastigium | J63 | J62 | Рассеченный. икосаэдр | s {2,10} | J11 |
|---|---|---|---|---|---|---|---|
| Вершины | 6 из 12 | 8 из 12 | 9 из 12 | 10 из 12 | 11 из 12 | ||
| Симметрия | C5v, [5], (* 55). порядок 10 | D2h, [2,2], * 222. порядок 8 | C3v, [3], (* 33). порядок 6 | C2v, [2], ( * 22). порядок 4 | D5d, [2,10], (2 * 5). порядок 20 | C5v, [5], (* 55). порядок 10 | |
| Изображение |  |  |  |  |  |  | |
Икосаэдр может быть преобразован с помощью усечения последовательности в его дуальный, додекаэдр:
| Семейство однородных икосаэдрических многогранников | |||||||
|---|---|---|---|---|---|---|---|
| Симметрия : [5,3], (* 532) | [5,3], (532) | ||||||
 |  |  |  |  |  |  |  |
| {5,3} | t { 5,3} | r {5,3} | t {3,5} | {3,5} | rr {5,3} | tr {5,3} | sr {5,3} |
| Двойники однородных многогранников | |||||||
 |  |  |  |  | |||
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
Как курносый тетраэдр, так и чередование усеченного октаэдр также существует в семействах тетраэдрической и октаэдрической симметрии:
| Семейство однородных тетраэдрических многогранников | |||||||
|---|---|---|---|---|---|---|---|
| Симметрия : [3,3], (* 332) | [3,3], (332) | ||||||
 |  |  |  | ||||
| {3,3} | t {3,3} | r {3,3} | t {3,3} | {3, 3} | rr {3,3} | tr {3,3} | sr {3,3} |
| Двойник к однородным многогранникам | |||||||
 |  |  |  | ||||
| V3.3.3 | V3.6.6 | V3.3.3.3 | V3.6.6 | V3.3.3 | V3.4.3.4 | V4.6.6 | V3.3.3.3.3 |
| Однородные октаэдрические многогранники | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия : [4,3], (* 432) | [4,3]. (432) | [1,4,3] = [3,3]. (*332) | [3,4 provided. (3 * 2) | |||||||
| {4,3} | t {4,3} | r {4,3}. r {3} | t{3,4}. t {3} | {3,4}. {3 } | rr {4,3}. s2{3,4} | tr {4,3} | sr {4,3} | h {4,3}. {3,3} | h2{4,3}. t {3,3} | s{3,4}. s {3} |
| Двойные к однородным многогранникам | ||||||||||
| V4 | V3.8 | V (3.4) | V4.6 | V3 | V3.4 | V4.6.8 | V3.4 | V3 | V3.6 | V3 |
Этот многогранник топологически связан как часть последовательности правильных многогранников с символами Шлефли {3, n}, продолжающаяся в гиперболической плоскости.
* n32 мутация симметрии правильных мозаик: {3, n} [
| |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Сферический | Евклид. | Компактный гипер. | Парако. | Некомпактный гиперболический | |||||||
 |  |  |  |  |  |  |  |  |  |  |  |
| 3.3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
Правильный икосаэдр, рассматриваемый как плоскостный тетраэдр, является членом последовательности пренебреженных многогранников и мозаик с вершинной фигурой (3.3.3.3. n) и диаграмма Кокстера – Дынкина ![]()
![]()
![]()
![]()
![]() . Эти фигуры и их двойники имеют (n32) вращательную симметрию, находясь в евклидовой плоскости для n = 6 и гиперболической плоскости для любых более высоких n. Можно считать, что серия начинается с n = 2, с одним набором граней, выродившихся в дигоны.
. Эти фигуры и их двойники имеют (n32) вращательную симметрию, находясь в евклидовой плоскости для n = 6 и гиперболической плоскости для любых более высоких n. Можно считать, что серия начинается с n = 2, с одним набором граней, выродившихся в дигоны.
n32 мутации симметрии курносых мозаик: 3.3.3.3.n
| ||||||||
|---|---|---|---|---|---|---|---|---|
| Симметрия. n32 | Сферический | Евклидово | Компактный гиперболический | Паракомп. | ||||
| 232 | 332 | 432 | 532 | 632 | 732 | 832 | ∞32 | |
| Snub. цифры |  |  |  |  |  |  |  |  |
| Конфиг. | 3.3.3.3.2 | 3.3.3.3.3 | 3.3.3.3.4 | 3.3.3.3.5 | 3.3.3.3.6 | 3.3.3.3.7 | 3.3.3.3.8 | 3.3.3.3.∞ |
| Гироскоп. цифры |  |  |  |  |  |  |  |  |
| Конфиг. | V3.3.3.3.2 | V3.3.3.3.3 | V3.3.3.3.4 | V3.3.3.3.5 | V3.3.3.3.6 | V3.3.3.3.7 | V3. 3.3.3.8 | V3.3.3.3.∞ |
| Сферические | Гиперболические мозаики [
| |||||||
|---|---|---|---|---|---|---|---|---|
 . {2,5}. . {2,5}. |  . {3,5}. . {3,5}. |  . {4, 5}. . {4, 5}. |  . {5,5}. . {5,5}. |  . {6,5}. . {6,5}. |  .. .. |  .. .. | ... |  . {∞, 5}. . {∞, 5}. |
Икосаэдр может замощить гиперболическое пространство в икосаэдре порядка 3 соты, с 3 икосаэдрами вокруг каждого ребра, 12 икосаэдрами вокруг каждой вершины, с символом Шлефли {3,5,3}. Это одна из четырех регулярных мозаик в гиперболическом трехмерном пространстве.
 . Здесь он показан как краевой каркас в модели диска Пуанкаре, с одним видимым икосаэдром в центре. . Здесь он показан как краевой каркас в модели диска Пуанкаре, с одним видимым икосаэдром в центре. |
| Викискладе есть медиафайлы, связанные с Икосаэдром. |
| Wikisource есть текст из Британской энциклопедии 1911 года, статьи Икосаэдр. |
| Найдите икосаэдр в Викисловаре, бесплатном словаре. |
| ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | ||||||||
| Треугольник | Квадрат | p-угольник | Шестиугольник | Пентагон | ||||||||
| Тетраэдр | Октаэдр • Куб | Демикуб | Додекаэдр • Икосаэдр | |||||||||
| 5-элементный | 16-элементный • Тессеракт | Демитессеракт | 24-элементный | 120 ячеек • 600 ячеек | ||||||||
| 5-симплекс | 5-ортоплекс • 5-куб | 5-полукуб | ||||||||||
| 6-симплекс | 6-ортоплекс • 6-куб | 6-полукуб | 122 • 221 | |||||||||
| 7-симплекс | 7-ортоплекс • 7-куб | 7-полукуб | 132 • 231 • 321 | |||||||||
| 8-симплекс | 8-ортоплекс • 8-куб | 8-полукуб | 142 • 241 • 421 | |||||||||
| 9-симплекс | 9-ортоплекс • 9-куб | 9-полукуб | ||||||||||
| 10-симплекс | 10- ортоплекс • 10-куб | 10-полукуб | ||||||||||
| n-симплекс | n-ортоплекс • n- куб | n-полукуб | 1k2 • 2k1 • k21 | n-пятиугольный многогранник | ||||||||
| Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений | ||||||||||||
| Известные звёздчатые формы икосаэдра | |||||||||
| Правильный | Однородные двойники | Регулярные соединения | Правильная звезда | Другие | |||||
| (Выпуклый) икосаэдр | Малый триамбический икосаэдр | Средний триамбический икосаэдр | Большой триамбический икосаэдр | Соединение пяти октаэдров | Соединение пяти тетраэдров | Соединение десяти тетраэдров | Большой икосаэдр | Додекаэдр с выемкой | Конечная звездчатая форма |
|---|---|---|---|---|---|---|---|---|---|
 |  |  |  |  |  |  |  |  | |
 |  |  |  |  |  |  |  |  | |
| Процесс образования звездочки на икосаэдре создает ряд связанных многогранников и соединений с икосаэдрической симметрией. | |||||||||