| Ih, порядок 120 | |||
|---|---|---|---|
| Обычный- | Маленький звездчатый - | Великий- | Великий звездчатый- |
 |  |  |  |
| Th, порядок 24 | T, порядок 12 | Oh, порядок 48 | Джонсон (J 84) |
| Пиритоэдр | Тетартоид | Ромбический- | Треугольный- |
 |  |  |  |
| D4h, порядок 16 | D3h, порядок 12 | ||
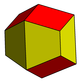
| Ромбо-гексагональный- | Ромбо-квадрат- | Трапецо-ромбический- | Ромбо-треугольный - |
 |  |  |  |
В геометрии додекаэдр (греч. Δωδεκάεδρον, от δώδεκα dōdeka «двенадцать» + ἕδρα hédra «основание», «сиденье» или «грань») означает любое многогранник с двенадцатью плоскими гранями. Самый известный додекаэдр - правильный додекаэдр, который является платоновым телом. Есть также три правильных звездных додекаэдра, которые построены как звездчатые выпуклой формы. Все они имеют икосаэдрическую симметрию, порядок 120.
пиритоэдр, общий крист al форма в пирите, представляет собой неправильный пятиугольный додекаэдр, имеющий ту же топологию (с точки зрения его вершин, как граф), что и обычный, но пиритоэдрической симметрией в то время как тетартоид имеет тетраэдрическую симметрию. ромбический додекаэдр, рассматриваемый как предельный случай пиритоэдра, имеет октаэдрическую симметрию. Варианты удлиненного додекаэдра и трапеции-ромбического додекаэдра вместе с ромбическими додекаэдрами заполняют пространство. Существует множество других додекаэдров.
Хотя додекаэдр имеет много общих черт с другими Платоновыми телами, одно их уникальное свойство состоит в том, что можно начать с угла поверхности и провести бесконечное количество прямых линий по фигуре, которые вернуться в исходную точку без пересечения любого другого угла.
Выпуклый правильный додекаэдр является одним из пяти правильных Платоновых тел и может быть представлен его символом Шлефли {5, 3}.
Двойной многогранник - это правильный икосаэдр {3, 5}, имеющий пять равносторонних треугольников вокруг каждой вершины.
 . Выпуклый правильный додекаэдр . Выпуклый правильный додекаэдр |  . Малый звездчатый додекаэдр . Малый звездчатый додекаэдр |  . Большой додекаэдр . Большой додекаэдр |  . Большой звездчатый додекаэдр . Большой звездчатый додекаэдр |
Выпуклый правильный додекаэдр также имеет три звездчатых, все из которых являются правильными звездчатыми додекаэдрами. Они образуют три из четырех многогранников Кеплера – Пуансо. Это малый звездчатый додекаэдр {5/2, 5}, большой додекаэдр {5, 5/2} и большой звездчатый додекаэдр {5 / 2, 3}. Малый звездчатый додекаэдр и большой додекаэдр двойственны друг другу; большой звездчатый додекаэдр двойственен большому икосаэдру {3, 5/2}. Все эти правильные звездчатые додекаэдры имеют правильные пятиугольные или пентаграммы грани. Выпуклый правильный додекаэдр и большой звездчатый додекаэдр - разные реализации одного и того же абстрактного правильного многогранника ; малый звездчатый додекаэдр и большой додекаэдр - разные реализации другого абстрактного правильного многогранника.
В кристаллографии два важных додекаэдра могут встречаться в виде кристаллических форм в некоторых классах симметрии кубической кристаллической системы , которые топологически эквивалентны правильному додекаэдру, но менее симметричны: пиритоэдр с пиритоэдрической симметрией и тетартоид с тетраэдрической симметрией :
| Пиритоэдр | |
|---|---|
 . У пиритоэдра 30 ребер: 6 соответствуют граням куба и 24 касаются вершин куба. . У пиритоэдра 30 ребер: 6 соответствуют граням куба и 24 касаются вершин куба. | |
| Многоугольник лица | неправильный пятиугольник |
| Диаграммы Кокстера | |
| Грани | 12 |
| Ребра | 30 (6 + 24) |
| Вершины | 20 (8 + 12) |
| Группа симметрии | Th, [4,3], (3 * 2), порядок 24 |
| Группа вращения | T, [3,3], (332), порядок 12 |
| Двойной многогранник | Псевдоикосаэдр |
| Свойства | переходная грань |
Сетка (для совершенного природного пирита).  | |
A пиритоэдр - додекаэдр с симметрией пиритоэдра (Th). Подобно правильному додекаэдру , он имеет двенадцать одинаковых пятиугольных граней, по три пересекающихся в каждой из 20 вершин (см. Рисунок). Однако пятиугольники не обязательно должны быть регулярными, и лежащее в основе атомное расположение не имеет истинной оси симметрии пятого порядка. Его 30 ребер разделены на два набора - по 24 и 6 ребер одинаковой длины. Единственные оси симметрии вращения - это три взаимно перпендикулярные оси второго порядка и четыре оси третьего порядка.
Хотя правильные додекаэдры не существуют в кристаллах, форма пиритоэдра встречается в кристаллах минерала пирита, и это может быть источником вдохновения для открытия регулярного платонового твердого тела. форма. Истинный правильный додекаэдр может иметь форму для квазикристаллов (таких как квазикристалл гольмия-магния-цинка ) с икосаэдрической симметрией, которая включает в себя истинные оси пятикратного вращения.
Его название происходит от одного из двух распространенных кристаллов, обозначенных пиритом, другой - кубом .. В пиритоэдрическом пирите грани имеют индекс Миллера из (210), что означает, что двугранный угол равен 2 · арктангенс (2) ≈ 126,87 °, и каждая пятиугольная грань имеет один угол. приблизительно 121,6 ° между двумя углами приблизительно 106,6 ° и двумя противоположными углами приблизительно 102,6 °. В идеальном кристалле размеры идеальной грани будут следующими:



Такие идеальные пропорции редко встречаются в природе.
 . Кубический пирит . Кубический пирит |  . Пиритоэдрический пирит... . Пиритоэдрический пирит... |  .... с угловыми углами .... с угловыми углами |

Если восемь вершин куба имеют координаты:
Тогда у пиритоэдра 12 дополнительных вершин:
где h - высота клиновидной «крыши» над гранями куба. Когда h = 1, шесть поперечных ребер вырождаются в точки, а пиритоэдр превращается в ромбический додекаэдр. При h = 0 поперечные ребра поглощаются гранями куба, и пиритоэдр превращается в куб. Когда h = −1 + √5 / 2, мультипликативная обратная величина золотого сечения, в результате получается правильный додекаэдр. Когда h = −1 - √5 / 2, сопряжение этого значения, результатом является правильный большой звездчатый додекаэдр. Для природного пирита h = 1/2.
   Ортогональные проекции пиритоэдра с высотой клина h = 1/2, или 1/4 длины ребра куба. Это то же самое, что и природный пирит. Эти пропорции также присутствуют в структуре Вейра – Фелана. Ортогональные проекции пиритоэдра с высотой клина h = 1/2, или 1/4 длины ребра куба. Это то же самое, что и природный пирит. Эти пропорции также присутствуют в структуре Вейра – Фелана. |   Слева h = 1/2. Справа h = 1 / φ (правильный додекаэдр). Слева h = 1/2. Справа h = 1 / φ (правильный додекаэдр). |
 Пиритоэдры в двойных положениях.
Пиритоэдры в двойных положениях. Отраженный пиритоэдр получается путем замены ненулевых координат выше. Два пиритоэдра могут быть наложены друг на друга, давая соединение двух додекаэдров. На изображении слева показан случай, когда пиритоэдры являются выпуклыми правильными додекаэдрами.
 Анимация выпуклых / вогнутых пиритоэдрических сот, между h = ± √5 - 1/2
Анимация выпуклых / вогнутых пиритоэдрических сот, между h = ± √5 - 1/2 Пиритоэдр имеет геометрическую степень свободы с предельными случаями кубического выпуклая оболочка на одном пределе коллинеарных ребер и ромбический додекаэдр в качестве другого предела, поскольку 6 ребер вырождены до нулевой длины. Правильный додекаэдр представляет собой специальный промежуточный случай, когда все ребра и углы равны.
Эти ограничивающие случаи можно обойти, создав вогнутые или невыпуклые пиритоэдры. Эндододекаэдр вогнутый и равносторонний; он может замощить пространство с помощью выпуклого правильного додекаэдра. Продолжая оттуда в этом направлении, мы переходим через вырожденный случай, когда двенадцать вершин совпадают в центре, и переходим к правильному большому звездчатому додекаэдру, где все ребра и углы снова равны, а грани искажены. в правильные пентаграммы. С другой стороны, за ромбическим додекаэдром, мы получаем невыпуклый равносторонний додекаэдр с самопересекающимися равносторонними пятиугольными гранями в форме рыбы.
| 1: 1 | 0: 1 | 1: 1 | 2: 1 | 1: 1 | 0: 1 | 1: 1 |
|---|---|---|---|---|---|---|
| h = −√5 + 1/2 | h = −1 | h = −√ 5 + 1/2 | h = 0 | h = √5 - 1/2 | h = 1 | h = √5 + 1 / 2 |
 . Правильная звезда, большой звездчатый додекаэдр, с правильными пентаграммами гранями . Правильная звезда, большой звездчатый додекаэдр, с правильными пентаграммами гранями |  . Вырожденная, 12 вершин в центре . Вырожденная, 12 вершин в центре |  . Вогнутый равносторонний додекаэдр, называемый эндододекаэдром. . Вогнутый равносторонний додекаэдр, называемый эндододекаэдром. |  . A Куб можно разделить на пиритоэдр, разделив пополам все ребра и грани в чередующихся направлениях. . A Куб можно разделить на пиритоэдр, разделив пополам все ребра и грани в чередующихся направлениях. |  . Правильный додекаэдр - это промежуточный случай с равными длинами ребер. . Правильный додекаэдр - это промежуточный случай с равными длинами ребер. |  . A ромбический додекаэдр - это вырожденный случай с 6 скрещенными элементами, уменьшенными до нулевой длины. . A ромбический додекаэдр - это вырожденный случай с 6 скрещенными элементами, уменьшенными до нулевой длины. |  . Самопересекающийся равносторонний додекаэдр . Самопересекающийся равносторонний додекаэдр |
| Тетартоид. Тетрагональный пятиугольный додекаэдр | |
|---|---|
 | |
| Многоугольник с гранями | неправильный пятиугольник |
| Нотация Конвея | gT |
| Грани | 12 |
| Ребра | 30 (6 + 12 + 12) |
| Вершины | 20 (4 + 4 + 12) |
| Группа симметрии | T, [3,3], (332), порядок 12 |
| Свойства | выпуклый, переходная грань |
 Тетартоид
Тетартоид A тетартоид (также четырехугольный пятиугольный додекаэдр, пятиугольник-тритетраэдр, и тетраэдрический пятиугольник (додекаэдр ) представляет собой додекаэдр с хиральной тетраэдрической симметрией (T). Подобно правильному додекаэдру , он имеет двенадцать одинаковых пятиугольных граней, по три пересекающихся в каждой из 20 вершин. Однако пятиугольники не правильные, и фигура не имеет осей симметрии пятого порядка.
Хотя правильные додекаэдры не существуют в кристаллах, тетартоидная форма существует. Название тетартоид происходит от греческого корня, означающего одну четверть, потому что он имеет одну четверть полной октаэдрической симметрии и половину пиритоэдрической симметрии. Минерал кобальтит может иметь эту форму симметрии.
| кобальтит |
|---|
 |
Его топология может быть в виде куба с квадратными гранями, разделенными пополам на 2 прямоугольника, таких как пиритоэдр, а затем линии биссечения наклонены, сохраняя 3 поворот сгиба по 8 углам.
Следующие точки являются вершинами четырехугольного пятиугольника при тетраэдрической симметрии :
при следующих условиях:
Его можно рассматривать как тетраэдр с ребрами, разделенными на 3 сегмента, а также с центральной точкой каждой треугольной грани. В обозначении многогранника Конвея его можно рассматривать как gT, гиротетраэдр.


 |  |  |  |
 |  |  |  |
Форма более низкой симметрии правильного додекаэдра может быть построена как двойственная многограннику, построенному из двух треугольных антикупол, соединенных основанием-к- основание, называемое треугольной гиробиантикуполой. Оно имеет симметрию D 3d, порядок 12. Оно имеет 2 набора по 3 одинаковых пятиугольника сверху и снизу, соединенных 6 пятиугольниками по бокам, которые чередуются вверх и вниз. имеет шестиугольное сечение, и идентичные копии могут быть соединены как частичные шестиугольные соты, но все верные tices не совпадают.

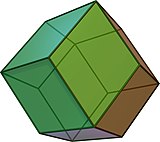 Ромбический додекаэдр
Ромбический додекаэдр Ромбический додекаэдр - это зоноэдр с двенадцатью ромбическими гранями и октаэдрической симметрией. Он двойственен квазирегулярному кубооктаэдру (архимедову твердому телу ) и встречается в природе в виде кристалла. Ромбический додекаэдр собирается вместе, заполняя пространство.
Ромбический додекаэдр можно рассматривать как вырожденный пиритоэдр, в котором 6 особых ребер уменьшены до нулевой длины, превращая пятиугольники в ромбические грани.
Ромбический додекаэдр имеет несколько звёздчатых звёзд, первая из которых также является параллелоэдром, заполняющим пространство.
Другой важный ромбический додекаэдр, Билински додекаэдр имеет двенадцать граней, соответствующих граням ромбического триаконтаэдра, то есть диагонали находятся в соотношении золотого сечения. Это также зоноэдр, описанный Билински в 1960 году. Эта фигура является еще одним заполнителем пространства, и также может встречаться в непериодических заполнениях пространства вместе с ромбическими триаконтаэдр, ромбический икосаэдр и ромбические гексаэдры.
Имеется 6 384 634 топологически различных выпуклых додекаэдра, исключая зеркальные изображения - число вершин колеблется от 8 до 20. (Два многогранника - это " топологически различные, «если они имеют внутренне различное расположение граней и вершин, так что невозможно преобразовать одну в другую, просто изменяя длину ребер или углы между ребрами или гранями.)
Топологически различные додекаэдры (исключая пятиугольную и ромбическую формы)
Арманд Спитц использовал додекаэдр в качестве эквивалента «глобуса» для своего проектора планетария с цифровым куполом. на основе предложения Альберта Эйнштейна.
| На Викискладе есть материалы, связанные с Многогранники с 12 гранями. |
| ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | ||||||||
| Треугольник | Квадрат | p-угольник | Шестиугольник | Пентагон | ||||||||
| Тетраэдр | Октаэдр • Куб | Демикуб | Додекаэдр • Икосаэдр | |||||||||
| 5-элементный | 16-элементный • Тессеракт | Демитессеракт | 24-элементный | 120-элементный • 600 ячеек | ||||||||
| 5-симплекс | 5-ортоплекс • 5-куб | 5-полукуб | ||||||||||
| 6-симплекс | 6-ортоплекс • 6-куб | 6-полукуб | 122 • 221 | |||||||||
| 7-симплекс | 7-ортоплекс • 7-куб | 7-полукуб | 132 • 231 • 321 | |||||||||
| 8-симплекс | 8-ортоплекс • 8-куб | 8-полукуб | 142 • 241 • 421 | |||||||||
| 9-симплекс | 9-ортоплекс • 9-куб | 9-демикуб | ||||||||||
| 10-симплекс | 10-ортоплекс • 10-куб | 10-demicube | ||||||||||
| n-симплекс | n-ортоплекс • n- куб | n-demicube | 1k2 • 2k1 • k21 | n-пятиугольный многогранник | ||||||||
| Темы: Семейства многогранников • Regular многогранник • Список правильных многогранников и соединений | ||||||||||||