| Demihexeract. (6-полукуб) | ||
|---|---|---|
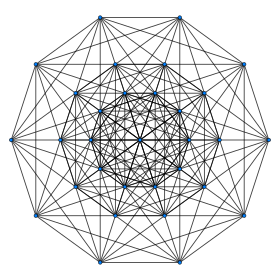 . многоугольник Петри проекция . многоугольник Петри проекция | ||
| Тип | Равномерный 6-многогранник | |
| Семейство | полугиперкуб | |
| символ Шлефли | {3,3} = h {4,3}. s {2} | |
| Диаграммы Кокстера |
| |
| Символ Кокстера | 131 | |
| 5-гранный | 44 | 12 {3} |
| 4-гранный | 252 | 60 {3} |
| Ячейки | 640 | 160 {3} |
| Лица | 640 | {3} |
| Ребра | 240 | |
| Вершины | 32 | |
| Фигура вершины | Выпрямленный 5-симплекс. | |
| Группа симметрии | D6, [3] = [1,4,3]. [2] | |
| Многоугольник Петри | десятиугольник | |
| Свойства | выпуклый | |
В геометрии 6-полукубик или полугекстерат является равномерный 6-многогранник, конструкт d из 6-куба (hexeract ) с удаленными чередующимися вершинами и. Это часть безмерно бесконечного семейства однородных многогранников, называемых полугиперкубами.
E. Л. Элте определил его в 1912 году как полуправильный многогранник, обозначив его как HM 6 для шестимерного многогранника с половинной мерой.
Кокстер назвал этот многогранник как 131из его диаграммы Кокстера, с кольцом на одной из ветвей длины 1, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() . Он может быть назван так же с помощью трехмерного экспоненциального символа Шлефли
. Он может быть назван так же с помощью трехмерного экспоненциального символа Шлефли 
Декартовы координаты вершин полугексеракта с центром в начале координат являются чередующимися половинами шестигранника :
с нечетным числом знаков плюс.
Эта матрица конфигурации представляет собой 6-полукуб. Строки и столбцы соответствуют вершинам, ребрам, граням, ячейкам, 4-граням и 5-граням. Диагональные числа говорят, сколько элементов каждого элемента встречается во всем 6-полукубе. Недиагональные числа говорят о том, сколько элементов столбца встречается в элементе строки или рядом с ним.
Числа диагонального f-вектора получаются с помощью конструкции Wythoff, делящей полный порядок группировки порядок подгрупп, удаляя по одному зеркалу.
| D6 | k-face | fk | f0 | f1 | f2 | f3 | f4 | f5 | k-figure | notes | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A4 | () | f0 | 32 | 15 | 60 | 20 | 60 | 15 | 30 | 6 | 6 | r {3,3,3,3} | D6/A4= 32 * 6! / 5! = 32 | |
| A3A1A1 | {} | f1 | 2 | 240 | 8 | 4 | 12 | 6 | 8 | 4 | 2 | {} x {3,3} | D6/A3A1A1= 32 * 6! / 4! / 2/2 = 240 | |
| A3A2 | {3} | f2 | 3 | 3 | 640 | 1 | 3 | 3 | 3 | 3 | 1 | {3} v () | D6/A3A2= 32 * 6! / 4! / 3! = 640 | |
| A3A1 | ч {4,3} | f3 | 4 | 6 | 4 | 160 | * | 3 | 0 | 3 | 0 | {3} | D6/A3A1= 32 * 6! / 4! / 2 = 160 | |
| A3A2 | {3,3} | 4 | 6 | 4 | * | 480 | 1 | 2 | 2 | 1 | {} v () | D6/A3A2= 32 * 6! / 4! / 3! = 480 | ||
| D4A1 | ч {4,3,3} | f4 | 8 | 24 | 32 | 8 | 8 | 60 | * | 2 | 0 | {} | D6/D4A1= 32 * 6! / 8/4! / 2 = 60 | |
| A4 | {3,3,3} | 5 | 10 | 10 | 0 | 5 | * | 192 | 1 | 1 | D6/A4= 32 * 6! / 5! = 192 | |||
| D5 | ч {4,3,3,3} | f5 | 16 | 80 | 160 | 40 | 80 | 10 | 16 | 12 | * | () | D6/D5= 32 * 6! / 16/5! = 12 | |
| A5 | {3,3,3,3} | 6 | 15 | 20 | 0 | 15 | 0 | 6 | * | 32 | D6/A5= 32 * 6! / 6! = 32 | |||
| плоскость Кокстера | B6 | |
|---|---|---|
| График | 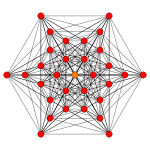 | |
| Двугранная симметрия | [12/2] | |
| Плоскость Кокстера | D6 | D5 |
| График |  | 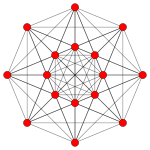 |
| Двугранная симметрия | [10] | [8] |
| Плоскость Кокстера | D4 | D3 |
| График |  | 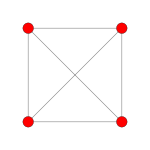 |
| Двугранная симметрия | [6] | [4] |
| Плоскость Кокстера | A5 | A3 |
| График |  | 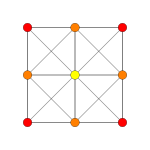 |
| Двугранная симметрия | [6] | [4] |
Имеется 47 однородных многогранников с D 6, 31 разделяются симметрией B 6, а 16 уникальны:
| многогранники D6 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 . h {4,3} . h {4,3} |  . h2{4,3} . h2{4,3} |  . h3{4,3} . h3{4,3} |  . h4{4,3} . h4{4,3} |  . h5{4,3} . h5{4,3} |  . h2,3 {4,3} . h2,3 {4,3} |  . h2,4 {4,3} . h2,4 {4,3} |  . h2,5 {4,3} . h2,5 {4,3} | ||||
 . h3,4 {4,3} . h3,4 {4,3} |  . h3,5 {4,3} . h3,5 {4,3} |  . h4,5 {4,3} . h4,5 {4,3} |  . h2,3,4 {4,3} . h2,3,4 {4,3} |  . h2,3,5 {4,3} . h2,3,5 {4,3} |  . h2,4,5 { 4,3} . h2,4,5 { 4,3} |  . h3,4,5 {4,3} . h3,4,5 {4,3} | 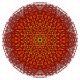 . h2,3,4,5 {4,3} . h2,3,4,5 {4,3} | ||||
6-полукуб, 1 31 является третьим в ряду размерностей однородных многогранников, выраженных Кокстером как k 31 рядов. Пятая фигура - евклидовы соты, 331, а последняя - некомпактные гиперболические соты, 4 31. Каждый прогрессивный однородный многогранник построен из предыдущего в виде его вершинной фигуры .
| n | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|
| группы Кокстера. | A3A1 | A5 | D6 | E7 |  = E 7 = E 7 |  =E7 =E7 |
| Диаграмма Кокстера. | ||||||
| Симметрия | [3] | [3] | [3] | [3] | [3] | [3] |
| Порядок | 48 | 720 | 23,040 | 2,903,040 | ∞ | |
| График |  |  |  |  | - | - |
| Название | −131 | 031 | 131 | 231 | 331 | 431 |
Также он является вторым в размерной серии однородных многогранников и соты, выраженные Coxeter как 1 3k серии. Следующая фигура - евклидовы соты 133, а последняя - некомпактные гиперболические соты, 1 34.
| Пространство | Конечное | Евклидово | Гиперболическое | |||
|---|---|---|---|---|---|---|
| n | 4 | 5 | 6 | 7 | 8 | 9 |
| Группа Кокстера. | A3A1 | A5 | D6 | E7 |  =E7 =E7 |  =E7 =E7 |
| Диаграмма Кокстера. | ||||||
| Симметрия | [3] | [3] | [3] | [3] | [[3]] | [3] |
| Заказ | 48 | 720 | 23,040 | 2,903,040 | ∞ | |
| График |  |  |  | - | - | |
| Имя | 13, -1 | 130 | 131 | 132 | 133 | |
Кокстер определил подмножество из 12 вершин, которые образуют правильный перекос икосаэдр {3, 5} с той же симметрией, что и сам икосаэдр, но под разными углами. Он назвал это правильным косым икосаэдром .
| 1 =()
| ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | ||||||||
| Треугольник | Квадрат | p-угольник | Шестиугольник | Пентагон | ||||||||
| Тетраэдр | Октаэдр • Куб | Демикуб | Додекаэдр • Икосаэдр | |||||||||
| 5-элементный | 16-элементный • Tesseract | Demitesseract | 24-элементный | 120-элементный • 600-элементный | ||||||||
| 5 -симплекс | 5-ортоплекс • 5-куб | 5-полукуб | ||||||||||
| 6-симплекс | 6-ортоплекс • 6-куб | 6 -d emicube | 122 • 221 | |||||||||
| 7-симплекс | 7-ортоплекс • 7-куб | 7-demicube | 132 • 231 • 321 | |||||||||
| 8-симплекс | 8-ортоплекс • 8- куб | 8-полукуб | 142 • 241 • 421 | |||||||||
| 9-симплекс | 9-ортоплекс • 9-куб | 9-полукуб | ||||||||||
| 10-симплекс | 10-ортоплекс • 10-куб | 10-полукуб | ||||||||||
| n-симплекс | n-ортоплекс • n- куб | n-демикуб | 1k2 • 2k1 • k21 | n-пятиугольный многогранник | ||||||||
| Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений | ||||||||||||