2₂₁многогранник - 2 21 polytope

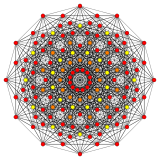. 221.	. Исправленный 2 21.
. (122 ).	. Двунаправленный 2 21. (Исправленный 1 22 ).
ортогональные проекции в E 6плоскости Кокстера

В 6-мерной геометрии многогранник 221представляет собой однородный 6-многогранник , построенный в рамках симметрии группы E6. Это было обнаружено Торольдом Госсетом, опубликованным в его статье 1900 года. Он назвал это шестигранной полурегулярной фигурой. Его также называют многогранником Шлефли.

Его символом Кокстера является 221, описывающий его раздваивающуюся диаграмму Кокстера-Дынкина с одним кольцом на конце одной из последовательностей с двумя узлами. Он также изучил его связь с 27 линиями на кубической поверхности, которые естественным образом соответствуют вершинам 2 21.

. Выпрямленное 2 21построено из точек в середине. края 221. двунаправленный 2 21построен по точкам в центрах граней треугольника 221и аналогичен выпрямленному 1 22.

. Эти многогранники являются частью семейства из 39 выпуклых однородных многогранников. в 6-мерном, состоящем из однородных граней 5-многогранника и вершинных фигур, определенных всеми перестановками колец на этой диаграмме Кокстера-Дынкина : .

• 1 2_21 Многогранник
  • 1.1 Альтернативные имена
  • 1.2 Координаты
  • 1.3 Построение
  • 1.4 Изображения
  • 1.5 Геометрическое складывание
  • 1.6 Связанные сложные многогранники
  • 1.7 Связанные многогранники
• 2 Выпрямленный многогранник 2_21
  • 2.1 Альтернативные имена
  • 2.2 Конструкция
  • 2.3 Изображения
• 3 Усеченный многогранник 2_21
  • 3.1 Изображения
• 4 См. Также
• 5 Примечания
• 6 Ссылки

221многогранник
Тип	Равномерный 6-многогранник
Семейство	k21многогранник
символ Шлефли	{3,3,3}
символ Кокстера	221
Кокстер- Диаграмма Дынкина	или
5-граней	Всего 99:. 27 211 . 72 {3}
4-гранный	648:. 432 {3} . 216 {3}
Ячейки	1080 {3,3}
Лица	720 {3}
Ребра	216
Вершины	27
Вершинная фигура	121(5-полукуб )
Многоугольник Петри	Додекагон
группа Кокстера	E6, [3], порядок 51840
Свойства	выпуклый

У 22127 вершин и 99 граней: 27 5-ортоплексов и 72 5-симплексов. Его фигура вершины представляет собой 5-полукуб.

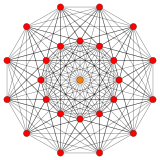
Для визуализации этот 6-мерный многогранник часто отображается в специальном наклонном ортогональном направлении проекции, которое соответствует его 27 вершинам внутри 12-угольного правильного многоугольника ( называется многоугольником Петри ). Его 216 ребер нарисованы между 2 кольцами по 12 вершин, а 3 вершины проецируются в центр. На этой проекции также можно извлекать и рисовать более высокие элементы (грани, ячейки и т. Д.).

Граф Шлефли является 1-скелетом этого многогранника.

Альтернативные имена

• E. Л. Элте назвал его V 27 (для 27 вершин) в своем списке полуправильных многогранников 1912 года.
• Icosihepta-heptacontidi-peton - 27-72 фасеточный полипетон (аббревиатура jak) (Джонатан Бауэрс)

Координаты

27 вершин могут быть выражены в 8-мерном пространстве как фигура-ребро многогранника 421 :

• (-2,0,0,0, -2,0,0,0), (0, -2,0,0, -2,0,0,0), (0,0, -2,0, -2,0,0,0), (0,0,0, -2, -2,0,0,0), (0,0,0,0, -2,0,0, -2), (0,0,0,0,0, -2, -2,0)
• (2,0,0,0, -2,0,0,0), (0,2,0,0, -2,0,0, 0), (0,0,2,0, -2,0,0,0), (0,0,0,2, -2,0,0,0), (0,0,0,0, -2,0,0,2)
• (-1, -1, -1, -1, -1, -1, -1, -1), (-1, -1, -1, 1, -1, -1, -1, 1), (-1, -1, 1, -1, -1, -1, -1, 1), (-1, -1, 1, 1, -1, -1, -1, -1), (-1, 1, -1, -1, -1, -1, -1, 1), (-1, 1, -1, 1, -1, -1, -1, -1), (-1, 1, 1, -1, -1, -1, -1, -1), (1, -1, -1, -1, -1, -1, -1, 1) (1, -1, 1, -1, -1, -1, -1, -1), (1, -1, -1, 1, -1, -1, - 1, -1) (1, 1, -1, -1, -1, -1, -1, -1), (-1, 1, 1, 1, -1, -1, -1, 1) (1, -1, 1, 1, -1, -1, -1, 1) (1, 1, -1, 1, -1, -1, -1, 1) (1, 1, 1, - 1, -1, -1, -1, 1) (1, 1, 1, 1, -1, -1, -1, -1)

Конструкция

Это s конструкция основана на группе E6.

Информация о фасете может быть извлечена из его диаграммы Кокстера-Дынкина, .

Удаление узла на короткой ветви оставляет 5-симплекс, .

Удаление узла на конце 2-длинная ветвь оставляет 5-ортоплекс в его альтернативной форме: (211), .

Каждая симплексная грань касается 5-ортоплексной грани, в то время как альтернативные грани ортоплекса касаются либо симплекса, либо еще один ортоплекс.

Число вершин определяется путем удаления окруженного узла и звонка соседнему узлу. Это делает 5-полукуб ( (121многогранник), . Ребро-фигура - это фигура вершины фигуры вершины, выпрямленного 5-ячеечного, (0 21 многогранника), .

В матрице конфигурации , количество элементов может быть получено из группы Кокстера заказов.

E6		k-face	fk	f0	f1	f2	f3	f4		f5		k-figure	notes
D5		()	f0	27	16	80	160	80	40	16	10	h {4,3,3,3}	E6/D5= 51840/1920 = 27
A4A1		{}	f1	2	216	10	30	20	10	5	5	r {3,3,3}	E6/A4A1= 51840/120/2 = 216
A2A2A1		{3}	f2	3	3	720	6	6	3	2	3	{3} x {}	E6/A2A2A1= 51840/6/6/2 = 720
A3A1		{3,3}	f3	4	6	4	1080	2	1	1	2	{} v ()	E6/A3A1= 51840/24/2 = 1080
A4		{3,3,3}	f4	5	10	10	5	432	*	1	1	{}	E6/A4= 51840/120 = 432
A4A1				5	10	10	5	*	216	0	2		E6/A4A1= 51840/120/2 = 216
A5		{3,3,3,3}	f5	6	15	20	15	6	0	72	*	()	E6/A5= 51840/720 = 72
D5		{3,3,3,4}		10	40	80	80	16	16	*	27		E6/D5= 51840 / 1920 = 27

Изображения

Вершины окрашены в соответствии с их множеством в этой проекции в прогрессивном порядке: красный, оранжевый, желтый. В скобках указано количество вершин по цвету.

плоскость Кокстера орфографические проекции

E6. [12]	D5. [8]	D4 / A2. [6]	B6. [12/2]
. (1,3)	. (1,3)	. (3,9)	. (1,3)
A5. [6]	A4. [5]	A3 / D3. [4]
. (1,3)	. (1,2)	. (1,4,7)

Геометрическое складывание

221связано в 24-ячейку путем геометрического сворачивания диаграмм Кокстера-Дынкина E6 / F4 . Это можно увидеть в проекциях плоскости Кокстера. 24 вершины 24-ячейки проецируются в те же два кольца, что и в 2 21.

E6.	F4.
. 221.	. 24-ячейке.

. Этот многогранник может тесселяции евклидова 6-пространства, образуя соты 222 с этой диаграммой Кокстера-Дынкина. : .

Связанные сложные многогранники

правильный комплексный многоугольник 3{3} 3 {3} 3, в $C\; 2\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{C\}\; ^\; \{2\}\}$имеет реальное представление как многогранник 2 21, в 4-мерном пространстве. Он называется многогранником Гессе в честь Эдмунда Гесса. Он имеет 27 вершин, 72 3-ребра и 27 3 {3} 3 грани. Его комплексная группа отражений равна 3 [3] 3 [3] 3, порядок 648.

Связанные многогранники

2 21 является четвертым в ряду измерений полуправильных многогранников. Каждый прогрессивный однородный многогранник строится вершиной фигуры предыдущего многогранника. Торольд Госсет определил эту серию в 1900 году как содержащую все фасеты регулярного многогранника, содержащие все симплексы и ортоплексы.

k21фигуры в n-мерном пространстве.
Пробел	Конечное						Евклидово	Гиперболическое
En	3	4	5	6	7	8	9	10
Кокстера. группа	E3=A2A1	E4=A4	E5=D5	E6	E7	E8	E9= $E\; ~\; 8\; \{\backslash \; displaystyle\; \{\backslash \; tilde\; \{E\}\}\; \_\; \{8\}\}$= E 8	E10= $T\; ¯\; 8\; \{\backslash \; displaystyle\; \{\backslash \; bar\; \{T\}\}\; \_\; \{8\}\}$= E 8
диаграмма Кокстера.
Симметрия	[3]	[3]	[3]	[3]	[3]	[3]	[3]	[3]
Заказ	12	120	1,920	51,840	2,903,040	696,729,600	∞
График							-	-
Название	−121	021	121	221	321	421	521	621

Многогранник 2 21 является четвертым в размерной серии 2 k2.

2k1цифр в n измерений
Пробел	Конечное						Евклидово	Гиперболическое
n	3	4	5	6	7	8	9	10
Кокстера. группа	E3=A2A1	E4=A4	E5=D5	E6	E7	E8	E9= $E\; ~\; 8\; \{\backslash \; displaystyle\; \{\backslash \; tilde\; \{E\}\; \}\; \_\; \{8\}\}$= E 8	E10= $T\; ¯\; 8\; \{\backslash \; displaystyle\; \{\backslash \; bar\; \{T\}\}\; \_\; \{8\}\}$= E 8
Coxeter. диаграмма
S симметрия	[3]	[3]	[[3]]	[3]	[3]	[3]	[3]	[3]
Заказ	12	120	384	51,840	2,903,040	696,729,600	∞
График							-	-
Название	2−1,1	201	211	221	231	241	251	261

Многогранник 2 21 является вторым в размерной серии 2 2k.

22kфигуры n измерений

Пространство	Конечное			Евклидово	Гиперболическое
n	4	5	6	7	8
группа Кокстера.	A2A2	A5	E6	$E\; ~\; 6\; \{\backslash \; displaystyle\; \{\backslash \; тильда\; \{E\}\}\; \_\; \{6\}\}$=E6	E6
диаграмма Кокстера.
График				∞	∞
Имя	22, -1	220	221	222

Выпрямленный 2 21 многогранник
Тип	равномерный 6-многогранник
символ Шлефли	t1{3,3,3}
символ Кокстера	t1(221)
диаграмма Кокстера-Дынкина	или
5-граней	126 всего: 72 t1{3} . 27 t1{3,4} . 27 t1{3,3}
4-гранный	1350
Ячейки	4320
Лица	5040
Ребра	2160
Вершины	216
Вершинная фигура	выпрямленная 5-элементная призма
группа Кокстера	E6, [3], порядок 51840
Свойства	выпуклый

У выпрямленного 2 21216 вершин и 126 граней: 72 выпрямленных 5-симплексов, и 27 ректифицированных 5-ортоплексов и 27 5-демикубов. Его вершинная фигура представляет собой выпрямленную 5-элементную призму.

Альтернативные названия

• Ректифицированный икосихепта-гептаконтиди-петон как ректифицированный 27-72 граненый полипетон (аббревиатура роджак) (Джонатан Бауэрс)

Конструкция

Его конструкция основана на E6 и информация может быть извлечена из кольцевой диаграммы Кокстера-Дынкина, представляющей этот многогранник: .

Удаление кольца на короткой ветви оставляет выпрямленный 5-симплекс, .

Удаление кольца на конце другой ветви длиной 2 оставляет выпрямленный 5-ортоплекс в его альтернативной форме: t1(211), .

Удаление кольца на конце той же ветви 2 длины оставляет 5- demicube : (121), .

Число вершин определяется удалением окруженного кольца и звонком соседнего кольца. Это делает выпрямленную 5-элементную призму, t 1 {3,3,3} x {}, .

Изображения

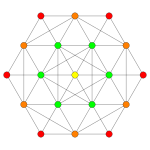
Вершины окрашиваются в соответствии с их кратностью в эта проекция в прогрессивном порядке: красный, оранжевый, желтый.

плоскость Кокстера орфографические проекции

E6. [12]	D5. [8]	D4 / A2. [6]	B6. [12/2]
A5. [6]	A4. [5]	A3 / D3. [4]

Усеченный 2 21 многогранник
Тип	Равномерный 6-многогранник
символ Шлефли	t {3,3,3}
символ Кокстера	t (2 21)
диаграмма Кокстера-Дынкина	или
5 -лицы	72 + 27 + 27
4- лица	432 + 216 + 432 + 270
Ячейки	1080 + 2160 + 1080
Лица	720 + 4320
Ребра	216 + 2160
Вершины	432
Вершинная фигура	() vr {3,3, 3}
группа Кокстера	E6, [3], порядок 51840
Свойства	выпуклый

усеченный 2 21имеет 432 вершины, 5040 ребер, 4320 граней, 1350 ячеек, и 126 4-граней. Его фигура вершины представляет собой выпрямленную пирамиду с 5 ячейками.

Изображения

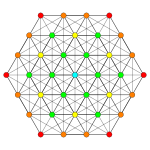
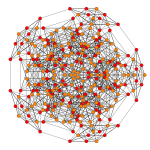
Вершины окрашены в соответствии с их множеством проекция в прогрессивном порядке: красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый.

плоскость Кокстера орфографические проекции

E6. [12]	D5. [8]	D4 / A2. [6]	B6. [12/2]
A5. [6]	A4. [5 ]	A3 / D3. [4]

• Список многогранников E6

• T. Госсет : О правильных и полурегулярных фигурах в пространстве n измерений, Вестник математики, Макмиллан, 1900
• Элте, Э.Л. (1912), Полуправильные многогранники гиперпространств, Гронинген: Университет Гронингена
• Калейдоскопы: Избранные труды HSM Коксетер, под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони С. Томпсона, Асии Ивика Вайсс, Wiley-Interscience Publication, 1995, ISBN 978-0-471- 01003-6 [1]
  • (Paper 17) Coxeter, The Evolution of Coxeter-Dynkin diagrams, [Nieuw Archief voor Wiskunde 9 (1991) 233-248] См. Рисунок 1: (стр. 232) (Узлово-реберный граф многогранника)
• Клитцинг, Ричард. «6D однородные многогранники (полипеты)».x3o3o3o3o * c3o - jak, o3x3o3o3o * c3o - rojak