| Обычный гексадекахорон. (16 ячеек). (4-ортоплекс) | |
|---|---|
 Диаграмма Шлегеля. (вершины и ребра) Диаграмма Шлегеля. (вершины и ребра) | |
| Тип | Выпуклый правильный 4-многогранник. 4-ортоплекс. 4-полукруг |
| символ Шлефли | {3,3,4} |
| Диаграмма Кокстера | |
| Ячейки | 16 {3,3} |
| Грани | 32 {3} |
| Ребра | 24 |
| Вершины | 8 |
| Вершина |  . Октаэдр . Октаэдр |
| многоугольник Петри | восьмиугольник |
| группа Кокстера | B4, [3,3,4], порядок 384. D4, порядок 192 |
| Двойной | Тессеракт |
| Свойства | выпуклый, изогональный, изотоксальный, изоэдральный, квазирегулярный |
| Равномерный индекс | 12 |
 Net
Net In четырехмерный geometry, 16-элементный - это правильный выпуклый 4-многогранник. Это один из шести правильных выпуклых 4-многогранников, впервые описанных швейцарским математиком Людвигом Шлефли в середине XIX века. Он также называется C16, гексадекахорон или гексадекаэдроид .
. Он является частью бесконечного семейства многогранников, называемых кросс-политопами или ортоплексами, и аналогичен октаэдр в трех измерениях. Это многогранник Кокстера 
Он ограничен 16 ячейками, все из которых являются правильными тетраэдрами. Он имеет 32 треугольника грани, 24 ребра и 8 вершин. 24 ребра ограничивают 6 квадратов, лежащих в 6 координатных плоскостях.
Восемь вершин 16-ячеек: (± 1, 0, 0, 0), (0, ± 1, 0, 0), (0, 0, ± 1, 0), (0, 0, 0, ± 1). Все вершины соединены ребрами, кроме противоположных пар.
символ Шлефли 16-ячеек - {3,3,4}. Его фигура вершины представляет собой правильный октаэдр. В каждой вершине пересекаются 8 тетраэдров, 12 треугольников и 6 ребер. Его фигура края представляет собой квадрат. На каждом ребре пересекаются 4 тетраэдра и 4 треугольника.
16-ячеечная ячейка может быть разложена на две одинаковые непересекающиеся круговые цепочки по восемь тетраэдров в каждой, четыре ребра в длину. Каждая цепочка в прямом растяжении образует спираль Бордейка – Кокстера. Это разложение можно увидеть в конструкции 4-4 дуоантипризмы из 16 ячеек: ![]()
![]()
![]()
![]()
![]()
![]()
![]() или
или ![]()
![]()
![]()
![]()
![]()
![]()
![]() , символ Шлефли {2} ⨂ {2} или s {2} s { 2}, симметрия 4,2,4, порядок 64.
, символ Шлефли {2} ⨂ {2} или s {2} s { 2}, симметрия 4,2,4, порядок 64.
16-ячейка может быть разделена на две октаэдрические пирамиды, которые имеют новое основание октаэдра через 16-ти клеточный центр.
Эта матрица конфигурации представляет собой 16-ячеечную матрицу. Строки и столбцы соответствуют вершинам, ребрам, граням и ячейкам. Диагональные числа говорят, сколько элементов каждого элемента встречается во всей 16 ячейке. Недиагональные числа говорят, сколько элементов столбца находится в элементе строки или рядом с ним.
 . Стереографическая проекция . Стереографическая проекция |  . 3D-проекция 16-ячеек, выполняющая простое вращение. . 3D-проекция 16-ячеек, выполняющая простое вращение. . Исходная 3D-проекция 16-ячеек. . Исходная 3D-проекция 16-ячеек. |
 . 16-ячейка имеет две конструкции Wythoff, регулярную форму и чередующуюся форму, показанные здесь как сети, причем вторая представлена попеременно двумя цветами тетраэдрических ячеек. . 16-ячейка имеет две конструкции Wythoff, регулярную форму и чередующуюся форму, показанные здесь как сети, причем вторая представлена попеременно двумя цветами тетраэдрических ячеек. |
| Плоскость Кокстера | B4 | B3/ D 4 / A 2 | B2/ D 3 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [8] | [6] | [4] |
| Плоскость Кокстера | F4 | A3 | |
| График | 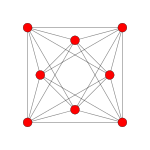 | 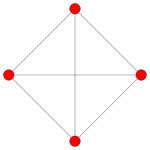 | |
| Двугранная симметрия | [12/3] | [4 ] |
Можно разбить тесселяцию 4-мерным евклидовым пространством регулярными 16 ячейками. Это называется 16-ячеечной сотой и имеет символ Шлефли {3,3,4,3}. Следовательно, 16-элементная ячейка имеет двугранный угол , равный 120 °. Каждая 16-ячейка имеет 16 соседей, с которыми она имеет общий тетраэдр, 24 соседа, с которыми она имеет только одно ребро, и 72 соседа, с которыми она имеет общую только одну точку. Двадцать четыре 16-ячейки пересекаются в любой заданной вершине этой мозаики.
Двойная тесселяция, 24-ячеечные соты, {3,4,3,3}, состоит из обычных 24-ячеек. Вместе с тессерактическими сотами {4,3,3,4} это единственные три регулярных мозаики из R.
A 16- Ячейка может быть построена из двух спиралей Бордейка – Кокстера восьми связанных тетраэдров, каждая из которых свернута в четырехмерное кольцо. 16 треугольных граней можно увидеть в двумерной сети внутри треугольной мозаики , с 6 треугольниками вокруг каждой вершины. Фиолетовые края представляют собой многоугольник Петри из 16 ячеек.

 Конверты проекции 16-ячеечной. (Каждая ячейка нарисована гранями разного цвета, перевернутые ячейки не нарисованы)
Конверты проекции 16-ячеечной. (Каждая ячейка нарисована гранями разного цвета, перевернутые ячейки не нарисованы) Параллельная проекция 16-ячеек в 3-мерном пространстве первая ячейка имеет кубический конверт. Ближайшие и самые дальние ячейки проецируются на вписанные тетраэдры внутри куба, что соответствует двум возможным способам вписать правильный тетраэдр в куб. Каждый из этих тетраэдров окружают 4 других (нерегулярных) тетраэдрических объема, которые являются образами 4 окружающих тетраэдрических ячеек, заполняя пространство между вписанным тетраэдром и кубом. Остальные 6 ячеек проецируются на квадратные грани куба. В этой проекции 16-ячейки все ее края лежат на гранях кубической оболочки.
Перспективная проекция 16-ячеек в трехмерном пространстве «первая ячейка» имеет тетраэдрическую огибающую треугольника. Расположение ячеек в этой оболочке аналогично расположению параллельной проекции ячейки первая.
Параллельная проекция 16-ячеек в 3-пространство с первой вершиной имеет октаэдрическую огибающую. Этот октаэдр можно разделить на 8 тетраэдрических объемов, разрезав его по координатным плоскостям. Каждый из этих объемов представляет собой изображение пары ячеек в 16 ячейке. Ближайшая к зрителю вершина 16-ячейки проецируется на центр октаэдра.
Наконец, параллельная проекция, обращенная к краю, имеет укороченную октаэдрическую огибающую, а параллельная проекция, обращенная сначала лицом, имеет гексагональную бипирамидальную оболочку.
Обычная проекция 16-ячеечной  и 4 пересекающихся сфер (диаграмма Венна из 4 наборов) топологически образуют тот же объект в 3D-пространстве:
и 4 пересекающихся сфер (диаграмма Венна из 4 наборов) топологически образуют тот же объект в 3D-пространстве:
 |  . .
|  . .
|  . .
|  |
Существует форма более низкой симметрии 16-ячеек, которая называется demitesseract или 4-demicube, член семейства полугиперкуба, представленный диаграммами Кокстера ![]()
![]()
![]()
![]()
![]()
![]()
![]() или
или ![]()
![]()
![]()
![]()
![]() h {4,3,3} и . Его можно нарисовать двухцветным с чередующимися тетраэдрическими ячейками.
h {4,3,3} и . Его можно нарисовать двухцветным с чередующимися тетраэдрическими ячейками.
Его также можно увидеть в форме с более низкой симметрией как тетраэдрическая антипризма, построенная из двух параллельных тетраэдров в двойных конфигурациях, соединенных 8 (возможно, удлиненными) тетраэдрами. Он представлен s {2,4,3} и диаграммой Кокстера: ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Его также можно рассматривать как пренебрежительный 4- ортотоп, представленный s {2}, и диаграммой Кокстера: ![]()
![]()
![]()
![]()
![]()
![]()
![]() или
или ![]()
![]()
![]()
![]()
![]() .
.
С тессерактом, построенным как дуопризма 4-4 , 16-ячеечная может рассматриваться как двойная, дуопирамида 4-4 .
| Имя | Диаграмма Кокстера | Символ Шлефли | Нотация Кокстера | Порядок | Вершинная фигура |
|---|---|---|---|---|---|
| Обычная 16-ячеечная | {3,3,4} | [ 3,3,4] | 384 | ||
| Demitesseract. Quasiregular 16-cell | h {4,3,3}. {3,3} | [3] = [1,4,3,3] | 192 | ||
| Чередование 4-4 дуопризма | 2s {4,2,4} | [[[4,2,4 Превосходно] ] | 64 | ||
| Тетраэдрическая антипризма | с {2,4,3} | [2,4,3] | 48 | ||
| Переменная квадратная призматическая призма | sr {2,2,4} | [(2,2),4 убедительно | 16 | ||
| Snub 4 - ортотоп | s {2} | [2,2,2] = [2] | 8 | ||
| 4-fusil | |||||
| {3,3,4} | [ 3,3,4] | 384 | |||
| {4} + {4} или 2 {4} | [[4,2,4]] = [8,2,8 ] | 128 | |||
| {3,4} + {} | [4,3,2] | 96 | |||
| {4} +2 {} | [4,2,2 ] | 32 | |||
| {} + {} + {} + {} или 4 {} | [2,2,2 impression | 16 |
Многоугольник Мебиуса – Кантора - это правильный комплексный многоугольник 3{3} 3, ![]()
![]()
![]() в
в 
Правильный комплексный многоугольник, 2 {4} 4, ![]()
![]()
![]() , в
, в 
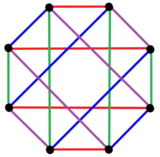 . В B 4плоскости Кокстера, 2{4} 4 имеет 8 вершин и 16 2-ребер, показанных здесь с 4 наборами цветов. . В B 4плоскости Кокстера, 2{4} 4 имеет 8 вершин и 16 2-ребер, показанных здесь с 4 наборами цветов. |  . 8 вершин сгруппированы в 2 набора (показаны красным и синим), каждый из которых соединен ребрами только с вершинами в другом наборе, что делает этот многоугольник полным двудольным графом, K 4, 4. . 8 вершин сгруппированы в 2 набора (показаны красным и синим), каждый из которых соединен ребрами только с вершинами в другом наборе, что делает этот многоугольник полным двудольным графом, K 4, 4. |
Обычные 16-ячейковые вместе с тессерактом существуют в наборе из 15 однородных 4-многогранников с одинаковой симметрией. Он также является частью однородных многогранников симметрии D 4.
Этот 4-многогранник также связан с кубическими сотами, додекаэдром четвертого порядка. соты и гексагональные мозаичные соты четвертого порядка, которые все имеют восьмигранные фигуры вершин.
Это находится в последовательности до трех правильных 4-многогранников : 5-ячеечная {3,3,3}, 600-ячеечная {3,3,5} евклидова четырехмерного пространства и порядок. -6 тетраэдрических сот {3,3,6} гиперболического пространства. Все они имеют тетраэдрические ячейки.
Он является первым в последовательности квазирегулярных многогранников и сот h {4, p, q} и последовательности полусимметрии для регулярных форм {p, 3,4}.
| ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| An | Bn | I2( p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | ||||||||
| Треугольник | Квадрат | p-угольник | Шестиугольник | Пентагон | ||||||||
| Тетраэдр | Октаэдр • Куб | Демикуб | Додекаэдр • Икосаэдр | |||||||||
| 5-элементный | 16-элементный • Тессеракт | Димитессеракт | 24-элементный | 120-элементный • 600 ячеек | ||||||||
| 5-симплекс | 5-ортоплекс • 5-куб | 5-полукуб | ||||||||||
| 6-симплекс | 6-ортоплекс • 6-куб | 6-полукуб | 122 • 221 | |||||||||
| 7-симплекс | 7-ортоплекс • 7-куб | 7-полукуб | 132 • 231 • 321 | |||||||||
| 8-симплекс | 8-ортоплекс • 8-куб | 8-полукуб | 142 • 241 • 421 | |||||||||
| 9-симплекс | 9-ортоплекс • 9-куб | 9-полукуб | ||||||||||
| 10-симплекс | 10-ортоплекс • 10-куб | 10-полукуб | ||||||||||
| n-симплекс | n-ортоплекс • n- куб | n-полукуб | 1k2 • 2k1 • k21 | n-пятиугольный многогранник | ||||||||
| Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений | ||||||||||||