Октаэдр

Многогранник с 8 гранями

Правильный октаэдр
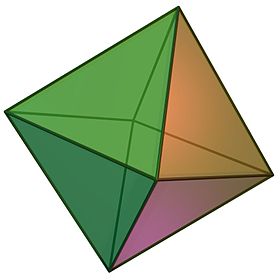. (Нажмите здесь, чтобы повернуть модель)
Тип	Платоново твердое тело
Элементы	F = 8, E = 12. V = 6 (χ = 2)
Грани по сторонам	8 {3}
Обозначение Конвея	O. aT
символы Шлефли	{3,4}
	r {3,3} или $\{3\; 3\}\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{Bmatrix\}\; 3\; \backslash \backslash \; 3\; \backslash \; end\; \{Bmatrix\}\}\}$
Конфигурация лица	V4.4.4
Символ Wythoff	4 | 2 3
Диаграмма Кокстера
Симметрия	Oh, BC 3, [4,3], (* 432)
Группа вращения	O, [4,3], ( 432)
Ссылки	U 05, C 17, W 2
Свойства	правильный, выпуклый дельтаэдр
Двугранный угол	109,47122 ° = arccos (- ⁄ 3)
. 3.3. 3.3. (Вершинная фигура )	. Куб. (двойной многогранник )
. Сеть

3D модель правильного октаэдра.

В геометрии октаэдр (множественное число: октаэдры) - это многогранник с восемью гранями, двенадцатью ребрами и шестью вершинами. Этот термин чаще всего используется для обозначения правильного октаэдра, a Платоново тело, состоящее из восьми равносторонних треугольников, четыре из которых пересекаются в каждой вершине .

Правильный октаэдр - это двойственный многогранник куба . Это выпрямленный тетраэдр. Это квадратная бипирамида в любой из трех ортогональных ориентаций. Это также треугольник антипризма в любой из четырех ориентаций.

Октаэдр является трехмерным случаем более общей концепции перекрестного многогранника .

Правильный октаэдр - это 3-шар в Манхэттене (ℓ 1) метрика.

Содержание

• 1 Правильный октаэдр
  • 1.1 Размеры
  • 1.2 Ортогональные проекции
  • 1.3 Сферическая мозаика
  • 1.4 Декартовы координаты
  • 1.5 Площадь и объем
  • 1.6 Геометрические соотношения
  • 1.7 Однородные раскраски и симметрия
  • 1.8 Сети
  • 1.9 Двойные
  • 1.10 Огранка
• 2 Неправильные октаэдры
  • 2.1 Другие выпуклые октаэдры
• 3 Октаэдры в физическом мире
  • 3.1 Октаэдры в природе
  • 3.2 Октаэдры в искусстве и культуре
  • 3.3 Тетраэдрическая ферма
• 4 Родственные многогранники
  • 4.1 Тетратетраэдр
  • 4.2 Тригональная антипризма
  • 4.3 Квадратная бипирамида
• 5 См. Также
• 6 Ссылки
• 7 Внешние ссылки

Правильный октаэдр

Размеры

Если длина ребра правильного октаэдра равна a, радиус описанной сферы (тот, который касается октаэдра в все вершины) равно

$ru\; =\; 2\; 2\; a\; \approx \; 0,707\; \cdot \; a\; \{\backslash \; displaystyle\; r\_\; \{u\}\; =\; \{\backslash \; frac\; \{\backslash \; sqrt\; \{2\}\}\; \{2\}\}\; a\; \backslash \; приблизительно\; 0,707\; \backslash \; cdot\; a\}$

и радиус вписанной сферы (касательная к каждой из граней октаэдра) равен

$ri\; =\; 6\; 6\; a\; \approx \; 0,408\; \cdot \; a\; \{\backslash \; displaystyle\; r\_\; \{i\}\; =\; \{\backslash \; frac\; \{\backslash \; sqrt\; \{6\; \}\}\; \{6\}\}\; a\; \backslash \; приблизительно\; 0,408\; \backslash \; cdot\; a\}$

, а средний радиус, который касается середины каждого края, равен

$rm\; =\; 1\; 2\; a\; =\; 0,5\; \cdot \; a\; \{\backslash \; displaystyle\; r\_\; \{m\}\; =\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; a\; =\; 0.5\; \backslash \; cdot\; a\}$

Ортогональные проекции

Октаэдр имеет четыре специальных ортогональных проекции, центрированных на ребре, вершине, лицо и нормально к лицу. Вторая и третья соответствуют плоскостям Кокстера B 2 и A 2.

Ортогональные проекции

по центру	Edge	Face. Normal	Вершина	Лицо
Изображение
Проективная. симметрия	[2]	[2]	[4]	[6]

Сферическая мозаика

Октаэдр также может быть представлен как сферическая мозаика и спроецирован на плоскость с помощью стереографическая проекция. Эта проекция конформна, сохраняя углы, но не площади или длины. Прямые на сфере проектируются как дуги окружности на плоскость.

Ортографическая проекция	Стереографическая проекция

Декартовы координаты

Октаэдр с длиной ребра √2 может быть размещен так, чтобы его центр находился в начале координат, а его вершины - на осях координат; тогда декартовы координаты вершин равны

(± 1, 0, 0);

(0, ± 1, 0);

(0, 0, ± 1).

В декартовой системе координат x – y – z октаэдр с центром , координатами (a, b, c) и радиусом r является множеством всех точек (x, y, z) таких, что

$|\; х\; -\; а\; |\; +\; |\; у\; -\; б\; |\; +\; |\; z\; -\; c\; |\; =\; r.\; \{\backslash \; displaystyle\; \backslash \; left\; |\; xa\; \backslash \; right\; |\; +\; \backslash \; left\; |\; yb\; \backslash \; right\; |\; +\; \backslash \; left\; |\; zc\; \backslash \; right\; |\; =\; r.\}$

Площадь и объем

Площадь поверхности A и объем V правильного октаэдра с длиной ребра a:

$A\; =\; 2\; 3\; a\; 2\; \approx \; 3,464\; a\; 2\; \{\backslash \; displaystyle\; A\; =\; 2\; \{\backslash \; sqrt\; \{3\}\}\; a\; ^\; \{2\}\; \backslash \; приблизительно\; 3,464\; a\; ^\; \{2\}\}$

$V\; =\; 1\; 3\; 2\; a\; 3\; \approx \; 0,471\; a\; 3\; \{\backslash \; displaystyle\; V\; =\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; \{\backslash \; sqrt\; \{2\}\}\; a\; ^\; \{3\}\; \backslash \; приблизительно\; 0,471\; a\; ^\; \{3\}\}$

Таким образом, объем в четыре раза больше, чем у правильного тетраэдра с той же длиной ребра, а площадь поверхности в два раза (потому что у нас 8, а не 4 треугольника).

Если октаэдр был растянут так, что он подчиняется уравнению

$|\; х\; х\; м\; |\; +\; |\; г\; г\; м\; |\; +\; |\; z\; z\; m\; |\; =\; 1,\; \{\backslash \; displaystyle\; \backslash \; left\; |\; \{\backslash \; frac\; \{x\}\; \{x\_\; \{m\}\}\}\; \backslash \; right\; |\; +\; \backslash \; left\; |\; \{\backslash \; frac\; \{y\}\; \{y\_\; \{m\}\}\}\; \backslash \; right\; |\; +\; \backslash \; left\; |\; \{\; \backslash \; frac\; \{z\}\; \{z\_\; \{m\}\}\}\; \backslash \; right\; |\; =\; 1,\}$

формулы для площади поверхности и объема расширяются до

$A\; =\; 4\; xmymzm\; \times \; 1\; xm\; 2\; +\; 1\; ym\; 2\; +\; 1\; zm\; 2,\; \{\backslash \; displaystyle\; A\; =\; 4\; \backslash ,\; x\_\; \{m\}\; \backslash ,\; y\_\; \{m\}\; \backslash ,\; z\_\; \{m\}\; \backslash \; times\; \{\backslash \; sqrt\; \{\{\backslash \; frac\; \{1\}\; \{x\_\; \{m\}\; ^\; \{2\}\}\})\; +\; \{\backslash \; frac\; \{1\}\; \{y\_\; \{m\}\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{z\_\; \{m\}\; ^\; \{2\}\}\}\}\},\}$

$V\; =\; 4\; 3\; xmymzm.\; \{\backslash \; displaystyle\; V\; =\; \{\backslash \; frac\; \{4\}\; \{3\}\}\; \backslash ,\; x\_\; \{m\}\; \backslash ,\; y\_\; \{m\}\; \backslash ,\; z\_\; \{m\}.\}$

Кроме того, тензор инерции вытянутого октаэдра равен

$I\; =\; [1\; 10\; m\; (ym\; 2\; +\; zm\; 2)\; 0\; 0\; 0\; 1\; 10\; m\; (xm\; 2\; +\; zm\; 2)\; 0\; 0\; 0\; 1\; 10\; m\; (xm\; 2\; -\; ym\; 2)].\; \{\backslash \; displaystyle\; I\; =\; \{\backslash \; begin\; \{bmatrix\}\; \{\backslash \; frac\; \{1\}\; \{10\}\}\; m\; (y\_\; \{m\}\; ^\; \{2\}\; +\; z\_\; \{m\}\; ^\; \{2\})\; 0\; 0\; \backslash \backslash \; 0\; \{\backslash \; frac\; \{1\; \}\; \{10\}\}\; m\; (x\_\; \{m\}\; ^\; \{2\}\; +\; z\_\; \{m\}\; ^\; \{2\})\; 0\; \backslash \backslash \; 0\; 0\; \{\backslash \; frac\; \{1\}\; \{10\}\}\; m\; (x\_\; \{m\}\; ^\; \{2\}\; -\; y\_\; \{m\}\; ^\; \{2\})\; \backslash \; end\; \{bmatrix\}\}.\}$

Они сводятся к уравнениям для правильного октаэдра, когда

$xm\; =\; ym\; =\; zm\; =\; a\; 2\; 2.\; \{\backslash \; displaystyle\; x\_\; \{m\}\; =\; y\_\; \{m\}\; =\; z\_\; \{m\}\; =\; a\; \backslash ,\; \{\backslash \; frac\; \{\backslash \; sqrt\; \{2\}\}\; \{2\}\}.\}$

Геометрические соотношения

Октаэдр представляет центральный пересечение двух тетраэдров

Внутренняя часть соединения двух двойных тетраэдров представляет собой октаэдр, и это соединение, называемое stella octangula, является его первым и только звездочка. Соответственно, правильный октаэдр является результатом отсечения от правильного тетраэдра четырех правильных тетраэдров половинного линейного размера (то есть выпрямления тетраэдра). Вершины октаэдра лежат в серединах ребер тетраэдра, и в этом смысле он относится к тетраэдру так же, как кубооктаэдр и икосододекаэдр относятся к другому. Платоновы тела. Также можно разделить ребра октаэдра в соотношении золотой середины, чтобы определить вершины икосаэдра. Это делается путем размещения векторов по краям октаэдра таким образом, чтобы каждая грань была ограничена циклом, а затем аналогичным образом разбивая каждое ребро на золотую середину в направлении его вектора. Есть пять октаэдров, которые определяют любой данный икосаэдр таким образом, и вместе они определяют правильное соединение.

Октаэдры и тетраэдры можно чередовать, чтобы сформировать однородную по вершинам, ребрам и граням мозаику пространства, названную октетной фермой Бакминстером Фуллером. Это единственная такая мозаика, за исключением регулярной мозаики кубов, и одна из 28 выпуклых однородных сот. Другой - мозаика из октаэдров и кубооктаэдров.

Октаэдр уникален среди Платоновых тел тем, что имеет четное количество граней, пересекающихся в каждой вершине. Следовательно, это единственный член этой группы, у которого есть зеркальные плоскости, которые не проходят ни через одну из граней.

Используя стандартную номенклатуру для тел Джонсона, октаэдр будет называться квадратной бипирамидой. Усечение двух противоположных вершин приводит к квадратному двузубцу.

Октаэдр 4-связный, что означает, что для разъединения оставшихся вершин требуется удаление четырех вершин. Это один из четырех четырехсвязных симплициальных хорошо покрытых многогранников, что означает, что все максимальные независимые множества его вершин имеют одинаковый размер. Три других многогранника с этим свойством: пятиугольная дипирамида , курносый дифеноид и неправильный многогранник с 12 вершинами и 20 треугольными гранями.

Октаэдр также может может быть сгенерирован как в случае 3D суперэллипсоида со всеми значениями, установленными на 1.

Равномерная окраска и симметрия

Имеется 3 однородных окраски октаэдр, названный цветами треугольных граней, окружающих каждую вершину: 1212, 1112, 1111.

Группа симметрии октаэдра - O h порядка 48, трехмерная гипероктаэдрическая группа. Подгруппы этой группы включают D 3d (порядок 12), группу симметрии треугольной антипризмы ; D4h(порядок 16), группу симметрии квадрата бипирамида ; и T d (порядок 24), группа симметрии выпрямленного тетраэдра. Эти симметрии можно подчеркнуть разной окраской лиц.

Имя	Октаэдр	Ректифицированный тетраэдр. (Тетратетраэдр)	Треугольная антипризма	Квадратная бипирамида	Ромбический фузиль
Изображение. (Раскраска лица)	. (1111)	. (1212)	. (1112)	. (1111)	. (1111)
Коксетер диаграмма		=	.
символ Шлефли	{3,4}	r {3,3}	s {2,6}. sr {2,3}	футов {2,4}. {} + {4}	ftr {2,2}. {} + {} + {}
символ Wythoff	4 | 3 2	2 | 4 3	2 | 6 2. | 2 3 2
Симметрия	Oh, [4,3], (* 432)	Td, [3,3], (* 332)	D3d, [2,6], (2 * 3). D3, [2,3], (322)	D4h, [2,4], (* 422)	D2h, [2,2], (* 222)
Заказ	48	24	12. 6	16	8

Сети

Он имеет одиннадцать расположений сетей.

Двойной

Октаэдр - это двойной многогранник к кубу .

Если длина ребра октаэдра $=\; a\; \{\backslash \; displaystyle\; =\; a\}$, то длина ребра двойного куба $=\; 2\; a\; \{\backslash \; displaystyle\; =\; \{\backslash \; sqrt\; \{2\}\}\; a\}$.

Огранка

Равномерный тетрагемигексаэдр представляет собой тетраэдрическую симметрию огранку правильного октаэдра, разделяющего ребро и расположение вершин. У него четыре треугольных грани и три центральных квадрата.

. Октаэдр

. Тетрагемигексаэдр

Неправильные октаэдры

Следующие многогранники комбинаторно эквивалентны правильному многограннику. Все они имеют шесть вершин, восемь треугольных граней и двенадцать ребер, которые однозначно соответствуют характеристикам правильного октаэдра.

• Треугольные антипризмы : две грани равносторонние, лежат в параллельных плоскостях и имеют общую ось симметрии. Остальные шесть треугольников равнобедренные.
• Тетрагональные бипирамиды, в которых по крайней мере один из экваториальных четырехугольников лежит на плоскости. Правильный октаэдр - это особый случай, когда все три четырехугольника являются плоскими квадратами.
• Многогранник Шёнхардта, невыпуклый многогранник, который нельзя разбить на тетраэдры без введения новых вершин.
• Октаэдр Брикара, невыпуклый самопересекающийся гибкий многогранник

Другие выпуклые октаэдры

В более общем смысле октаэдром может быть любой многогранник с восемью гранями. Правильный октаэдр имеет 6 вершин и 12 ребер, минимум для октаэдра; неправильные октаэдры могут иметь до 12 вершин и 18 ребер. Всего существует 257 топологически различных выпуклых октаэдров, исключая зеркальные изображения. Более конкретно, существует 2, 11, 42, 74, 76, 38, 14 для октаэдров с 6–12 вершинами соответственно. (Два многогранника являются «топологически разными», если они имеют внутренне различное расположение граней и вершин, так что невозможно преобразовать один в другой, просто изменяя длину ребер или углы между ребрами или гранями.)

Некоторые более известные неправильные октаэдры включают следующее:

• Гексагональная призма : две грани - параллельные правильные шестиугольники; шесть квадратов соединяют соответствующие пары ребер шестиугольника.
• Гептагональная пирамида : одна грань представляет собой семиугольник (обычно правильный), а остальные семь граней - треугольники (обычно равнобедренные). Невозможно, чтобы все треугольные грани были равносторонними.
• Усеченный тетраэдр : четыре грани тетраэдра усекаются, чтобы стать правильными шестиугольниками, и есть еще четыре грани равностороннего треугольника, где каждая вершина тетраэдра была усечена.
• Тетрагональный трапецоэдр : восемь граней - конгруэнтные воздушные змеи.

Октаэдры в физическом мире

Октаэдры в природе

Флюорит октаэдр.

• Природные кристаллы алмаз, квасцы или флюорит обычно октаэдрические, так как заполняющие пространство тетраэдрически-октаэдрические соты.
• пластины камасита сплава в октаэдрите метеоритах расположены параллельно восьми граням октаэдра.
• Многие ионы металлов координируют шесть лигандов в октаэдре или искаженная октаэдрическая конфигурация.
• Узоры Видманштеттена в кристаллах никеля -железа

Октаэдры в искусстве и культуре

Две идентичности образно сформированные змеи рубика могут приближаться к октаэдру.

• Особенно в ролевых играх это твердое тело известно как «d8», одна из наиболее распространенных многогранных игральных костей.
• Если каждое ребро октаэдра заменить резистором Ом , сопротивление между противоположными вершинами составит 1/2 Ом, а сопротивление между соседними вершинами - 5/12 Ом.
• Шесть музыкальных нот могут быть расположены на вершинах октаэдра таким образом, что каждое ребро представляет диаду согласных, а каждая грань представляет собой триаду согласных; см. гексани.

Тетраэдрическая ферма

Каркас из повторяющихся тетраэдров и октаэдров был изобретен Бакминстером Фуллером в 1950-х годах и известен как пространственный каркас, обычно считается самой прочной конструкцией для сопротивления консольным напряжениям.

Родственные многогранники

Правильный октаэдр может быть увеличен до тетраэдра путем добавления 4 тетраэдров на чередующихся гранях. Добавление тетраэдров ко всем 8 граням создает звездчатый октаэдр.

тетраэдр	звездчатый октаэдр

Октаэдр является одним из семейства однородных многогранников, связанных с кубом.

Однородные октаэдрические многогранники
Симметрия : [4,3], (* 432)							[4,3]. (432)	[1, 4,3] = [3,3]. (* 332)		[3,4]. (3 * 2)
{4,3}	t {4,3}	r {4,3}. r {3}	t{3,4}. t {3}	{3, 4}. {3}	rr {4,3}. s2{3,4}	tr {4,3}	sr {4,3}	h {4,3}. {3,3}	h2{4,3}. t {3,3}	с {3,4}. s {3}
		. =	. =	. =				=. или	=. или	=.
		.	.	.	.					.
Двойники к однородным многогранникам
V4	V3.8	V (3.4)	V4.6	V3	V3.4	V4. 6.8	V3.4	V3	V3.6	V3

Это также один из простейших примеров гиперсимплекса, многогранника, образованного определенными пересечениями гиперкуба с a гиперплоскость.

Октаэдр топологически связан как часть последовательности правильных многогранников с символами Шлефли {3, n}, продолжающихся в гиперболической плоскости.

* n32 симметрии мутация правильных мозаик: {3, n} [ v ]
Сферический				Евклид.	Компактный гипер.		Парако.	Некомпактный гиперболический
3.3	3	3	3	3	3	3	3	3	3	3	3

Тетратетраэдр

Правильный октаэдр также можно считать выпрямленным тетраэдром - и его можно назвать тетраэтраэдром. Это можно показать на двухцветной модели лица. При такой раскраске октаэдр имеет тетраэдрическую симметрию.

Сравните эту последовательность усечения между тетраэдром и его двойником:

Семейство однородных тетраэдрических многогранников
Симметрия : [3,3], (* 332)							[3,3], (332)
{3,3}	t {3,3}	r {3,3}	t {3,3}	{3,3}	rr {3,3}	tr {3,3}	sr {3,3}
Дублирует однородные многогранники
V3.3.3	V3.6.6	V3.3.3.3	V3.6.6	V3.3.3	V3.4.3.4	V4.6.6	V3.3.3.3.3

Вышеупомянутые формы также могут быть реализованы как срезы, ортогональные длинной диагонали тессеракта . Если эта диагональ ориентирована вертикально с высотой 1, то первые пять вышеприведенных срезов располагаются на высотах r, 3/8, 1/2, 5/8 и s, где r - любое число в диапазоне 0 < r ≤ 1/4, and s is any number in the range 3/4 ≤ s < 1.

Октаэдр как тетратетраэдр существует в последовательности симметрий квазирегулярных многогранников и мозаик с конфигурациями вершин (3.n), переходящих от мозаик сферы к евклидовой плоскости и в гиперболическую плоскость. С орбифолдной нотацией симметрией * n32 все эти мозаики являются конструкциями Витхоффа в пределах фундаментальной области симметрии, с образующими точками в правом углу области.

* n32 орбифолдные симметрии квазирегулярных мозаик : (3.n)
. Конструкция	Сферическая			евклидова	гиперболическая
	* 332	* 432	* ​​532	* ​​632	* ​​732	* ​​832...	* ​​∞32
Квазирегулярный. цифры
Вертекс	(3,3)	(3,4)	(3,5)	(3,6)	(3,7)	(3,8)	(3. ∞)

Тригональная антипризма

Как тригональная антипризма, октаэдр относится к семейству гексагональной двугранной симметрии.

Равномерные шестиугольные двугранные сферические многогранники
Симметрия : [6,2], (* 622)							[6,2], (622)	[6,2], (2 * 3)
{6,2}	t {6,2}	r {6,2}	t {2,6}	{2,6}	rr {6,2}	tr {6,2}	sr {6,2}	s {2,6}
От двойного к униформе
V6	V12	V6	V4.4.6	V2	V4.4.6	V4.4.12	V3.3.3.6	V3.3.3.3

Семейство унифицированных n-угольных антипризм [ v ]
Изображение многогранника												...	Апейрогональная антипризма
Сферическое мозаичное изображение												Плоское мозаичное изображение
Конфигурация вершины n.3.3.3	2.3.3.3	3.3.3.3	4.3.3.3	5.3.3.3	6.3.3.3	7.3.3.3	8.3.3.3	9.3.3.3	10.3.3.3	11.3.3.3	12.3.3.3	...	∞.3.3.3

Квадратная бипирамида

Семейство бипирамид

Многогранник
Кокстера
Мозаика
Конфигурация		V3.4.4	V4.4.4	V5.4.4	V6.4.4	V7.4.4	V8.4.4	V9.4.4	V10.4.4

См. Также

• Октаэдрическое число
• Центрированное октаэдрическое число
• Вращающееся октаэдрическое число ron
• Stella octangula
• Октаэдр Triakis
• Hexakis octahedron
• Усеченный октаэдр
• Octaэдрическая геометрия молекулы
• Октаэдрическая симметрия
• Октаэдрический граф
• Октаэдрическая сфера

Ссылки

Внешние ссылки

• «Октаэдр». Encyclopædia Britannica. 19(11-е изд.). 1911.
• Вайсштейн, Эрик У. «Октаэдр». MathWorld.
• Клитцинг, Ричард. "3D выпуклые однородные многогранники x3o4o - oct".
• Редактируемая печатная сетка октаэдра с интерактивным трехмерным представлением
• Бумажная модель октаэдра
• K.J.M. Маклин, Геометрический анализ пяти платоновых тел и других полурегулярных многогранников
• Однородные многогранники
• Многогранники виртуальной реальности Энциклопедия многогранников
  • Нотация Конвея для многогранников Попробуйте: dP4

v t Фундаментальный выпуклый правильный и равномерный многогранник в размерностях 2–10
An	Bn	I2(p) / Dn	E6 / E7 / E8 / F4 / G2	Hn
Треугольник	Квадрат	p-угольник	Шестиугольник	Пентагон
Тетраэдр	Октаэдр • Куб	Демикуб		Додекаэдр • Икосаэдр
5-элементный	16-элементный • Tesseract	Demitesseract	24-элементный	120-элементный • 600-элементный
5-симплексный	5-ортоплексный • 5-куб	5-полукуб
6-симплекс	6-ортоплекс • 6-куб	6-полукуб	122 • 221
7-симплекс	7-ортоплекс • 7-куб	7-полукуб	132 • 231 • 321
8-симплекс	8-ортоплекс • 8-куб	8-полукуб	142 • 241 • 421
9-симплекс	9-ортоплекс • 9-куб	9-полукуб
10-симплекс	10-ортоплекс • 10-куб	10-демикуб e
n-симплекс	n-ортоплекс • n- куб	n-полукуб	1k2 • 2k1 • k21	n-пятиугольный многогранник
Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и составных частей