9-demicube - 9-demicube

Демиеннеракт. (9-полукруг)
. многоугольник Петри
Тип	Унифицированный 9-многогранник
Семейство	полугиперкуб
Символ Кокстера	161
Символ Шлефли	{3,3} = h {4,3}. s {2}
Диаграмма Кокстера-Дынкина	= .
8-граней	274	18 {3} . 256 {3}
7-faces	2448	144 {3} . 2304 {3}
6- лиц	9888	672 {3} . 9216 {3}
5- лица	23520	2016 {3} . 21504 {3}
4-faces	36288	4032 {3} . 32256 {3}
Ячейки	37632	5376 {3} . 32256 {3, 3}
Грани	21504	{3}
Ребра	4608
Вершины	256
Вершина	Выпрямленный 8-симплекс.
Группа симметрии	D9, [3] = [1,4,3]. [2]
Двойные	?
Свойства	выпуклый

В геометрии, demienneract или 9-demicube - это однородный 9-многогранник, построенный из 9-куба, с h чередующиеся вершины удалены. Он является частью безмерно бесконечного семейства однородных многогранников, называемых полугиперкубами.

E. Л. Элте определил его в 1912 г. как полуправильный многогранник, обозначив его как HM 9 для 9-мерного многогранника половинной меры.

Кокстер назвал этот многогранник 161из его диаграммы Кокстера с кольцом на одной из ветвей длины 1, и символом Шлефли $\{3\; 3,\; 3,\; 3,\; 3,\; 3,\; 3\; 3\}\; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; \{3\; \{\backslash \; begin\; \{array\}\; \{l\}\; 3,3,3,3,3,3\; \backslash \backslash \; 3\; \backslash \; end\; \{array\}\}\; \backslash \; right\; \backslash \}\}$или {3,3}.

• 1 Декартовы координаты
• 2 Изображения
• 3 Ссылки
• 4 Внешние ссылки

Декартовы координаты для вершин полумесяца с центром в начале координат: чередующиеся половины объединяют :

(± 1, ± 1, ± 1, ± 1, ± 1, ± 1, ± 1, ± 1, ± 1)

с нечетным числом знаков плюс.

орфографические проекции

плоскость Кокстера	B9	D9	D8
График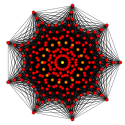
Двугранная симметрия	[18] = [9]	[16]	[14]
График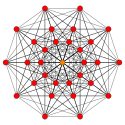
Плоскость Кокстера	D7	D6
Двугранная симметрия	[12]	[10]
Группа Кокстера	D5	D4	D3
График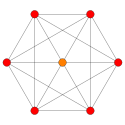
Двугранная симметрия	[8]	[6]	[4]
Плоскость Кокстера	A7	A5	A3
График
Двугранная симметрия	[8]	[6]	[4]

• HSM Coxeter :
  • Coxeter, Regular Polytopes, (3-е издание, 1973 г.), Dover edition, ISBN 0-486-61480-8, стр. 296, Таблица I (iii): Правильные многогранники, три правильных многогранника в n-мерном пространстве (n≥5)
  • H.S.M. Кокстер, Регулярные многогранники, 3-е издание, Довер, Нью-Йорк, 1973, с. 296, Таблица I (iii): Правильные многогранники, три правильных многогранника в n-мерном пространстве (n≥5)
  • Калейдоскопы: Избранные сочинения Х.С.М. Кокстер, под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони С. Томпсона, Асии Ивика Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471- 01003-6 [1]
    • (Документ 22) HSM Кокстер, Правильные и полурегулярные многогранники I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Документ 23) H.S.M. Кокстер, Правильные и полурегулярные многогранники II, [Math. Zeit. 188 (1985) 559-591]
    • (Документ 24) H.S.M. Кокстер, Правильные и полурегулярные многогранники III, [Math. Zeit. 200 (1988) 3-45]
• Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Страсс, Симметрии вещей 2008, ISBN 978-1- 56881-220-5 (Глава 26. стр. 409: Hemicubes: 1 n1)
• Klitzing, Richard. «9D однородные многогранники (polyyotta) x3o3o * b3o3o3o3o3o3o - henne».

• Ольшевский, Джордж. "Demienneract". Глоссарий по гиперпространству. Архивировано из оригинального 4 февраля 2007 года. В цитировании отсутствует неизвестный параметр: | 1 =()
• Многомерный глоссарий