 . 122. . 122. |  . Исправленный 1 22. . Исправленный 1 22. | 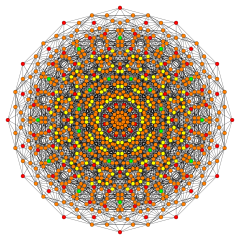 . Двунаправленный 1 22. . Двунаправленный 1 22. |
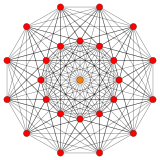 . 221. . 221. | 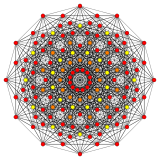 . Исправленный 2 21. . Исправленный 2 21. | |
| ортогональные проекции в E 6Плоскость Кокстера | ||
|---|---|---|
В 6-мерной геометрии многогранник 122представляет собой однородный многогранник , построенный из группы E6. Впервые он был опубликован в E. Список полуправильных многогранников Л. Элте за 1912 год, названных V 72 (для 72 вершин).
Его символ Кокстера - 122, описывающую его раздваивающуюся диаграмму Кокстера-Дынкина с одним кольцом на конце последовательности с 1 узлом. Имеется два исправления 1 22, построенных путем позиционирования точек на элементах 1 22. Выпрямленный 1 22состоит из точек на средних краях 122. двунаправленный 1 22построен из точек в центрах граней треугольника 122.
. Эти многогранники принадлежат к семейству из 39 выпуклых однородных многогранников в 6-мерном, состоящих из однородный многогранник фасеты и фигуры вершин, определенные всеми перестановками колец на этой диаграмме Кокстера-Дынкина : ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
| 122многогранник | |
|---|---|
| Тип | Однородный 6-многогранник |
| Семейный | 1k2многогранник |
| Шлеф символ li | {3,3} |
| символ Кокстера | 122 |
| диаграмма Кокстера-Дынкина | |
| 5- лица | 54:. 27 121 |
| 4-гранный | 702:. 270 111 |
| Ячейки | 2160:. 1080 110 |
| Грани | 2160 {3} |
| Ребра | 720 |
| Вершины | 72 |
| Вершинная фигура | Двунаправленная 5-симплексная :. 022 |
| многоугольник Петри | Додекагон |
| группа Кокстера | E6, [[3,3]], порядок 103680 |
| Свойства | выпуклый, изотопический |
Многогранник 1_22 содержит 72 вершины и 54 5-полукубических фасетов. Он имеет двунаправленную 5-симплексную фигуру вершин. Его 72 вершины представляют собой корневые векторы простой группы Ли E6.
| E6. [12] | D5. [8] | D4 / A2. [6] | |
|---|---|---|---|
 . (1,2) . (1,2) | 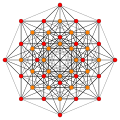 . (1, 3) . (1, 3) |  . (1,9,12) . (1,9,12) | |
| B6. [12/2] | A5. [6] | A4. [[5]] = [10] | A3 / D3. [4] |
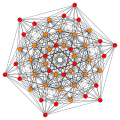 . (1,2) . (1,2) | 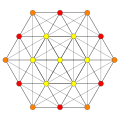 . (2,3,6) . (2,3,6) | 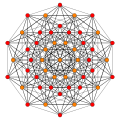 . (1,2) . (1,2) | 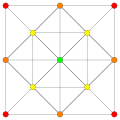 . (1,6,8,12) . (1,6,8,12) |
Он создается с помощью конструкции Wythoff на наборе из 6 гиперплоскостей зеркал в 6-мерном пространстве.
Информация о фасетах может быть извлечена из его диаграммы Кокстера-Дынкина, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Удаление узла на любой из двух ветвей длины оставляет 5-полукуб, 1 31, ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Фигурка вершины определяется удалением окруженного узла и вызовом соседнего узла. Это делает двунаправленный 5-симплексный, 0 22, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
. Рассматриваемый в матрице конфигурации, количество элементов может быть получено путем удаления зеркала и соотношений группы Кокстера приказы.
| E6 | k-face | fk | f0 | f1 | f2 | f3 | f4 | f5 | k-figure | notes | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A5 | () | f0 | 72 | 20 | 90 | 60 | 60 | 15 | 15 | 30 | 6 | 6 | r {3,3,3} | E6/A5= 72 * 6! / 6! = 72 | |
| A2A2A1 | {} | f1 | 2 | 720 | 9 | 9 | 9 | 3 | 3 | 9 | 3 | 3 | {3} x {3} | E6/A2A2A1= 72 * 6! / 3! / 3! / 2 = 720 | |
| A2A1A1 | {3} | f2 | 3 | 3 | 2160 | 2 | 2 | 1 | 1 | 4 | 2 | 2 | s {2,4} | E6/A2A1A1= 72 * 6! / 3! / 2/2 = 2160 | |
| A3A1 | {3,3} | f3 | 4 | 6 | 4 | 1080 | * | 1 | 0 | 2 | 2 | 1 | {} v () | E6/A3A1= 72 * 6! / 4! / 2 = 1080 | |
| 4 | 6 | 4 | * | 1080 | 0 | 1 | 2 | 1 | 2 | ||||||
| A4A1 | {3,3,3} | f4 | 5 | 10 | 10 | 5 | 0 | 216 | * | * | 2 | 0 | {} | E6/A4A1= 72 * 6! / 5! / 2 = 216 | |
| 5 | 10 | 10 | 0 | 5 | * | 216 | * | 0 | 2 | ||||||
| D4 | ч {4,3,3} | 8 | 24 | 32 | 8 | 8 | * | * | 270 | 1 | 1 | E6/D4= 72 * 6! / 8/4! = 270 | |||
| D5 | ч {4,3,3,3} | f5 | 16 | 80 | 160 | 80 | 40 | 16 | 0 | 10 | 27 | * | () | E6/D5= 72 * 6! / 16/5! = 27 | |
| 16 | 80 | 160 | 40 | 80 | 0 | 16 | 10 | * | 27 | ||||||
 Ортографическая проекция на плоскость Кокстера Aut (E6) с 18-угольной симметрией для сложного многогранника, 3 {3} 3 {4} 2. Он имеет 72 вершины, 216 3-ребер и 54 3 {3} 3 грани.
Ортографическая проекция на плоскость Кокстера Aut (E6) с 18-угольной симметрией для сложного многогранника, 3 {3} 3 {4} 2. Он имеет 72 вершины, 216 3-ребер и 54 3 {3} 3 грани. правильный комплексный многогранник 3{3} 3 {4} 2, ![]()
![]()
![]()
![]()
![]() , в
, в 
![]()
![]()
![]()
![]()
![]() , как выпрямление многогранника Гессе,
, как выпрямление многогранника Гессе, ![]()
![]()
![]()
![]()
![]() .
.
Наряду с полуправильным многогранником 221 он также является одним из семейство 39 выпуклых однородных многогранников в 6-мерном пространстве, состоящих из граней однородного многогранника и вершинных фигур, определенных всеми перестановками колец в этом Coxeter -Диаграмма Дынкина : ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
| 1k2цифры в n измерениях | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Пространство | Конечное | Евклидово | Гиперболическое | ||||||||
| n | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| Кокстера. группа | E3=A2A1 | E4=A4 | E5=D5 | E6 | E7 | E8 | E9=  = E 8 = E 8 | E10=  = E 8 = E 8 | |||
| Диаграмма Кокстера. | |||||||||||
| Симметрия. (порядок) | [3] | [3] | [ 3] | [[3]] | [3] | [3] | [3] | [3] | |||
| Заказ | 12 | 120 | 1,920 | 103,680 | 2,903,040 | 696,729,600 | ∞ | ||||
| График |  |  |  |  |  |  | - | - | |||
| Имя | 1−1,2 | 102 | 112 | 122 | 132 | 142 | 152 | 162 | |||
122связано с 24 ячейки геометрическим складыванием E6 → F4 из диаграмм Кокстера-Дынкина, E6 соответствует 122в 6 измерениях, F4 - к 24 ячейкам в 4 измерениях. Это можно увидеть в проекциях плоскости Кокстера. 24 вершины 24-ячеечной проекции проецируются в те же два кольца, что и в плоскостях Кокстера 1 22.
| E6 / F4 | |
|---|---|
 . 122 . 122 |  . 24-ячеечная . 24-ячеечная |
| D4 / B4-плоскость Кокстера | |
 . 122 . 122 |  . 24-ячейка . 24-ячейка |
Этот многогранник является вершинной фигурой для однородной мозаики 6-мерного пространства, 222, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
| Выпрямленный 1 22 | |
|---|---|
| Тип | Равномерный 6-многогранник |
| символ Шлефли | 2r {3,3,3}. r {3,3} |
| символ Кокстера | 0221 |
| Диаграмма Кокстера-Дынкина | |
| 5- лица | 126 |
| 4- лица | 1566 |
| Ячейки | 6480 |
| Лица | 6480 |
| Ребра | 6480 |
| Вершины | 720 |
| Вершинная фигура | призма 3-3 с двойной призмой |
| многоугольник Петри | Додекагон |
| Группа Кокстера | E6, [[3,3]], порядок 103680 |
| Свойства | выпуклый |
Многогранник выпрямленный 1 22(также называемый 0 221 ) может мозаизировать 6-мерное пространство как ячейка Вороного соты E6 * решетки (двойственной решетке E6).
Вершины окрашены по их множественности в этой проекции в прогрессивном порядке: красный, оранжевый, желтый.
| E6. [12] | D5. [8] | D4 / A2. [6] | B6. [12/2] |
|---|---|---|---|
 |  | 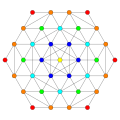 | 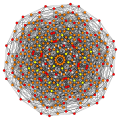 |
| A5. [6] | A4. [5] | A3 / D3. [4] | |
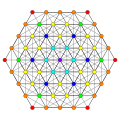 |  | 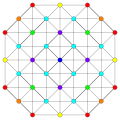 |
Его конструкция основана на группе E6, и информация может быть извлечена из закольцованной диаграммы Кокстера-Дынкина, представляющей этот многогранник: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Удаление кольца на короткой ветке оставляет двунаправленный 5-симплекс, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Удаление кольца на двух листах ветви двунаправленный 5-ортоплекс в его альтернативной форме: t2(211), ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
фигура вершины определяется путем удаления окруженного узла и звонка в соседнее кольцо. Это делает призму 3-3 дуопризмы, {3} × {3} × {}, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
. При отображении в матрице конфигурации количество элементов может быть получено путем удаления зеркала и соотношения группы Кокстера заказов.
| E6 | k-face | fk | f0 | f1 | f2 | f3 | f4 | f5 | k-figure | примечания | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A2A2A1 | () | f0 | 720 | 18 | 18 | 18 | 9 | 6 | 18 | 9 | 6 | 9 | 6 | 3 | 6 | 9 | 3 | 2 | 3 | 3 | {3} x {3} x {} | E6/A2A2A1= 72 * 6! / 3! / 3! / 2 = 720 | |
| A1A1A1 | {} | f1 | 2 | 6480 | 2 | 2 | 1 | 1 | 4 | 2 | 1 | 2 | 2 | 1 | 2 | 4 | 1 | 1 | 2 | 2 | {} v {} v () | E6/A1A1A1= 72 * 6! / 2/2/2 = 6480 | |
| A2A1 | {3} | f2 | 3 | 3 | 4320 | * | * | 1 | 2 | 1 | 0 | 0 | 2 | 1 | 1 | 2 | 0 | 1 | 2 | 1 | Клиновидная область | E6/A2A1= 72 * 6! / 3! / 2 = 4320 | |
| 3 | 3 | * | 4320 | * | 0 | 2 | 0 | 1 | 1 | 1 | 0 | 2 | 2 | 1 | 1 | 1 | 2 | ||||||
| A2A1A1 | 3 | 3 | * | * | 2160 | 0 | 0 | 2 | 0 | 2 | 0 | 1 | 0 | 4 | 1 | 0 | 2 | 2 | {} ∨ {} | E6/A2A1A1= 72 * 6! / 3! / 2/2 = 2160 | |||
| A2A1 | {3,3} | f3 | 4 | 6 | 4 | 0 | 0 | 1080 | * | * | * | * | 2 | 1 | 0 | 0 | 0 | 1 | 2 | 0 | {} v () | E6/A2A1= 72 * 6! / 3! / 2 = 1080 | |
| A3 | r {3,3} | 6 | 12 | 4 | 4 | 0 | * | 2160 | * | * | * | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | {3} | E6/A3= 72 * 6! / 4! = 2160 | ||
| A3A1 | 6 | 12 | 4 | 0 | 4 | * | * | 1080 | * | * | 0 | 1 | 0 | 2 | 0 | 0 | 2 | 1 | {} v () | E6/A3A1= 72 * 6! / 4! / 2 = 1080 | |||
| {3,3} | 4 | 6 | 0 | 4 | 0 | * | * | * | 1080 | * | 0 | 0 | 2 | 0 | 1 | 1 | 0 | 2 | |||||
| r {3,3} | 6 | 12 | 0 | 4 | 4 | * | * | * | * | 1080 | 0 | 0 | 0 | 2 | 1 | 0 | 1 | 2 | |||||
| A4 | r {3,3,3} | f4 | 10 | 30 | 20 | 10 | 0 | 5 | 5 | 0 | 0 | 0 | 432 | * | * | * | * | 1 | 1 | 0 | {} | E6/A4= 72 * 6! / 5! = 432 | |
| A4A1 | 10 | 30 | 20 | 0 | 10 | 5 | 0 | 5 | 0 | 0 | * | 216 | * | * | * | 0 | 2 | 0 | E6/A4A1= 72 * 6! / 5! / 2 = 216 | ||||
| A4 | 10 | 30 | 10 | 20 | 0 | 0 | 5 | 0 | 5 | 0 | * | * | 432 | * | * | 1 | 0 | 1 | E6/A4= 72 * 6! / 5! = 432 | ||||
| D4 | ч {4,3,3} | 24 | 96 | 32 | 32 | 32 | 0 | 8 | 8 | 0 | 8 | * | * | * | 270 | * | 0 | 1 | 1 | E6/D4= 72 * 6! / 8/4! = 270 | |||
| A4A1 | r {3,3,3} | 10 | 30 | 0 | 20 | 10 | 0 | 0 | 0 | 5 | 5 | * | * | * | * | 216 | 0 | 0 | 2 | E6/A4A1= 72 * 6! / 5! / 2 = 216 | |||
| A5 | 2r {3,3,3,3} | f5 | 20 | 90 | 60 | 60 | 0 | 15 | 30 | 0 | 15 | 0 | 6 | 0 | 6 | 0 | 0 | 72 | * | * | () | E6/A5= 72 * 6! / 6! = 72 | |
| D5 | rh{4,3,3,3} | 80 | 480 | 320 | 160 | 160 | 80 | 80 | 80 | 0 | 40 | 16 | 16 | 0 | 10 | 0 | * | 27 | * | E6/D5= 72 * 6! / 16 / 5! = 27 | |||
| 80 | 480 | 160 | 320 | 160 | 0 | 80 | 40 | 80 | 80 | 0 | 0 | 16 | 10 | 16 | * | * | 27 | ||||||
| Усеченный 1 22 | |
|---|---|
| Тип | Однородный 6-многогранник |
| символ Шлефли | t {3,3} |
| символ Кокстера | t (1 22) |
| диаграмма Кокстера-Дынкина | |
| 5- лица | 72 + 27 +27 |
| 4- лица | 32 + 216 + 432 + 270 + 216 |
| Ячейки | 1080 + 2160 + 1080 + 1080 + 1080 |
| Лица | 4320 + 4320 + 2160 |
| Ребра | 6480 + 720 |
| Вершины | 1440 |
| Фигура вершины | () v {3} x {3} |
| Многоугольник Петри | Додекагон |
| Группа Кокстера | E6, [[3,3]], порядок 103680 |
| Свойства | выпуклый |
Его построение основано на группе E6, и информация может быть извлечена из кольцевой диаграммы Кокстера-Дынкина, представляющей этот многогранник: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Вершины окрашены в соответствии с их множеством в этой проекции в последовательном порядке: красный, оранжевый, желтый.
| E6. [12] | D5. [8] | D4 / A2. [6] | B6. [12/2] |
|---|---|---|---|
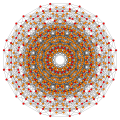 |  | 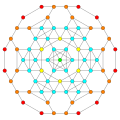 |  |
| A5. [6] | A4. [5] | A3 / D3. [4] | |
 |  |  |
| Двунаправленный 1 22 многогранник | |
|---|---|
| Тип | Равномерный 6-многогранник |
| символ Шлефли | 2r {3,3} |
| символ Кокстера | 2r (1 22) |
| диаграмма Кокстера-Дынкина | |
| 5- лица | 126 |
| 4- лица | 2286 |
| Ячейки | 10800 |
| Лица | 19440 |
| Края | 12960 |
| Вершины | 2160 |
| Вершинная фигура | |
| Группа Кокстера | E6, [[3,3]], порядок 103680 |
| Свойства | выпуклый |
Вершины окрашены в соответствии с их множеством в этой проекции в прогрессивном порядке: красный, оранжевый, желтый.
| E6. [12] | D5. [8] | D4 / A2. [6] | B6. [12/2] |
|---|---|---|---|
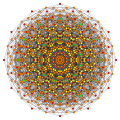 |  | 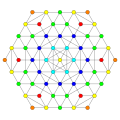 | 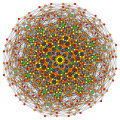 |
| A5. [6] | A4. [5] | A3 / D3. [4] | |
 | 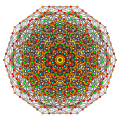 | 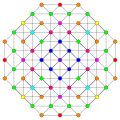 |
| Триректифицированный 1 22 многогранник | |
|---|---|
| Тип | Равномерный 6-многогранник |
| символ Шлефли | 3r {3,3} |
| символ Кокстера | 3r (1 22) |
| диаграмма Кокстера-Дынкина | |
| 5-грань | 558 |
| 4 лица | 4608 |
| Ячейки | 8640 |
| Лица | 6480 |
| Края | 2160 |
| Вершины | 270 |
| Вершина | |
| группа Кокстера | E6, [[3,3]], порядок 103680 |
| Свойства | выпуклый |
.
| ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | ||||||||
| Треугольник | Квадрат | p-угольник | Шестиугольник | Пентагон | ||||||||
| Тетраэдр | Октаэдр • Куб | Демикуб | Додекаэдр • Икосаэдр | |||||||||
| 5-элементный | 16-элементный • Тессеракт | Димитессеракт | 24-элементный | 120-элементный • 600-элементный | ||||||||
| 5-симплекс | 5-ортоплекс • 5-куб | 5-полукуб | ||||||||||
| 6-симплекс | 6-ортоплекс • 6-куб | 6-полукуб | 122 • 221 | |||||||||
| 7-симплекс | 7-ортоплекс • 7-куб | 7-полукуб | 132 • 231 • 321 | |||||||||
| 8-симплекс | 8-ортоплекс • 8-куб | 8-полукуб | 142 • 241 • 421 | |||||||||
| 9-симплекс | 9-ортоплекс • 9-куб | 9-полукуб | ||||||||||
| 10-симплекс | 10 -ортоплекс • 10-куб | 10-полукуб | ||||||||||
| n-симплекс | n-ортоплекс • n- куб | n-полукуб | 1k2 • 2k1 • k21 | n-пятиугольный многогранник | ||||||||
| Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений | ||||||||||||