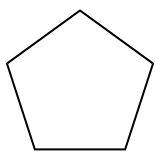
 . Правильный пятиугольник - это многоугольник, двойной -мерный многогранник с 5 ребрами, представленный символом Шлефли {5}. . Правильный пятиугольник - это многоугольник, двойной -мерный многогранник с 5 ребрами, представленный символом Шлефли {5}. | 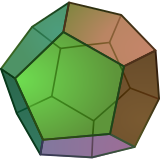 . Правильный додекаэдр - это многогранник, трехмерный многогранник с 12 пятиугольными гранями, представленный символом Шлефли {5,3}. . Правильный додекаэдр - это многогранник, трехмерный многогранник с 12 пятиугольными гранями, представленный символом Шлефли {5,3}. |
 . Правильный 120-элементный - это 4-многогранник, четырехмерный многогранник со 120 додекаэдрическими ячейками, представленный символом Шлефли {5, 3,3}. (здесь как диаграмма Шлегеля ) . Правильный 120-элементный - это 4-многогранник, четырехмерный многогранник со 120 додекаэдрическими ячейками, представленный символом Шлефли {5, 3,3}. (здесь как диаграмма Шлегеля ) |  . Обычная кубическая сотовая структура - это тесселяция, бесконечный трехмерный многогранник, представленный символом Шлефли {4,3,4}. . Обычная кубическая сотовая структура - это тесселяция, бесконечный трехмерный многогранник, представленный символом Шлефли {4,3,4}. |
 . 256 вершин и 1024 ребра 8-куба могут быть показаны в этой ортогональной системе (многоугольник Петри ) . 256 вершин и 1024 ребра 8-куба могут быть показаны в этой ортогональной системе (многоугольник Петри ) | |
В математике, a регулярный многогранник - это многогранник, группа симметрии которого действует транзитивно на его флаги, тем самым придавая ему высшую степень симметрии. (для всех 0 ≤ j ≤ n, где n - размерность многогранника) - ячейки, грани и т. Д. - также транзитивны на симметриях многогранника и являются правильными многогранниками размерности ≤ n.
Правильные многогранники являются общим аналогом любого числа измерений правильных многоугольников (например, квадрат или правильный пятиугольник) и правильные многогранники (на пример, куб ). Сильная симметрия Гулярные многогранники придают им эстетическое качество, которое интересует как нематематиков, так и математиков.
Классически правильный многогранник в измерениях может быть определен как имеющий правильные фасеты [(n - 1) -грани] и правильные фигуры вершин. Этих двух условий достаточно, чтобы все грани и все вершины одинаковы. Однако обратите внимание, что это определение не работает для абстрактных многогранников.
Регулярный многогранник может быть символом Шлефли формы {a, b, c,...., y, z}, с правильными фасетами как {a, b, c,..., y} и правильными фигурами вершин как {b, c,..., y, z}.
Регулярные многогранники классифицируются в первую очередь по их размерности.
Их можно также классифицировать согласно симметрии. Например, куб и правильный октаэдр обладают одинаковой симметрией, как и правильный додекаэдр и икосаэдр. Действительно, группы симметрии иногда называют в честь правильных многогранников, например тетраэдрической и икосаэдрической симметрии.
Три специальных класса регулярных многогранников существуют в каждом измерении:
В двух измерениях, существует бесконечно много правильных многоугольников. В трехмерном и четырехмерном измерении, кроме этих трех, есть еще несколько правильных многогранников и 4-многогранников. В пяти измерений и выше они единственные. См. Также список правильных многогранников.
Идея многогранника иногда обобщается, чтобы включить связанные виды геометрических объектов. Некоторые из них имеют регулярные примеры, как обсуждается в разделе об исторических открытиях ниже.
Краткое символическое представление правильных многогранников было разработано Людвигом Шлефли в 19 веке и слегка измененная форма стала стандартом. Обозначения лучше всего пояснять, добавляя по одному измерению за раз.
, двойственная правильному многограннику также является правильным многогранником. Символ Шлефли для двойного многогранника - это просто исходный символ, записанный в обратном направлении: {3, 3} самодвойственен, {3, 4} двойственен к {4, 3}, {4, 3, 3} к {3, 3, 4 } и так далее.
Вершинная фигура правильного многогранника является двойной граньюственного двойного многогранника. Например, фигура вершины {3, 3, 4} - это {3, 4}, двойная к которой - {4, 3} - ячейка из {4, 3, 3}.
Мера мера и перекрестные многогранники в любом измерении двойственны друг другу.
Если символ Шлефли палиндромный, т.е. читается одинаково вперед и назад, то многогранник самодвойственный. Самодвойственные регулярные многогранники:
 |  |  |  |
| Сегмент линии | Треугольник | Тетраэдр | Пентахорон |
 |  |  |
Начните с точки A. Установите точку B на расстоянии r от нее и соедините, чтобы сформировать сегмент линии. Отметьте точку C на втором, ортогональном измерении на расстоянии r от обоих, и соедините с A и B, чтобы сформировать равносторонний треугольник. Отметьте точку D в третьем ортогональном измерении на расстоянии r от всех трех и соедините, чтобы сформировать правильный тетраэдр. И так далее для более высоких измерений.
Это обычные симплексы или симплексы . Их имена в порядке размерности:
 |  |  |
| Квадрат | Куб | Тессеракт |
 |  |  |
Начните с точки A. Продлите линию до точки B на расстоянии r и соедините, чтобы сформировать сегмент линии. Вытяните вторую линию длиной r, ортогональную AB, от B до C, а также от A до D, чтобы сформировать квадрат ABCD. Вытяните каждого линии длины r соответственно от угла, ортогональные как AB, так и BC (то есть вверх). Отметьте новые точки E, F, G, H, чтобы сформировать куб ABCDEFGH. И так далее для более высоких измерений.
Это многогранники с мерой или гиперкубы . Их имена в порядке размерности:
 |  |  |
| Квадрат | Октаэдр | 16-элементный |
 |  |  |
Начните с точки O. Продлите линию в противоположных направлениях до точек A и B на расстоянии r от O и 2r друг от друга. Нарисуйте линию COD длиной 2r с центром в точке O и ортогональной AB. Соедините концы, чтобы сформировать квадрат ACBD. Нарисуйте линию EOF одинаковой длины с центром в точке «O», ортогональную AB и CD (то есть вверх и вниз). Соедините концы с квадратом, чтобы сформировать правильный октаэдр. И так далее для более высоких измерений.
Это кросс-политопы или ортоплексы . Их имена в порядке размерности:
Самое раннее из сохранившихся математических трактовок правильных многоугольников и многогранников пришло к нам от древнегреческих математиков. Им были известны пять Платоновых тел. Пифагор знал по крайней мере о трех из них, а Феэтет (ок. 417 г. до н.э. - 369 г. до н.э.) описал все пять. Позже Евклид написал систематическое исследование математики, опубликовав его под названием Элементы, в котором была построена логическая теория геометрии и теория чисел. Его работа завершилась математическим описанием пяти Платоновых тел.
Наше понимание оставлено неизменным в течение многих столетий после Евклида. Дальнейшая история правильных многогранников может быть охарактеризована расширенным расширением основной концепции, позволяющей рассматривать все больше и больше объектов среди их числа. Томас Брэдвардин (Брадвардинус) был первым, кто сделал серьезное исследование звездных многоугольников. Различные звездные многогранники появляются в искусстве эпохи Возрождения, но только Иоганн Кеплер изучил малый звездчатый додекаэдр и большой звездчатый додекаэдр в 1619 году, когда он осознал эти два были регулярными. Луи Пуансо открыл большой додекаэдр и большой икосаэдр в 1809 году, а Огюстен Коши доказал полный список в 1812 году. Эти многогранники известны вместе многогранники Кеплера-Пуансо.
| многогранники Кеплера-Пуансо | |||
 |  |  |  |
| малые звездчатые. додекаэдры | большие звездчатые. додекаэдры | большие додекаэдры | большие икосаэдры |
 Трехмерная проекция вращающегося тессеракта. Этот тессеракт изначально ориентирован так, чтобы все ребра были параллельны одной из четырех осей координатного пространства. Вращение происходит в плоскости xw.
Трехмерная проекция вращающегося тессеракта. Этот тессеракт изначально ориентирован так, чтобы все ребра были параллельны одной из четырех осей координатного пространства. Вращение происходит в плоскости xw. Только в 19 веке швейцарский математик Людвиг Шлефли исследовал и охарактеризовал правильные многогранники в более высоких измеренийх. Впервые его работы были полностью опубликованы в Шлефли (1901), шесть лет спустя после смерти, хотя некоторые из них были опубликованы в Шлефли (1855) и Шлефли (1858). Между 1880 и 1900 годами результаты Шлефли были независимо открыты, по крайней мере, девятью другими математиками - см. Coxeter (1948, стр. 143–144) harvtxt error: no target: CITEREFCoxeter1948 (help ) Больше подробностей. Шлефли назвал такую фигуру «полисхема» (на английском языке «полисхема» или «полисхема»). Термин «многогранник» был введен Рейнхольдом Хоппе, одним из открывателей Шлефли, в 1882 году впервые использован на английском языке Алисией Буль Стотт около двадцати лет спустя. Термин «многогранники» также использовался в более ранней литературе (Hilbert, 1952).
Coxeter (1948) ошибка harvtxt: нет цели: CITEREFCoxeter1948 (help ), вероятно, наиболее полным печатным описанием результатов Шлефли и аналогичных результатов на сегодняшний день. Шлефли показал, что существует шесть правильных выпуклых многогранников в четырех измерениях. Пять из них можно рассматривать как аналог Платоновых тел: 4-симплекс (или пентахорон) до тетраэдра, гиперкуб (или tesseract ) в куб, 4-ортоплекс (или гексадекахорон, или 16-элементный ) в октаэдр, 120-элементный в додекаэдр и 600-элементный в икосаэдр. Шестой, 24-элементный, можно рассматривать как переходную форму между гиперкубом и 16-элементным, аналогично, как кубооктаэдр и ромбический додекаэдр - переходные формы между кубом и октаэдром.
В пяти и более измерениях есть ровно три правильных многогранника, которые соответствуют тетраэдру, кубу и октаэдру: это правильные симплексы, многогранники измерения и перекрестные многогранники. Их описания можно найти в в списке правильных многогранников. Также интересны звездные правильные 4-многогранники, частично открытые Шлефли.
К концу XIX века математики, такие как Артур Кейли и Людвиг Шлефли, разработали теорию регулярных многогранников в четырех и более измерениях, таких как тессеракт и 24-элементный.
Последние трудно (хотя и возможно) визуализировать, но они все же сохраняют эстетически приятную симметрию своих низкоразмерных собратьев. Тессеракт содержит 8 кубических ячеек. Он состоит из двух кубов в параллельныхгиперплоскостях с вершинами, перекрестно соединенными таким образом, что 8 поперечных реберны по длине и ортогональны 12 + 12 ребрам, расположенным на каждом кубе. Соответствующие грани двух кубов соединяются, образуя оставшиеся 6 кубических граней тессеракта . 24-элементный может быть получен из тессеракта путем соединения 8 вершин каждой из его кубических граней с дополнительной вершиной, чтобы сформировать четырехмерный аналог пирамиды. Обе фигуры, а также другие четырехмерные фигуры могут быть непосредственно визуализированы и изображены с помощью четырехмерных стереографов.
Еще труднее представить себе более современные абстрактные правильные многогранники, такие как 57-элементный или 11-элементный. Однако с математической точки зрения эти объекты имеют те же эстетические качества, что и их более знакомые двух- и трехмерные точки зрения.
В начале 20 века определение правильного многогранника было следующим.
Это «рекурсивное» определение. Он определяет правильность фигур более высоких размеров относительно правильных фигур более низкого измерения. Существует эквивалентное (нерекурсивное) определение, в котором говорится, что многогранник является регулярным, если он имеет достаточную степень симметрии.
Так, например, куб является правильным, потому что если мы выберем вершину куба, которое одно из трех ребер, на оно находится, одно из двух граней, ребро, тогда эта тройка, или flag, (вершина, ребро, грань) может быть отображен на любой другой такой флаг с помощью подходящей симметрии куба. Таким образом, мы можем очень кратко определить правильный многогранник:
В 20-м веке были сделаны некоторые важные изменения. Группы симмет< классических регулярных многогранников были обобщены в то, что теперь называется группой Кокстера. Группы Кокстера также включают группы симметрии регулярных мозаик пространства или плоскости. Например, симметрии бесконечной шахматной доски будет группа Кокстера [4,4].
В первой половине XX века Кокстер и Петри открыли три бесконечные структуры {4, 6}, {6, 4} и {6, 6}. Они назвали их правильными косыми многогранниками, потому что они, казалось, удовлетворяли определению правильного многогранника - все вершины, ребра и грани одинаковы, все углы одинаковы, и фигура не имеет свободных ребер. В настоящее время их называют бесконечными многогранниками или апейроэдрами. Правильные мозаики плоскости {4, 4}, {3, 6} и {6, 3} также можно рассматривать как бесконечные многогранники.
В 1960-е годы Бранко Грюнбаум призвал геометрическое сообщество рассмотреть более абстрактные типы правильных многогранников, которые он назвал полистроматами. Он разработал теорию полистромат, показав примеры новых объектов, которые он назвал регулярными апейротопами, то есть правильными многогранниками с бесконечно многогранностью. Простым примером перекоса апейрогона может быть зигзаг. Кажется, он удовлетворяет определению правильного многоугольника - все ребра одинаковой длины, все углы одинаковы, и у фигуры нет свободных концов (потому что они никогда не достижимы). Что еще более важно, возможно, существуют симметрии зигзага, которые могут отображать любую пару вершины и присоединенного ребра к любой другой. С тех пор продолжали открываться другие обычные апейрогоны и высшие апейротопы.
A комплексное число имеет действительную часть, с которой мы все знакомы, и мнимую часть, которая кратна квадратному корню из минус единицы. Комплексное гильбертово пространство имеет координаты x, y, z и т. Д. В виде комплексных чисел. Это фактически удваивает количество измерений. Многогранник, построенный в таком унитарном пространстве, называется сложным многогранником.
 Hemicube получается из куба путем уравнивания противоположных вершин, ребер и граней. У него 4 вершины, 6 ребер и 3 грани.
Hemicube получается из куба путем уравнивания противоположных вершин, ребер и граней. У него 4 вершины, 6 ребер и 3 грани. Грюнбаум также обнаружил 11-элементный,