 Комплексное число может быть визуально представлено в виде числа пары (a, б) образующие вектор на диаграмме, называемую диаграмму Аргана, представляющую комплексную плоскость. «Re» - действительная ось, «Im» - мнимая ось, и i удовлетворяет i = -1.
Комплексное число может быть визуально представлено в виде числа пары (a, б) образующие вектор на диаграмме, называемую диаграмму Аргана, представляющую комплексную плоскость. «Re» - действительная ось, «Im» - мнимая ось, и i удовлетворяет i = -1. A комплексное число - это число, которое может быть выражено в форме a + bi, где a и b являются действительными числами, а i представляет мнимую единицу, удовлетворяющую уравнение i = -1. Никакое действительное число не удовлетворяет этому уравнению, i называется мнимым числом. Для комплексного числа a + bi, a называется действительной частью, а b называется мнимой частью . Набор комплексных чисел обозначается символом 
Комплексные числа решать некоторые уравнения, не имеющие решений в действительных числах. Например, уравнение

не имеет реального решения, поскольку квадратное действительное число не может быть отрицательным. Однако комплексные числа позволяют решить эту проблему. Идея состоит в том, чтобы расширить число действующие с помощью неопределенного i (иногда называемого мнимой единицей), взятого для удовлетворения отношений i = −1, чтобы решения подобных, подобных предыдущему может быть найден. В этом случае решения являются −1 + 3i и −1 - 3i, что можно проверить, используя тот факт, что i = −1:


Согласно основной теореме алгебры, все многочлены уравнения с действующими или комплексными коэффициентами в одной категории имеют решение в комплексных числах. Напротив, некоторые полиномиальные уравнения с действующими коэффициентами не имеют решения в действительных числах. Итальянскому математику 16 Джероламо Кардано приписывают введение комплексных чисел - в его попытках найти решения кубических уравнений.
Формально комплексную систему счисления можно определить алгебраическое расширение обычных действительных чисел мнимым числом я. Это означает, что комплексные числа можно складывать, вычитать и умножать как полиномы от i по правилам i = −1. Кроме того, комплексные числа также можно разделить на ненулевые комплексные числа. В целом, комплексная система счисления представляет собой поле .
Геометрические комплексные числа расширяют понятие однойерной числовой линии до двумерной комплексная плоскость с использованием горизонтальной оси для действительной части и вертикальной оси для мнимой части. Комплексное число a + bi можно отождествить с точкой (a, b) на комплексной плоскости. Комплексное число, действительная часть которого равна нулю, называется чисто мнимым, и точки для этих чисел лежат на вертикальной оси комплексной плоскости. Точно так же комплексное число, мнимая часть которого равна нулю, можно рассматривать как действительное число, точка которого лежит на горизонтальной оси комплексной плоскости. Комплексные числа также могут быть представлены в полярной форме, которая связывает комплексное число с его величиной от начала координат (величиной) и определенным углом, известным как аргумент комплексного числа.
Геометрическая идентификация комплексных чисел с комплексной плоскостью, которая является евклидовой плоскостью (
 Иллюстрация комплексной плоскости. Действительная часть комплексного числа z = x + iy равна x, а его мнимая часть - y.
Иллюстрация комплексной плоскости. Действительная часть комплексного числа z = x + iy равна x, а его мнимая часть - y. Комплексное число - это число в форме a + bi, где a и b - действительные числа, а i - неопределенное, такое что i = −1. Например, 2 + 3i - комплексное число.
Таким образом, комплексное число определяется как многочлен с действующими коэффициентами в единственном неопределенном i, для которого соотношение i + 1 = 0. На основе определения этого комплексного числа можно складывать и умножать, используя сложение и умножение многочленов. Соотношение i + 1 = 0 индуцирует равенства i = 1, i = i, i = −1 и i = −i, которые выполняются для всех целых k; они позволяют уменьшить любой многочлен, полученный в результате сложения и умножения комплексных чисел, до линейного многочлена от i, опять же формы a + bi с действующими коэффициентами a, b.
Действительное число a называется действительной частью комплексного числа a + bi; действительное число b называется его мнимой частью. Подчеркнем, что мнимая часть не включает множитель i; то есть мнимая часть - это b, а не bi.
Формально комплексные числа как кольцо частных кольца полиномов в неопределенном i, идеалом , порожденным полиномом i + 1 (см. ниже).
Действительное число можно рассматривать как комплексное число a + 0i, мнимая часть которого равно 0. Чисто мнимое число bi - это комплексное число 0 + bi, действительная часть которого Как и в случае с многочленами, обычно пишут a для a + 0i и bi для 0 + bi., когда мнимая часть отрицательна, то есть b = - | b | < 0, it is common to write a − |b|i instead of a + (−|b|)i; for example, for b = −4, 3 − 4i can be written instead of 3 + (−4)i.
Временное умножение неопределенного i и действительного числа коммутативно в многочленах с действующими коэффициентами, многочлен a + bi может быть записан как a + ib. Это часто целесообразно для мнимых частей, обозначаемых выражениями, например, когда b - радикал.
Действующая часть комплексного числа z обозначается Re (z) или ℜ (z); мнимая часть комплексного числа z обозначается через Im (z) или ℑ (z).
 и
и 
набор всех комплексных чисел обозначается 

В некоторых дисциплинах, особенно в электромагнетизме и электротехника, j используется вместо i, поскольку i часто используется для представления электрического тока. В этих случаях комплексные числа записываются как a + bj или a + jb.
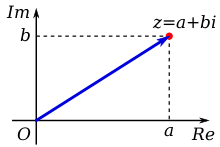 Комплексное число z в виде точки (красный) и его вектор положения (синий)
Комплексное число z в виде точки (красный) и его вектор положения (синий) Таким образом, комплексное число z можно идентифицировать с помощью упорядоченной пары (Re ( z), Im (z)) действительных чисел, которые, в свою очередь, можно интерпретировать как координаты точки в двумерном пространстве. Ближайшее пространство - это евклидова плоскость с подходящими координатами, которая затем называется комплексной плоскостью или диаграммой Аргана, названа в честь Жана-Робера Аргана. Еще одно пространство, которое можно проецировать координаты, - это двумерная поверхность сферы, которая называется сферой Римана.
Определение комплексных чисел, включающих два произвольных реальных значения, подсказывают использование декартовых координаты в комплексной плоскости. Горизонтальная (действительная) ось обычно используется для отображения реальной части с увеличивающимися значениями вправо, а мнимая часть отмечает вертикальную (мнимую) ось с увеличивающимися значениями вверх.
Нанесенное на карту число можно рассматривать либо как скоординированную точку, либо как вектор положения от исходной точки до этой точки. Значения комплексного числа z, следовательно, могут быть выражены в декартовой, прямоугольной или алгебраической форме.
Примечательно, что операции сложения и умножения принимают очень естественный геометрический характер, когда комплексные числа рассматриваются как векторные положения: сложение соответствует сложению векторов, а умножение (см. ниже) соответствует умножению их величин и сложению углов, которые они образуют с действительной осью. С этой точки зрения умножение комплексного числа на i соответствует повороту положения положения против часовой стрелки на четверть оборота (90 ° ) относительно начала координат - факт, который алгебраически может быть выражен следующим образом:

 Аргумент φ и модуль r определяют точку на комплексной плоскости.
Аргумент φ и модуль r определяют точку на комплексной плоскости. Альтернативным исходным положением для координат в комплексной плоскости полярная система координат, которая использует расстояние точки z от точки (O), и угол между положительной действительной осью и отрезком Oz линии против часовой стрелки. Это приводит к полярной форме комплексных чисел.
абсолютное значение (или модуль, или величина) комплексного числа z = x + yi равно

Если z - действительное число (то есть, если y = 0), то r = | х |. То есть абсолютное значение действительного числа равно его абсолютному значению комплексного числа.
Согласно теореме Пифагора, абсолютное значение комплексного числа - это расстояние до начала координат, представляющее комплексное число на комплексной плоскости.
аргумент z (во многих приложенийх называемый «фазой» φ) - это угол радиуса Oz с положительной действительной осью, и он записывается как 


Обычно, как указано выше, выбирается главное значение в интервале (−π, π]. Значения в диапазоне [0, 2π) получаются путем добавления 2π - если значение отрицательное. Значение φ выражается в радиан в этой статье. Он может увеличиваться на любое целое число, кратное 2π, и при давать тот же угол, если смотреть на него, если смотреть на лучи положительной действительной оси и от начала координат через z. Следовательно, функция arg иногда рассматривается как многозначное., но обычно используется произвольный выбор полярно го угла 0.
Значение φ равно результату а tan2 :

Вместе r и φ дают еще один способ представления сложных чисел, полярная форма, так как комбинация модуля и аргумента полностью определяет положение точки на плоскости. Восстановление исходных прямоугольных координат из полярной формы выполняется по формуле называемой тригонометрической формы

Используя формулу Эйлера, это можно записать как

Используя функцию cis, это иногда сокращается до

В формате угла, часто используется в электронике для представления вектор с амплитудой r и фаза φ записывается как

 График цветового круга выражения (z - 1) (z - 2 - i) / z + 2 + 2i
График цветового круга выражения (z - 1) (z - 2 - i) / z + 2 + 2i При визуализации сложные функции, необходимы как комплексный ввод, так и вывод. Визуальное построение графика сложных функций потребует восприятия четырехмерного пространства, что возможно только в проекциях. Из-за этого были разработаны другие способы визуализации сложных функций.
В раскраске домена выходные размеры представлены цветом и яркостью. Каждая точка комплексной плоскости как домена украшена орнаментом, обычно цветом, представляющим аргумент комплексного числа, и яркостью, представляющей. Темные пятна обозначают модули, близкие к нулю, более яркие пятна находятся дальше от начала координат, градация может быть прерывистой, но обязательной монотонной. Цвета часто меняются с шагом π / 3 от 0 до 2π от красного, желтого, зеленого, синего до пурпурного. Эти графики называются графиками цветового круга. Это обеспечивает простой способ визуализации функций без потери информации. На рисунке показаны нули для ± 1, (2 + i) исы при ± √ - 2−2i.
Римановы поверхности - еще один способ визуализировать сложные функции. Римановы поверхности можно рассматривать как деформации комплексной плоскости; в то время как горизонтальные оси соответствующие реальные и мнимые входные данные, единственная вертикальная ось представляет только реальный или мнимый выход. Однако римановы поверхности построены таким образом, что их поворот на 180 градусов показывает воображаемый результат, и наоборот. В отличие от раскраски поверхности, римановы поверхности могут многозначные функции, например 
Решение в радикалах (без тригонометрических функций ) общего кубического уравнения содержит квадратные корни из отрицательных чисел, когда все три корня имеют действительные числа, ситуация, которая не может быть исправленным путем разложения на множители с помощью правильного корня, если кубика несократимая (так называемый casus unducibilis ). Эта загадка привела итальянского математика Джероламо Кардано к мысли о комплексных числах примерно в 1545 году, хотя его понимание было элементомарным.
Работа над проблемой общих многочленов в итоге привела к фундаментальной теореме алгебры, которая показывает, что комплексными числами решение существует для каждого полиномиального уравнения степени один или выше. Таким образом, комплексные числа образуют алгебраически замкнутое поле, где любое полиномиальное уравнение имеет корень.
. Многие математики внесли свой вклад в развитие комплексных чисел. Правила сложения, вычитания, умножения и извлечения корня из комплексных чисел были разработаны итальянским математиком Рафаэлем Бомбелли. Более абстрактный формализм для комплексных чисел был развит ирландским математиком Уильямом Роуэном Гамильтоном, который распространил эту абстракцию на теорию кватернионов.
Самая ранняя мимолетная ссылка на квадратные корни Можно сказать, что из отрицательных чисел встречается в работах греческого математика Героя Александрии в I веке нашей эры, где в своей Stereometrica он считает, очевидно ошибочно, объем невозможной усеченной пирамиды пирамиды, чтобы прийти к термину 

Стимул к изучению комплексные числа как самостоятельная тема впервые возникла в 16 веке, когда алгебраич еские решения для корней кубических и четверных многочленов были открыты итальянскими математиками (см. Никколо Фонтана Тарталья, Джероламо Кардано ). Вскоре стало понятно (но гораздо позже было доказано), что эти формулы, даже если кто-то интересовался только действительными решениями, иногда требовал манипуляции с квадратными корнями из отрицательных чисел. Например, формула Тартальи для кубического уравнения вида 

На первый взгляд это выглядит чепухой. Однако формальные вычисления с комплексными числами показывают, что уравнение z = i имеет решения −i, 


Термин «мнимые» для этих величин был введен Рене Декартом в 1637 году, хотя он изо всех сил старался подчеркнуть их воображаемую природу
[...] иногда только воображаемую, то есть количество, которое можно представить в каждом уравнении, но иногда не существует количества, которое соответствует тому, что мы представляем. ([...] quelquefois seulement imaginaires c'est-à-dire que l'on peut toujours en imaginer autant que j'ai dit en chaque équation, mais qu'il n'y a quelquefois aucune Quantité qui correde à celle qu 'представьте себе.)
Еще одним путаницы было то, что уравнение 


В 18 веке комплексные числа получили более широкое распространение, как было замечено. Например, в 1730 году Абрахам де Муавр заметил, что сложные тождества, связывающие тригонометрические функции целого кратного угла со степенями тригонометрических функций этого угла, могут быть просто перевыражены следующей хорошо известной формулой, которая носит его имя, формула де Муавра :

В 1748 году Леонард Эйлер пошел дальше и получена формула Эйлера из комплексного анализа :

путем формального манипулирования сложными степенными рядами и заметил, что эту формулу можно использовать для сведения любого тригонометрического тождества к гораздо более простым экспоненциальным тождествам.
Идея комплексного числа как точки на комплексной плоскости (выше) была впервые описана Каспаром Весселем в 1799 году, хотя это ожидалось еще раньше. как 1685 в Уоллис Трактат по алгебре.
Мемуары Весселя появились в Трудах Копенгагенской академии, но остались в основном незамеченными. В 1806 году Жан-Робер Арган независимо выпущил брошюру о комплексных числах и предоставил строгое доказательство фундаментальной теоремы алгебры. Карл Фридрих Гаусс ранее опубликовал по существу топологическое доказательство теоремы в 1797 году, но выразил свои сомнения в то время по поводу «истинной метафизики квадратного корня из -1». Лишь в 1831 году он преодолел эти вопросы и опубликовал свой трактат о комплексных числах как точках на плоскости, степени в области современных обозначений и терминологию.
Если раньше кто-то рассматривал этот предмет с ложной точки зрения, то обнаружил таинственную тьму, это в степени степени с неуклюжей терминологией. Если бы кто-то не назвал +1, −1, √ - 1 положительными, отрицательными или воображаемыми (или даже невозможными) единицами, а вместо этого, скажем, прямыми, обратными или боковыми единицами, то вряд ли можно было бы говорить о таком темноте. - Гаусс
В начале 19 века другие математики независимо друг от друга открыли геометрическое представление комплексных чисел: Буэ, Мурей,, Франсэ и его брат, Беллавитис.
Английский математик Г.Х. Харди заметил, что Гаусс был первым математиком, который использовал комплексные числа «действительно уверенным и научным способом», хотя математики, такие как Нильс Хенрик Абель и Карл Густав Якоб Якоби, обязательно были регулярно использовали их до того, как Гаусс опубликовал свой трактат 1831 года.
Огюстен Луи Коши и Бернхард Риман вместе довели фундаментальные идеи комплексного анализа до высокого уровня завершения, начиная с около 1825 года в случае Коши.
Общие термины, используемые в теории, в основном принадлежат основателям. Арган назвал 




Более поздние классические писатели по общей теории Ричард Дедекинд, Отто Гёльдер, Феликс Клейн, Анри Пуанкаре, Герман Шварц, Карл Вейерштрасс и многие другие.
Комплексные числа имеют такое же определение равенства, что и действительные числа; два комплексных числа 



В отличие от действительных чисел, комплексные числа не упорядочиваются естественным образом. В частности, комплексными числами, существующими как существующими на двумерной плоскости, не существует линейного упорядочения комплексных чисел, совместимого со сложением и умножением - комплексные числа не иметь структуру могут упорядоченное поле. Это потому, что любой квадрат в упорядоченном поле не меньше 0, но i = -1.
 Геометрическое представление z и его сопряженного
Геометрическое представление z и его сопряженного  в комплексной плоскости
в комплексной плоскости комплексно сопряженное комплексного числа z = x + yi задается как x - yi. Он обозначается либо 
Геометрически 

, что делает эту операцию инволюцией. Отражение оставляет без изменений действующую часть и действие 
 и
и 
Мнимая часть и аргумент комплексного числа 
 и
и 
Подробнее об аргументе и величине см. раздел Полярная форма.
Произведение комплексного числа 

Это свойство можно использовать для преобразования дроби с комплексным знаменателем в эквивалентную дробь с действительным знаменателем увеличения числителя и знаменателя дроби на конъюгат данного знаменателя. Этот процесс иногда называют «рационализацией » знаменателя (хотя знаменатель в окончательном выражении может быть иррациональным действительным числом), потому что он напоминает метод удаленияней из простых выражений в знаменателе.
Действительная и мнимая части комплексного числа z могут быть извлечены с помощью спряжения:
 и
и 
Более того, комплексное число является действительным тогда и только тогда, когда оно равно собственный сопряженный.
Сопряжение распределяется по основным сложным арифметическим операциям:


Сопряжение также используется в инверсивной геометрии, ветке геометрии, изучающей более общие отражения, чем отражения относительно линии. В сетевом анализе электрических цепей комплексное сопряжение используется для нахождения эквивалентного импеданса, когда ищется теорема о максимальной передаче мощности.
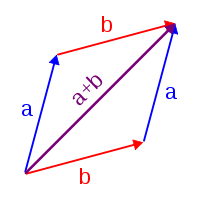 Сложение двух комплексных чисел можно выполнить геометрически, построив параллелограмм.
Сложение двух комплексных чисел можно выполнить геометрически, построив параллелограмм. Два комплексных числа 


Аналогично, вычитание может быть выполнено как

Используя визуализацию комплексных чисел на комплексной плоскости, сложение имеет следующую геометрическую интерпретацию: сумма двух комплексных чисел 








Поскольку действительная часть, мнимая часть и неопределенная 




Используя спряжение, обратное ненулевого комплексное число z = x + yi всегда можно разбить до

, поскольку ненулевое значение означает, что 
Разговор для обозначения деления произвольного комплексного числа 


 Умножение 2 + i (синий треугольник) и 3 + i ( красный треугольник). Красный треугольник поворачивается так, чтобы вершине синего треугольника, и растягиваться на √5, длина гипотенузы синего треугольника.
Умножение 2 + i (синий треугольник) и 3 + i ( красный треугольник). Красный треугольник поворачивается так, чтобы вершине синего треугольника, и растягиваться на √5, длина гипотенузы синего треугольника. Формулы для умножения, деления и в полярной форме возмещения в степени проще, чем соответствующие формулы в декартовых координатах. Даны два комплексных числа z 1 = r 1 (cos φ 1 + i sin φ 1) и z 2 = r 2 (cos φ 2 + i sin φ 2) из-за тригонометрических тождеств


мы можем вывести

Другими словами, абсолютные значения умножаются, аргументы складываются, чтобы получить полярную форму продукта. Например, умножение на i соответствует повороту на четверть против стрелки, что возвращает i = -1. На рисунке справа показано умножение

Действительная и мнимая части 5 + 5i равны, аргумент этого числа равен 45 градусов, или π / 4 (в радиан ). С другой стороны, это также сумма углов в начале красного и синего треугольников: arctan (1/3) и arctan (1/2), соответственно. Таким образом, формула

выполнено. Функция времени arctan может быть аппроксимирована очень эффективно, такие формулы - известные как формулы типа Машина - используются для высокоточных приближений π.
.

Квадратный корень из a + bi (с б ≠ 0) равны 

и

где sgn - это функция signum. Это можно увидеть, возведя в квадрат 


экспоненциальная функция 

с бесконечным числом радиус сходимости.
Значение 1 экспоненциальной функции равно число Эйлера

Если z действительно, значит 

Экспоненциальная функция удовлетворяет функциональному уравнению 
Формула Эйлера утверждает, что для любого действительного числа x

Таким образом, функциональное уравнение подразумевает, что если x и y действительны, то

который представляет собой разложение экспоненциальной функции на ее действительные и мнимые части.
Если x>0 является действительным, а z комплексным, возведение в контексте как

где ln обозначает натуральный логарифм.
Кажется естественным распространить эту формулу на комплексные значения x, но некоторые трудности, связанные с тем, что комплексный логарифм на самом деле не функция, а многозначная функция.
В реальном случае натуральный логарифм может быть определен как , обратный экспоненциальной функции. Чтобы распространить это на комплексную область, можно начать с формулы Эйлера. Это означает, что если комплексное число z записано в полярной форме

, то его комплексный логарифм должен быть

Однако, поскольку косинус и синус являются периодическими функциями, добавление к 




Следовательно, комплексный логарифм должен быть определен как многозначная функция :

В качестве альтернативы, a разрез можно использовать для определения истинной функции. Если z не является отрицательным действительным числом, главное значение комплексного логарифма получается с помощью 
Отсюда следует, что если z такое же, как указано выше, и если t - другое комплексное число, то возведение в степень представляет собой многозначную функцию

 Геометрическое представление из корней 2–6 комплексного числа z в полярной форме re, где r = | z | и φ = arg z. Если z вещественное число, φ = 0 или π. Основные корни показаны черным.
Геометрическое представление из корней 2–6 комплексного числа z в полярной форме re, где r = | z | и φ = arg z. Если z вещественное число, φ = 0 или π. Основные корни показаны черным. Если в предыдущей формуле t - целое число, то синус и косинус не зависит от k. Таким образом, показатель степени n является целым числом, то 

n корней n-й степени комплексного числа z:
![{\ displaystyle z ^ {1 / n} = {\ sqrt [{n}] {r}} \ left (\ cos \ left ({\ frac {\ varphi + 2k \ pi} {n}} \ right) + i \ sin \ left ({\ frac {\ varphi + 2k \ pi} {n}} \ right) \ вправо)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1cc1b3406644f788c1ac1799d6328118ee66516f)
для 0 ≤ k ≤ n - 1. (Здесь ![{\ displaystyle {\ sqrt [{n}] {r}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10eb7386bd8efe4c5b5beafe05848fbd923e1413)
Хотя корень n-й степени положительного действующего числа r выбран как положительное действующее число c, удовлетворяющее с = r, естественное качество отличить один конкретный комплексный корень n-й степени комплексного числа не существует. Следовательно, корень n-й степени является n-значной функцией от z. Это означает, что в отличие от положительных действующих чисел,

так как левая часть состоит из n значений, а правая часть - одно значение.
Набор C комплексных чисел - это поле . Вкратце, это означает, что верны следующие факты: во-первых, любые два комплексных числа можно сложить и умножить, чтобы получить другое комплексное число. Во-вторых, для любого комплексного числа z его аддитивная обратная величина -z также является комплексным числом; и в-третьих, ненулевое комплексное число имеет обратное комплексное число. Более того, эти операции выполняют ряду операций, например, закону коммутативности сложения и умножения любых двух комплексных чисел z 1 и z 2:


Эти два закона и другие требования к полю можно доказать с помощью приведенных выше формул, используя тот факт, что реальный сами числа образуют поле.
В определение от вещественных чисел, C не является упорядоченным полем, то есть невозможно отношение z 1< z2, совместимое с сложение и умножение. Фактически, в любом упорядоченном поле квадратного элемента любого обязательно положителен, поэтому i = −1 исключает возможность упорядочивания на C.
, когда базовое поле для математической темы или конструкции является поле комплексных чисел, название темы обычно изменяется, чтобы отразить этот факт. Например: комплексный анализ, комплексная матрица, комплексный полином и комплексный алгебра Ли.
Для любых комплексных чисел (называемых коэффициентами ) a 0,..., a n уравнение

имеет хотя бы одно комплексное решение z при условии, что хотя бы одно из более высоких коэффициентов a 1,..., a n не равны нулю. Это утверждение фундаментальной теоремы алгебры, Карла Фридриха Гаусса и Жана ле Ронда д'Аламбера. По этой причине C называется алгебраически замкнутым полем. Это свойство не выполняется ни для поля рациональных чисел Q(многочлен x - 2 не имеет рационального корня, поскольку √2 не является рациональным числом), ни для действительных чисел R (многочлен x + a не имеет действительного корня при a>0, поскольку квадрат x положителен для любого действительного числа x).
Существуют доказательства этой теоремы либо аналитическими методами, такими как теорема Лиувилля, либо топологическими, такими как число витков, или доказательство, сочетающее теорию Галуа и тот факт, что любой действительный многочлен нечетной степени имеет хотя бы один действительный корень.
По этой причине теоремы, справедливые для любого алгебраически замкнутого поля, применимы к C . Например, любая непустая комплексная квадратная матрица имеет по крайней мере одно (комплексное) собственное значение.
Поле C имеет следующие три свойства: во-первых, он имеет характеристику 0. Это означает, что 1 + 1 + ⋯ + 1 ≠ 0 для любого количества слагаемых (все они равны одному). Во-вторых, его степень превосходства над Q, простое поле в C, является мощностью континуума. В-третьих, это алгебраически замкнутый (см. Выше). Можно показать, что любое поле, имеющее эти свойства, изоморфно (как поле) C . Например, алгебраическое замыкание элемент Qp также удовлетворяет этим трем свойствам, поэтому эти два поля изоморфны (как поля, но не как топологические поля). Кроме того, C изоморфен полюсной комплексной серии Пюизо. Однако для задания изоморфизма требуется аксиома выбора. Другой следствие этой алгебраической характеристики состоит в том, что C содержит множество собственных подполей, которые изоморфны C.
Предыдущая характеристика C имеет только алгебраические аспекты С . То есть, связи и непрерывности, которые имеют значение в таких свойствах области, как анализ и топология, не рассматриваются.. Следующее описание C как топологического поля (то есть поля, снабженного топологией , которое допускает понятие сходимости) учитывает топологические свойства. C содержит подмножество P ненулевых элементов, удовлетворяющих следующим трем условиям:
Более того, C имеет нетривиальный инволютивный автоморфизм x ↦ x * (а именно комплексное сопряжение), такой, что xx * находится в P для любого ненулевого x в C.
Любое поле F с помощью свойства можно снабдить топологией, взяв число B (x, p) = {y | p - (y - x) (y - x) * ∈ P} как база, где x пробегает поле, а p пробегает P. С этой топологией F как топологическое поле изоморфно C.
Единственными локально компактными топологическими полями являются R и C . Это дает другую характеристику C как топологического поля, поскольку C можно отличить от R, что ненулевые комплексные числа связаны, в то время как ненулевые действительные числа - нет.
Уильям Роуэн Гамильтон представил подход для определения набора C комплексные числа как набор R из упорядоченных пар (a, b) действительных чисел, в которых применяются следующие правила сложения и умножения:

Тогда просто вопрос обозначений, чтобы выразить (a, b) как a + bi.
Хотя эта низкоуровневая конструкция действительно имеет характерные комплексные числа, следующее определение раскрывает алгебраическую природу C подробнее немедленно. Эта основа на понятии полей и многочленов. Поле - это набор, наделенные операциями сложения, вычитания, умножения и деления, которые ведут себя так же, как, например, по рациональным числам. Например, закон распределения

должен работать для любых трех элементов x, y и z. поля. Набор R действительных чисел действительно образует поле. Многочлен p (X) с действительными коэффициентами представляет собой выражение вида

где a 0,..., a n - действительные числа. Обычное сложение и умножение многочленов наделяет набор R [X] всех таких многочленов кольцевой структурой . Это кольцо называется кольцом многочленов над действительными числами.
Набор комплексных чисел определяется как кольцо частных R[X] / (X + 1). Это поле расширения содержит два квадратных корня из -1, а именно (дополнительные классы ) X и -X, соответственно. (Смежные классы) 1 и X образуют основу R [X] / (X + 1) как реальное пространство пространства, что означает, что каждый элемент поля расширения может быть однозначно записанным как линейная комбинация в этих двух элементах. Эквивалентно, элементы расширения могут быть записаны как упорядоченные пары (a, b) действительные числа. Фактор-кольцо - это поле, потому что X + 1 неприводимо над R, поэтому порождаемый им идеал максимален.
Формулы для сложения и умножения в кольце R [X] по модулю отношения X = -1 соответствуют формулам для сложения и умножения комплексных чисел, как упорядоченные пары. Таким образом, два определения поля C являются изоморфными (как поля).
Принимая, что C является алгебраически замкнутым, поскольку это алгебраическое расширение R в этом подходе, C поэтому алгебраическим замыканием из R.
Комплексные числа a + bi могут быть представлены матрицами 2 × 2 , которые имеют следующие формы:

Здесь записи a и b - действительные числа. Сумма и произведение двух таких матриц снова формула и имеют произведение комплексных чисел соответствуют сумме и произведению таких матриц, причем произведение будет:

Геометрическое описание умножения комплексных чисел также может быть выражено в терминах матриц вращения, используя это соответствие между комплексными числами и такими матрицами. Более того, квадрат абсолютного значения комплексного числа, выраженного в виде матрицы, равен определителю этой матрицы:

Сопряжение 
Хотя это представление комплексных чисел с матрицами является наиболее распространенным, многие другие представления возникают из матриц, отличных от 
 Цветовой круг греха (1 / z). Черные части внутри относятся к числам, имеющим большие абсолютные значения.
Цветовой круг греха (1 / z). Черные части внутри относятся к числам, имеющим большие абсолютные значения. Изучение функций комплексной переменной известно как комплексный анализ и имеет огромное практическое применение в прикладной математике, а также в других разделах математики. Часто наиболее естественные доказательства утверждений в реальном анализе или даже теории чисел используют методы комплексного анализа (см. теорему о простых числах для примера). В отличие от реальных функций, которые обычно представлены в виде двумерных графиков, сложные функции имеют четырехмерные графики и могут быть с пользой проиллюстрированы с помощью цветного кодирования трехмерного графика, чтобы предложить четыре размеров, или путем анимации динамического преобразования сложной функции комплексной плоскости.
Понятия сходящихся рядов и непрерывных функций в (реальном) анализе имеют естественные аналоги в комплексном анализе. Говорят, что последовательность комплексных чисел сходится тогда и только тогда, когда ее действительная и мнимая части сходятся. Это эквивалентно (ε, δ) -определению пределов, где абсолютное значение действительных чисел заменяется на абсолютное значение комплексных чисел. С более абстрактной точки зрения, C, наделенный метрикой

- полное метрическое пространство, которое, в частности, включает неравенство треугольника

для любых двух комплексных чисел z 1 и z 2.
Как и в реальном анализе, это понятие сходимости используется для построения ряда элементарных функций : экспоненциальная функция exp (z), также обозначаемая как e, определяется как бесконечная серия

Ряд, определяющий действительные тригонометрические функции синус и косинус, а также гиперболические функции sinh и cosh также переносятся на сложные аргументы без изменений. Для других тригонометрических и гиперболических функций, таких как касательная, все немного сложнее, поскольку определяющие ряды не сходятся для всех комплексных значений. Следовательно, необходимо определить их либо в терминах синуса, косинуса и экспоненты, либо, что то же самое, с помощью метода аналитического продолжения.
формулы Эйлера, который гласит:

для любого действительного числа φ, в частности

В отличие от ситуации с действительными числами, существует бесконечность комплексных решений z уравнения

для любого комплексного числа w ≠ 0. Можно показать, что любое такое решение z - называется комплексным логарифм числа w - удовлетворяет условию

, где arg - это аргумент, определенный выше, и в (действительном) натуральном логарифме. Временной интервал - это многозначная функция, уникальная только с точностью, кратной 2π, log также многозначна. главное значение журнала часто берется путем ограничения мнимой части интервалом (−π, π].
Комплексное возведение в степень z определяется как

и является многозначным, кроме случаев, когда 
Комплексные числа, в отличие от действительные числа, в общем случае, не удовлетворяют требованиям тождеств мощности и логарифма, особенно когда они наивно как однозначные функции; см. отказ от тождеств мощности и логарифма.,, не удовлетворяют удовлетворяют

Обе части уравнения многозначны по определению комплексного возведения в степень, приведенного здесь, а значения слева являются подмножеством значений справа.
Функция f: C→ Cназывается голоморфной, если она удовлетворяет уравнениям Коши - Римана. Например, любую R-линейную карту C→ Cможно записать в виде

с комплексными коэффициентами a и b. Это отображение голоморфно тогда и только тогда, когда b = 0. Второе слагаемое 
Комплексный анализ показывает некоторые особенности, которые не проявляются в реальном анализе. Например, любые две голоморфные функции f и g, которые определяют произвольно малое открытое подмножество из C, обязательно согласовываются везде. Мероморфные функции, функции, которые можно локально записать как f (z) / (z - z 0) с голоморфной функцией f, по-прежнему обладающими некоторыми чертами голоморфных функций. Другие функции имеют особые особенности, например sin (1 / z) при z = 0.
Комплексные числа применяются во многих научных областях, включая обработка сигналов, теория управления, электромагнетизм, гидродинамика, квантовая механика, картография, и анализ вибрации. Некоторые из этих приложений ниже.
Три неколлинеарных точки 


Форма 

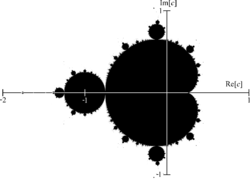 Множество Мандельброта с помеченными реальными и мнимыми осями.
Множество Мандельброта с помеченными реальными и мнимыми осями. Множество Мандельброта - популярный пример фрактала, образованного на комплексной плоскости. Он определяется путем построения каждого местоположения 


Каждый треугольник имеет уникальный эллипс Штейнера - эллипс внутри треугольника и касательный серединам трех сторон треугольника.. фокусы эллипса Штейнера треугольника могут быть найдены следующим образом, согласно теореме Мардена : Обозначим вершины треугольника на комплексной плоскости как a = x A + y A i, b = x B + y B i, и c = x C + y C я. Напишите кубическое уравнение 
 Построение правильного пятиугольника с использованием линейки и циркуля.
Построение правильного пятиугольника с использованием линейки и циркуля.Как упоминалось выше, любое непостоянное полиномиальное уравнение (в комплексных коэффициентах) имеет решение в C . А тем более то же самое верно, если уравнение имеет рациональные коэффициенты. Корни таких уравнений называются алгебраическими числами - они являются основным объектом изучения в теории алгебраических чисел. По сравнению с Q, алгебраическое замыкание Q, которое также содержит все алгебраические числа, C имеет то преимущество, что его легко понять в геометрических терминах. Таким образом, алгебраические методы преподавания, изучение геометрических вопросов и наоборот. С помощью алгебраических методов, более конкретно применяется механизм теории поля к числовому полю, содержащему корни из единицы, можно показать, что невозможно построить правильный безугольник с использованием только циркуля и линейки - геометрическая задача.
Другим примером являются целые числа по Гауссу, то есть есть числа в x + iy, где x и y - целые числа, которые могут использоваться для классификации сумм квадратов.
Аналитическая теория чисел изучает числа, целые или рациональные, используя тот факт, что их можно рассматривать как комплексные числа. Это делается путем кодирования теоретико-числовой информации в комплекснозначных функциях. Например, дзета-функция Римана ζ (s) связана с распределением простых чисел.
В прикладных областях комплексные числа часто используются для вычислений некоторые действительные несобственные интегралы с помощью комплексных функций. Для этого существует несколько методов; см. методы контурного интегрирования.
В дифференциальных уравнениях обычно сначала находят все комплексные корни r линейного уравнения линейное дифференциальное уравнение или систему уравнений, а затем попытаться решить эту систему в терминах функций вида f (t) = e. Аналогично, в разностных уравнениях используются комплексные корни r типического уравнения системы разностных уравнений, чтобы попытаться решить систему в терминах основных функций f (t) = r.
В теории управления системы часто трансформируются из временной области в частотная область с использованием преобразования Лапласа. Затем на комплексной плоскости анализируются нули и полюсы системы . Все методы корневого локуса, графика Найквиста и графика Николса используют комплексную плоскость.
В методе корневого годографа важно, находятся ли нули и полюсы в левой или правой полуплоскости, то есть имеют действительную часть больше или меньше нуля. Если линейная, инвариантная во времени (LTI) система имеет полюса, которые
. Если система имеет нули в правой полуплоскости, это система с неминимальной фазой.
Комплексные числа используются в анализе сигналов и других полях для удобного описания периодически изменяющихся сигналов. Для заданных реальных функций, представляющих реальные физические величины, часто в терминах синусов и косинусов, рассматриваются соответствующие комплексные функции, действительные части которых являются исходными величинами. Для синусоидальной волны заданной частоты абсолютное значение | z | соответствующего z - это амплитуда, а аргумент arg (z) - это фаза.
Если анализ Фурье используется для записи заданного сигнал с действительным знаком как сумма периодических функций, эти периодические функции часто записываются как комплексные функции формы

и

где ω представляет собой угловую частоту, а комплексное число A кодирует фазу и амплитуду, как объяснено выше.
Это использование также распространяется на цифровую обработку сигналов и цифровую обработку изображений, которые используют цифровые версии анализа Фурье (и вейвлет-анализ ). для передачи, сжимать, восстанавливать и иным образом обрабатывать цифровые аудиосигналы, неподвижные изображения и видео сигналы.
Другой пример, относящийся к двум боковым полосам амплитуды модуляции AM-радио, это:

В электротехника, преобразование Фурье используется для анализа различных напряжений и токов. Обработка резисторов, конденсаторов и катушек индуктивности может быть унифицирована путем введения мнимых частотно-зависимых сопротивлений для последних двух и объединения всех трех в один Комплексное число называется импедансом. Этот подход называется векторным исчислением.
В электротехнике мнимая единица обозначается j, чтобы избежать путаницы с I, который обычно используется для обозначения электрический ток, или, более конкретно, i, который обычно используется для обозначения мгновенного электрического тока.
Буква в цепи переменного тока является колебательным, его можно представить как

Для получения измеряемой величины берется действительная часть:
![v (t) = \ mathrm {Re} (V) = \ mathrm {Re} \ left [V_ {0} e ^ {j \ omega t} \ right] = V_ {0} \ cos \ omega t.](https://wikimedia.org/api/rest_v1/media/math/render/svg/b66155dd3cd373aba4b6b5513fc702b0d6274408)
Комплексный сигнал 

В гидродинамике сложные функции используются для описания потенциального потока в двух измерениях..
Поле комплексных чисел характерно для математических квантовой механики, где сложные гильбертовы пространства обеспечивает контекст для одной такой формулировки, которая удобна и пожалуй самый стандартный стандартный. Исходные формулы-основы квантовой механики - уравнение Шредингера и матричная механика Гейзенберга - использовать комплексные числа.
В Специальная теория теории и общей теории теории некоторые формулы для метрики в -времени становятся проще, если временная составляющая пространственно-временного континуума должна быть мнимой. (Этот подход больше не является стандартным в классической теории относительности, но используется в квантовой теории поля.) Комплексные числа необходимы для спиноров, которые составляют обобщение тензоров , используйте в теории относительности.
 График кватернионов Кэли Q8, показывающий циклы умножения на i, jи k
График кватернионов Кэли Q8, показывающий циклы умножения на i, jи kПроцесс расширения поля R вещественных чисел до C известен как конструкция Кэли-Диксона. Он может быть перенесен в более высокие измерения, давая кватоны Hи октонионы O, которые (как реальное настоящее пространство) имеют размерность 4 и 8 соответственно. В этом контексте комплексные числа были названы бинарионами .
. Подобно тому, как при использовании конструкции к действующему числу теряется свойство упорядочивания, свойства, знакомые по действующим и комплексным числам, исчезают с каждым расширением. кватернионы теряют коммутативность, то есть x · y ≠ y · x для некоторых кватернионов x, y, а умножение октонионов, кроме того, что они не коммутативны, не может быть ассоциативным: ( x · y) · z ≠ x · (y · z) для некоторых октонионов x, y, z.
Действительные числа, комплексные числа, кватернионы и октонионы - все это нормированные алгебры с делением над R . По теореме Гурвица они единственные; sedenions, следующий шаг в конструкции Кэли-Диксона, не имеют такой структуры.
Конструкция Кэли-Диксона объединяет с регулярным представлением элементом C, рассматриваемым как R-алгебра (R -векторное пространство с умножением) относительно базиса (1, i). Это означает следующее: R -линейное отображение

для некоторого фиксированного комплексного числа w может быть представлен матрицей 2 × 2 (после выбора базиса). По отношению к базису (1, i) эта матрица имеет вид

то есть, упомянутый в разделе о матричном представлении комплексных чисел выше. Хотя это линейное представление из C в вещественных матрицах 2 × 2, оно не единственное. Любая матрица

обладает тем своим квадратным отрицательным отношением к единичной матрице: J = −I. Тогда

также изоморфен поле C, и дает альтернативную сложную структуру на R . Это обобщается понятием линейной комплексной структуры.
Гиперкомплексные числа также обобщают R, C, Hи O . Например, это понятие содержит комплексные числа с разбиением, которые включают элементы кольца R [x] / (x - 1) (в отличие от R [х] / (х + 1)). В этом кольце уравнение a = 1 имеет четыре решения.
Поле R является завершением Q, поля рациональных чисел, относительно обычного абсолютного значения метрическая. Другой выбор показателей на Q приводит к полям Qpp-адических чисел (для простого числа p), которые тем самым аналогны R . Нет других нетривиальных способов завершения Q, кроме R и Qp, по теореме Островского. Алгебраические замыкания 


Поля R и Qpи их конечные расширения полей, включая C, являются локальными полями.
| Wikimedia Commons имеет носители, относящиеся к Комплексные числа. |
 )
)| Викиверситет имеет ресурсы для изучения Сложные числа |
| Викиучебнике есть книга по теме: Исчисление / Комплексные числа |
| Викиисточник содержит текст статьи Британской энциклопедии 1911 года Число / Комплексные числа. |
 , Princeton University Press, ISBN 978- 0-691-02795-1
, Princeton University Press, ISBN 978- 0-691-02795-1