В математике серия - это сумма члены бесконечной последовательности чисел.
Дана бесконечная последовательность  n-я частичная сумма Sn- это сумма первых n членов последовательности. То есть
n-я частичная сумма Sn- это сумма первых n членов последовательности. То есть

Ряд сходится, если последовательность его частичных сумм  стремится к пределу ; это означает, что частичные суммы становятся все ближе и ближе к заданному числу, когда количество их членов увеличивается. Точнее, ряд сходится, если существует число
стремится к пределу ; это означает, что частичные суммы становятся все ближе и ближе к заданному числу, когда количество их членов увеличивается. Точнее, ряд сходится, если существует число  такое, что для любого произвольно малого положительного числа
такое, что для любого произвольно малого положительного числа  существует (достаточно большое) целое число
существует (достаточно большое) целое число  такое, что для всех
такое, что для всех  ,
,

Если ряд сходится, число  (обязательно уникальное) называется суммой ряда.
(обязательно уникальное) называется суммой ряда.
Любой несходящийся ряд называется расходящимся.
Содержание
- 1 Примеры сходящихся и расходящихся рядов
- 2 Тесты сходимости
- 3 Условная и абсолютная сходимость
- 4 Равномерная сходимость
- 5 Критерий сходимости Коши
- 6 См. Также
- 7 Внешние ссылки
Примеры сходящихся и расходящихся рядов
- Обратные значения натуральных чисел дают расходящийся ряд (гармонический ряд ):

- Чередование знаков обратных положительных целых чисел дает сходящийся ряд (чередующийся гармонический ряд ):

- Обратное значение простых чисел дает расходящийся ряд (таким образом, набор простых чисел является "большим "; см. дивергенция сумма обратных простых чисел ):

- Обратные треугольные числа образуют сходящийся ряд:

- Обратные значения факториалов образуют сходящийся ряд (см. e ):

- Обратное значение квадратных чисел дает сходящийся ряд (Базельская проблема ):

- Величина, обратная степени 2, дает сходящийся ряд (таким образом, набор степеней 2 равен «small »):

- Обратные значения степени любого n>1 образуют сходящийся ряд:

- Чередование знаков, обратных степени 2, также дает сходящийся ряд:

- Чередование знаков, обратных степеням любого n>1, дает сходящийся ряд:

- Обратные значения чисел Фибоначчи дают сходящийся ряд (см. ψ ):

Тесты сходимости
Существует ряд методов определения того, сходится ли ряд или расходится.
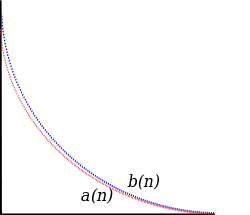
Если можно доказать, что синий ряд

сходится, то меньший ряд

должен сходиться. Напротив, если доказано, что красный ряд

расходится, то

также должны отличаться.
Сравнительный тест. Члены последовательности  сравниваются с членами другой последовательности
сравниваются с членами другой последовательности  . Если,
. Если,
для всех n,  и
и  сходится, затем
сходится, затем 
Однако, если
для всех n,  и
и  расходится, затем
расходится, затем 
Тест отношения. Предположим, что для всех n  не равно нулю. Предположим, что существует
не равно нулю. Предположим, что существует  такое, что
такое, что

Если r < 1, then the series is absolutely convergent. If r>1, то ряд расходится. Если r = 1, тест отношения неубедителен, и ряды могут сходиться или расходиться.
Тест корня или Тест корня n-го уровня . Предположим, что члены рассматриваемой последовательности неотрицательны. Определим r следующим образом:
![r = \ limsup _ {n \ rightarrow \ infty} {\ sqrt [{n}] {| a_ {n} |}},](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd5eebb0f17b1155c0bea36edfdd50d6b9aa0f01)
- где "lim sup" обозначает предел старший (возможно ∞; если предел существует, то это же значение).
Если r < 1, then the series converges. If r>1, то ряд расходится. Если r = 1, проверка корня неубедительна, и ряды могут сходиться или расходиться.
И тест соотношения, и тест корня основаны на сравнении с геометрическим рядом, и поэтому они работают в аналогичных ситуациях. Фактически, если тест соотношения работает (это означает, что предел существует и не равен 1), то также и корневой тест; обратное, однако, неверно. Таким образом, корневой тест применим более широко, но на практике предел часто бывает трудно вычислить для часто встречающихся типов рядов.
Интегральный тест. Ряд можно сравнить с интегралом, чтобы установить сходимость или расхождение. Пусть  - положительная и монотонно убывающая функция. Если
- положительная и монотонно убывающая функция. Если

, то ряд сходится. Но если интеграл расходится, то расходится и ряд.
Тест сравнения пределов. Если  и предел
и предел  существует и не равно нулю, тогда
существует и не равно нулю, тогда  сходится тогда и только тогда, когда
сходится тогда и только тогда, когда  сходится.
сходится.
Тест чередующейся серии. Также известен как тест Лейбница критерий проверка чередующихся серий утверждает, что для чередующихся серий формы  , если
, если  монотонно убывает и имеет предел 0 на бесконечности, затем ряд сходится.
монотонно убывает и имеет предел 0 на бесконечности, затем ряд сходится.
C Испытание на ахий конденсат Если  является положительной монотонно убывающей последовательностью, то
является положительной монотонно убывающей последовательностью, то  сходится тогда и только тогда, когда
сходится тогда и только тогда, когда  сходится.
сходится.
Тест Дирихле
Тест Абеля
Условная и абсолютная сходимость

Иллюстрация абсолютной сходимости степенного ряда Exp [z] вокруг 0, оцененного при z = Exp [⁄ 3 ]. Длина линии конечна.
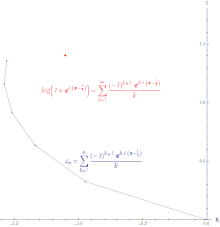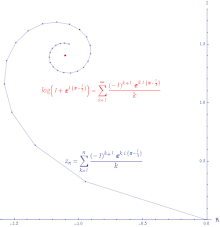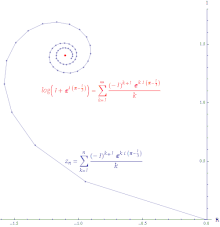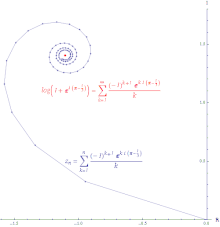
Иллюстрация условной сходимости степенного ряда log (z + 1) вокруг 0, вычисленного при z = exp ((π− ⁄ 3) i). Длина строки бесконечна.
Для любой последовательности  ,
,  для всех n. Следовательно,
для всех n. Следовательно,

Это означает, что если  сходится, затем
сходится, затем  также сходится (но не наоборот).
также сходится (но не наоборот).
Если ряд  сходится, тогда ряд
сходится, тогда ряд  абсолютно сходится. Абсолютно сходящаяся последовательность - это последовательность, в которой длина строки, созданной путем объединения всех приращений в частичную сумму, конечна. Степенный ряд экспоненциальной функции абсолютно сходится везде.
абсолютно сходится. Абсолютно сходящаяся последовательность - это последовательность, в которой длина строки, созданной путем объединения всех приращений в частичную сумму, конечна. Степенный ряд экспоненциальной функции абсолютно сходится везде.
Если ряд  сходится, но ряд
сходится, но ряд  расходится, тогда ряд
расходится, тогда ряд  является условно сходящимся. Путь, образованный соединением частичных сумм условно сходящегося ряда, бесконечно велик. Степенный ряд логарифма условно сходится.
является условно сходящимся. Путь, образованный соединением частичных сумм условно сходящегося ряда, бесконечно велик. Степенный ряд логарифма условно сходится.
В теореме Римана о рядах говорится, что если ряд условно сходится, можно переставить члены ряда таким образом, чтобы ряд сходился к любому значению или даже расходился.
Равномерная сходимость
Пусть  - последовательность функций. Ряд
- последовательность функций. Ряд  , как говорят, сходится равномерно к f, если последовательность
, как говорят, сходится равномерно к f, если последовательность  частичных сумм, определенных как
частичных сумм, определенных как

равномерно сходится к f.
Существует аналог теста сравнения для бесконечного ряда функций, называемый М-тест Вейерштрасса.
критерий сходимости Коши
критерий сходимости Коши утверждает, что ряд

сходится тогда и только тогда, когда последовательность частичных сумм представляет собой последовательность Коши. Это означает, что для каждого  существует положительное целое число
существует положительное целое число  такое, что для всех
такое, что для всех  мы имеем
мы имеем

, что эквивалентно

См. Также
Внешние ссылки
- , Энциклопедия математики, EMS Press, 2001 [1994]
- Weisstein, Eric ( 2005). Теорема о рядах Римана. Проверено 16 мая 2005 г.




















 Если можно доказать, что синий ряд
Если можно доказать, что синий ряд  сходится, то меньший ряд
сходится, то меньший ряд  должен сходиться. Напротив, если доказано, что красный ряд
должен сходиться. Напротив, если доказано, что красный ряд  расходится, то
расходится, то  также должны отличаться.
также должны отличаться. 








![r = \ limsup _ {n \ rightarrow \ infty} {\ sqrt [{n}] {| a_ {n} |}},](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd5eebb0f17b1155c0bea36edfdd50d6b9aa0f01)











 Иллюстрация абсолютной сходимости степенного ряда Exp [z] вокруг 0, оцененного при z = Exp [⁄ 3 ]. Длина линии конечна.
Иллюстрация абсолютной сходимости степенного ряда Exp [z] вокруг 0, оцененного при z = Exp [⁄ 3 ]. Длина линии конечна.  Иллюстрация условной сходимости степенного ряда log (z + 1) вокруг 0, вычисленного при z = exp ((π− ⁄ 3) i). Длина строки бесконечна.
Иллюстрация условной сходимости степенного ряда log (z + 1) вокруг 0, вычисленного при z = exp ((π− ⁄ 3) i). Длина строки бесконечна. 


















