Значение, к которому «стремятся» термины последовательности

Последовательность, заданная периметрами регулярных n-сторонних
многоугольники, описывающие
единичную окружность, имеют предел, равный периметру окружности, т.е.

. Соответствующая последовательность для вписанных многоугольников имеет такой же предел.
| n | n sin (1 / n) |
|---|
| 1 | 0,841471 |
| 2 | 0,958851 |
| ... |
| 10 | 0,998334 |
| ... |
| 100 | 0,999983 |
Поскольку положительное целое  становится все больше и больше, значение
становится все больше и больше, значение  становится произвольно близким к
становится произвольно близким к  . Мы говорим, что «предел последовательности
. Мы говорим, что «предел последовательности  равно
равно  . "
. "
В математике предел последовательности - это значение, к которому «стремятся» члены последовательности , и часто обозначается с помощью  символ (например,
символ (например,  ). Если такой предел существует, последовательность называется сходящейся . Последовательность, которая не сходится, называется расходящейся . Предел последовательности называется фундаментальным понятием, на котором в конечном итоге основан весь математический анализ.
). Если такой предел существует, последовательность называется сходящейся . Последовательность, которая не сходится, называется расходящейся . Предел последовательности называется фундаментальным понятием, на котором в конечном итоге основан весь математический анализ.
Пределы могут быть определены в любой метрике или топологическое пространство, но обычно сначала встречаются в вещественных числах.
Содержание
- 1 История
- 2 Действительные числа
- 2.1 Примеры
- 2.2 Формальное определение
- 2.3 Иллюстрация
- 2.4 Свойства
- 2.5 Бесконечные пределы
- 3 Метрические пространства
- 3.1 Определение
- 3.2 Свойства
- 4 Топологические пространства
- 4.1 Определение
- 4.2 Свойства
- 5 Последовательности Коши
- 6 Определение в гиперреальных числах
- 7 См. Также
- 8 Примечания
- 9 Ссылки
- 10 Внешние ссылки
История
Греческий философ Зенон Элейский известен формулировкой парадоксов, связанных с ограничивающими процессами.
Левкипп, Демокрит, Антифон, Евдокс, и Архимед разработал метод исчерпания, который использует бесконечную последовательность приближения для определения площади или объема. Архимеду удалось суммировать то, что сейчас называется геометрической серией.
Ньютон имел дело с сериями в своих работах по анализу с бесконечными сериями (написанным в 1669 году, распространенным в рукописи, опубликованным в 1711 году), Методом флюксий и бесконечная серия (написана в 1671 году, опубликована в английском переводе в 1736 году, латинский оригинал опубликован гораздо позже) и Tractatus de Quadratura Curvarum (написана в 1693 году, опубликована в 1704 году как приложение к его Optiks). В последней работе Ньютон рассматривает биномиальное разложение (x + o), которое он затем линеаризует, принимая предел, равный 0, стремящемуся к 0.
В 18 веке математики такие как Эйлер сумел суммировать расходящиеся ряды, остановившись в нужный момент; их не очень волновало, существует ли предел, если его можно рассчитать. В конце столетия Лагранж в своей «Теории аналитических функций» (1797) высказал мнение, что отсутствие строгости препятствует дальнейшему развитию математического анализа. Гаусс в своем этюде гипергеометрических рядов (1813) впервые строго исследовал, при каких условиях ряд сходится к пределу.
Современное определение предела (для любого ε существует индекс N, так что...) было дано Бернхардом Больцано (Der binomische Lehrsatz, Прага 1816, мало замеченный в время), и Карлом Вейерштрассом в 1870-х гг.
Действительные числа

График сходящейся последовательности {a n } показан синим цветом. Здесь видно, что последовательность сходится к пределу 0 по мере увеличения n.
В вещественных числах число  равно предел последовательности
равно предел последовательности  , если числа в последовательности становятся все ближе и ближе на
, если числа в последовательности становятся все ближе и ближе на  - а не на какой-либо другой номер.
- а не на какой-либо другой номер.
Примеры
- Если
 для константы c, то
для константы c, то  .
. - Если
 , то
, то  .
. - Если
 when
when  - четное, а
- четное, а  при
при  нечетно, тогда
нечетно, тогда  . (Тот факт, что
. (Тот факт, что  всякий раз, когда
всякий раз, когда  нечетно, не имеет значения.)
нечетно, не имеет значения.) - Для любого действительного числа можно легко построить последовательность, сходящуюся к этому числу, используя десятичные аппроксимации. Например, последовательность
 сходится к
сходится к  . Обратите внимание, что десятичное представление
. Обратите внимание, что десятичное представление  - предел предыдущей последовательности, определяемый как
- предел предыдущей последовательности, определяемый как
 .
.
- Нахождение предела последовательности не всегда очевидно. Два примера:
 (предел которого равен числу e ) и среднее арифметико-геометрическое. Теорема сжатия часто бывает полезна при установлении таких ограничений.
(предел которого равен числу e ) и среднее арифметико-геометрическое. Теорема сжатия часто бывает полезна при установлении таких ограничений.
Формальное определение
Мы называем  предел из последовательности
предел из последовательности  , если выполняется следующее условие:
, если выполняется следующее условие:
- Для каждого вещественное число
 , существует натуральное число
, существует натуральное число  такое, что для каждого натурального число
такое, что для каждого натурального число  , мы имеем
, мы имеем  .
.
Другими словами, для каждой меры близости  , условия последовательности в конечном итоге настолько близки к пределу. Последовательность
, условия последовательности в конечном итоге настолько близки к пределу. Последовательность  называется сходятся к или стремятся к пределу
называется сходятся к или стремятся к пределу  , записывается
, записывается  или
или  .
.
Символически это:

) Если последовательность сходится к некоторому пределу, то она сходящаяся ; в противном случае она расходящаяся . Последовательность, имеющая ноль в качестве предела, иногда называется нулевой последовательностью .
Иллюстрация
Свойства
Пределы последовательностей хорошо себя ведут по отношению к обычным арифметическим операциям. Если  и
и  , то
, то  ,
,  и, если ни b, ни какой-либо
и, если ни b, ни какой-либо  не равно нулю,
не равно нулю,  .
.
Для любой непрерывной функции f, если  , затем
, затем  . Фактически, любая вещественная функция f является непрерывной тогда и только тогда, когда она сохраняет пределы последовательностей (хотя это не обязательно верно при использовании более общих понятий непрерывности).
. Фактически, любая вещественная функция f является непрерывной тогда и только тогда, когда она сохраняет пределы последовательностей (хотя это не обязательно верно при использовании более общих понятий непрерывности).
Некоторые другие важные свойства пределов реальных последовательностей включают следующее (при условии, в каждом уравнении ниже, что пределы справа существуют).
- Предел последовательности уникален.



 при условии
при условии 
![\ lim _ {n \ to \ infty} a_ {n} ^ {p} = \ left [\ lim _ {n \ to \ infty} a_ {n} \ right] ^ {p}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e3649ad26e042284a0fb09b8f674dee7a48b065)
- Если
 для всех
для всех  больше некоторых
больше некоторых  , тогда
, тогда  .
. - (Теорема сжатия ) Если
 для всех
для всех  и
и  , тогда
, тогда  .
. - Если последовательность ограничена и монотонный, то он сходится.
- Последовательность сходится тогда и только тогда, когда каждая подпоследовательность сходится.
- Если каждая подпоследовательность последовательности имеет свою собственную подпоследовательность, которая сходится к той же точке, то исходный se quence сходится к этой точке.
Эти свойства широко используются для доказательства пределов, без необходимости напрямую использовать громоздкое формальное определение. Например. как только доказано, что  , становится легко показать - используя указанные выше свойства - что
, становится легко показать - используя указанные выше свойства - что  (при условии, что
(при условии, что  ).
).
Бесконечные пределы
Последовательность  , как говорят, стремится к бесконечности, записано
, как говорят, стремится к бесконечности, записано  или
или  , если для каждого K существует N такое, что для каждого
, если для каждого K существует N такое, что для каждого  ,
,  ; то есть члены последовательности в конечном итоге больше любого фиксированного K.
; то есть члены последовательности в конечном итоге больше любого фиксированного K.
Аналогично,  , если для каждого K существует N такое, что для каждого
, если для каждого K существует N такое, что для каждого  ,
,
Метрические пространства
Определение
Точка x {\ displaystyle x} метрического пространства (X, d) {\ displaystyle (X, d)}
метрического пространства (X, d) {\ displaystyle (X, d)} - это предел последовательности (xn) {\ displaystyle (x_ {n})}
- это предел последовательности (xn) {\ displaystyle (x_ {n})} если для всех ϵ>0 {\ displaystyle \ epsilon>0}
если для всех ϵ>0 {\ displaystyle \ epsilon>0} , существует N {\ displaystyle N}
, существует N {\ displaystyle N} такой, что для каждого n ≥ N {\ displaystyle n \ geq N}
такой, что для каждого n ≥ N {\ displaystyle n \ geq N} , d (xn, x) < ϵ {\displaystyle d(x_{n},x)<\epsilon }
, d (xn, x) < ϵ {\displaystyle d(x_{n},x)<\epsilon } . Это совпадает с определением, данным для действительных чисел, когда X = R {\ displaystyle X = \ mathbb {R}}
. Это совпадает с определением, данным для действительных чисел, когда X = R {\ displaystyle X = \ mathbb {R}} и d (x, y) = | x - y | {\ displaystyle d (x, y) = | xy |}
и d (x, y) = | x - y | {\ displaystyle d (x, y) = | xy |} .
.
Свойства
Для любой непрерывной функции f, если xn → x {\ displaystyle x_ {n} \ to x} , то f (xn) → f (x) { \ displaystyle f (x_ {n}) \ to f (x)}
, то f (xn) → f (x) { \ displaystyle f (x_ {n}) \ to f (x)} . Фактически, функция f непрерывна тогда и только тогда, когда она сохраняет пределы последовательностей.
. Фактически, функция f непрерывна тогда и только тогда, когда она сохраняет пределы последовательностей.
Пределы последовательностей уникальны, если они существуют, поскольку отдельные точки разделены некоторым положительным расстоянием, поэтому для ϵ {\ displaystyle \ epsilon} меньше половины этого расстояния, последовательность термины не могут находиться на расстоянии ϵ {\ displaystyle \ epsilon}
меньше половины этого расстояния, последовательность термины не могут находиться на расстоянии ϵ {\ displaystyle \ epsilon} от обеих точек.
от обеих точек.
Топологические пространства
Определение
Точка x топологического пространства (X, τ) является пределом последовательности последовательности (xn), если для каждой окрестности U точки x существует N такое, что для каждого n ≥ N {\ displaystyle n \ geq N} , xn ∈ U {\ displaystyle x_ {n } \ в U}
, xn ∈ U {\ displaystyle x_ {n } \ в U} . Это совпадает с определением, данным для метрических пространств, если (X, d) является метрическим пространством и τ {\ displaystyle \ tau}
. Это совпадает с определением, данным для метрических пространств, если (X, d) является метрическим пространством и τ {\ displaystyle \ tau} является топологией, порожденной d.
является топологией, порожденной d.
Предел последовательности точек (xn: n ∈ N) {\ displaystyle \ left (x_ {n}: n \ in \ mathbb {N} \ right) \;} в топологическом пространстве T - это частный случай ограничения функции : домен равен N {\ displaystyle \ mathbb {N}}
в топологическом пространстве T - это частный случай ограничения функции : домен равен N {\ displaystyle \ mathbb {N}} в пространстве N ∪ {+ ∞} {\ displaystyle \ mathbb {N} \ cup \ lbrace + \ infty \ rbrace}
в пространстве N ∪ {+ ∞} {\ displaystyle \ mathbb {N} \ cup \ lbrace + \ infty \ rbrace} , с индуцированной топологией аффинно расширенной системы действительных чисел, диапазон равен T, а аргумент функции n стремится к + ∞, что в этом пространстве является предельной точкой of N {\ displaystyle \ mathbb {N}}
, с индуцированной топологией аффинно расширенной системы действительных чисел, диапазон равен T, а аргумент функции n стремится к + ∞, что в этом пространстве является предельной точкой of N {\ displaystyle \ mathbb {N}} .
.
Свойства
Если X является пространством Хаусдорфа, тогда пределы последовательностей уникальны там, где они существуют. Обратите внимание, что в общем случае это не обязательно; в частности, если две точки x и y топологически неразличимы, то любая последовательность, сходящаяся к x, должна сходиться к y и наоборот.
Последовательности Коши
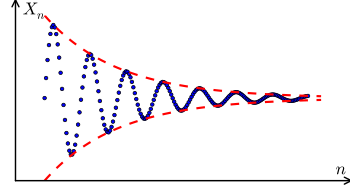
График последовательности Коши (x n), показанный синим цветом, как x n в зависимости от n. Визуально мы видим, что последовательность кажется сходящейся к предельной точке, поскольку члены в последовательности становятся ближе друг к другу по мере увеличения n. В
вещественных числах каждая последовательность Коши сходится к некоторому пределу.
Последовательность Коши - это последовательность, члены которой в конечном итоге становятся произвольно близкими друг к другу после того, как было отброшено достаточно много начальных членов. Понятие последовательности Коши важно при изучении последовательностей в метрических пространствах и, в частности, в реальном анализе. Одним из особенно важных результатов реального анализа является критерий Коши сходимости последовательностей: последовательность действительных чисел сходится тогда и только тогда, когда она является последовательностью Коши. Это остается верным и для других полных метрических пространств.
Определение в гиперреальных числах
Определение предела с помощью гиперреальных чисел формализует интуицию, что для «очень большого» значения индекса соответствующий член «очень близок» к пределу. Точнее, действительная последовательность (xn) {\ displaystyle (x_ {n})} стремится к L, если для каждого бесконечного сверхъестественного H член x H бесконечно близко к L (т. Е. Разность x H - L бесконечно мала ). Эквивалентно L - это стандартная часть x H
стремится к L, если для каждого бесконечного сверхъестественного H член x H бесконечно близко к L (т. Е. Разность x H - L бесконечно мала ). Эквивалентно L - это стандартная часть x H
- L = s t (x H). {\ displaystyle L = {\ rm {st}} (x_ {H}). \,}

Таким образом, предел можно определить по формуле
- lim n → ∞ xn = st (x H), {\ displaystyle \ lim _ {n \ to \ infty} x_ {n} = {\ rm {st}} (x_ {H}),}

где предел существует тогда и только тогда, когда правая часть не зависит от выбор бесконечного H.
См. также
Примечания
Доказательства
Ссылки
- Курант, Ричард (1961). «Дифференциальное и интегральное исчисление, том I», Blackie Son, Ltd., Глазго.
- Фрэнк Морли и Джеймс Харкнесс Трактат по теории функций (New York: Macmillan, 1893)
Внешние ссылки
 Последовательность, заданная периметрами регулярных n-сторонних многоугольники, описывающие единичную окружность, имеют предел, равный периметру окружности, т.е.
Последовательность, заданная периметрами регулярных n-сторонних многоугольники, описывающие единичную окружность, имеют предел, равный периметру окружности, т.е.  . Соответствующая последовательность для вписанных многоугольников имеет такой же предел.
. Соответствующая последовательность для вписанных многоугольников имеет такой же предел. 






 График сходящейся последовательности {a n } показан синим цветом. Здесь видно, что последовательность сходится к пределу 0 по мере увеличения n.
График сходящейся последовательности {a n } показан синим цветом. Здесь видно, что последовательность сходится к пределу 0 по мере увеличения n. 


 для константы c, то
для константы c, то  .
. , то
, то  .
. when
when  - четное, а
- четное, а  при
при  нечетно, тогда
нечетно, тогда  . (Тот факт, что
. (Тот факт, что  всякий раз, когда
всякий раз, когда  нечетно, не имеет значения.)
нечетно, не имеет значения.) сходится к
сходится к  . Обратите внимание, что десятичное представление
. Обратите внимание, что десятичное представление  - предел предыдущей последовательности, определяемый как
- предел предыдущей последовательности, определяемый как .
. (предел которого равен числу e ) и среднее арифметико-геометрическое. Теорема сжатия часто бывает полезна при установлении таких ограничений.
(предел которого равен числу e ) и среднее арифметико-геометрическое. Теорема сжатия часто бывает полезна при установлении таких ограничений.

 такое, что для каждого натурального число
такое, что для каждого натурального число  , мы имеем
, мы имеем  .
.











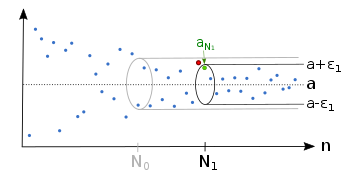




есть лишь конечное число членов последовательности вне эпсилон-трубки.











 при условии
при условии 
![\ lim _ {n \ to \ infty} a_ {n} ^ {p} = \ left [\ lim _ {n \ to \ infty} a_ {n} \ right] ^ {p}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e3649ad26e042284a0fb09b8f674dee7a48b065)
 для всех
для всех  больше некоторых
больше некоторых  , тогда
, тогда  .
. для всех
для всех  и
и  , тогда
, тогда  .
.





























 График последовательности Коши (x n), показанный синим цветом, как x n в зависимости от n. Визуально мы видим, что последовательность кажется сходящейся к предельной точке, поскольку члены в последовательности становятся ближе друг к другу по мере увеличения n. В вещественных числах каждая последовательность Коши сходится к некоторому пределу.
График последовательности Коши (x n), показанный синим цветом, как x n в зависимости от n. Визуально мы видим, что последовательность кажется сходящейся к предельной точке, поскольку члены в последовательности становятся ближе друг к другу по мере увеличения n. В вещественных числах каждая последовательность Коши сходится к некоторому пределу. 

