В математике, тест конденсации Коши, названный в честь Огюстена-Луи Коши, это стандартный тест сходимости для бесконечной серии. Для невозрастающей последовательности  неотрицательных действительных чисел, серия
неотрицательных действительных чисел, серия  сходится тогда и только тогда, когда "сжатый" ряд
сходится тогда и только тогда, когда "сжатый" ряд  сходится. Более того, если они сходятся, сумма сжатого ряда не более чем в два раза больше суммы исходного.
сходится. Более того, если они сходятся, сумма сжатого ряда не более чем в два раза больше суммы исходного.
Содержание
- 1 Оценка
- 2 Интегральное сравнение
- 3 Примеры
- 4 Обобщение Шлёмильха
- 5 Ссылки
- 6 Внешние ссылки
Оценка
Конденсация Коши тест следует из более сильной оценки,

, которое следует понимать как неравенство расширенных действительных чисел. Далее следует основная направленность доказательства, построенного по образцу доказательства Оремом дивергенции гармонических рядов.
. Чтобы увидеть первое неравенство, члены исходного ряда заменены скобками на серии, длины которых являются степенями из двух, а затем каждый прогон ограничивается сверху заменой каждого члена на самый большой член в этом прогоне. Этот член всегда является первым, поскольку предполагается, что члены не увеличиваются.

Чтобы увидеть второе неравенство, эти две серии снова заменены скобками на прогоны степеней двойной длины, но «смещение», как показано ниже, так что прогон  , который начинается с
, который начинается с  совпадает с концом цикла
совпадает с концом цикла  который заканчивается на
который заканчивается на  , так что первый всегда остается «впереди» второго.
, так что первый всегда остается «впереди» второго.

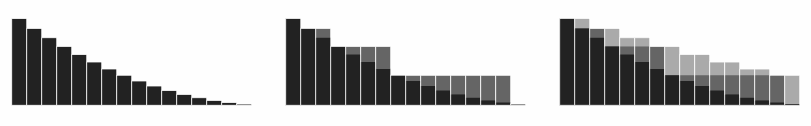
Визуализация приведенного выше аргумента. Частичные суммы ряда

,

и

показаны с наложением слева направо.
Интеграл сравнение
Преобразование «уплотнение»  вызывает подстановку интегральной переменной
вызывает подстановку интегральной переменной  с получением
с получением  .
.
Реализация этой идеи, интегральный тест на сходимость дает нам в случае монотонного f, что  сходится тогда и только тогда, когда
сходится тогда и только тогда, когда  сходится. Замена
сходится. Замена  дает интеграл
дает интеграл  и другой интегральный тест приводит нас к сжатому ряду
и другой интегральный тест приводит нас к сжатому ряду  .
.
Примеры
Тест может быть полезен для серий, где n появляется в знаменателе в f. Самый простой пример такого рода - гармонический ряд  преобразуется в ряд
преобразуется в ряд  , который явно расходится.
, который явно расходится.
В качестве более сложного примера возьмем
 .
.
Здесь ряд определенно сходится при a>1 и расходится при a < 1. When a = 1, the condensation transformation gives the series
 .
.
Логарифмы «сдвигаются влево». Таким образом, когда a = 1, мы имеем сходимость для b>1, расходимость для b < 1. When b = 1 the value of c enters.
Этот результат легко обобщается: многократно применяемый тест конденсации может использоваться, чтобы показать, что для  , обобщенный ряд Бертрана
, обобщенный ряд Бертрана

сходится для  и расходится для
и расходится для  . Здесь
. Здесь  обозначает m-ю композиционную итерацию функции
обозначает m-ю композиционную итерацию функции  , так что
, так что

Нижний предел суммы,  , был выбран таким образом что все члены серии положительны. Примечательно, что эти ряды предоставляют примеры бесконечных сумм, которые сходятся или расходятся сколь угодно медленно. Например, в случае
, был выбран таким образом что все члены серии положительны. Примечательно, что эти ряды предоставляют примеры бесконечных сумм, которые сходятся или расходятся сколь угодно медленно. Например, в случае  и
и  частичное сумма превышает 10 только после
частичное сумма превышает 10 только после  (a googolplex ) терминов; тем не менее, серии расходятся.
(a googolplex ) терминов; тем не менее, серии расходятся.
Обобщение Шлёмильха
Пусть u (n) будет строго возрастающей последовательностью положительных целых чисел, так что отношение последовательных разностей ограничено: существует положительное действительное число N, для которого:

Тогда при условии, что  удовлетворяет тем же предварительным условиям, что и в тесте Коши, сходимость ряда
удовлетворяет тем же предварительным условиям, что и в тесте Коши, сходимость ряда  эквивалентно сходимости:
эквивалентно сходимости:

Принимая  так, что
так, что  , тест конденсации Коши является частным случаем.
, тест конденсации Коши является частным случаем.
Ссылки
- Бонар, Хури (2006). Настоящая бесконечная серия. Математическая ассоциация Америки. ISBN 0-88385-745-6.
Внешние ссылки










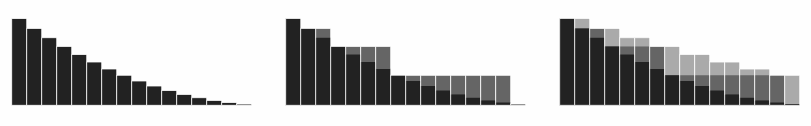 Визуализация приведенного выше аргумента. Частичные суммы ряда
Визуализация приведенного выше аргумента. Частичные суммы ряда  ,
,  и
и  показаны с наложением слева направо.
показаны с наложением слева направо. 









 .
. .
.













