Войти
Решетчатая диаграмма Q примыкает к положительным квадратным корням из 2 и 3, ее подполя и группы Галуа. В математике, теория Галуа обеспечивает связь между теорией поля и теорией групп. Используя теорию Галуа, некоторые проблемы теории поля можно свести к теории групп, которая в некотором смысле проще и понятнее. Он использовался для решения классических задач, включая демонстрацию того, что две проблемы древности не могут быть решены, как они были заявлены (удвоение куба и деление угла пополам); показывающий, что не существует формулы пятой степени ; и показывает, какие многоугольники могут быть построены.
Объект назван в честь Эвариста Галуа, который ввел его для изучения корней полинома и характеристики полиномиальные уравнения, которые разрешимы радикалами в терминах свойств группы перестановок их корней - уравнение разрешимо радикалами, если его корни могут быть выражены формулой, включающей только целые числа, корни n-й степени и четыре основных арифметических операции.
Теория была популяризирована среди математиков и разработана Ричардом Дедекиндом, Леопольд Кронекер, Эмиль Артин и другие, которые интерпретировали группу перестановок корней как группу автоморфизмов расширения поля.
Теория Галуа была обобщена на Связи Галуа и Теорию Галуа Гротендика.
Рождение и развитие теории Галуа было вызвано следующим вопросом, который был одним из основных открытых математических вопросов до начала 19 века:
Существует ли формула для корней Полиномиальное уравнение пятой (или более высокой) степени в терминах коэффициентов полинома с использованием только обычных алгебраических операций (сложение, вычитание, умножение, деление) и применения радикалов (квадратные корни, кубические корни и т. д.)?
Теорема Абеля – Руффини дает контрпример, доказывающий, что существуют полиномиальные уравнения f или которых такая формула не может существовать. Теория Галуа дает гораздо более полный ответ на этот вопрос, объясняя, почему можно решить некоторые уравнения, включая все уравнения четвертой степени или ниже, указанным выше способом и почему это невозможно для большинства уравнений пятой степени. или выше. Кроме того, он обеспечивает средство определения возможности решения конкретного уравнения, которое является концептуально ясным и легко выражается в виде алгоритма.
Теория Галуа также дает ясное представление о вопросах, касающихся проблем в компасе и линейка конструкция. Он дает элегантную характеристику соотношений длин, которые могут быть построены с помощью этого метода. Используя это, становится относительно легко ответить на такие классические задачи геометрии, как
Галуа 'теория возникла при изучении симметрических функций - коэффициенты одночлена являются (с точностью до знака) элементарными симметричными многочленами в корнях. Например, (x - a) (x - b) = x - (a + b) x + ab, где 1, a + b и ab - элементарные многочлены степени 0, 1 и 2 от двух переменных.
Впервые это было формализовано французским математиком XVI века Франсуа Виетом в формулах Вьете для случая положительных действительных корней. По мнению британского математика XVIII века Чарльза Хаттона, выражение коэффициентов многочлена через корни (не только для положительных корней) впервые было понято французским математиком XVII века Альбер Жирар ; Хаттон пишет:
... [Жирар] был] первым человеком, который понял общую доктрину образования коэффициентов степеней из суммы корней и их произведений. Он был первым, кто открыл правила суммирования степеней корней любого уравнения.
Таким образом, дискриминант является симметричной функцией в корнях, которая отражает свойства корней - это нуль тогда и только тогда, когда многочлен имеет кратный корень, а для квадратичных и кубических многочленов он положителен тогда и только тогда, когда все корни действительны и различные, и отрицателен тогда и только тогда, когда существует пара различных комплексно сопряженных корней. Подробнее см. Дискриминант: Природа корней.
Кубика была впервые частично решена итальянским математиком 15–16 веков Сципионе дель Ферро, который, однако, не опубликовал свои результаты; этот метод, однако, решал только один тип кубического уравнения. Это решение было затем независимо открыто заново в 1535 году Никколо Фонтана Тарталья, который поделился им с Джероламо Кардано, попросив его не публиковать его. Затем Кардано распространил это на множество других случаев, используя аналогичные аргументы; подробнее см. Метод Кардано. После открытия работы дель Ферро он почувствовал, что метод Тартальи больше не является секретом, и поэтому опубликовал свое решение в своей книге 1545 Ars Magna. Его ученик Лодовико Феррари решил многочлен четвертой степени; его решение также было включено в Ars Magna. В этой книге, однако, Кардано не предоставил «общую формулу» для решения кубического уравнения, поскольку в его распоряжении не было ни комплексных чисел, ни алгебраической системы обозначений, чтобы описать общее кубическое уравнение. Благодаря современным обозначениям и комплексным числам формулы в этой книге работают в общем случае, но Кардано этого не знал. Рафаэль Бомбелли сумел понять, как работать с комплексными числами для решения всех форм кубического уравнения.
Следующим шагом стала статья 1770 года «Рефлексии на основе решения алгебры уравнений» французско-итальянского математика Жозефа Луи Лагранжа в его методе резольвент Лагранжа, где он проанализировал решения Кардано и Феррари для кубик и квартик, рассматривая их с точки зрения перестановок корней, что дало вспомогательный многочлен более низкой степени, обеспечивая единое понимание решений и закладывая основу для теории групп и теории Галуа. Однако принципиально то, что он не рассматривал композицию перестановок. Метод Лагранжа не распространяется на уравнения пятой степени и выше, поскольку резольвента имеет более высокую степень.
У квинтики почти не было общих решений радикалами Паоло Руффини в 1799 году, чья основная идея заключалась в использовании групп перестановок, а не просто одной перестановки. Его решение содержало пробел, который Коши считал незначительным, хотя он не был исправлен до работы норвежского математика Нильса Хенрика Абеля, который опубликовал доказательство в 1824 году, тем самым установив теорему Абеля – Руффини..
Хотя Руффини и Абель установили, что общая квинтика не может быть решена, некоторые частные квинтики могут быть решены, например, x - 1 = 0, и точный критерий, по которому данный многочлен пятой или более высокой степени может быть определен как разрешимый или нет было дано Эваристом Галуа, который показал, что вопрос о том, был ли многочлен разрешимым или нет, было эквивалентно тому, является ли группа перестановок его корней - в современных терминах, его группа Галуа - имели определенную структуру - говоря современным языком, была ли это разрешимая группа. Эта группа всегда была разрешима для многочленов четвертой или меньшей степени, но не всегда так для многочленов пятой и большей степени, что объясняет, почему не существует общего решения для более высоких степеней.
Портрет Эвариста Галуа в возрасте около 15 лет В 1830 году Галуа (в возрасте 18 лет) подал в Парижскую академию наук мемуары о своем теория разрешимости радикалами; В 1831 году статья Галуа была окончательно отвергнута как слишком схематичная и дававшая условие в терминах корней уравнения, а не его коэффициентов. Затем Галуа умер на дуэли в 1832 году, и его статья «Mémoire sur les conditions de résolubilité des équations par radicaux» оставалась неопубликованной до 1846 года, когда она была опубликована Жозефом Лиувиллем вместе с некоторыми из его собственных объяснений.. Перед этой публикацией Лиувилль объявил Академии о результатах Галуа в речи, которую он произнес 4 июля 1843 года. По словам Аллана Кларка, характеристика Галуа «кардинально заменяет работы Абеля и Руффини».
Теория Галуа была общеизвестно трудной для понимания его современниками, особенно до того уровня, на котором они могли ее расширить. Например, в своем комментарии 1846 года Лиувилль полностью упустил теоретико-групповое ядро метода Галуа. Джозеф Альфред Серре, присутствовавший на некоторых выступлениях Лиувилля, включил теорию Галуа в свой (третье издание) своего 1866 года. учебник Cours d'algèbre supérieure. Ученик Серре, Камилла Джордан, имел еще лучшее понимание, что отражено в его книге 1870 года «Traité des replaces et des équations algébriques». За пределами Франции теория Галуа долгое время оставалась более неясной. В Великобритании Кэли не смог понять ее глубины, и популярные британские учебники по алгебре даже не упоминали теорию Галуа до конца столетия. В Германии работы Кронекера были больше сосредоточены на результате Абеля. Дедекинд мало писал о теории Галуа, но читал лекции по ней в Геттингене в 1858 году, продемонстрировав очень хорошее понимание. Книги 1880-х годов Эжена Нетто, основанные на чертах Иордании, сделали теорию Галуа доступной для более широкого круга лиц. Немецкая и американская аудитория, а также Учебник по алгебре Генриха Мартина Вебера 1895 года.
Учитывая полином, возможно, что некоторые из корни связаны различными алгебраическими уравнениями. Например, может случиться так, что для двух корней, скажем A и B, A + 5B = 7. Центральная идея теории Галуа состоит в рассмотрении перестановок (или перестановок) корней, таких как что любое алгебраическое уравнение, которому удовлетворяют корни, по-прежнему выполняется после того, как корни переставлены. Первоначально теория была разработана для алгебраических уравнений с коэффициентами рациональных чисел. Он естественным образом распространяется на уравнения с коэффициентами в любом поле , но это не будет рассматриваться в простых примерах ниже.
Эти перестановки вместе образуют группу перестановок, также называемую группой Галуа полинома, которая подробно описывается в следующих примерах.
Рассмотрим квадратное уравнение
Используя квадратную формулу , мы находим, что два корня равны
Выполнены примеры алгебраических уравнений на A и B включают
и
Если мы поменяем местами A и B в любом из последних двух уравнений, мы получаем другое истинное утверждение. Например, уравнение A + B = 4 становится B + A = 4. В более общем смысле верно, что это справедливо для всех возможных алгебраических отношений между A и B, таких что все коэффициенты рациональны ; то есть в любом таком отношении замена A и B дает другое истинное отношение. Это является результатом теории симметричных многочленов, которые в этом случае могут быть заменены манипуляциями с формулами с использованием биномиальной теоремы. (Можно возразить, что A и B связаны алгебраическим уравнением A - B - 2√3 = 0, которое не остается верным, когда A и B меняются местами. Однако это соотношение здесь не рассматривается, потому что оно имеет коэффициент −2√3, что нерационально.)
Мы заключаем, что группа Галуа многочлена x - 4x + 1 состоит из двух перестановок: тождества перестановки который оставляет A и B нетронутыми, и перестановку транспонирования, которая меняет местами A и B. Это циклическая группа второго порядка, и поэтому изоморфна Z/2Z.
Аналогичное обсуждение применимо к любому квадратичному многочлену ax + bx + c, где a, b и c - рациональные числа.
Рассмотрим многочлен
который также может записывается как
Мы хотим описать группу Галуа этого полинома снова над полем рациональных чисел. У многочлена четыре корня:
Там есть 24 возможных способа перестановки этих четырех корней, но не все эти перестановки являются членами группы Галуа. Члены группы Галуа должны сохранять любое алгебраическое уравнение с рациональными коэффициентами, содержащими A, B, C и D.
Среди этих уравнений мы имеем:
Отсюда следует, что если φ - перестановка, принадлежащая Галуа группы, должно быть:
Это означает, что перестановка корректно определяется образом A и что функция Галуа В группе 4 элемента:
Это означает, что группа Галуа изоморфна четырехгруппе Клейна.
В современном подходе каждый начинает с расширение поля L / K (читается «L над K») и исследует группу автоморфизмов L, которые фиксируют K. Подробнее см. статью о группах Галуа объяснение и примеры.
Связь между двумя подходами заключается в следующем. Коэффициенты рассматриваемого полинома следует выбирать из базового поля K. Верхнее поле L должно быть полем, полученным путем присоединения корней рассматриваемого полинома к базовому полю. Любая перестановка корней, которая уважает алгебраические уравнения, как описано выше, приводит к автоморфизму L / K, и наоборот.
В первом примере выше мы изучали расширение Q (√3) / Q, где Q - это поле рациональные числа, а Q (√3) - это поле, полученное из Q путем присоединения к √3. Во втором примере мы изучали расширение Q (A, B, C, D) / Q.
. У современного подхода есть несколько преимуществ перед подходом группы перестановок.
Понятие разрешимой группы в теории групп позволяет определить, разрешимо ли многочлен в радикалах, в зависимости от того, обладает ли его группа Галуа свойством разрешимости. По существу, каждое расширение поля L / K соответствует факторной группе в композиционной серии группы Галуа. Если фактор-группа в композиционном ряду является циклической порядка n, и если в соответствующем расширении поля L / K поле K уже содержит примитивный корень n-й степени из единицы, то она является радикальным расширением, и тогда элементы L могут быть выражены с помощью корня n-й степени некоторого элемента K.
Если все фактор-группы в ее композиционном ряду циклические, группа Галуа называется разрешимой, и все элементов соответствующего поля можно найти путем многократного извлечения корней, произведений и сумм элементов из базового поля (обычно Q ).
Одним из величайших триумфов теории Галуа было доказательство того, что для любого n>4 существуют многочлены степени n, не разрешимые в радикалах (это было независимо доказано с использованием аналогичного метода с помощью Niels Henrik Abel несколькими годами ранее, и это теорема Абеля – Руффини ), а также систематический способ проверки того, разрешима ли конкретный многочлен в радикалах. Теорема Абеля – Руффини вытекает из того факта, что при n>4 симметрическая группа Snсодержит простую, нециклическую, нормальную подгруппу, а именно альтернированную группа An.
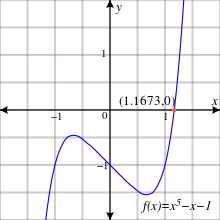Для многочлена f (x) = x - x - 1 единственный действительный корень x = 1.1673... является алгебраическим, но не выражается в терминах радикалов. Остальные четыре корня - это комплексные числа.Ван дер Варден цитирует многочлен f (x) = x - x - 1. По теореме о рациональном корне у него нет рациональных нулей. У нее также нет линейных множителей по модулю 2 или 3.
Группа Галуа функции f (x) по модулю 2 является циклической группой порядка 6, потому что f (x) по модулю 2 делится на многочлены порядков 2 и 3, ( х + х + 1) (х + х + 1).
f (x) по модулю 3 не имеет линейного или квадратичного множителя и, следовательно, неприводима. Таким образом, ее группа Галуа по модулю 3 содержит элемент порядка 5.
Известно, что группа Галуа по простому модулю изоморфна подгруппе группы Галуа над рациональными числами. Группа перестановок на 5 объектах с элементами порядков 6 и 5 должна быть симметрической группой S 5, которая, следовательно, является группой Галуа для f (x). Это один из простейших примеров неразрешимого полинома пятой степени. Согласно Сержу Лангу, Эмиль Артин нашел этот пример.
Обратная задача Галуа - найти расширение поля с учитывая группу Галуа.
Пока не указано также основное поле, проблема не очень сложна, и все конечные группы действительно встречаются как группы Галуа. Чтобы показать это, можно поступить следующим образом. Выберите поле K и конечную группу G. Теорема Кэли говорит, что G является (с точностью до изоморфизма) подгруппой симметрической группы S на элементах G. Выберите неопределенные {x α }, по одному для каждого элемента α группы G, и присоедините их к K, чтобы получить поле F = K ({x α }). Внутри F содержится поле L симметричных рациональных функций в {x α }. Группа Галуа группы F / L - это S согласно основному результату Эмиля Артина. G действует на F ограничением действия S. Если фиксированным полем этого действия является M, то по основной теореме Галуа группа Галуа группы F / M является G.
С другой стороны, это открытый вопрос, является ли каждая конечная группа группой Галуа расширения поля поля Q рациональных чисел. Игорь Шафаревич доказал, что всякая разрешимая конечная группа является группой Галуа некоторого расширения Q . Различные люди решили обратную задачу Галуа для выбранных неабелевых простых групп. Существование решений было показано для всех, кроме, возможно, одной (группа Матье M23) из 26 спорадических простых групп. Существует даже многочлен с целыми коэффициентами, группа Галуа которого является группой Монстров.
 | Посмотрите Теория Галуа в Викисловаре, бесплатном словаре. |
 | На Викискладе есть материалы, связанные с теорией Галуа. |
Некоторые онлайн-руководства по Теория Галуа опубликована по адресу:
Интернет-учебники на французском, немецком, итальянском и английском языках можно найти по адресу:
