В теории групп, ветвь абстрактной алгебры, циклическая группа или моногенная группа - это группа, которая сгенерирована одним элементом. То есть это набор из обратимых элементов с единственной ассоциативной двоичной операцией, и он содержит элемент g такой, что каждый другой элемент группы может быть получен путем многократного применения групповой операции к g или ее обратной. Каждый элемент может быть записан как степень g в мультипликативной записи или как кратное g в аддитивной записи. Этот элемент g называется генератором группы.
Каждая бесконечная циклическая группа изоморфна аддитивной группе из Z, целые числа. Каждая конечная циклическая группа порядка n изоморфна аддитивной группе Z/nZ целых чисел по модулю n. Каждая циклическая группа является абелевой группой (что означает, что ее групповая операция коммутативна ), и каждая конечно порожденная абелева группа является прямым продуктом циклических групп.
Каждая циклическая группа порядка простого является простой группой, которая не может быть разбита на более мелкие группы. В классификации конечных простых групп один из трех бесконечных классов состоит из циклических групп простого порядка. Таким образом, циклические группы простого порядка входят в число строительных блоков, из которых могут быть построены все группы.
 Шесть 6-го комплексного корня из единицы образуют циклическую группу при умножении. Здесь z - генератор, а z - нет, потому что его мощности не дают нечетных степеней z.
Шесть 6-го комплексного корня из единицы образуют циклическую группу при умножении. Здесь z - генератор, а z - нет, потому что его мощности не дают нечетных степеней z. Для любого элемента g в любой группе G можно сформировать подгруппу всех целочисленных степеней ⟨ g⟩ = {g | k ∈ Z }, называемая циклической подгруппой группы g. порядок в g - это количество элементов в ⟨g⟩; то есть порядок элемента равен порядку его циклической подгруппы.
Циклическая группа - это группа, которая равна одной из ее циклических подгрупп: G = ⟨g⟩ для некоторого элемента g, называемого генератором.
Для конечной циклической группы G порядка n, мы имеем G = {e, g, g,..., g}, где e - единичный элемент, а g = g всякий раз, когда i ≡ j (mod n); в частности, g = g = e и g = g. Абстрактная группа, определяемая этим умножением, часто обозначается C n, и мы говорим, что G изоморфна стандартной циклической группе C n. Такая группа также изоморфна Z/nZ, группе целых чисел по модулю n с операцией сложения, которая является стандартной циклической группой в аддитивной записи. При изоморфизме χ, определяемом формулой χ (g) = i, единичный элемент e соответствует 0, произведения соответствуют суммам, а степени соответствуют кратным.
Например, набор комплексных корней 6-й степени из единицы
образует группу при умножении. Он циклический, так как порождается первообразным корнем 
Вместо этого из частных обозначений Z/nZ, Z/ (n) или Z / n, некоторые авторы обозначают конечную циклическую группу как Zn, но это противоречит обозначению теория чисел, где Zpобозначает кольцо p-адических чисел, или локализация в первичном идеале.
.
| p1, (* ∞∞ ) | p11g, (22∞) |
|---|---|
 |  |
| Две группы фризов изоморфны Z . С одним генератором p1 имеет трансляции, а p11g - скользящие отражения. | |
С другой стороны, в бесконечной циклической группе G = ⟨g⟩, степени g дают различные элементы для всех целых чисел k, так что G = {..., g, g, e, g, g,...}, и G изоморфна стандартной группе C = C ∞ и Z, аддитивной группе целых чисел. Пример первая группа фризов. Здесь нет конечных циклов, и название «циклический» может быть неверным
Чтобы избежать этой путаницы, Бурбаки ввел термин моногенная группа для группы с одним образующим и ограничил «циклическую группу» для обозначения конечной моногенной группы, избегая термина «бесконечная циклическая группа».
 |  |  |
| C1 | C2 | C3 |
|---|---|---|
 |  |  |
| C4 | C5 | C6 |
Набор целых чисел Zс операция сложения образует группу. Это бесконечная циклическая группа, потому что все целые числа могут быть записаны путем многократного добавления или вычитания единственного числа 1. В этой группе 1 и -1 являются единственными образующими. Каждая бесконечная циклическая группа изоморфна Z.
. Для любого положительного целого числа n набор целых чисел по модулю n, снова с помощью операции сложения, образует конечную циклическую группу, обозначенную Z/nZ. Модульное целое число i является генератором этой группы, если i относительно простого с n, потому что эти элементы могут генерировать все другие элементы группы посредством сложения целых чисел. (Число таких образующих равно φ (n), где φ - функция Эйлера.) Каждая конечная циклическая группа G изоморфна Z/nZ, где n = | G | это порядок группы.
Операции сложения целых чисел и модульных целых чисел, используемые для определения циклических групп, являются операциями сложения коммутативных колец, также обозначаемых Z и Z/nZили Z / (n). Если p является простым, то Z/pZявляется конечным полем и обычно обозначается Fpили GF (p) для поля Галуа.
Для каждого положительного целого числа n набор целых чисел по модулю n, взаимно простых с n, записывается как (Z/nZ); он образует группу при операции умножения. Эта группа не всегда циклическая, но это так, когда n равно 1, 2, 4, степень нечетного простого числа или удвоенная степень нечетного простого числа (последовательность A033948 в OEIS ). Это мультипликативная группа единиц кольца Z/nZ; имеется φ (n) из них, где φ снова функция Эйлера. Например, (Z/6Z) = {1,5}, а поскольку 6 дважды нечетное простое число, это циклическая группа. Напротив, (Z/8Z) = {1,3,5,7} является 4-группой Клейна и не является циклической. Когда (Z/nZ) является циклическим, его генераторы называются примитивными корнями по модулю n.
Для простого числа p группа (Z/pZ) всегда циклическая, состоящая из ненулевых элементов конечное поле порядка p. В более общем смысле, каждая конечная подгруппа мультипликативной группы любого поля является циклической.
Набор вращательных симметрий из многоугольника образует конечную циклическую группу. Если существует n различных способов перемещения многоугольника к себе посредством поворота (включая нулевое вращение), то эта группа симметрии изоморфна Z/nZ. В трех или более высоких измерениях существуют другие группы конечной симметрии, которые являются циклическими, но не все вращения вокруг оси, а вместо этого вращательные отражения.
Группа всех вращений круг S (круг группа, также обозначаемый S) не является циклическим, потому что не существует единственного вращения, целые степени которого генерируют все вращения. Фактически, бесконечная циклическая группа C ∞ счетна, а S - нет. Группа поворотов на рациональные углы счетна, но все же не циклическая.
n-й корень из единицы - это комплексное число, n-я степень которого равна 1, корень из полином x - 1. Множество всех корней n-й степени из единицы образуют циклическую группу порядка n при умножении. Например, многочлен z - 1 множится как (z - 1) (z - ω) (z - ω), где ω = e; множество {1, ω, ω} = {ω, ω, ω} образует циклическую группу относительно умножения. Группа Галуа из расширения поля рациональных чисел, порожденных корнями n-й степени из единицы, образует другую группу, изоморфную мультипликативной группе (Z/nZ) порядка φ (n), который является циклическим для некоторых, но не для всех n (см. выше).
Расширение поля называется циклическим расширением, если его группа Галуа является циклической. Для полей нулевой характеристики такие расширения являются предметом теории Куммера и тесно связаны с разрешимостью с помощью радикалов. Для расширения конечных полей характеристики p его группа Галуа всегда конечна и циклическая, порожденная степенью отображения Фробениуса. Наоборот, для данного конечного поля F и конечной циклической группы G существует конечное расширение поля F, группа Галуа которого равна G.
Все подгруппы и Факторгруппы циклических групп являются циклическими. В частности, все подгруппы Z имеют форму ⟨m⟩ = m Z, где m - положительное целое число. Все эти подгруппы отличаются друг от друга, и, за исключением тривиальной группы {0} = 0 Z, все они изоморфны Z . Решетка подгрупп группы Z изоморфна двойственной решётке натуральных чисел, упорядоченных по делимости. Таким образом, поскольку простое число p не имеет нетривиальных делителей, p Z является максимальной собственной подгруппой, а фактор-группа Z/pZявляется простой ; на самом деле циклическая группа проста тогда и только тогда, когда ее порядок простой.
Все фактор-группы Z/nZконечны, за исключением Z/0Z= Z/ {0}. Для каждого положительного делителя d числа n фактор-группа Z/nZимеет ровно одну подгруппу порядка d, порожденную классом вычетов числа n / d. Других подгрупп нет.
Каждая циклическая группа абелева. То есть его групповая операция коммутативна : gh = hg (для всех g и h в G). Это ясно для групп целочисленного и модульного сложения, поскольку r + s ≡ s + r (mod n), и это следует для всех циклических групп, поскольку все они изоморфны этим стандартным группам. Для конечной циклической группы порядка n g является единицей для любого элемента g. Это снова следует с помощью изоморфизма модульного сложения, поскольку kn ≡ 0 (mod n) для любого целого числа k. (Это также верно для общей группы порядка n из-за теоремы Лагранжа.)
Для степени простого p группа Z/pZназывается первичная циклическая группа. Основная теорема абелевых групп утверждает, что каждая конечно порожденная абелева группа является конечным прямым произведением примарных циклических и бесконечных циклических групп.
Поскольку циклическая группа абелева, каждый из ее классов сопряженности состоит из одного элемента. Следовательно, циклическая группа порядка n имеет n классов сопряженности.
Если d является делителем числа n, то количество элементов в Z/nZ, имеющих порядок d, равно φ (d), а количество элементов, порядок которых делит d, равно точно d. Если G - конечная группа, в которой для каждого n>0 G содержит не более n элементов порядка, делящего n, то G должна быть циклической. Порядок элемента m в Z/nZравен n / gcd (n, m).
Если n и m являются взаимно простыми, то прямое произведение двух циклических групп Z/nZи Z/mZизоморфно циклической группе Z / nm Z, и обратное также верно: это одна из форм китайской теоремы об остатках. Например, Z / 12 Z изоморфно прямому произведению Z/3Z× Z/4Zпри изоморфизме (k mod 12) → (k mod 3, k mod 4); но он не изоморфен Z/6Z× Z/2Z, в котором каждый элемент имеет порядок не выше 6.
Если p является простым числом, то любая группа с p элементами изоморфна простому группа Z/pZ. Число n называется циклическим числом, если Z/nZявляется единственной группой порядка n, что верно именно тогда, когда gcd (n, φ (n)) = 1. Циклические числа включают в себя все простые числа, но некоторые из них являются составными, например 15. Однако все циклические числа нечетные, кроме 2. Циклические числа:
Из определения немедленно следует, что циклические группы имеют представление группы C∞= ⟨x |⟩ и C n = ⟨x | x⟩ для конечного n.
Теория представлений циклической группы является критическим базовым случаем для теории представлений более общих конечных групп.>сложный случай, представление циклической группы разлагается в прямую сумму линейных персонажей, что делает прозрачной связь между теорией персонажей и теорией репрезентации. В положительном характеристическом случае неразложимые представления циклической группы образуют модель и индуктивную основу теории представлений групп с циклическими силовскими подгруппами и в более общем плане теории представлений блоков циклический дефект.
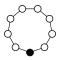
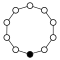
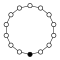
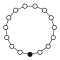
A График циклов иллюстрирует различные циклы группы и особенно полезен при визуализации структуры небольших конечных групп. Граф циклов для циклической группы - это просто круговой граф , где порядок группы равен количеству узлов. Один генератор определяет группу как направленный путь на графике, а обратный генератор определяет обратный путь. Тривиальные пути (идентичность) можно нарисовать как цикл , но обычно они подавляются. Z 2 иногда рисуется с двумя изогнутыми краями как мультиграф.
Циклические группы Z n, порядок n, представляет собой один цикл, изображенный на графике просто как n-сторонний многоугольник с элементами в вершинах. Когда n = ab, где a и b являются относительно простыми (т.е. gcd (a, b) = 1), циклическая группа Z n может быть разложена в прямой продукт Za× Z b.
 |  |  |  |  |  |  | |
| Z1 | Z2 | Z3 | Z4 | Z5 | Z6= Z 3×Z2 | Z7 | Z8 |
 |  |  |  |  |  |  | 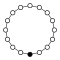 |
| Z9 | Z10= Z 5×Z2 | Z11 | Z12= Z 4×Z3 | Z13 | Z14= Z 7×Z2 | Z15= Z 5×Z3 | Z16 |
 |  |  |  |  |  |  |  |
| Z17 | Z18= Z 9×Z2 | Z19 | Z20= Z 5×Z4 | Z21= Z 7×Z3 | Z22= Z 11×Z2 | Z23 | Z24= Z 8×Z3 |
 граф Пэли порядка 13, циркулянтный граф, сформированный как граф Кэли of Z / 13 с образующей {1,3,4}
граф Пэли порядка 13, циркулянтный граф, сформированный как граф Кэли of Z / 13 с образующей {1,3,4} A Граф Кэли - это граф, определенный из пары (G, S), где G - группа, а S - множество генераторов для группы; он имеет вершину для каждого элемента группы и ребро для каждого произведения элемента с образующей. В случае конечной циклической группы с ее единственным образующим граф Кэли является графом циклов, а для бесконечной циклической группы с ее образующей граф Кэли является дважды бесконечным графом путей. Однако графы Кэли также могут быть определены из других наборов генераторов. Графы Кэли циклических групп с произвольными образующими называются циркулянтными графами. Эти графы могут быть представлены геометрически как набор равноотстоящих точек на окружности или на линии, каждая точка соединена с соседями с таким же набором расстояний, что и каждая другая точка. Это в точности те вершинно-транзитивные графы, группа симметрии которых включает транзитивную циклическую группу.
Кольцо эндоморфизмов абелевой группы Z/nZизоморфна самому Z/nZкак кольцо. При этом изоморфизме число r соответствует эндоморфизму Z/nZ, который отображает каждый элемент в сумму r его копий. Это биекция тогда и только тогда, когда r взаимно просто с n, поэтому группа автоморфизмов элемента Z/nZизоморфна единичной группе (Z/nZ).
Аналогично, кольцо эндоморфизмов аддитивной группы Z изоморфно кольцу Z . Его группа автоморфизмов изоморфна группе единиц кольца Z, т. Е. ({−1, +1}, ×) ≅ C 2.
Можно показать, что тензорное произведение Z/mZ⊗ Z/nZизоморфно Z / gcd (m, n) Z . Таким образом, мы можем сформировать набор гомоморфизмов группы от Z/mZдо Z/nZ, обозначенных hom (Z/mZ, Z/nZ), которые сами по себе являются группой.
Для тензорного произведения это следствие того общего факта, что R / I ⊗ R R / J ≅ R / (I + J), где R - коммутативное кольцо с единицей, а I и J - идеалы кольца. Напомним, что для группы Hom она изоморфна подгруппе в Z / n Z, состоящей элементов порядка, делящего m. Эта подгруппа cyc lic порядка gcd (m, n), что завершает доказательство.
Несколько других классов групп были определены по их отношению к циклическим группам:
Группа - это называется виртуально циклическим, если он содержит циклическую подгруппу с конечным индексом (количество смежных классов, которые имеет эта подгруппа). Другими словами, любой элемент в фактически циклической группе может быть получен путем применения члена циклической подгруппы к члену в некотором конечном множестве. Каждая циклическая группа практически циклическая, как и любая конечная группа. Бесконечная группа является практически циклической тогда и только тогда, когда она конечно порождена и имеет ровно два конца ; Примером такой группы является прямое произведение из Z/nZи Z, в котором коэффициент Z имеет конечный индекс n. Каждая абелева подгруппа гиперболической группы Громова является практически циклической.
A локально циклическая группа - это группа, в которой каждая конечно порождена подгруппа циклическая. Примером может служить аддитивная группа рациональных чисел : каждый конечный набор рациональных чисел представляет собой набор целых кратных единственной единичной дроби, обратной их наименьшему общему числу. знаменатель, и генерирует как подгруппу циклическую группу целых кратных этой единичной дроби. Группа является локально циклической тогда и только тогда, когда ее решетка подгрупп является дистрибутивной решеткой.
A циклически упорядоченной группой является группой вместе с циклический порядок сохраняется структурой группы. Каждой циклической группе может быть дана структура как циклически упорядоченная группа, согласованная с порядком целых чисел (или целых чисел по модулю порядка группы). Каждая конечная подгруппа циклически упорядоченной группы является циклической.
A метациклическая группа - это группа, содержащая циклическую нормальную подгруппу, фактор которой также является циклическим. Эти группы включают в себя циклические группы, дициклические группы и прямые продукты двух циклических групп. полициклические группы обобщают метациклические группы, допуская более одного уровня расширения группы. Группа является полициклической, если она имеет конечную убывающую последовательность подгрупп, каждая из которых нормальна в предыдущей подгруппе с циклическим фактором, заканчивающимся тривиальной группой. Каждая конечно порожденная абелева группа или нильпотентная группа является полициклической.
Znявляется простым, если n простое.