Векторное пространство

Базовая алгебраическая структура линейной алгебры Сложение векторов и скалярное умножение: вектор v (синий) добавляется к другому вектору w (красный, верхний рисунок). Ниже w растягивается в 2 раза, что дает сумму v + 2 w.

A векторного пространства (также называемого линейным пространством ) представляет собой набор объектов, называемых векторами, которые могут быть сложены вместе и умножены («масштабированы») на числа, называемые скалярами. Скаляры часто считаются действительными числами, но есть также векторные пространства со скалярным умножением на комплексные числа, рациональные числа или вообще любое поле . Операции сложения векторов и скалярного умножения должны удовлетворять определенным требованиям, называемым векторными аксиомами (перечисленными ниже в § Определение). Чтобы указать, что скаляры являются действительными или комплексными числами, часто используются термины вещественное векторное пространство и комплексное векторное пространство .

Определенные наборы евклидовых векторов являются типичными примерами векторного пространства. Они представляют физические величины, такие как силы, где любые две силы (одного типа) могут быть добавлены, чтобы получить третье, и произведение вектора силы по действительному множителю - другой вектор силы. Аналогичным образом (но в более геометрическом смысле) векторы, представляющие смещения в плоскости или трехмерном пространстве, также образуют векторные пространства. Векторы в векторных пространствах не обязательно должны быть объектами в виде стрелок, как они представлены в упомянутых примерах: векторы рассматриваются как абстрактные математические объекты с определенными свойствами, которые в некоторых случаях могут быть визуализированы как стрелки.

Векторные пространства являются предметом линейной алгебры и хорошо характеризуются своей размерностью, которая, грубо говоря, определяет количество независимых направлений в пространстве. Бесконечномерные векторные пространства естественным образом возникают в математическом анализе как функциональные пространства, векторами которых являются функции. Эти векторные пространства обычно наделены некоторой дополнительной структурой, такой как топология , которая позволяет учитывать вопросы близости и непрерывности. Среди этих топологий чаще используются те, которые определены нормой или внутренним продуктом (снабжены понятием расстояния между двумя векторами). Это в особенности случай банаховых пространств и гильбертовых пространств, которые являются фундаментальными в математическом анализе.

Исторически первые идеи, ведущие к векторным пространствам, восходят к аналитической геометрии 17 века, матрицам, системам линейных уравнений и евклидовы векторы. Современный, более абстрактный подход, впервые сформулированный Джузеппе Пеано в 1888 году, охватывает более общие объекты, чем евклидово пространство, но большую часть теории можно рассматривать как расширение классических геометрических идей. например, строки, плоскости и их многомерные аналоги.

Сегодня векторные пространства используются в математике, науке и инженерии. Это подходящее линейно-алгебраическое понятие для работы с системами линейных уравнений. Они предлагают основу для расширения Фурье, которое используется в процедурах сжатия изображений, и они обеспечивают среду, которая может использоваться для методов решения для уравнений в частных производных. Кроме того, векторные пространства предоставляют абстрактный бескординатный способ работы с геометрическими и физическими объектами, такими как тензоры. Это, в свою очередь, позволяет исследовать локальные свойства многообразий методами линеаризации. Векторные пространства можно обобщить несколькими способами, что приведет к более сложным понятиям в геометрии и абстрактной алгебре.

• 1 Введение и определение
  • 1.1 Первый пример: стрелки в плоскости
  • 1.2 Второй пример : упорядоченные пары чисел
  • 1.3 Определение
  • 1.4 Альтернативные формулировки и элементарные последствия
• 2 История
• 3 Примеры
  • 3.1 Координатное пространство
  • 3.2 Комплексные числа и другие расширения полей
  • 3.3 Функция пространства
  • 3.4 Линейные уравнения
• 4 Базис и размерность
• 5 Линейные отображения и матрицы
  • 5.1 Матрицы
  • 5.2 Собственные значения и собственные векторы
• 6 Базовые конструкции
  • 6.1 Подпространства и факторпространства
  • 6.2 Прямое произведение и прямая сумма
  • 6.3 Тензорное произведение
• 7 Векторные пространства с дополнительной структурой
  • 7.1 Нормированные векторные пространства и пространства внутреннего произведения
  • 7.2 Топологические векторные пространства
    • 7.2.1 Банаховы пространства
    • 7.2.2 Гильбертовы пространства
  • 7.3 Алгебры над полями
• 8 Приложения
  • 8.1 Dist Распределения
  • 8.2 Анализ Фурье
  • 8.3 Дифференциальная геометрия
• 9 Обобщения
  • 9.1 Векторные связки
  • 9.2 Модули
  • 9.3 Аффинные и проективные пространства
• 10 См. также
• 11 Примечания
• 12 Цитирования
• 13 Ссылки
  • 13.1 Алгебра
  • 13.2 Анализ
  • 13.3 Исторические ссылки
  • 13.4 Дополнительные ссылки
• 14 Внешние ссылки

Концепция векторного пространства сначала поясняется описанием двух конкретных примеров:

Первый пример: стрелки в плоскости

Первый пример векторного пространства состоит из стрелок в фиксированная плоскость, начиная с одной фиксированной точки. Это используется в физике для описания сил или скоростей. Учитывая любые две такие стрелки, v и w, параллелограмм , охватываемый этими двумя стрелками, также содержит одну диагональную стрелку, которая также начинается в начале координат. Эта новая стрелка называется суммой двух стрелок и обозначается v+ w. В особом случае двух стрелок на одной строке их сумма равна стрелке на этой строке, длина которой равна сумме или разнице длин, в зависимости от того, имеют ли стрелки одинаковое направление. Еще одна операция, которую можно выполнить с помощью стрелок, - это масштабирование: для любого положительного действительного числа a стрелка имеет то же направление, что и v, но расширяется или сужается путем умножения ее длины на a, называется умножением v на a. Обозначается он v . Когда a отрицательно, a v вместо этого определяется как стрелка, указывающая в противоположном направлении.

Ниже показано несколько примеров: если a = 2, результирующий вектор a w имеет то же направление, что и w, но растягивается до двойной длины w (правое изображение ниже). Эквивалентно, 2 w - это сумма w+ w. Кроме того, (-1) v = - v имеет противоположное направление и такую ​​же длину, как v (синий вектор, указывающий вниз на правом изображении).

Второй пример: упорядоченные пары чисел

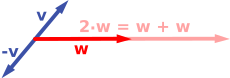Второй ключевой пример векторного пространства представлен парами действительных чисел x и y. (Порядок компонентов x и y имеет значение, поэтому такая пара также называется упорядоченной парой.) Такая пара записывается как (x, y). Сумма двух таких пар и умножение пары на число определяется следующим образом:

$(x\; 1,\; y\; 1)\; +\; (x\; 2,\; y\; 2)\; =\; (x\; 1\; +\; x\; 2,\; y\; 1\; +\; y\; 2)\; \{\backslash \; displaystyle\; (x\_\; \{1\},\; y\_\; \{1\})\; +\; (x\_\; \{2\},\; y\_\; \{2\})\; =\; (x\_\; \{1\}\; +\; x\_\; \{2\},\; y\_\; \{1\}\; +\; y\_\; \{2\})\}$

и

$a\; (x,\; y)\; =\; (ax,\; ay)\; \{\backslash \; displaystyle\; a\; (x,\; y)\; =\; (ax,\; ay)\}$.

Первый пример выше сводится к этому, если стрелки представлены парой декартовых координат их конечных точек.

Определение

В этой статье векторы выделены жирным шрифтом, чтобы отличать их от скаляров.

Векторное пространство над полем F - это задает V вместе с двумя операциями, которые удовлетворяют восьми аксиомам, перечисленным ниже. В дальнейшем V × V обозначает декартово произведение V с самим собой, а → обозначает отображение из одного набора в другой.

• Первая операция, называемая сложение векторов или просто сложение +: V × V → V, принимает любые два вектора v и w и назначает им третий вектор, который обычно записывается как v+ w, и называется суммой этих двух векторов. (Результирующий вектор также является элементом множества V.)
• Вторая операция, называемая скалярным умножением ·: F × V → V ，, принимает любой скаляр a и любого вектора v и дает другому вектору a v . (Точно так же вектор a v является элементом множества V. Скалярное умножение не следует путать со скалярным произведением , также называемым внутренним произведением или скалярным произведением, которое является дополнительная структура присутствует в некоторых конкретных, но не во всех векторных пространствах. Скалярное умножение - это умножение вектора на скаляр; другое - это умножение двух векторов, дающее скаляр.)

Элементы V обычно называют векторами. Элементы F обычно называют скалярами. Общие символы для обозначения векторных пространств включают $U\; \{\backslash \; displaystyle\; U\}$, $V\; \{\backslash \; displaystyle\; V\}$и $W\; \{\backslash \; displaystyle\; W\}$.

В двух приведенных выше примерах поле представляет собой поле действительных чисел, а набор векторов состоит из плоских стрелок с фиксированной начальной точкой и пар действительных чисел соответственно.

Чтобы квалифицироваться как векторное пространство, множество V и операции сложения и умножения должны соответствовать ряду требований, называемых аксиомами. Они перечислены в таблице ниже, где u, vи w обозначают произвольные векторы в V, а a и b обозначают скаляры в F.

Аксиома	Значение
Ассоциативность сложения	u+ (v+ w) = (u+ v) + w
Коммутативность сложения	u+ v= v+ u
Идентификационный элемент сложения	Существует элемент 0 ∈ V, называемый нулевым вектором, такой, что v+ 0= vдля всех v ∈ V.
Обратные элементы сложения	Для каждого v ∈ V существует элемент - v ∈ V, называемый аддитивным обратным для v, такое, что v + (- v ) = 0.
Совместимость скалярного умножения с полевым умножением	a (b v ) = (ab) v
Элемент идентичности скалярного умножения	1v= v, где 1 обозначает мультипликативную идентичность в F.
Дистрибутивность скалярного умножения по отношению к сложению векторов	a(u+ v) = a u + a v
Дистрибутивность скалярного умножения по сложение полей	(a + b) v = a v + b v

Эти аксиомы обобщают свойства векторов, представленных в приведенных выше примерах. Действительно, результат сложения двух упорядоченных пар (как во втором примере выше) не зависит от порядка слагаемых:

(xv, y v) + (x w, y w) = (x w, y w) + (x v, y v).

Аналогично, в геометрическом примере векторов в виде стрелок, v+ w= w+ v, поскольку параллелограмм, определяющий сумму векторов, не зависит от порядка векторов. Все остальные аксиомы могут быть проверены аналогичным образом в обоих примерах. Таким образом, игнорируя конкретную природу конкретного типа векторов, определение объединяет эти два и многие другие примеры в одно понятие векторного пространства.

Вычитание двух векторов и деление на (ненулевой) скаляр можно определить как

$v\; -\; w\; =\; v\; +\; (-\; w)\; va\; =\; 1\; av\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; mathbf\; \{v\}\; -\; \backslash \; mathbf\; \{w\}\; =\; \backslash \; mathbf\; \{v\}\; +\; (-\; \backslash \; mathbf\; \{w\})\; \backslash \backslash \; \{\backslash \; frac\; \{\backslash \; mathbf\; \{v\}\}\; \{a\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{\; a\}\}\; \backslash \; mathbf\; \{v\}\; \backslash \; end\; \{align\}\}\}$.

Когда скалярное поле F представляет собой действительные числа R, векторное пространство называется вещественным вектором sp туз. Когда скалярное поле представляет собой комплексные числа C, векторное пространство называется комплексным векторным пространством. Эти два случая чаще всего используются в инженерии. Общее определение векторного пространства позволяет скалярам быть элементами любого фиксированного поля F. Это понятие тогда известно как F-векторное пространство или векторное пространство над F. Поле, по сути, представляет собой набор чисел, обладающих сложением, вычитанием, умножением и деление операций. Например, рациональные числа образуют поле.

В отличие от интуиции, проистекающей из векторов в плоскости и многомерных случаев, в общих векторных пространствах нет понятия близости, углов или расстояния. Чтобы иметь дело с такими вопросами, вводятся определенные типы векторных пространств; см. § Векторные пространства с дополнительной структурой ниже для получения дополнительной информации.

Альтернативные формулировки и элементарные следствия

Сложение векторов и скалярное умножение - это операции, удовлетворяющие свойству замыкания : u+ vи v находятся в V для всех a в F и u, vв V. Некоторые старые источники упоминают эти свойства как отдельные аксиомы.

На языке абстрактной алгебры первые четыре аксиомы эквивалентны требуя, чтобы набор векторов был абелевой группой при добавлении. Остальные аксиомы придают этой группе структуру F- module. Другими словами, существует кольцевой гомоморфизм f из поля F в кольцо эндоморфизмов группы векторов. Тогда скалярное умножение a v определяется как (f (a)) (v).

Аксиомы векторного пространства имеют ряд прямых следствий. Некоторые из них вытекают из теории элементарных групп, применяемый к аддитивной группе векторов: например, нулевой вектор 0 вектора V и аддитивный обратный - v любого вектора v уникальны. Дальнейшие свойства следуют с использованием также закона распределения для скалярного умножения, например, a v равно 0 тогда и только тогда, когда a равно 0 или v равно 0.

Векторные пространства произошли от аффинной геометрии посредством введения координат в плоском или трехмерном пространстве. Около 1636 года французские математики Рене Декарт и Пьер де Ферма основали аналитическуюгеометрию, определив решения уравнения двух переменных с точками на плоскости кривой. Получить геометрические решения без используя координаты, Больцано представил, в 1804 году определенные операции с точками, линиями и плоскостями, которые являются предшественниками векторов. Эта работа была использована в концепции барицентрических координат Мёбиуса в 1827 году. Основой определения векторов было понятие Беллавитиса о двойной точке, ориентированный сегмент, один из концов которого является исходной точкой, а другой - целью. Векторы были пересмотрены с представлением комплексных чисел Арганом и Гамильтоном и созданием кватернионов последним. Они являются элементами в R и R ; Обработка их с помощью линейных комбинаций восходит к Лагеру в 1867 году, который также определил системы линейных уравнений.

В 1857 году Кэли ввел матричная запись, которая позволяет согласовывать и упрощать линейные карты. Примерно в то же время Грассман изучил барицентрическое исчисление, начатое Мёбиусом. Он представлял себе наборы абстрактных объектов, наделенных операциями. В его работе присутствуют понятия линейной независимости и размерности, а также скалярных произведений. На самом деле работы Грассмана 1844 года выходят за рамки векторных пространств, поскольку его размышления об умножении тоже привели его к тому, что сегодня называют алгебрами. Итальянский математик Пеано был первым, кто дал современное определение векторных пространств и линейных отображений в 1888 году.

Важное развитие векторных пространств связано с построением функциональных пространств автора Анри Лебег. Позднее это было формализовано Банахом и Гильбертом, примерно в 1920 году. В то время алгебра и новая область функционального анализа начали взаимодействуют, в частности, с ключевыми понятиями, такими как пространства p-интегрируемых функций и гильбертовы пространства. Также в это время были выполнены первые исследования бесконечномерных векторных пространств.

Координатное пространство

Простейшим примером векторного пространства над полем F является само поле, снабженное его стандартным сложением и умножением. В более общем смысле, все n-кортежи (последовательности длины n)

(a1, 2,..., n)

элементов F образуют векторное пространство, которое обычно обозначается F и называется координатным пространством . Случай n = 1 представляет собой упомянутый выше простейший пример, в котором поле F также рассматривается как векторное пространство над собой. Случай F = R и n = 2 обсуждался во введении выше.

Комплексные числа и другие расширения полей

Набор комплексных чисел C, то есть чисел, которые могут быть записаны в форме x + iy для действительных чисел x и y, где i - мнимая единица, образуют векторное пространство над вещественными числами с помощью обычного сложения и умножения: (x + iy) + (a + ib) = (x + a) + i (y + b) и c ⋅ (x + iy) = (c ⋅ x) + i (c ⋅ y) для действительных чисел x, y, a, b и c. Различные аксиомы векторного пространства вытекают из того факта, что одни и те же правила выполняются для арифметики комплексных чисел.

Фактически, пример комплексных чисел по сути такой же (то есть он изоморфен) упомянутому выше векторному пространству упорядоченных пар действительных чисел: если мы думаем о комплексном числе x + iy как представляя упорядоченную пару (x, y) на комплексной плоскости , то мы видим, что правила сложения и скалярного умножения точно соответствуют тем, что в предыдущем примере.

В более общем плане расширения поля предоставляют другой класс примеров векторных пространств, особенно в алгебре и теории алгебраических чисел : поле F, содержащее меньшее поле E является E-векторным пространством, посредством заданных операций умножения и сложения F. Например, комплексные числа представляют собой векторное пространство над R, а расширение поля $Q\; (i\; 5)\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{Q\}\; (i\; \{\backslash \; sqrt\; \{5\}\})\}$- векторное пространство над Q.

функциональными пространствами

Сложение функций: сумма синуса и экспоненциальная функция: $sin\; +\; exp:\; R\; \to \; R\; \{\backslash \; displaystyle\; \backslash \; sin\; +\; \backslash \; exp:\; \backslash \; mathbb\; \{R\}\; \backslash \; to\; \backslash \; mathbb\; \{R\}\}$с $(sin\; +\; exp)\; (Икс)\; знак\; равно\; грех\; \; (Икс)\; +\; ехр\; \; (Икс)\; \{\backslash \; Displaystyle\; (\backslash \; sin\; +\; \backslash \; exp)\; (x)\; =\; \backslash \; sin\; (x)\; +\; \backslash \; exp\; (x)\}$

Функции из любого фиксированного набора Ω к полю F также образуют векторные пространства, выполняя точечное сложение и скалярное умножение. То есть сумма двух функций f и g - это функция (f + g), заданная как

(f + g) (w) = f (w) + g (w),

и аналогично для умножения. Такиефункциональные пространства встречаются во многих геометрических ситуациях, когда Ω является вещественной линией или интервалом, или другими подмножествами из R . Многие понятия в топологии и анализе, такие как непрерывность, интегрируемость или дифференцируемость, хорошо подходят для линейности: суммы и скалярные кратные функции, обладающие таким собственность все еще имеет это свойство. Следовательно, набор таких функций - векторные пространства. Более подробно они изучаются с использованием методов функционального анализа, см. ниже. Алгебраические ограничения также порождают векторные пространства: векторное пространство F [x] задается полиномиальными функциями :

f (x) = r 0 + r 1 x +... + r n − 1 x + r n x, где коэффициенты r0,..., r n находятся в F.

Линейные уравнения

Системы однородных линейных уравнений тесно связаны с векторными пространствами. Например, решения

a	+	3b	+	c	= 0
4a	+	2b	+	2c	= 0

задаются тройками с произвольными a, b = a / 2 и c = −5a / 2. Они образуют векторное пространство: суммы и скалярные кратные таких троек по-прежнему удовлетворяют тем же отношениям трех переменных; таким образом, они тоже являются решениями. Матрицы могут использоваться для сжатия нескольких линейных уравнений, как указано выше, в одно векторное уравнение, а именно

Ax= 0,

, где A = $[1\; 3\; 1\; 4\; 2\; 2]\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{bmatrix\}\; 1\; 3\; 1\; \backslash \backslash \; 4\; 2\; 2\; \backslash \; end\; \{bmatrix\}\}\}$- это матрица, содержащая коэффициенты данных уравнений, x - вектор (a, b, c), A x обозначает матричное произведение, а 0 = (0, 0) - нулевой вектор. Аналогичным образом решения однородных линейных дифференциальных уравнений образуют векторные пространства. Например,

f ′ ′ (x) + 2f ′ (x) + f (x) = 0

дает f (x) = ae + bx e, где a и b - произвольные константы, а e - естественная экспоненциальная функция.

Вектор v в R (синий), выраженный в различных основаниях: с использованием стандартного базиса из Rv= x e1+ y e2(черный), и с использованием другого, не ортогонального базиса: v= f1+ f2(красный).

Базы позволяют для представления векторов последовательностью скаляров, называемых координатами или компонентами. Базис - это (конечный или бесконечный) набор B = {bi}i ∈ I векторов bi, для удобства часто индексируемый некоторым набором индексов I, который охватывает все пространство и линейно независимый. «Охват всего пространства» означает, что любой вектор v может быть выражен как конечная сумма (называемая линейной комбинацией ) базовых элементов:

$v\; =\; a\; 1\; bi\; 1\; +\; a\; 2\; bi\; 2\; +\; \cdots \; +\; anbin,\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{v\}\; =\; a\_\; \{1\}\; \backslash \; mathbf\; \{b\}\; \_\; \{i\_\; \{1\}\}\; +\; a\_\; \{2\}\; \backslash \; mathbf\; \{b\}\; \_\; \{i\_\; \{2\; \}\}\; +\; \backslash \; cdots\; +\; a\_\; \{n\}\; \backslash \; mathbf\; \{b\}\; \_\; \{i\_\; \{n\}\},\}$

(1)

где a k - скаляры, называемые координатами (или компонентами) вектор v относительно базиса B и bik(k = 1,..., n) элементов B. Линейная независимость означает, что координаты a k однозначно определяется для любого вектора в векторном пространстве.

Например, векторы координат e1= (1, 0,..., 0), e2= (0, 1, 0,..., 0), чтобы en= (0, 0,..., 0, 1), образуют основу F, называемую стандартным базисом, поскольку любой вектор (x 1, x 2,..., x n) могут быть однозначно выражены как линейная комбинация этих векторов:

(x1, x 2,..., x n) = x 1 (1, 0,..., 0) + x 2 (0, 1, 0,..., 0) +... + x n (0,..., 0, 1) = x 1e1+ x 2e2+... + x nen.

Соответствующие координаты x 1, x 2,..., x n - это просто декартовы координаты вектора.

Каждое векторное пространство имеет основу. Это следует из леммы Цорна, эквивалентной формулировке Аксиомы выбора. Учитывая другие аксиомы теории множеств Цермело – Френкеля, существование базисов эквивалентно аксиоме выбора. Лемма об ультрафильтрации, которая слабее выбранной аксиомы, подразумевает, что все базы данного векторного пространства имеют одинаковое количество элементов или мощность (см. Dimension теорема для векторных пространств ). Он называется размерностью векторного пространства и обозначается dim V. Если пространство покрыто конечным числом векторов, приведенные выше утверждения могут быть доказаны без такого фундаментального вклада теории множеств.

Размерность координаты пространство F равно n в соответствии с изложенным выше основанием. Размерность кольца многочленов F [x], введенного выше, равна счетно бесконечной, базис задается 1, x, x,... Тем более, размерность более общих функциональных пространств, таких как пространство функций на некотором (ограниченном или неограниченном) интервале, бесконечна. При подходящих предположениях регулярности участвующих коэффициентов размерность пространства решений однородного обыкновенного дифференциального уравнения равна степени уравнения. Например, пространство решений для приведенного выше уравнения генерируется e и xe. Эти две функции линейно независимы в пределах R, поэтому размерность этого пространства равна двум, как и степень уравнения.

Расширение поля над рациональными числами Q можно рассматривать как векторное пространство над Q (путем определения сложения векторов как сложения полей, определения скалярного умножения как умножения полей на элементы Q, и в противном случае игнорируя умножение полей). Размер (или градусов ) расширения поля Q (α) над Q зависит от α. Если α удовлетворяет некоторому полиномиальному уравнению

$qn\; \alpha \; n\; +\; qn\; -\; 1\; \alpha \; n\; -\; 1\; +\; \cdots \; +\; q\; 0\; =\; 0\; \{\backslash \; displaystyle\; q\_\; \{n\}\; \backslash \; alpha\; ^\; \{n\}\; +\; q\_\; \{n-1\}\; \backslash \; alpha\; ^\; \{n-1\}\; +\; \backslash \; cdots\; +\; q\_\; \{0\}\; =\; 0\}$с рациональными коэффициентами q n,..., q 0 (другими словами, если α алгебраический ) размерность конечна. Точнее, он равен степени минимального многочлена , имеющего α в качестве корня . Например, комплексные числа C представляют собой двумерное вещественное векторное пространство, генерируемое 1 и мнимой единицей i. Последний удовлетворяет i + 1 = 0, уравнению второй степени. Таким образом, C является двумерным векторным пространством R (и, как любое поле, одномерным как векторное пространство над собой, C ). Если α не является алгебраическим, размерность Q (α) над Q бесконечна. Например, для α = π такого уравнения нет, другими словами, π является трансцендентным.

Связь двух векторов пространства могут быть выражены линейной картой или линейным преобразованием. Это функции, которые отражают структуру векторного пространства, то есть они сохраняют суммы и скалярное умножение:

$f\; (v\; +\; w)\; =\; f\; (v)\; +\; f\; (w)\; \{\backslash \; displaystyle\; f\; (\; \backslash \; mathbf\; \{v\}\; +\; \backslash \; mathbf\; \{w\})\; =\; f\; (\backslash \; mathbf\; \{v\})\; +\; f\; (\backslash \; mathbf\; \{w\})\}$и f (a · v) $=\; \{\backslash \; displaystyle\; =\; \}$a · f (v ) для всех v и w в V, все a в F.

An изоморфизм - это линейное отображение f: V → W такое, что существует обратное отображение g: W → V, которое является отображением такое, что две возможные композиции f ∘ g: W → W и g ∘ f: V → V являются тождественными отображениями. Эквивалентно, f взаимно однозначно (инъективно ) и на (сюръективно ). Если существует изоморфизм между V и W, эти два пространства называются изоморфными; тогда они по существу идентичны как векторные пространства, так как все тождества, сохраняющиеся в V, через f переносятся в аналогичные в W, и наоборот через g.

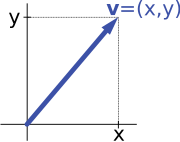Описание вектора стрелки v его координатами x и y приводит к изоморфизму векторных пространств.

Например, векторные пространства «стрелки на плоскости» и «упорядоченные пары чисел» во введении изоморфны: плоская стрелка v, исходящая из origin некоторой (фиксированной) системы координат может быть выражено как упорядоченная пара, учитывая x- и y-компоненты стрелки, как показано на изображении справа. И наоборот, если дана пара (x, y), стрелка, идущая по x вправо (или влево, если x отрицательно), и y вверх (вниз, если y отрицательно) поворачивает стрелку назад v.

Линейный отображает V → W между двумя векторными пространствами, образуя векторное пространство Hom F (V, W), также обозначаемое L (V, W). Пространство линейных отображений из V в F называется двойным векторным пространством, обозначается V. С помощью инъективного естественного отображения V → V любое векторное пространство может быть вложено в его двузначное; отображение является изоморфизмом тогда и только тогда, когда пространство конечномерно.

После выбора базиса V линейные отображения f: V → W полностью определяются путем задания образов базисных векторов, потому что любой элемент V однозначно выражается как их линейная комбинация. Если dim V = dim W, однозначное соответствие между фиксированными базами V и W приводит к линейному отображению, которое отображает любой базисный элемент V в соответствующий базовый элемент W. Это изоморфизм по самому его определению. Следовательно, два векторных пространства изоморфны, если их размерности совпадают, и наоборот. Другой способ выразить это: любое векторное пространство полностью классифицируется (от до изоморфизма) по своей размерности, одному числу. В частности, любое n-мерное F-векторное пространство V изоморфно F. Однако не существует«канонического» или предпочтительного изоморфизма; на самом деле изоморфизм φ: F → V эквивалентен выбору базиса V путем отображения стандартного базиса F в V через φ. Свобода выбора удобной основы особенно полезна в бесконечномерном контексте; см. ниже.

Матрицы

Типичная матрица

Матрицы - полезное понятие для кодирования линейных карт. Они записаны в виде прямоугольного массива скаляров, как на изображении справа. Любая матрица A размером m x n приводит к линейному отображению из F в F следующим образом:

$x\; =\; (x\; 1,\; x\; 2,\dots ,\; xn)\; \mapsto \; (\sum \; j\; =\; 1\; na\; 1\; jxj,\; \sum \; j\; Знак\; равно\; 1\; na\; 2\; jxj,\dots ,\; \sum \; j\; =\; 1\; namjxj)\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{x\}\; =\; (x\_\; \{1\},\; x\_\; \{2\},\; \backslash \; ldots,\; x\_\; \{n\})\; \backslash \; mapsto\; \backslash \; left\; (\backslash \; sum\; \_\; \{j\; =\; 1\}\; ^\; \{n\}\; a\_\; \{1j\}\; x\_\; \{j\},\; \backslash \; sum\; \_\; \{j\; =\; 1\}\; ^\; \{n\}\; a\_\; \{2j\}\; x\_\; \{j\},\; \backslash \; ldots,\; \backslash \; sum\; \_\; \{j\; =\; 1\}\; ^\; \{n\}\; a\_\; \{mj\}\; x\_\; \{j\}\; \backslash \; right)\}$, где $\sum \; \{\backslash \; displaystyle\; \backslash \; sum\}$обозначает суммирование,

или, с использованием матричного умножения матрицы A на вектор координат x:

x↦ A x.

Более того, после выбора базисов V и W любая линейная карта f: V → W однозначно представлена ​​матрицей посредством этого присваивания.

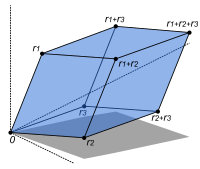Объем этого параллелепипеда является абсолютным значением определителя матрицы 3 на 3, образованной векторами r 1, r 2 и r 3.

Определитель det (A) квадратной матрицы A - это скаляр, который сообщает, является ли связанная карта изоморфизмом или нет: быть так что достаточно и не Очевидно, что определитель отличен от нуля. Линейное преобразование R, соответствующее вещественной матрице размера n на n, является с сохранением ориентации тогда и только тогда, когда его определитель положительный.

Собственные значения и собственные векторы

Эндоморфизмы, линейные отображения f: V → V, особенно важны, поскольку в этом случае векторы v можно сравнивать с их изображением при f, f (v ). Любой ненулевой вектор v, удовлетворяющий λ v = f (v ), где λ - скаляр, называется собственным вектором f с собственным значением λ. Эквивалентно, v является элементом ядра разности f - λ · Id (где Id - идентификационная карта V → V). Если V конечномерно, это можно перефразировать с помощью определителей: f, имеющее собственное значение λ, эквивалентно

det (f - λ · Id) = 0.

Если описать определение определителя, выражение на левая часть может рассматриваться как полиномиальная функция от λ, называемая характеристическим полиномом функции f. Если поле F достаточно велико, чтобы содержать ноль этого многочлена (что автоматически происходит для F алгебраически замкнутого, такого как F = C ), любая линейная карта имеет по крайней мере один собственный вектор. Векторное пространство V может иметь или не иметь собственный базис, базис, состоящий из собственных векторов. Это явление регулируется Иорданской канонической формой карты. Набор всех собственных векторов, соответствующих конкретному собственному значению f, образует векторное пространство, известное как собственное подпространство, соответствующее собственному значению (и f), о котором идет речь. Для достижения спектральной теоремы, соответствующего утверждения в бесконечномерном случае, необходим аппарат функционального анализа, см. ниже.

В дополнение к над конкретными примерами существует ряд стандартных линейных алгебраических конструкций, которые дают векторные пространства, связанные с заданными. В дополнение к определениям, данным ниже, они также характеризуются универсальными свойствами, которые определяют объект X путем задания линейных отображений из X в любое другое векторное пространство.

Подпространства и частные пространства

Линия, проходящая через начало координат (синяя, толстая) в R, является линейным подпространством. Это пересечение двух плоскостей (зеленой и желтой).

Непустое подмножество W векторного пространства V, которое замкнуто при сложении и скалярном умножении (и поэтому содержит 0 -вектор V) называется линейным подпространством V или просто подпространством V, когда объемлющее пространство однозначно является векторным пространством. Подпространства V являются векторными пространствами (над одним и тем же полем) сами по себе. Пересечение всех подпространств, содержащих данный набор векторов S, называется его промежутком, и это наименьшее подпространство V, содержащее множество S. Выраженное в терминах элементов, промежуток - это подпространство, состоящее из всех линейные комбинации элементов S.

Линейное подпространство размерности 1 представляет собой векторную линию . Линейное подпространство размерности 2 - это векторная плоскость . Линейное подпространство, которое содержит все элементы, кроме одного из базиса окружающего пространства, представляет собой векторную гиперплоскость . В векторном пространстве конечной размерности n векторная гиперплоскость, таким образом, является подпространством размерности n - 1.

Аналог подпространств - факторные векторные пространства. Для любого подпространства W ⊂ V фактор-пространство V / W («V по модулю W») определяется следующим образом: как множество оно состоит из v + W = {v+ w: w∈ W}, где v - произвольный вектор из V. Сумма двух таких элементов v1+ W и v2+ W равна (v1+ v2) + W, и скалярное умножение дается выражением a · (v + W) = (a · v ) + W. Ключевым моментом в этом определении является то, что v1+ W = v2+ W тогда и только тогда, когда разница между v1и v2лежит в W. Таким образом, факторное пространство "забывает" информацию, содержащуюся в подпространстве W.

ядро ​​ ker (f) линейного отображения f: V → W состоит из векторов v, которые отображаются в 0 в W. Ядро и image im (f) = {f (v ): v ∈ V} являются подпространствами V и W соответственно. Существование ядер и изображений является частью утверждения, что категория векторных пространств (над фиксированным полем F) является абелевой категорией, то есть корпусом математических объектов и сохраняющие структуру карты между ними (категория ), которые ведут себя так же, как категория абелевых групп. Из-за этого многие утверждения, такие как первая теорема об изоморфизме (также называемая теоремой о нулевом ранге в терминах, связанных с матрицами)

V / ker (f) ≡ im (f

, а вторая и третья теоремы об изоморфизме могут быть сформулированы и доказаны способом, очень похожим на соответствующие утверждения для групп.

Важным примером является ядро ​​линейного отображения x ↦ A x для некоторой фиксированной матрицы A, как выше. Ядром этого отображения является подпространство векторов x таких, что A x = 0, что в точности является набором решений системы однородных линейных уравнений, принадлежащих A. Это понятие также распространяется на линейные дифференциальные уравнения

$a\; 0\; f\; +\; a\; 1\; dfdx\; +\; a\; 2\; d\; 2\; fdx\; 2\; +\; \cdots \; +\; andnfdxn\; =\; 0\; \{\backslash \; displaystyle\; a\_\; \{0\}\; f\; +\; a\_\; \{1\}\; \{\backslash \; frac\; \{df\}\; \{dx\; \}\}\; +\; a\_\; \{2\}\; \{\backslash \; frac\; \{d\; ^\; \{2\}\; f\}\; \{dx\; ^\; \{2\}\}\}\; +\; \backslash \; cdots\; +\; a\_\; \{n\}\; \{\backslash \; frac\; \{d\; ^\; \{n\}\; f\}\; \{dx\; ^\; \{n\; \}\}\}\; =\; 0\}$, где коэффициенты a i также являются функциями от x.

В соответствующая карта

$f\; \mapsto \; D\; (f)\; =\; \sum \; i\; =\; 0\; naidifdxi\; \{\backslash \; displaystyle\; f\; \backslash \; mapsto\; D\; (f)\; =\; \backslash \; sum\; \_\; \{i\; =\; 0\}\; ^\; \{n\}\; a\_\; \{i\}\; \{\backslash \; frac\; \{d\; ^\; \{i\}\; f\}\; \{dx\; ^\; \{i\}\}\}\}$,

производные функции f появляются линейно (в отличие от f ′ ′ (x), например). Поскольку дифференцирование является линейной процедурой (то есть (f + g) ′ = f ′ + g ′ и (c · f) ′ = c · f ′ для константы c), это присвоение является линейным и называется linear дифференциальный оператор. В частности, решения дифференциального уравнения D (f) = 0 образуют векторное пространство (над R или C ).

Прямое произведение и прямая сумма

Прямое произведение векторных пространств и прямая сумма векторных пространств - это два способа объединения индексированного семейства векторных пространств в новое векторное пространство.

Прямое произведение $\prod \; i\; \in \; IV\; i\; \{\backslash \; displaystyle\; \backslash \; textstyle\; \{\backslash \; prod\; \_\; \{i\; \backslash \; in\; I\}\; V\_\; \{i\}\}\}$семейства векторных пространств V i состоит из набора всех кортежей (vi)i ∈ I, которые определяют для каждого индекса i в некотором наборе индексов I элемент viиз V i. Сложение и скалярное умножение выполняется покомпонентно. Вариант этой конструкции - прямая сумма $\oplus \; i\; \in \; IV\; i\; \{\backslash \; displaystyle\; \backslash \; oplus\; \_\; \{i\; \backslash \; in\; I\}\; V\_\; \{i\}\}$(также называется сопродуктом и обозначается $\coprod \; i\; \in \; IV\; i\; \{\backslash \; displaystyle\; \backslash \; textstyle\; \{\backslash \; coprod\; \_\; \{i\; \backslash \; in\; I\}\; V\_\; \{i\}\}\}$), где разрешены только кортежи с конечным числом ненулевых векторов. Если набор индексов I конечен, две конструкции согласуются, но в целом они различны.

Тензорное произведение

Тензорное произведение V ⊗ F W, или просто V ⊗ W, двух векторных пространств V и W является одним из центральных понятий полилинейной алгебры, которая имеет дело с расширяющими понятиями, такими как линейная сопоставляется с несколькими v доступные. Отображение g: V × W → X называется билинейным, если g линейно по обеим переменным v и w . То есть для фиксированного w отображение v ↦ g (v, w) линейно в указанном выше смысле, а также для фиксированного v.

тензорное произведение - это конкретный вектор пространство, которое является универсальным получателем билинейных отображений g, следующим образом. Оно определяется как векторное пространство, состоящее из конечных(формальных) сумм символов, называемых тензорами

v1⊗ w1+ v2⊗ w2+... + vn⊗ wn,

, в соответствии с правилами

a · (v⊗ w) = (a · v ) ⊗ w= v⊗ (a · w ), где a - скаляр,

(v1+ v2) ⊗ w= v1⊗ w+ v2⊗ wи

v⊗ (w1+ w2) = v⊗ w1+ v⊗ w2.

Коммутативная диаграмма, изображающая универсальное свойство тензорного произведения.

Эти правила гарантируют, что отображение f из V × W в V ⊗ W, которое отображает кортеж (v, w) в v⊗ wявляется билинейным. Универсальность утверждает, что для любого векторного пространства X и любого билинейного отображения g: V × W → X существует единственное отображение u, показанное на диаграмме пунктирной стрелкой, композиция с f равным g: u (v⊗ w) = g (v, w). Это называется универсальным свойством тензорного произведения, экземпляром метода - часто используемого в продвинутой абстрактной алгебре - для косвенного определения объектов путем указания карт из этого объекта или в этот объект.

С точки зрения линейной алгебры, векторные пространства полностью понимаются, поскольку любое векторное пространство с точностью до изоморфизма характеризуется своей размерностью. Однако векторные пространства сами по себе не предлагают основы для решения вопроса, который имеет решающее значение для анализа, сходится ли последовательность функций к другой функции. Точно так же линейная алгебра не приспособлена для работы с бесконечной серией, поскольку операция сложения позволяет добавлять только конечное число членов. Следовательно, потребности функционального анализа требуют рассмотрения дополнительных структур.

В векторном пространстве может быть задан частичный порядок ≤, при котором можно сравнивать некоторые векторы. Например, n-мерное реальное пространство R можно упорядочить, сравнивая его векторы покомпонентно. Упорядоченные векторные пространства, например пространства Рисса, являются фундаментальными для интегрирования Лебега, которое основывается на возможности выразить функцию как разность двух положительных функций

f = f - f,

где f обозначает положительную часть f, а f отрицательную часть.

Нормированные векторные пространства и пространства внутренних произведений

"Измерение" векторов выполнено путем указания norm, элемента данных, который измеряет длину векторов, или внутреннего произведения, которое измеряет углы между векторами. Обозначены нормы и внутренние продукты $|\; v\; |\; \{\backslash \; displaystyle\; |\; \backslash \; mathbf\; \{v\}\; |\}$и $⟨v,\; w⟩\; \{\backslash \; displaystyle\; \backslash \; langle\; \backslash \; mathbf\; \{v\},\; \backslash \; mathbf\; \{w\}\; \backslash \; rangle\}$соответственно. Из данных внутреннего продукта следует, что длины векторов также могут быть определены путем определения связанной нормы $|\; v\; |\; :\; =\; ⟨V,\; v⟩\; \{\backslash \; displaystyle\; |\; \backslash \; mathbf\; \{v\}\; |:\; =\; \{\backslash \; sqrt\; \{\backslash \; langle\; \backslash \; mathbf\; \{v\},\; \backslash \; mathbf\; \{v\}\; \backslash \; rangle\}\}\}$. Векторные пространства, снабженные такими данными, называются нормированными векторными пространствами и пространствами внутреннего произведения соответственно.

Координатное пространство F может быть оснащено стандартным скалярным произведением :

$⟨x,\; y⟩\; =\; x\; \cdot \; у\; знак\; равно\; х\; 1\; у\; 1\; +\; \cdots \; +\; xnyn.\; \{\backslash \; displaystyle\; \backslash \; langle\; \backslash \; mathbf\; \{x\},\; \backslash \; mathbf\; \{y\}\; \backslash \; rangle\; =\; \backslash \; mathbf\; \{x\}\; \backslash \; cdot\; \backslash \; mathbf\; \{y\}\; =\; x\_\; \{1\}\; y\_\; \{1\}\; +\; \backslash \; cdots\; +\; x\_\; \{n\}\; y\_\; \{\; n\}.\}$

В R это отражает общее понятие угла между двумя векторами x и y согласно закону косинусы :

$x\; \cdot \; y\; =\; cos\; \; (\angle \; (x,\; y))\; \cdot \; |\; х\; |\; \cdot \; |\; y\; |.\; \{\backslash \; Displaystyle\; \backslash \; mathbf\; \{x\}\; \backslash \; cdot\; \backslash \; mathbf\; \{y\}\; =\; \backslash \; cos\; \backslash \; left\; (\backslash \; angle\; (\backslash \; mathbf\; \{x\},\; \backslash \; mathbf\; \{y\})\; \backslash \; right)\; \backslash \; cdot\; |\; \backslash \; mathbf\; \{x\}\; |\; \backslash \; cdot\; |\; \backslash \; mathbf\; \{y\}\; |.\}$

Из-за этого два вектора, удовлетворяющие $⟨x,\; y⟩\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; langle\; \backslash \; mathbf\; \{x\},\; \backslash \; mathbf\; \{y\}\; \backslash \; rangle\; =\; 0\}$называются ортогональными. Важный вариант стандартного скалярного произведения используется в пространстве Минковского : R, наделенном произведением Лоренца

$⟨x\; |\; Y⟩\; знак\; равно\; Икс\; 1\; Y\; 1\; +\; Икс\; 2\; Y\; 2\; +\; Икс\; 3\; Y\; 3\; -\; Икс\; 4\; Y\; 4.\; \{\backslash \; displaystyle\; \backslash \; langle\; \backslash \; mathbf\; \{x\}\; |\; \backslash \; mathbf\; \{y\}\; \backslash \; rangle\; =\; x\_\; \{1\}\; y\_\; \{1\}\; +\; x\_\; \{2\}\; y\_\; \{2\}\; +\; x\_\; \{3\}\; y\_\; \{3\}\; -x\_\; \{4\}\; y\_\; \{4\}.\}$

В отличие от стандартного скалярного произведения, это не положительно определенное : $⟨x\; |\; x⟩\; \{\backslash \; displaystyle\; \backslash \; langle\; \backslash \; mathbf\; \{x\}\; |\; \backslash \; mathbf\; \{x\}\; \backslash \; rangle\}$также принимает отрицательные значения, например для $x\; =\; (0,\; 0,\; 0,\; 1)\; \{\; \backslash \; Displaystyle\; \backslash \; mathbf\; \{x\}\; =\; (0,0,0,1)\}$. Выделение четвертой координаты - , соответствующей времени, в отличие от трех пространственных измерений - делает ее полезной для математической обработки специальной теории относительности.

Топологические векторные пространства

Конвергенция вопросы решаются путем рассмотрения векторных пространств V, несущих совместимую топологию , структуру, которая позволяетговорить об элементах, близких друг к другу. Совместимость здесь означает, что сложение и скалярное умножение должны быть непрерывными отображениями. Грубо говоря, если x и y в V и a в F изменяются на ограниченную величину, то также изменяются x+ yи x . Чтобы иметь смысл определять величину изменения скаляра, поле F также должно нести топологию в этом контексте; обычно выбирают действительные или комплексные числа.

В таких топологических векторных пространствах можно рассматривать серии векторов. бесконечная сумма

$\sum \; i\; =\; 0\; \infty \; fi\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{i\; =\; 0\}\; ^\; \{\backslash \; infty\}\; f\_\; \{i\}\}$

обозначает предел соответствующие конечные частичные суммы последовательности (f i)i∈Nэлементов V. Например, f i могут быть (действительными или комплексными) функциями, принадлежащими некоторому функциональному пространству V, в этом случае ряд является функциональным рядом. Режим сходимости ряда зависит от топологии, наложенной на функциональное пространство. В таких случаях поточечная сходимость и равномерная сходимость - два ярких примера.

Единичные «сферы» в R состоят из плоских векторов нормы 1. Изображены единичные сферы в различных p-norm, для p = 1, 2 и ∞. Большим ромбиком обозначены точки 1-нормы, равной 2.

Способ убедиться в существовании пределов некоторой бесконечной серии - это ограничить внимание в пространства, где любая последовательность Коши имеет предел; такое векторное пространство называется полным. Грубо говоря, векто r пространство заполнено при условии, что оно содержит все необходимые ограничения. Например, векторное пространство многочленов на единичном интервале [0,1], снабженное топологией равномерной сходимости, не является полным, потому что любая непрерывная функция на [0,1] может быть равномерно аппроксимирована последовательность полиномов по аппроксимационной теореме Вейерштрасса. Напротив, пространство всех непрерывных функций на [0,1] с той же топологией полно. Норма порождает топологию, определяя, что последовательность векторов vnсходится к v тогда и только тогда, когда

$lim\; n\; \to \; \infty \; |\; v\; n\; -\; v\; |\; =\; 0.\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{lim\}\}\; \_\; \{n\; \backslash \; rightarrow\; \backslash \; infty\}\; |\; \backslash \; mathbf\; \{v\}\; \_\; \{n\}\; -\; \backslash \; mathbf\; \{v\}\; |\; =\; 0.\}$

Банаховы и гильбертовы пространства полные топологические векторные пространства, топологии которых задаются, соответственно, нормой и внутренним произведением. Их исследование - ключевой элемент функционального анализа - сосредоточено на бесконечномерных векторных пространствах, поскольку все нормы конечномерных топологических векторных пространств порождают одно и то же понятие сходимости. Изображение справа показывает эквивалентность 1-нормы и ∞-нормы на R : поскольку единичные "шары" окружают друг друга, последовательность сходится к нулю в одной норме тогда и только тогда, когда это так делает в другой норме. В бесконечномерном случае, однако, обычно будут неэквивалентные топологии, что делает изучение топологических векторных пространств более богатым, чем изучение векторных пространств без дополнительных данных.

С концептуальной точки зрения все понятия, относящиеся к топологическим векторным пространствам, должны соответствовать топологии. Например, вместо рассмотрения всех линейных отображений (также называемых функционалами ) V → W, требуется, чтобы отображения между топологическими векторными пространствами были непрерывными. В частности, (топологическое) двойственное пространство V состоит из непрерывных функционалов V → R (или до C ). Фундаментальная теорема Хана – Банаха касается разделения подпространств соответствующих топологических векторных пространств непрерывными функционалами.

Банаховы пространства

Банаховы пространства, введенные Стефаном Банахом, являются полными нормированными векторными пространствами.

Первым примером является векторное пространство $\ell \; p\; \{\backslash \; displaystyle\; \backslash \; ell\; ^\; \{p\}\}$, состоящее из бесконечных векторов с действительными записи $x\; =\; (x\; 1,\; x\; 2,\dots ,\; xn,\dots )\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{x\}\; =\; \backslash \; left\; (x\_\; \{1\},\; x\_\; \{2\},\; \backslash \; ldots,\; x\_\; \{n\},\; \backslash \; ldots\; \backslash \; right)\}$, $p\; \{\backslash \; displaystyle\; p\}$-norm $(1\; \le \; p\; \le \; \infty )\; \{\backslash \; displaystyle\; (1\; \backslash \; leq\; \{p\}\; \backslash \; leq\; \backslash \; infty)\}$, задаваемый

$\Vert \; x\; \Vert \; p:\; =\; (\sum \; i\; |\; xi\; |\; p)\; 1\; p\; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; Vert\; \backslash \; mathbf\; \{x\}\; \backslash \; right\; \backslash \; Vert\; \_\; \{p\}:\; =\; \backslash \; left\; (\backslash \; sum\; \_\; \{i\}\; \backslash \; left\; \backslash \; vert\; x\_\; \{i\}\; \backslash \; right\; \backslash \; vert\; ^\; \{p\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{1\}\; \{p\}\}\}$для и $\Vert \; x\; \Vert \; \infty :\; =\; sup\; i\; |\; х\; я\; |\; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; Vert\; \backslash \; mathbf\; \{x\}\; \backslash \; right\; \backslash \; Vert\; \_\; \{\backslash \; infty\}:\; =\; \{\backslash \; text\; \{sup\}\}\; \_\; \{i\}\; \backslash \; left\; \backslash \; vert\; x\_\; \{i\}\; \backslash \; right\; \backslash \; vert\}$.

Топологии в бесконечномерном пространстве $\ell \; p\; \{\backslash \; displaystyle\; \backslash \; ell\; ^\; \{p\}\}$неэквивалентны для разных $p\; \{\backslash \; displaystyle\; p\}$. Например, последовательность векторов $xn\; =\; (2\; -\; n,\; 2\; -\; n,\dots ,\; 2\; -\; n,\; 0,\; 0,\dots )\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{x\}\; \_\; \{n\}\; =\; \backslash \; left\; (2\; ^\; \{-\; n\},\; 2\; ^\; \{-\; n\},\; \backslash \; ldots,\; 2\; ^\; \{-\; n\},\; 0,0,\; \backslash \; ldots\; \backslash \; right)\}$, в котором первый $2\; n\; \{\; \backslash \; displaystyle\; 2\; ^\; \{n\}\}$компоненты: $2\; -\; n\; \{\backslash \; displaystyle\; 2\; ^\; \{-\; n\}\}$, а следующие: $0\; \{\backslash \; displaystyle\; 0\}$, сходится к нулевому вектору для $p\; =\; \infty \; \{\backslash \; displaystyle\; p\; =\; \backslash \; infty\}$, но не для $p\; Знак\; равно\; 1\; \{\backslash \; displaystyle\; p\; =\; 1\}$:

$\Vert \; xn\; \Vert \; \infty \; =\; sup\; (2\; -\; n,\; 0)\; =\; 2\; -\; n\; \to \; 0\; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; Vert\; \backslash \; mathbf\; \{x\}\; \_\; \{n\}\; \backslash \; right\; \backslash \; Vert\; \_\; \{\_\; \{\backslash \; infty\}\}\; =\; \backslash \; sup\; (2\; ^\; \{-\; n\},\; 0)\; =\; 2\; ^\; \{-\; n\}\; \backslash \; rightarrow\; 0\}$, но $\Vert \; xn\; \Vert \; 1\; =\; \sum \; я\; знак\; равно\; 1\; 2\; N\; 2\; -\; N\; знак\; равно\; 2\; N\; \cdot \; 2\; -\; N\; =\; 1.\; \{\backslash \; Displaystyle\; \backslash \; left\; \backslash \; Vert\; \backslash \; mathbf\; \{x\}\; \_\; \{n\}\; \backslash \; right\; \backslash \; Vert\; \_\; \{1\}\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\; \}\; ^\; \{2\; ^\; \{n\}\}\; 2\; ^\; \{-\; n\}\; =\; 2\; ^\; \{n\}\; \backslash \; cdot\; 2\; ^\; \{-\; n\}\; =\; 1.\}$

В более общем смысле, чем последовательности действительных чисел, функции $f:\; \Omega \; \to \; R\; \{\backslash \; displaystyle\; f\; \backslash \; двоеточие\; \backslash \; Omega\; \backslash \; to\; \backslash \; mathbb\; \{R\}\}$наделены нормой t заменяет указанную выше сумму на интеграл Лебега

$\Vert \; f\; \Vert \; p:\; =\; (\int \; \Omega \; |\; f\; (x)\; |\; p\; d\; \mu \; (x))\; 1\; п.\; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; Vert\; \{f\}\; \backslash \; right\; \backslash \; Vert\; \_\; \{p\}:\; =\; \backslash \; left\; (\backslash \; int\; \_\; \{\backslash \; Omega\}\; \backslash \; left\; \backslash \; vert\; \{f\}\; \backslash \; left\; (x\; \backslash \; right)\; \backslash \; right\; \backslash \; vert\; ^\; \{\; p\}\; \backslash ,\; \{d\; \backslash \; mu\; \backslash \; left\; (x\; \backslash \; right)\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{1\}\; \{p\}\}.\}$

Пространство интегрируемых функций на заданном домен $\Omega \; \{\backslash \; displaystyle\; \backslash \; Omega\}$(например, интервал), удовлетворяющий и снабженный этой нормой, называются Пространства Лебега, обозначаемые $L\; p\; (\Omega )\; \{\backslash \; displaystyle\; L\; ^\; \{\backslash ;\; \backslash !\; P\}\; \backslash \; left\; (\backslash \; Omega\; \backslash \; right)\}$.

Эти пространства полные. (Если вместо этого использовать интеграл Римана, пространство не будет полным, что можно рассматривать как оправдание теории интегрирования Лебега.) Конкретно это означает, что для любой последовательности интегрируемых по Лебегу функций $f\; 1,\; f\; 2,\dots ,\; fn,\dots \; \{\backslash \; displaystyle\; f\_\; \{1\},\; f\_\; \{2\},\; \backslash \; ldots,\; f\_\; \{n\},\; \backslash \; ldots\}$с , удовлетворяющее условию

$lim\; k,\; n\; \to \; \infty \; \int \; \Omega \; |\; f\; k\; (x)\; -\; f\; n\; (x)\; |\; пд\; \mu \; (Икс)\; знак\; равно\; 0\; \{\backslash \; Displaystyle\; \backslash \; lim\; \_\; \{к,\; \backslash \; n\; \backslash \; к\; \backslash \; infty\}\; \backslash \; int\; \_\; \{\backslash \; Omega\}\; \backslash \; left\; \backslash \; vert\; \{f\}\; \_\; \{k\}\; (x)\; -\; \{f\}\; \_\; \{\; n\}\; (x)\; \backslash \; right\; \backslash \; vert\; ^\; \{p\}\; \backslash ,\; \{d\; \backslash \; mu\; \backslash \; left\; (x\; \backslash \; right)\}\; =\; 0\}$

существует функция $f\; (x)\; \{\backslash \; displaystyle\; \{f\}\; \backslash \; left\; (x\; \backslash \; right)\}$принадлежит векторному пространству $L\; p\; (\Omega )\; \{\backslash \; displaystyle\; L\; ^\; \{\backslash ;\; \backslash !\; p\}\; \backslash \; left\; (\backslash \; Omega\; \backslash \; right)\}$такое, что

$lim\; k\; \to \; \infty \; \int \; \Omega \; |\; f\; (x)\; -\; f\; k\; (x)\; |\; пд\; \mu \; (x)\; =\; 0.\; \{\backslash \; displaystyle\; \backslash \; lim\; \_\; \{k\; \backslash \; to\; \backslash \; infty\}\; \backslash \; int\; \_\; \{\backslash \; Omega\}\; \backslash \; left\; \backslash \; vert\; \{f\}\; \backslash \; left\; (x\; \backslash \; right)\; -\; \{f\}\; \_\; \{k\}\; \backslash \; left\; (x\; \backslash \; right)\; \backslash \; right\; \backslash \; vert\; ^\; \{p\}\; \backslash ,\; \{d\; \backslash \; mu\; \backslash \; left\; (x\; \backslash \; right)\}\; =\; 0.\}$

Наложение условий ограниченности не только на функцию, но и на ее производные приводит к пространствам Соболева.

гильбертовым пространствам

Последующие снимки показывают суммирование от 1 до 5 членов при приближении периодической функции (синий) конечной суммой синусоидальных функций (красный).

Полные пространства внутреннего продукта известны как гильбертовы пространства в честь Дэвида Гильберта. Гильбертово пространство L (Ω) со скалярным продуктом, задаваемым

$⟨f,\; g⟩\; =\; \int \; \Omega \; f\; (x)\; g\; (x)\; ¯\; dx,\; \{\backslash \; displaystyle\; \backslash \; langle\; f\; \backslash ,\; \backslash \; g\; \backslash \; rangle\; =\; \backslash \; int\; \_\; \{\backslash \; Omega\}\; f\; (x)\; \{\backslash \; overline\; \{g\; (x)\}\}\; \backslash ,\; dx,\}$

где $g\; (x)\; ¯\; \{\backslash \; displaystyle\; \{\backslash \; overline\; \{g\; (x)\}\}\}$обозначает комплексное сопряжение с g (x), это ключевой случай.

По определению в гильбертовом пространстве любая последовательность Коши сходится к пределу. И наоборот, не менее важно найти последовательность функций f n с желательными свойствами, которая приближает заданную предельную функцию. Ранний анализ под видом приближения Тейлора установил приближение дифференцируемых функций f полиномами. Согласно теореме Стоуна – Вейерштрасса, любую непрерывную функцию на [a, b] можно сколь угодно точно аппроксимировать полиномом. Подобный метод аппроксимации с помощью тригонометрических функций обычно называется разложением Фурье и широко применяется в технике, см. ниже. В более общем плане и более концептуально теорема дает простое описание того, какие «базовые функции» или, в абстрактных гильбертовых пространствах, каких базовых векторов достаточно для генерации гильбертова пространства H, в том смысле, что замыкание их промежутка (то есть конечных линейных комбинаций и их пределов) составляет все пространство. Такой набор функций называется базисом H, его мощность известна как размерность гильбертова пространства. Теорема не только демонстрирует подходящие базисные функции, достаточные для целей аппроксимации, но также вместе с процессом Грама – Шмидта она позволяет построить базис из ортогональных векторов. Такие ортогональные базисы являются обобщением осей координат в гильбертовом пространстве в конечномерном евклидовом пространстве.

Решения различных дифференциальных уравнений могут быть интерпретированы в терминах гильбертовых пространств. Например, очень многие области физики и техники приводят к таким уравнениям, и часто решения с определенными физическими свойствами используются в качестве базисных функций, часто ортогональных. В качестве примера из физики зависящее от времени уравнение Шредингера в квантовой механике описывает изменение физических свойств во времени с помощью уравнения в частных производных, решения называются волновыми функциями. Определенные значения физических свойств, таких как энергия или импульс, соответствуют собственным значениям определенного (линейного) дифференциального оператора, а соответствующие волновые функции называются собственными состояниями. Спектральная теорема разлагает линейный компактный оператор, действующий на функции в терминах этих собственных функций и их собственных значений.

Алгебры над полями

A гипербола, заданная уравнением x ⋅ y = 1. Координатное кольцо функций на этой гиперболе задается R [x, y] / (x · y - 1), бесконечномерным векторным пространством over R.

Общие векторные пространства не обладают умножением между векторами. Векторное пространство, снабженное дополнительным билинейным оператором , определяющим умножение двух векторов, является алгеброй над полем. Многие алгебры происходят из функций на каком-то геометрическом объекте: поскольку функции со значениями в данном поле можно умножать поточечно, эти объекты образуют алгебры. Теорема Стоуна – Вейерштрасса, например, опирается на банаховы алгебры, которые одновременно являются банаховыми пространствами и алгебрами.

Коммутативная алгебра широко использует кольца многочленов от одной или нескольких переменных, введенные выше. Их умножение является как коммутативным, так и ассоциативным. Эти кольца и их частные составляют основу алгебраической геометрии, потому что они являются кольцами функций алгебраических геометрических объектов.

Другим важным примером являются алгебры Ли, которые ни коммутативным или ассоциативным, но несоблюдение этого условия ограничивается ограничениями ([x, y] обозначает произведение x и y):

• [x, y] = - [y, x] (антикоммутативность ) и
• [x, [y, z]] + [y, [z, x]] + [z, [x, y]]] = 0 (тождество Якоби ).

Примеры включают векторное пространство матриц размером n на n с [x, y] = xy - yx, коммутатором двух матриц и R, наделенным перекрестное произведение.

Тензорная алгебра T (V) - это формальный способ добавления произведений к любому векторному пространству V для получения алгебры. Как векторное пространство оно натянуто на символы, называемые простые тензоры

v1⊗ v2⊗ ⋯ ⊗ vn, где степень n изменяется.

Умножение дается путем конкатенации таких символов, налагая закон распределения и Кроме того, требуется, чтобы скалярное умножение коммутировало с тензорным произведением ⊗, почти так же, как с тензорным произведением двух векторных пространств, введенных выше. Как правило, между v1⊗ v2и v2⊗ v1нет никакой связи. Принуждение двух таких элементов к равенству приводит к симметрической алгебре, тогда как принуждение v1⊗ v2= - v2⊗ v1дает внешнюю алгебру.

. Когда поле, F явно указано, общее Используемый термин - F-алгебра.

У векторных пространств есть много приложений, поскольку они часто встречаются в обычных обстоятельствах, а именно там, где задействованы функции со значениями в каком-либо поле. Они обеспечивают основу для решения аналитических и геометрических задач или используются в преобразовании Фурье. Этот список не является исчерпывающим: существует гораздо больше приложений, например, в оптимизации. теорема о минимаксе из теории игр, утверждающая существование уникального выигрыша, когда все игроки играют оптимально, может быть сформулирована и доказана с использованием методов векторных пространств. Теория представлений плодотворно переносится хорошее понимание линейной алгебры и векторных пространств для других математических областей, таких как теория групп.

Распределения

Распределение (или обобщенная функция) - это линейная карта, присваивающая номер каждому " test "функция, обычно сглаженная функция с компактной опорой, непрерывным способом: в выше терминологии пространство распределений - (непрерывное) двойственный к пробному функциональному пространству. Последнее пространство наделено топологией, учитывающей не только само f, но и все его