Войти
Линейная система трех переменных определяет набор плоскостей. Точка пересечения - это решение. В математике, А система линейных уравнений (или линейной системы) представляет собой набор из одного или более линейных уравнений, связанных с тем же набором переменных. Например,
представляет собой систему трех уравнений от трех переменных x, y, z. Решение для линейной системы является присвоение значений переменных, таких, что все уравнения одновременно удовлетворены. Раствора в системе выше задается
поскольку это делает все три уравнения справедливыми. Слово «система» указывает на то, что уравнения следует рассматривать вместе, а не по отдельности.
В математике теория линейных систем является основой и фундаментальной частью линейной алгебры, предмета, который используется в большинстве разделов современной математики. Вычислительные алгоритмы нахождения решений являются важной частью численной линейной алгебры и играют важную роль в инженерии, физике, химии, информатике и экономике. Система нелинейных уравнений часто может быть аппроксимирована линейной системой (см линеаризации ), полезной техникой при принятии математической модели или компьютерного моделирования с относительно сложной системы.
Очень часто коэффициенты уравнений являются действительными или комплексными числами, и решения ищутся в одном и том же наборе чисел, но теория и алгоритмы применимы для коэффициентов и решений в любой области. Для решений в области целостности подобно кольцу из целых чисел, или в других алгебраических структурах, другие теории были разработаны, см линейного уравнения над кольцом. Целочисленное линейное программирование - это набор методов для поиска «лучшего» целочисленного решения (когда их много). Теория базиса Грёбнера предоставляет алгоритмы, когда коэффициенты и неизвестные являются полиномами. Также тропическая геометрия является примером линейной алгебры в более экзотической структуре.
Система одного уравнения с одной неизвестной
есть решение
Однако обычно считается, что линейная система имеет как минимум два уравнения.
Простейший вид нетривиальной линейной системы включает два уравнения и две переменные:
Один из методов решения такой системы заключается в следующем. Во- первых, решить верхнее уравнение в терминах:
Теперь подставьте это выражение для x в нижнее уравнение:
В результате получается одно уравнение, включающее только переменную. Решение дает и подставляет это обратно в уравнение для урожайности. Этот метод обобщается на системы с дополнительными переменными (см. «Исключение переменных» ниже или статью по элементарной алгебре. )
Общая система m линейных уравнений с n неизвестными может быть записана как
где - неизвестные, - коэффициенты системы, - постоянные члены.
Часто коэффициенты и неизвестные являются действительными или комплексными числами, но также видны целые и рациональные числа, а также многочлены и элементы абстрактной алгебраической структуры.
Одно чрезвычайно полезное представление состоит в том, что каждое неизвестное является весом для вектора-столбца в линейной комбинации.
Это позволяет использовать весь язык и теорию векторных пространств (или, в более общем смысле, модулей ). Например, набор всех возможных линейных комбинаций векторов в левой части называется их диапазоном, и уравнения имеют решение именно тогда, когда правый вектор находится внутри этого диапазона. Если каждый вектор в этом диапазоне имеет ровно одно выражение как линейную комбинацию заданных левых векторов, то любое решение уникально. В любом случае диапазон имеет основу из линейно независимых векторов, которые действительно гарантируют ровно одно выражение; и количество векторов в этом базисе (его размерность ) не может быть больше m или n, но может быть меньше. Это важно, потому что, если у нас есть m независимых векторов, решение гарантировано независимо от правой части, а в противном случае не гарантируется.
Векторное уравнение эквивалентно матричному уравнению вида
где A - матрица размера m × n, x - вектор-столбец с n элементами, а b - вектор-столбец с m элементами.
Количество векторов в основе диапазона теперь выражается как ранг матрицы.
Множество решений для уравнений x - y = −1 и 3 x + y = 9 - это единственная точка (2, 3). Решением линейной системы является присвоением значений переменных х 1, х 2,..., х п, такой, что каждый из уравнений удовлетворяются. Множество всех возможных решений называется множество решений.
Линейная система может вести себя одним из трех возможных способов:
Для системы с участием двух переменных ( х и Y), каждое линейное уравнение определяет линию на ху - плоскость. Поскольку решение линейной системы должно удовлетворять всем уравнениям, набор решений является пересечением этих линий и, следовательно, является линией, одной точкой или пустым набором.
Для трех переменных каждое линейное уравнение определяет плоскость в трехмерном пространстве, а набор решений - это пересечение этих плоскостей. Таким образом, набор решений может быть плоскостью, линией, отдельной точкой или пустым набором. Например, поскольку три параллельные плоскости не имеют общей точки, набор решений их уравнений пуст; система решений уравнений трех пересекающихся в точке плоскостей является единственной точкой; если три плоскости проходят через две точки, их уравнения имеют как минимум два общих решения; на самом деле множество решений бесконечно и состоит из всех прямых, проходящих через эти точки.
Для n переменных каждое линейное уравнение определяет гиперплоскость в n- мерном пространстве. Множество решений является пересечением этих гиперплоскостей и представляет собой плоскость, которая может иметь любую размерность меньше n.
Множество решений для двух уравнений с тремя переменными, как правило, представляет собой линию. В общем, поведение линейной системы определяется соотношением между количеством уравнений и количеством неизвестных. Здесь «в целом» означает, что для конкретных значений коэффициентов уравнений может иметь место различное поведение.
В первом случае размерность множества решений, как правило, равна n - m, где n - количество переменных, а m - количество уравнений.
Следующие рисунки иллюстрируют эту трихотомию в случае двух переменных:
 |  |  |
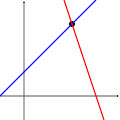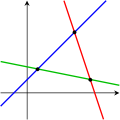| Одно уравнение | Два уравнения | Три уравнения |
Первая система имеет бесконечно много решений, а именно все точки на синей линии. Вторая система имеет единственное единственное решение, а именно пересечение двух линий. Третья система не имеет решений, поскольку три линии не имеют общей точки.
Следует иметь в виду, что на рисунках выше показан только самый частый случай (общий случай). Система из двух уравнений и двух неизвестных может не иметь решения (если две прямые параллельны) или система из трех уравнений и двух неизвестных может быть разрешимой (если три линии пересекаются в одной точке).
Система линейных уравнений ведет себя иначе, чем в общем случае, если уравнения линейно зависимы, или если она несовместима и имеет не больше уравнений, чем неизвестных.
Уравнения линейной системы независимы, если ни одно из уравнений не может быть выведено алгебраически из других. Когда уравнения независимы, каждое уравнение содержит новую информацию о переменных, и удаление любого из уравнений увеличивает размер набора решений. Для линейных уравнений логическая независимость - это то же самое, что и линейная независимость.
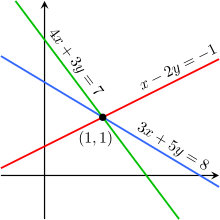Уравнения x - 2 y = −1, 3 x + 5 y = 8 и 4 x + 3 y = 7 линейно зависимы. Например, уравнения
не являются независимыми - они представляют собой одно и то же уравнение при масштабировании в два раза, и они будут давать идентичные графики. Это пример эквивалентности в системе линейных уравнений.
Для более сложного примера уравнения
не являются независимыми, потому что третье уравнение является суммой двух других. Действительно, любое из этих уравнений может быть получено из двух других, и любое из уравнений может быть удалено, не влияя на набор решений. Графики этих уравнений представляют собой три линии, пересекающиеся в одной точке.
Уравнения 3 x + 2 y = 6 и 3 x + 2 y = 12 несовместимы. Линейная система несовместна, если у нее нет решения, в противном случае она называется согласованной. Когда система несовместима, из уравнений можно вывести противоречие, которое всегда можно переписать как утверждение 0 = 1.
Например, уравнения
непоследовательны. Фактически, вычитая первое уравнение из второго и умножая обе части результата на 1/6, мы получаем 0 = 1. Графики этих уравнений на плоскости xy представляют собой пару параллельных линий.
Три линейных уравнения могут быть несовместными, даже если любые два из них согласованы вместе. Например, уравнения
непоследовательны. Сложение первых двух уравнений дает 3 x + 2 y = 2, которые можно вычесть из третьего уравнения и получить 0 = 1. Любые два из этих уравнений имеют общее решение. То же явление может иметь место для любого количества уравнений.
В общем случае несоответствия возникают, если левые части уравнений в системе линейно зависимы, а постоянные члены не удовлетворяют соотношению зависимости. Система уравнений, левые части которой линейно независимы, всегда непротиворечива.
Положив это по- другому, в соответствии с теоремой Руш-Капелл, любая система уравнений (переопределено или иначе) противоречива, если ранг в дополненной матрице больше, чем ранг матрицы коэффициентов. Если, с другой стороны, ранги этих двух матриц равны, система должна иметь хотя бы одно решение. Решение уникально тогда и только тогда, когда ранг равен количеству переменных. В противном случае общее решение имеет k свободных параметров, где k - разница между числом переменных и рангом; следовательно, в таком случае решений бесконечно много. Ранг системы уравнений (т. Е. Ранг расширенной матрицы) никогда не может быть выше, чем [количество переменных] + 1, что означает, что система с любым количеством уравнений всегда может быть сведена к системе, которая имеет количество независимых уравнений, не более чем [количество переменных] + 1.
Две линейные системы, использующие один и тот же набор переменных, эквивалентны, если каждое из уравнений второй системы может быть выведено алгебраически из уравнений первой системы, и наоборот. Две системы эквивалентны, если либо обе несовместны, либо каждое уравнение каждой из них является линейной комбинацией уравнений другой. Отсюда следует, что две линейные системы эквивалентны тогда и только тогда, когда они имеют одно и то же множество решений.
Есть несколько алгоритмов для решения системы линейных уравнений.
Когда множество решений конечно, оно сводится к одному элементу. В этом случае единственное решение описывается, например, последовательностью уравнений, левые части которых являются именами неизвестных, а правые части - соответствующими значениями. Когда порядок неизвестных был установлен, например алфавитный порядок, решение можно описать как вектор значений, как в предыдущем примере.
Чтобы описать набор с бесконечным числом решений, обычно некоторые из переменных обозначаются как свободные (или независимые, или как параметры), что означает, что им разрешено принимать любое значение, в то время как остальные переменные зависят от значений свободные переменные.
Например, рассмотрим следующую систему:
Набор решений этой системы можно описать следующими уравнениями:
Здесь z - свободная переменная, а x и y зависят от z. Любую точку в наборе решений можно получить, сначала выбрав значение для z, а затем вычислив соответствующие значения для x и y.
Каждая свободная переменная дает пространству решений одну степень свободы, количество которой равно размерности множества решений. Например, набор решений для приведенного выше уравнения представляет собой линию, поскольку точку в наборе решений можно выбрать, указав значение параметра z. Бесконечное решение более высокого порядка может описывать плоскость или многомерное множество.
Различный выбор свободных переменных может привести к разному описанию одного и того же набора решений. Например, решение вышеуказанных уравнений можно альтернативно описать следующим образом:
Здесь x - свободная переменная, а y и z - зависимые.
Самый простой метод решения системы линейных уравнений - многократное исключение переменных. Этот метод можно описать следующим образом:
Например, рассмотрим следующую систему:
Решение первого уравнения относительно x дает x = 5 + 2 z - 3 y, а включение этого во второе и третье уравнение дает
Решение первого из этих уравнений относительно y дает y = 2 + 3 z, а включение его во второе уравнение дает z = 2. Теперь у нас есть:
Подстановка z = 2 во второе уравнение дает y = 8, а замена z = 2 и y = 8 в первое уравнение дает x = −15. Следовательно, набором решений является единственная точка ( x, y, z) = (−15, 8, 2).
При сокращении строк (также известном как исключение Гаусса) линейная система представляется в виде расширенной матрицы :
Затем эта матрица модифицируется с использованием элементарных операций со строками до тех пор, пока она не достигнет уменьшенной формы эшелона строк. Есть три типа операций с элементарными строками:
Поскольку эти операции обратимы, полученная расширенная матрица всегда представляет собой линейную систему, эквивалентную исходной.
Существует несколько конкретных алгоритмов сокращения строк расширенной матрицы, простейшие из которых - исключение Гаусса и исключение Гаусса – Жордана. Следующее вычисление показывает применение метода исключения Гаусса – Жордана к матрице выше:
Последняя матрица представлена в виде сокращенного эшелона строк и представляет систему x = −15, y = 8, z = 2. Сравнение с примером алгебраического исключения переменных из предыдущего раздела показывает, что эти два метода фактически одинаковы; разница заключается в том, как записываются вычисления.
Правило Крамера - это явная формула для решения системы линейных уравнений, в которой каждая переменная задается частным двух определителей. Например, решение системы
дан кем-то
Для каждой переменной знаменатель является определителем матрицы коэффициентов, а числитель - определителем матрицы, в которой один столбец заменен вектором постоянных членов.
Хотя правило Крамера важно теоретически, оно не имеет практического значения для больших матриц, поскольку вычисление больших детерминантов несколько громоздко. (Действительно, большие детерминанты легче всего вычислить с помощью сокращения строк.) Кроме того, правило Крамера имеет очень плохие числовые свойства, что делает его непригодным для надежного решения даже небольших систем, если операции не выполняются в рациональной арифметике с неограниченной точностью.
Если система уравнений выражена в матричной форме, весь набор решений также может быть выражен в матричной форме. Если матрица A квадратная (имеет m строк и n = m столбцов) и имеет полный ранг (все m строк независимы), то система имеет единственное решение, задаваемое формулой
где есть обратная из A. В более общем плане, независимо от того, m = n или нет, и независимо от ранга A, все решения (если таковые существуют) даются с использованием псевдообратного выражения Мура-Пенроуза для A, обозначаемого следующим образом:
где - вектор свободных параметров, который пробегает все возможные векторы n × 1. Необходимым и достаточным условием для существования любого решения (й) является то, что потенциальное решение, полученное с помощью, удовлетворяет - то есть, если это условие не выполняется, система уравнений несовместима и не имеет решения. Если условие выполняется, система непротиворечива и существует хотя бы одно решение. Например, в вышеупомянутом случае, когда A квадратное и полного ранга, просто равно, и уравнение общего решения упрощается до
как указывалось ранее, где полностью выпал из решения, оставив только одно решение. В других случаях, однако, остается и, следовательно, бесконечное количество потенциальных значений свободного вектора параметров дает бесконечное количество решений уравнения.
В то время как системы из трех или четырех уравнений могут быть легко решены вручную (см. Краковский ), компьютеры часто используются для более крупных систем. Стандартный алгоритм решения системы линейных уравнений основан на методе исключения Гаусса с некоторыми изменениями. Во-первых, важно избегать деления на маленькие числа, так как это может привести к неточным результатам. Это можно сделать, при необходимости переупорядочив уравнения - процесс, известный как поворот. Во- вторых, алгоритм точно не делать исключения Гаусса, но он вычисляет разложение LU матрицы A. В основном это организационный инструмент, но он работает намного быстрее, если нужно решать несколько систем с одной и той же матрицей A, но с разными векторами b.
Если матрица A имеет особую структуру, ее можно использовать для получения более быстрых или более точных алгоритмов. Например, системы с симметричной положительно определенной матрицей могут быть решены в два раза быстрее с помощью разложения Холецкого. Рекурсия Левинсона - это быстрый метод для матриц Теплица. Специальные методы существуют также для матриц с большим количеством нулевых элементов (так называемые разреженные матрицы ), которые часто используются в приложениях.
Совершенно другой подход часто используется для очень больших систем, которые в противном случае потребовали бы слишком много времени или памяти. Идея состоит в том, чтобы начать с начального приближения к решению (которое совсем не обязательно должно быть точным) и изменить это приближение в несколько шагов, чтобы приблизить его к истинному решению. Если приближение достаточно точное, оно считается решением системы. Это приводит к классу итерационных методов. Для некоторых разреженных матриц введение случайности увеличивает скорость итерационных методов.
Также существует квантовый алгоритм для линейных систем уравнений.
Система линейных уравнений однородна, если все постоянные члены равны нулю:
Однородная система эквивалентна матричному уравнению вида
где A - матрица размера m × n, x - вектор-столбец с n элементами, а 0 - нулевой вектор с m элементами.
Каждая однородная система имеет по крайней мере одно решение, известное как нулевое (или тривиальное) решение, которое получается путем присвоения значения нуля каждой из переменных. Если система имеет невырожденную матрицу ( det ( A) 0), то это также единственное решение. Если система имеет сингулярную матрицу, то существует множество решений с бесконечным числом решений. Этот набор решений имеет следующие дополнительные свойства:
Это в точности те свойства, которые необходимы для того, чтобы набор решений был линейным подпространством в R n. В частности, множество решений для однородной системы является такой же, как нулевое пространство соответствующей матрицы A. Численные решения однородной системы могут быть найдены с помощью сингулярного разложения.
Существует тесная связь между решениями линейной системы и решениями соответствующей однородной системы:
В частности, если p - любое конкретное решение линейной системы A x = b, то весь набор решений можно описать как
С геометрической точки зрения это означает, что набор решений для A x = b является переводом набора решений для A x = 0. В частности, плоскость для первой системы может быть получена путем переноса линейного подпространства для однородной системы на вектор p.
Это рассуждение применимо только в том случае, если система A x = b имеет хотя бы одно решение. Это происходит тогда и только тогда, когда вектор Ь лежит в изображении от линейного преобразования A.
СМИ, связанные с Системой линейных уравнений на Викискладе?
![\ left [{\ begin {array} {rrr | r} 1 amp; 3 amp; -2 amp; 5 \\ 3 amp; 5 amp; 6 amp; 7 \\ 2 amp; 4 amp; 3 amp; 8 \ end {array}} \ right] {\ text {.}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d99c79eb45b325d779be9693c613d9aec07b6d4)
![{\ begin {align} \ left [{\ begin {array} {rrr | r} 1 amp; 3 amp; -2 amp; 5 \\ 3 amp; 5 amp; 6 amp; 7 \\ 2 amp; 4 amp; 3 amp; 8 \ end {array}} \ right] amp; \ sim \ left [{\ begin {array} {rrr | r} 1 amp; 3 amp; -2 amp; 5 \\ 0 amp; -4 amp; 12 amp; -8 \\ 2 amp; 4 amp; 3 amp; 8 \ end {array}} \ right] \ sim \ left [{\ begin {array} {rrr | r} 1 amp; 3 amp; -2 amp; 5 \\ 0 amp; - 4 amp; 12 amp; -8 \\ 0 amp; -2 amp; 7 amp; -2 \ end {array}} \ right] \ sim \ left [{\ begin {array} {rrr | r} 1 amp; 3 amp; -2 amp; 5 \\ 0 amp; 1 amp; -3 amp; 2 \\ 0 amp; -2 amp; 7 amp; -2 \ end {array}} \ right] \\ amp; \ sim \ left [{\ begin {array} {rrr | r} 1 amp; 3 amp; -2 amp; 5 \\ 0 amp; 1 amp; -3 amp; 2 \\ 0 amp; 0 amp; 1 amp; 2 \ end {array}} \ right] \ sim \ left [{\ begin {array} {rrr | r} 1 amp; 3 amp; -2 amp; 5 \\ 0 amp; 1 amp; 0 amp; 8 \\ 0 amp; 0 amp; 1 amp; 2 \ end {array}} \ right] \ sim \ left [{\ begin {array} {rrr | r} 1 amp; 3 amp; 0 amp; 9 \ \ 0 amp; 1 amp; 0 amp; 8 \\ 0 amp; 0 amp; 1 amp; 2 \ end {array}} \ right] \ sim \ left [{\ begin {array} {rrr | r} 1 amp; 0 amp; 0 amp; -15 \\ 0 amp; 1 amp; 0 amp; 8 \\ 0 amp; 0 amp; 1 amp; 2 \ end {array}} \ right]. \ конец {выровнен}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f6367f306a7947555dd25f9b3b29a5903efdabb)
