Определитель

В линейной алгебре, инварианте квадратных матриц и эндоморфизмов

В линейной алгебре, определитель - это скалярное значение , которое может быть вычислено из элементов квадратной матрицы и кодирует верх свойства линейного преобразования, описанного матрица. Определитель матрицы A обозначается det (A), det A или | А |, Геометрически его можно рассматривать как коэффициент масштабирования объема линейного преобразования, описываемого матрицей. Это также знаковый объем n-мерного параллелепипеда, натянутого на горизонт столбцов или матрицы матрицы. Детерминант является положительным или отрицательным в зависимости от того, поддерживает ли линейное преобразование или меняет ориентацию действительного пространства .

или меняет его на противоположное. 928>| А | = | а б в г | = а г - б в. {\ displaystyle {\ begin {align} | А | = {\ begin {vmatrix} a b \\ c d \ end {vmatrix}} = ad-bc. \ end {align}}}

Аналогично для 3 × 3 матрицы A, ее определитель

$|\; А\; |\; =\; |\; а\; б\; в\; г\; д\; е\; ж\; з\; я\; |\; =\; а\; |\; e\; f\; h\; i\; |\; -\; б\; |\; d\; f\; g\; i\; |\; +\; c\; |\; д\; д\; г\; ч\; |\; =\; a\; e\; i\; +\; b\; f\; g\; +\; c\; d\; h\; -\; c\; e\; g\; -\; b\; d\; i\; -\; a\; f\; h.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; |\; А\; |\; =\; \{\backslash \; begin\; \{vmatrix\}\; a\; b\; c\; \backslash \backslash \; d\; e\; f\; \backslash \backslash \; g\; h\; i\; \backslash \; end\; \{vmatrix\}\}\; =\; a\; \backslash ,\; \{\backslash \; begin\; \{vmatrix\}\; e\; f\; \backslash \backslash \; h\; i\; \backslash \; end\; \{vmatrix\}\}\; -\; b\; \backslash ,\; \{\backslash \; begin\; \{vmatrix\}\; d\; f\; \backslash \backslash \; g\; i\; \backslash \; end\; \{vmatrix\}\}\; +\; c\; \backslash ,\; \{\backslash \; begin\; \{vmatrix\}\; d\; e\; \backslash \backslash \; g\; h\; \backslash \; конец\; \{vmatrix\}\}\; \backslash \backslash \; [3pt]\; =\; aei\; +\; bfg\; +\; cdh-ceg-bdi-afh.\; \backslash \; end\; \{align\}\}\}$

Каждый определитель матрицы 2 × 2 в этом уравнении называется второстепенным матрицами A. Эта процедура может быть расширена, чтобы дать рекурсивное определение определителя матрицы размера n × n, известное как расширение Лапласа.

Детерминанты встречаются во всей математике. Например, матрица часто используется для представления коэффициентов в системе линейных уравнений, а определитель может быть решения эти уравнения, хотя другие методы решения более эффективны в вычислительном отношении. В линейной алгебре матрица (с элементами в поле ) является сингулярной (не обратной ) тогда и только тогда, когда ее определитель равен нулю. Это приводит к использованию определителей при определении характеристик полинома матрицы, корнями которых являются собственные значения. В аналитической геометрии определены n-мерные объемы n-мерных параллелепипедов со знаком. Это приводит к использованию определителей в исчислении, определителя Якоби в правиле замены числа для интегралов от функций нескольких чисел. Детерминанты часто появляются в алгебраических тождествах, таких как тождество Вандермонда.

Детерминанты обладают широкими алгебраическими свойствами. Один из них - мультипативность, а именно, что определитель произведения матриц равенство произведению определителей. Специальные типы матриц имеют специальные определители; например, определитель ортогональной матрицы всегда равен плюс или минус один, а определитель комплексной эрмитовой матрицы всегда вещественный.

• 1 Геометрический смысл
• 2 Определение
  • 2.1 Матрицы 2 × 2
  • 2.2 Матрицы 3 × 3
    • 2.2.1 Формула Лапласа
    • 2.2.2 Формула Лейбница
    • 2.2.3 Схема Сарруса
  • 2.3 матрицы размера n × n
    • 2.3.1 Символ Леви-Чивиты
• 3 Свойства определителя
  • 3.1 Дополнение Шура
  • 3.2 Мультипликативность и группы матриц
  • 3.3 Разложение Лапласа и сопряженная матрица
  • 3.4 Теорема Сильвестра о детерминанте
• 4 Свойства определителя по отношению к другим понятиям
  • 4.1 Отношение к собственным значениям и трассе
  • 4.2 Верхняя и нижняя границы
  • 4.3 Правило Крамера
  • 4.4 Блочные
  • 4.5 Производная
• 5 Аналогичные алгебраические аспекты
  • 5.1 Детерминант эндоморфизма
  • 5.2 Внешняя алгебра
  • 5.3 Квадратные матрицы над коммутативными кольцами и а бранные свойства
• 6 Обобщения и связанные понятия
  • 6.1 Бесконечные матрицы
  • 6.2 Операторы в алгебрах фон Неймана
  • 6.3 Связанные понятия для некоммутативных колец
  • 6.4 Другие варианты
• 7 Вычисление
  • 7.1 Методы разложения
  • 7.2 Далее методы
• 8 История
• 9 Приложения
  • 9.1 Линейная независимость
  • 9.2 Ориентация базиса
  • 9.3 Детерминант объема и Якобиана
  • 9.4 Детерминант Вандермонда (альтернатива)
  • 9.5 Циркулянты
• 10 См. Также
• 11 Примечания
• 12 Ссылки
• 13 Внешние ссылки

Если матрица A n × n вещественная записана в терминах ее информационных-столбцов $A\; =\; [a\; 1\; a\; 2\; \cdots \; an]\; \{\backslash \; displaystyle\; A\; =\; [\{\backslash \; begin\; \{array\}\; \{c\; |\; c\; |\; c\; |\; c\}\; \backslash \; mathbf\; \{a\}\; \_\; \{1\}\; \backslash \; mathbf\; \{a\}\; \_\; \{2\}\; \backslash \; cdots\; \backslash \; mathbf\; \{a\}\; \_\; \{n\}\; \backslash \; end\; \{array\}\}]\}$, тогда

$A\; (1\; 0\; ⋮\; 0)\; =\; a\; 1,\; A\; (0\; 1\; 0)\; =\; a\; 2,\dots ,\; A\; (0\; 0\; 1)\; =\; an.\; \{\backslash \; displaystyle\; A\; \{\backslash \; begin\; \{pmatrix\}\; 1\; \backslash \backslash \; 0\; \backslash \backslash \backslash \; vdots\; \backslash \backslash \; 0\; \backslash \; end\; \{pmatrix\}\}\; =\; \backslash \; mathbf\; \{a\}\; \_\; \{1\},\; \backslash \; quad\; A\; \{\backslash \; begin\; \{pmatrix\}\; 0\; \backslash \backslash \; 1\; \backslash \backslash \backslash \; vdots\; \backslash \backslash \; 0\; \backslash \; end\; \{pmatrix\}\}\; =\; \backslash \; mathbf\; \{a\}\; \_\; \{2\},\; \backslash \; quad\; \backslash \; ldots,\; \backslash \; quad\; A\; \{\backslash \; begin\; \{pmatrix\}\; 0\; \backslash \backslash \; 0\; \backslash \backslash \backslash \; vdots\; \backslash \backslash \; 1\; \backslash \; end\; \{pmatrix\}\}\; =\; \backslash \; mathbf\; \{a\}\; \_\; \{n\}.\}$

Это означает, что $A\; \{\backslash \; displaystyle\; A\}$отображает единицу n-куб в n-мерный параллелоэдр, определяемый векторми $a\; 1,\; a\; 2,\dots ,\; an,\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{a\}\; \_\; \{1\},\; \backslash \; mathbf\; \{a\}\; \_\; \{2\},\; \backslash \; ldots,\; \backslash \; mathbf\; \{a\}\; \_\; \{n\},\}$область $P\; =\; \{c\; 1\; a\; 1\; +\; \cdots \; +\; cnan\; \mid \; 0\; \le \; ci\; \le \; 1\; \forall \; i\}.\; \{\backslash \; displaystyle\; P\; =\; \backslash \; left\; \backslash \; \{c\_\; \{1\}\; \backslash \; mathbf\; \{a\}\; \_\; \{1\}\; +\; \backslash \; cdots\; +\; c\_\; \{n\}\; \backslash \; mathbf\; \{a\}\; \_\; \{n\}\; \backslash \; mid\; 0\; \backslash \; leq\; c\_\; \{i\}\; \backslash \; leq\; 1\; \backslash \; \backslash \; forall\; i\; \backslash \; right\; \backslash \}.\}$

Определитель дает подписанный n-мерный объем этого параллелоэдра, $det\; (A)\; =\; \pm \; vol\; (P),\; \{\backslash \; displaystyle\; \backslash \; det\; (\; A)\; =\; \backslash \; pm\; \{\backslash \; text\; \{vol\}\}\; (P),\}$и, следовательно, в более общем плане масштабный коэффициент n-мерного объема линейного преобразования, производимого A. (Знак показывает, поддерживает ли преобразование или меняет ориентацию ориентацию на обратную.) В частности, если определитель равен нулю, то этот параллелоэдр имеет нулевой объем и не является полностью n-мерным, что означает, что размерность образ A меньше п. Это означает, что A линейное преобразование, которое не является ни на, ни взаимно-однозначным, и поэтому не является обратимым.

Существуют различные эквивалентные способы определения определителя квадратной матрицы A, то есть матрицы с одинаковыми строками и столбцов. Возможно, самый простой способ выразить определитель - рассмотреть элементы в верхней строке и соответствующие миноры ; начиная слева, умножьте элемент на второстепенный, затем вычтите следующий элемент и его второстепенное добавление и вычитание таких произведений, пока не будут исерпаны все элементы в верхней строке. Например, вот результат для матрицы 4 × 4:

$|\; а\; б\; в\; г\; д\; е\; ж\; з\; и\; к\; л\; м\; н\; о\; п\; |\; =\; а\; |\; е\; ж\; з\; дж\; к\; л\; н\; о\; п\; |\; -\; б\; |\; э\; г\; х\; и\; к\; л\; м\; о\; п\; |\; +\; c\; |\; д\; е\; з\; и\; дж\; л\; м\; п\; |\; -\; d\; |\; д\; е\; ж\; и\; к\; м\; н\; о\; |.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{vmatrix\}\; a\; b\; c\; d\; \backslash \backslash \; e\; f\; g\; h\; \backslash \backslash \; i\; j\; k\; l\; \backslash \backslash \; m\; n\; o\; p\; \backslash \; end\; \{vmatrix\}\}\; =\; a\; \backslash ,\; \{\backslash \; begin\; \{vmatrix\}\; f\; g\; h\; \backslash \backslash \; j\; k\; l\; \backslash \backslash \; n\; o\; p\; \backslash \; end\; \{vmatrix\}\}\; -\; b\; \backslash ,\; \{\backslash \; begin\; \{vmatrix\}\; e\; g\; h\; \backslash \; \backslash \; i\; k\; l\; \backslash \backslash \; m\; o\; p\; \backslash \; end\; \{vmatrix\}\}\; +\; c\; \backslash ,\; \{\backslash \; begin\; \{vmatrix\}\; e\; f\; h\; \backslash \backslash \; i\; j\; l\; \backslash \backslash \; m\; n\; p\; \backslash \; end\; \{vmatrix\}\}\; -\; d\; \backslash ,\; \{\backslash \; begin\; \{vmatrix\}\; e\; f\; g\; \backslash \backslash \; i\; j\; k\; \backslash \backslash \; m\; n\; o\; \backslash \; end\; \{vmatrix\}\}.\}$

Другой способ определения определителя выражается в терминах столбцов матрицы. Если мы запишем матрицу A размера n × n через ее структуру-столбцы

$A\; =\; [a\; 1\; a\; 2\; \cdots \; an]\; \{\backslash \; displaystyle\; A\; =\; \{\backslash \; begin\; \{bmatrix\}\; a\_\; \{1\}\; a\_\; \{2\}\; \backslash \; cdots\; a\_\; \{n\}\; \backslash \; end\; \{bmatrix\}\}\}$

где $aj\; \{\backslash \; displaystyle\; a\_\; \{j\}\}$- технический размер n, тогда определитель A определяется так, что

$det\; [a\; 1\; \cdots \; baj\; +\; cv\; \cdots \; an]\; =\; b\; det\; (A)\; +\; c\; det\; [a\; 1\; \cdots \; v\; \cdots \; an]\; det\; [a\; 1\; \cdots \; ajaj\; +\; 1\; \cdots \; an]\; =\; -\; det\; [a\; 1\; \cdots \; aj\; +\; 1\; aj\; \cdots \; an]\; det\; (I)\; =\; 1\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; det\; \{\backslash \; begin\; \{bmatrix\}\; a\_\; \{1\}\; \backslash \; cdots\; ba\_\; \{j\}\; +\; cv\; \backslash \; cdots\; a\_\; \{n\}\; \backslash \; end\; \{\; bmatrix\}\}\; =\; b\; \backslash \; det\; (A)\; +\; c\; \backslash \; det\; \{\backslash \; begin\; \{bmatrix\}\; a\_\; \{1\}\; \backslash \; cdots\; v\; \backslash \; cdots\; a\_\; \{n\}\; \backslash \; end\; \{bmatrix\}\}\; \backslash \backslash \backslash \; det\; \{\backslash \; begin\; \{bmatrix\}\; a\_\; \{1\}\; \backslash \; cdots\; a\_\; \{j\}\; a\_\; \{j\; +\; 1\}\; \backslash \; cdots\; a\_\; \{n\}\; \backslash \; end\; \{bmatrix\}\}\; =\; -\; \backslash \; det\; \{\backslash \; begin\; \{bmatrix\}\; a\_\; \{\; 1\}\; \backslash \; cdots\; a\_\; \{j\; +\; 1\}\; a\_\; \{j\}\; \backslash \; cdots\; a\_\; \{n\}\; \backslash \; end\; \{bmatrix\}\}\; \backslash \backslash \backslash \; det\; (I)\; =\; 1\; \backslash \; end\; \{align\}\}\}$

где b и c - скаляры, v - любой вектор размера n, а I - единичная матрица размера п. Эти уравнения указывают на то, что определена функция каждого столбца. который отображает единичную матрицу на базовый единичный скаляр. Этого достаточно, чтобы однозначно вычислить определитель любой квадратной матрицы. При условии, что лежащий в основе скаляры поле (в более общем, коммутативное кольцо ), приведенное ниже определение показывает, что такая функция существует и может быть как уникальная.

Эквивалентно Определитель может быть выражен как сумма произведенных элементов матрицы, где коэффициент каждого продукта равен -1, 1 или 0 в соответствии с заданными правилами: это полиномиальное выражение элементов матрицы. Это выражение быстро растет с размером матрицы (матрица n × n имеет n! ), поэтому сначала оно будет явно дано для случая матриц 2 × 2 и матриц 3 × 3, а по правилам для матриц произвольного размера, которое включает эти два случая.

Предположим, A - квадратная матрица с n строками и n столбцами, так что ее можно записать как

$A\; =\; [a\; 1,\; 1\; a\; 1,\; 2\dots \; a\; 1,\; na\; 2,\; 1\; a\; 2,\; 2\dots \; a\; 2,\; n\; ⋮\; ⋮\; \ddots \; ⋮\; an,\; 1\; an,\; 2\dots \; an,\; n].\; \{\backslash \; displaystyle\; A\; =\; \{\backslash \; begin\; \{bmatrix\}\; a\_\; \{1,1\}\; a\_\; \{1,2\}\; \backslash \; dots\; a\_\; \{1,\; n\}\; \backslash \backslash \; a\_\; \{2,1\}\; a\_\; \{2,2\}\; \backslash \; dots\; a\_\; \{2,\; n\}\; \backslash \backslash \backslash \; vdots\; \backslash \; vdots\; \backslash \; ddots\; \backslash \; vdots\; \backslash \backslash \; a\_\; \{n,\; 1\}\; a\_\; \{n,\; 2\}\; \backslash \; dots\; a\_\; \{n,\; n\}\; \backslash \; end\; \{\; bmatrix\}\}.\}$

Записи могут быть числами или выражениями (как это происходит, когда определитель используется для определения характерного полинома ); определение определяется только от того факта, что их можно складывать и умножать вместе коммутативным способом.

Определитель обозначается как det (A), или его можно обозначить непосредственно в терминах элементов матрицы, написав закрывающие черты вместо скобок:

$|\; a\; 1,\; 1\; a\; 1,\; 2\dots \; a\; 1,\; n\; a\; 2,\; 1\; a\; 2,\; 2\dots \; a\; 2,\; n\; ⋮\; ⋮\; \ddots \; ⋮\; a\; n,\; 1\; a\; n,\; 2\dots \; a\; n,\; n\; |.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{vmatrix\}\; a\_\; \{1,1\}\; a\_\; \{1,2\}\; \backslash \; dots\; a\_\; \{1,\; n\}\; \backslash \backslash \; a\_\; \{2,1\}\; a\_\; \{2,2\}\; \backslash \; dots\; a\_\; \{2,\; n\}\; \backslash \backslash \backslash \; vdots\; \backslash \; vdots\; \backslash \; ddots\; \backslash \; vdots\; \backslash \backslash \; a\_\; \{n,\; 1\}\; a\_\; \{n,\; 2\}\; \backslash \; dots\; a\_\; \{n,\; n\}\; \backslash \; end\; \{vmatrix\}\; \}.\}$

Матрицы 2 × 2

Площадь параллелограмма - это абсолютное значение определителя матрицы, представленной стороны параллелограммы.

Формула Лейбница для определителя 2 × 2 матрица:

$|\; а\; б\; в\; г\; |\; =\; а\; г\; -\; б\; в.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{vmatrix\}\; a\; b\; \backslash \backslash \; c\; d\; \backslash \; end\; \{vmatrix\}\}\; =\; ad-bc.\}$

Если матрицы являются действительными числами, матрица A может быть ap для представлений двух линейных : тот, который отображает стандартные базисные изображения в строки A, и второй, который отображает их в столбцы A. В любом случае изображения изображений векторов образуют параллелограммы , представляет изображение единичного квадрата под отображением. Параллелограмм, определяемый строками вышеприведенной матрицы, - это параллелограмм с вершинами в точках (0, 0), (a, b), (a + c, b + d) и (c, d), как показано на прилагаемых диаграмма.

Абсолютное значение ad - bc - это площадь параллелограмма и таким образом представляет собой коэффициент масштабирования, на котором площади преобразуются с помощью A. симметричен относительно строк и столбцов, площадь будет такой же.)

Абсолютное значение определителя вместе со знаком становится ориентированной площади параллелограмма. Ориентированная область такая же, как и обычная область , за исключением того, что она отрицательна, когда угол от второму вектору, определяющий параллелограмм, поворачивается по часовой стрелке (что противоположно направление, в котором можно было бы получить для единичной матрицы ).

Чтобы показать, что ad - bc является областью со знаком, можно рассмотреть матрицу, содержащую два года u ≡ (a, b) и v ≡ (c, г) изображающие стороны параллелограмма. Знаковая область может быть выражена как | и | | v | sin θ для угла θ между вектором, который является просто основанием, умноженным на высоту, длиной одного вектора, умноженную на перпендикулярную составляющую другое. Благодаря синусу это уже знаковая область, но ее можно выразить более удобно, используя косинус дополнительный угол к перпендикулярному вектору, например u = (-b, a), так что | и | | v | cos θ ′, который может быть определен шаблоном скалярного произведения как равный ad - bc:

$Зона\; со\; знаком\; =\; |\; u\; |\; |\; v\; |\; грех\; \theta \; =\; |\; u\; \perp \; |\; |\; v\; |\; cos\; \theta \; \prime \; =\; (-\; b\; a)\; \cdot \; (c\; d)\; =\; a\; d\; -\; b\; c.\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{Подписанная\; область\}\}\; =\; |\; \{\backslash \; boldsymbol\; \{u\}\}\; |\; \backslash ,\; |\; \{\backslash \; boldsymbol\; \{v\}\}\; |\; \backslash ,\; \backslash \; sin\; \backslash ,\; \backslash \; theta\; =\; \backslash \; left\; |\; \{\backslash \; boldsymbol\; \{u\}\}\; ^\; \{\backslash \; perp\}\; \backslash \; right\; |\; \backslash ,\; \backslash \; влево\; |\; \{\backslash \; boldsymbol\; \{v\}\}\; \backslash \; right\; |\; \backslash ,\; \backslash \; cos\; \backslash ,\; \backslash \; theta\; \text{'}=\; \{\backslash \; begin\; \{pmatrix\}\; -b\; \backslash \backslash \; a\; \backslash \; end\; \{pmatrix\}\}\; \backslash \; cdot\; \{\backslash \; begin\; \{pmatrix\}\; c\; \backslash \backslash \; d\; \backslash \; end\; \{pmatrix\}\}\; =\; ad-bc.\; \}$

Таким образом, определитель дает коэффициент масштабирования и ориентации, индуцированную отображением представленным A. Когда определенное равное единице, линейное отображение определяемое матрицей, является равноплощадным и сохраненной ориентацией.

Известный как бивектор , связан с этими идеями. В 2D это можно интерпретировать как ориентированный сегмент плоскости, образованный путем представления двух векторов, каждый из которых имеет начало координат (0, 0) и координаты (a, b) и (c, d). Величина бивектора (обозначается (a, b) ∧ (c, d)) - это область со знаком, которая также является определителем ad - bc.

Матрицы 3 × 3

Объем этого параллелепипед - абсолютное значение определителя матрицы, образованной столбцами, построенными из векторов r1, r2 и r3.

Формула Лапласа

Формула Лапласа для определителя матрицы 3 × 3 равно

$|\; а\; б\; в\; г\; д\; е\; ж\; з\; я\; |\; =\; а\; |\; e\; f\; h\; i\; |\; -\; б\; |\; d\; f\; g\; i\; |\; +\; c\; |\; д\; д\; г\; ч\; |\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{vmatrix\}\; a\; b\; c\; \backslash \backslash \; d\; e\; f\; \backslash \backslash \; g\; h\; i\; \backslash \; end\; \{vmatrix\}\}\; =\; a\; \{\backslash \; begin\; \{vmatrix\}\; e\; f\; \backslash \backslash \; h\; i\; \backslash \; end\; \{vmatrix\}\}\; -\; b\; \{\backslash \; begin\; \{vmatrix\}\; d\; f\; \backslash \; \backslash \; g\; i\; \backslash \; end\; \{vmatrix\}\}\; +\; c\; \{\backslash \; begin\; \{vmatrix\}\; d\; e\; \backslash \backslash \; g\; h\; \backslash \; end\; \{vmatrix\}\}\; \}$

это можно получить, чтобы получить формулу Лейбница.

Формула Лейбница

Формула Лейбница для определителя матрицы 3 × 3:

$|\; а\; б\; в\; г\; д\; е\; ж\; з\; я\; |\; =\; a\; (e\; i\; -\; f\; h)\; -\; b\; (d\; i\; -\; f\; g)\; +\; c\; (d\; h\; -\; e\; g)\; =\; a\; e\; i\; +\; b\; f\; g\; +\; c\; d\; h\; -\; c\; e\; g\; -\; b\; d\; i\; -\; a\; f\; h.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \{\backslash \; begin\; \{vmatrix\}\; a\; b\; c\; \backslash \backslash \; d\; e\; f\; \backslash \backslash \; g\; h\; i\; \backslash \; end\; \{vmatrix\}\}\; =\; a\; (ei-fh)\; -b\; (ди-фг)\; +\; с\; (дх-например)\; \backslash \backslash \; =\; аей\; +\; бфг\; +\; cdh-ceg-bdi-afh\; \backslash \; end\; \{align\}\}\}$

Схема Сарруса

Правило Сарруса - мнемоника для Определитель матрицы 3 × 3: сумма произведений трех диагональных элементов линий матрицы с северо-запада на юго-восток за вычетом суммы произведений трех диагональных линий элементов с юго-запада на северо-восток, когда копии первых двух столбца матрицы записываются рядом с ней, как на иллюстрации:

$|\; а\; б\; в\; д\; е\; ж\; з\; и\; к\; |\; =\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; ~~~~~~\; \{\backslash \; begin\; \{vmatrix\}\; a\; b\; c\; \backslash \backslash \; e\; f\; g\; \backslash \backslash \; h\; i\; j\; \backslash \; end\; \{vmatrix\}\}\; =\; \backslash \; end\; \{align\}\}\}$ $=\; afj\; +\; bgh\; +\; cei\; -\; hfc\; -\; iga\; -\; jeb\; \{\backslash \; displaystyle\; \backslash \; qquad\; =\; \backslash \; color\; \{red\}\; \{afj\; +\; bgh\; +\; cei\}\; \backslash \; color\; \{blue\}\; \{-\; hfc-iga-jeb\; \}\}$

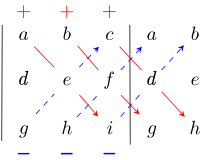
Эта схема вычисления определителя матрица 3 × 3 не переносится в более высокие измерения.

Матрицы n × n

Определитель матрицы произвольного размера может быть определен с помощью формулы Лейбница или формулы Лапласа.

Формула Лейбница для определителя матрицы A размера n × n равен

$det\; (A)\; =\; \sum \; \sigma \; \in \; S\; n\; (sgn\; \; (\sigma )\; \prod \; i\; =\; 1\; nai,\; \sigma \; i).\; \{\backslash \; displaystyle\; \backslash \; det\; (A)\; =\; \backslash \; sum\; \_\; \{\backslash \; sigma\; \backslash \; in\; S\_\; \{n\}\}\; \backslash \; left\; (\backslash \; operatorname\; \{sgn\}\; (\backslash \; sigma)\; \backslash \; prod\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; a\_\; \{i,\; \backslash \; sigma\; \_\; \{i\}\}\; \backslash \; right).\}$

Здесь сумма вычисляется по всем перестановкам σ набора {1, 2,..., n}. Перестановка - это функция, которая переупорядочивает этот набор целых чисел. Значение в i-й позиции после переупорядочения σ обозначается σ i. Например, для n = 3 исходная последовательность 1, 2, 3 может быть переупорядочена в σ = [2, 3, 1], с σ 1 = 2, σ 2 = 3 и σ 3 = 1. Набор всех таких перестановок (также известный как симметрическая группа на n элементах) обозначается S n. Для каждой перестановки σ sign (σ) обозначает подпись σ, значение, которое равно +1 всякий раз, когда переупорядочение, заданное σ, может быть достигнуто путем последовательной замены двух записей четное количество раз, и −1 всякий раз, когда это может быть достигнуто нечетным числом таких обменов.

В любом из $n!\; \{\backslash \; displaystyle\; n!\}$слагаемые, член

$\prod \; i\; =\; 1\; nai,\; \sigma \; i\; \{\backslash \; displaystyle\; \backslash \; prod\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; a\_\; \{i,\; \backslash \; sigma\; \_\; \{i\; \}\}\}$

- это обозначение произведений записей в позициях (i, σ i), где i изменяется от 1 до n:

$a\; 1,\; \sigma \; 1\; \cdot \; a\; 2,\; \sigma \; 2\; \cdots \; an,\; \sigma \; n.\; \{\backslash \; displaystyle\; a\_\; \{1,\; \backslash \; sigma\; \_\; \{1\}\}\; \backslash \; cdot\; a\_\; \{2,\; \backslash \; sigma\; \_\; \{2\}\}\; \backslash \; cdots\; a\_\; \{n,\; \backslash \; sigma\; \_\; \{n\}\}.\}$

Например, определитель матрицы A 3 × 3 (n = 3) равно

$∑ σ ∈ S n sign ⁡ (σ) ∏ i = 1 nai, σ i = sgn ⁡ ([1, 2, 3]) ∏ i = 1 nai, [1, 2, 3] i + sgn ⁡ ([1, 3, 2]) ∏ i = 1 nai, [1, 3, 2] i + sgn ⁡ ([2, 1, 3]) ∏ i = 1 nai, [2, 1, 3] i + sgn ⁡ ([2, 3, 1]) ∏ i = 1 nai, [2, 3, 1] i + sgn ⁡ ([3, 1, 2]) ∏ i = 1 nai, [3, 1, 2] i + sgn ⁡ ([3, 2, 1]) ∏ i = 1 nai, [3, 2, 1] i = ∏ i = 1 nai, [1, 2, 3] i - ∏ i = 1 nai, [1, 3, 2] i - ∏ i = 1 nai, [2, 1, 3] i + ∏ i = 1 nai, [2, 3, 1] i + ∏ i = 1 nai, [3, 1, 2] i - ∏ i = 1 nai, [3, 2, 1] i = a 1, 1 a 2, 2 a 3, 3 - a 1, 1 a 2, 3 a 3, 2 - а 1, 2 а 2, 1 а 3, 3 + а 1, 2 а 2, 3 а 3, 1 + а 1, 3 а 2, 1 а 3, 2 - а 1, 3 а 2, 2 а 3, 1. {\ displaystyle {\ begin {align} \ sum _ {\ sigma \ in S_ {n}} \ operatorname {sgn} (\ sigma) \ prod _ {i = 1} ^ {n} a_ {i, \ sigma _ {i}} \\ = {} \ operatorname {sgn} ([1,2,3]) \ prod _ {i = 1} ^ {n} a_ {i, [1,2, 3] _ {i}} + \ operatorname {sgn} ([1,3,2]) \ prod _ {i = 1} ^ {n} a_ {i, [1,3,2] _ {i}} + \ operatorname {sgn} ([ 2,1,3]) \ prod _ {i = 1} ^ {n} a_ {i, [2,1,3] _ {i}} + {} \\ \ operatorname {sgn} ([2, 3,1]) \ prod _ {i = 1} ^ {n} a_ {i, [2,3,1] _ {i}} + \ operatorname {sgn} ([3,1,2]) \ prod _ {i = 1} ^ {n} a_ {i, [3,1,2] _ {i}} + \ operatorname {sgn} ([3,2,1]) \ prod _ {i = 1} ^ {n} a_ {i, [3,2,1] _ {i}} \\ = {} \ prod _ {i = 1} ^ {n} a_ {i, [1,2, 3] _ { i}} - \ prod _ {i = 1} ^ {n} a_ {i, [1,3,2] _ {i}} - \ prod _ {i = 1} ^ {n} a_ {i, [ 2,1,3] _ {i}} + \ prod _ {i = 1} ^ {n} a_ {i, [2,3,1] _ {i}} + \ prod _ {i = 1} ^ {n} a_ {i, [3,1,2] _ {i}} - \ prod _ {i = 1} ^ {n} a_ {i, [3,2,1] _ {i}} \\ [2pt] = {} a_ {1,1} a_ {2,2} a_ {3,3} -a_ {1,1} a_ {2,3} a_ {3,2} -a_ {1,2 } a_ {2,1} a_ {3,3} + a_ {1,2} a_ {2,3} a_ {3,1} + a_ {1,3} a_ {2,1} a_ {3,2 } -a_ {1,3} a_ {2,2} a_ {3,1}. \ End {align}}}$

символ Леви-Чивита

Иногда расширить формула Лейбница к суммированию, в котором не только перестановки, но встречаются все примеры из n индексов в диапазоне 1,..., n, гарантируя, что вкладывать будет равенство нулю, если это не означает перестановку. Таким образом, полностью антисимметричный символ Леви-Чивита $\epsilon \; i\; 1,\; \cdots ,\; в\; \{\backslash \; displaystyle\; \backslash \; varepsilon\; \_\; \{i\_\; \{1\},\; \backslash \; cdots,\; i\_\; \{n\}\}\}$ расширяет сигнатуру перестановки, задавая $\epsilon \; \sigma \; (1),\; \cdots ,\; \sigma \; (n)\; =\; sgn\; \; (\sigma )\; \{\backslash \; displaystyle\; \backslash \; varepsilon\; \_\; \{\backslash \; sigma\; (1),\; \backslash \; cdots,\; \backslash \; sigma\; (n)\}\; =\; \backslash \; OperatorName\; \{sgn\}\; (\backslash \; sigma)\}$для любой перестановки σ числа n и $\epsilon \; i\; 1,\; \cdots ,\; in\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; varepsilon\; \_\; \{i\_\; \{1\},\; \backslash \; cdots,\; i\_\; \{n\}\}\; =\; 0\}$, когда не существует перестановки σ такой, что $\sigma \; (j)\; =\; ij\; \{\backslash \; displaystyle\; \backslash \; sigma\; (j)\; =\; i\_\; \{j\}\}$для $j\; =\; 1,\dots ,\; n\; \{\backslash \; displaystyle\; j\; =\; 1,\; \backslash \; ldots,\; n\}$(или, что эквивалентно, когда некоторые пары индексов равны). Определитель для матрицы размера n × n может быть выражен с помощью n-кратного суммирования как

$det\; (A)\; =\; \sum \; i\; 1,\; i\; 2,\dots ,\; in\; =\; 1\; n\; \epsilon \; i\; 1\; \cdots \; ina\; 1,\; i\; 1\; \cdots \; ан,\; в,\; \{\backslash \; displaystyle\; \backslash \; det\; (A)\; =\; \backslash \; sum\; \_\; \{i\_\; \{1\},\; i\_\; \{2\},\; \backslash \; ldots,\; i\_\; \{n\}\; =\; 1\}\; ^\; \{n\}\; \backslash \; varepsilon\; \_\; \{i\_\; \{1\}\; \backslash \; cdots\; i\_\; \{n\}\}\; a\_\; \{1,\; i\_\; \{1\}\}\; \backslash \; cdots\; a\_\; \{n,\; i\_\; \{n\}\},\}$

или с использованием двух символов эпсилон как

$det\; (A)\; =\; 1\; n!\; \sum \; \epsilon \; я\; 1\; \cdots \; в\; \epsilon \; J\; 1\; \cdots \; jnai\; 1\; J\; 1\; \cdots \; ainjn,\; \{\backslash \; displaystyle\; \backslash \; det\; (A)\; =\; \{\backslash \; frac\; \{1\}\; \{n!\}\}\; \backslash \; Sum\; \backslash \; varepsilon\; \_\; \{i\_\; \{1\}\; \backslash \; cdots\; i\_\; \{n\}\}\; \backslash \; varepsilon\; \_\; \{j\_\; \{1\}\; \backslash \; cdots\; j\_\; \{n\}\}\; a\_\; \{i\_\; \{1\}\; j\_\; \{1\}\}\; \backslash \; cdots\; a\_\; \{i\_\; \{n\}\; j\_\; \{n\}\},\}$

где сейчас каждый i r и каждый j r следует суммировать по 1,..., n.

Однако, используя тензорную нотацию и исключительное символическое суммирования (соглашение Эйнштейна о суммировании), мы можем получить гораздо более компактное выражение определителя системы второго порядка $n\; =\; 3\; \{\backslash \; displaystyle\; n\; =\; 3\}$размеры, $anm\; \{\backslash \; displaystyle\; a\_\; \{n\}\; ^\; \{m\}\}$;

$det\; (anm)\; erst\; =\; eijkariasjatk\; \{\backslash \; displaystyle\; \backslash \; det\; (a\_\; \{n\})\; ^\; \{m\})\; e\_\; \{rst\}\; =\; e\_\; \{ijk\}\; a\_\; \{r\}\; ^\; \{i\}\; a\_\; \{s\}\; ^\; \{j\}\; a\_\; \{t\}\; ^\; \{k\}\}$

где $erst\; \{\backslash \; displaystyle\; e\_\; \{rst\}\}$и $eijk\; \{\backslash \; displaystyle\; e\_\; \{ijk\}\}$представить собой «электронные системы», которые принимают значения 0, +1 и -1 с учетом количества перестановок $ijk\; \{\backslash \; displaystyle\; ijk\; \}$и $rst\; \{\backslash \; displaystyle\; rst\}$. Более конкретно, $e\; i\; j\; k\; \{\backslash \; displaystyle\; e\_\; \{ijk\}\}$равно 0, когда есть повторяющийся индекс в $i\; j\; k\; \{\backslash \; displaystyle\; ijk\}$; +1, когда присутствует четное количество перестановок $i\; j\; k\; \{\backslash \; displaystyle\; ijk\}$; −1, когда присутствует нечетное количество перестановок $i\; j\; k\; \{\backslash \; displaystyle\; ijk\}$. Количество индексов, представленных в электронных системах, равно $n\; \{\backslash \; displaystyle\; n\}$и, таким образом, может быть обобщено таким образом.

Определитель имеет много свойств. Некоторые основные свойства определителей:

1. $det\; (I\; n)\; =\; 1\; \{\backslash \; displaystyle\; \backslash \; det\; \backslash \; left\; (I\_\; \{n\}\; \backslash \; right)\; =\; 1\}$, где $I\; n\; \{\backslash \; displaystyle\; I\_\; \{n\}\}$- это $n\; \times \; n\; \{\backslash \; displaystyle\; n\; \backslash \; times\; n\}$единичная матрица.
2. $det\; (AT)\; =\; det\; (A)\; \{\backslash \; displaystyle\; \backslash \; det\; \backslash \; left\; (A\; ^\; \{\backslash \; textf\; \{T\}\}\; \backslash \; right)\; =\; \backslash \; det\; (A)\}$, где $AT\; \{\backslash \; displaystyle\; A\; ^\; \{\backslash \; textf\; \{T\}\}\}$обозначает транспонирование элемента $A\; \{\backslash \; displaystyle\; A\}$.
3. $det\; (A\; -\; 1)\; =\; 1\; det\; (A)\; =\; [det\; (A)]\; -\; 1.\; \{\backslash \; displaystyle\; \backslash \; det\; \backslash \; left\; (A\; ^\; \{-\; 1\}\; \backslash \; right)\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; det\; (A)\}\}\; =\; [\backslash \; det\; (A)]\; ^\; \{-\; 1\}.\}$
4. Для квадратных матриц $A\; \{\backslash \; displaystyle\; A\}$и $B\; \{\backslash \; displaystyle\; B\}$равного размера

   $det\; (AB)\; =\; det\; (A)\; \times \; det\; (B).\; \{\backslash \; Displaystyle\; \backslash \; Det\; (AB)\; =\; \backslash \; Det\; (A)\; \backslash \; раз\; \backslash \; Det\; (B).\}$

5. $Det\; (c\; A)\; =\; cn\; det\; (A)\; \{\backslash \; displaystyle\; \backslash \; det\; (cA)\; =\; c\; ^\; \{n\; \}\; \backslash \; det\; (A)\}$, для $n\; \times \; n\; \{\backslash \; displaystyle\; n\; \backslash \; times\; n\}$матрицы $A\; \{\backslash \; displaystyle\; A\}$.
6. для положительные полуопределенные матрицы $A\; \{\backslash \; displaystyle\; A\}$, $B\; \{\backslash \; displaystyle\; B\}$и $C\; \{\backslash \; displaystyle\; C\}$из равного размера $det\; (A\; +\; B\; +\; C)\; +\; det\; (C)\; \ge \; det\; (A\; +\; C)\; +\; det\; (B\; +\; C)\; \{\backslash \; displaystyle\; \backslash \; det\; (A\; +\; B\; +\; C)\; +\; \backslash \; det\; (C)\; \backslash \; geq\; \backslash \; det\; (A\; +\; C)\; +\; \backslash \; det\; (B\; +\; C)\}$, для $A,\; B,\; C\; \ge \; 0\; \{\backslash \; displaystyle\; A,\; B,\; C\; \backslash \; geq\; 0\}$со следствием $det\; (A\; +\; B)\; \ge \; det\; (A)\; +\; det\; (B).\; \{\backslash \; displaystyle\; \backslash \; det\; (A\; +\; B)\; \backslash \; geq\; \backslash \; det\; (A)\; +\; \backslash \; det\; (B).\}$
7. Если $A\; \{\backslash \; displaystyle\; A\}$- это треугольник матрица, т.е. $aij\; =\; 0\; \{\backslash \; displaystyle\; a\_\; \{ij\}\; =\; 0\}$, всякий раз, когда $i>j\; \{\backslash \; displaystyle\; i>j\}$или, альтернативно, когда его тогда равенство произведению диагональных элементов:

   $det\; (A)\; =\; a\; 11\; a\; 22\; \cdots \; ann\; =\; \prod \; i\; =\; 1\; naii.\; \{\backslash \; displaystyle\; \backslash \; det\; (A)\; =\; a\_\; \{11\}\; a\_\; \{22\}\; \backslash \; cdots\; a\_\; \{nn\}\; =\; \backslash \; prod\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; a\_\; \{ii\}.\}$

Это можно вывести из некоторых свойств, приведенных, но легко это следует использовать из формулы Лейбница (или из разложения Лапласа), в котором тождественная перестановка Единственная, которая дает ненулевой вклад.

Ряд дополнительных свойств относится к влиянию на детерминант изменения конкретных строк или столбцов:

8. Просмотр $n\; \times \; n\; \{\backslash \; displaystyle\; n\; \backslash \; times\; n\}$матрица, состоящая из $n\; \{\backslash \; displaystyle\; n\}$столбцов, о предел является n-линейной функцией. Это означает, что если j-й столбец матрицы $A\; \{\backslash \; displaystyle\; A\}$записан как сумма $aj\; =\; v\; +\; w\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{a\}\; \_\; \{j\}\; =\; \backslash \; mathbf\; \{v\}\; +\; \backslash \; mathbf\; \{w\}\}$из двух векторов-столбцов , все остальные столбцы остаются без изменений, тогда определитель $A\; \{\backslash \; displaystyle\; A\}$- это сумма определителей матриц, полученных из $A\; \{\backslash \; displaystyle\; A\}$заменой j-го столбца на $v\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{v\}\}$(обозначается $A\; v\; \{\backslash \; displaystyle\; A\_\; \{v\}\}$), а затем $w\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{w\}\}$(обозначается $A\; w\; \{\backslash \; displaystyle\; A\_\; \{w\}\}$) (и аналогичное отношение сохраняется при записи столбца как скалярного кратного дня столбца).

   $det\; (A)\; =\; det\; ([a\; 1\; |\dots \; |\; aj\; |\dots \; |\; an])\; =\; det\; ([\dots \; |\; v\; +\; w\; |\dots ])\; =\; det\; ([\dots \; |\; v\; |\dots ])\; +\; det\; (\; [\dots \; |\; W\; |\dots ])\; =\; det\; (A\; v)\; +\; det\; (A\; w)\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; det\; (A)\; =\; \backslash \; det\; ([\backslash \; mathbf\; \{a\}\; \_\; \{1\}\; |\; \backslash \; dots\; |\; \backslash \; mathbf\; \{a\}\; \_\; \{j\}\; |\; \backslash \; dots\; |\; \backslash \; mathbf\; \{a\}\; \_\; \{n\}])\; \backslash \backslash \; =\; \backslash \; det\; ([\backslash \; dots\; |\; \backslash \; mathbf\; \{v\}\; +\; \backslash \; mathbf\; \{w\}\; |\; \backslash \; dots])\; \backslash \backslash \; =\; \backslash \; det\; ([\backslash \; dots\; |\; \backslash \; mathbf\; \{v\}\; |\; \backslash \; dots])\; +\; \backslash \; det\; ([\backslash \; dots\; |\; \backslash \; mathbf\; \{w\}\; |\; \backslash \; dots])\; \backslash \backslash \; =\; \backslash \; det\; \backslash \; left\; (A\_\; \{v\}\; \backslash \; right)\; +\; \backslash \; det\; \backslash \; left\; (A\_\; \{w\}\; \backslash \; right)\; \backslash \; end\; \{align\}\}\}$

9. Если в матрице любая строка или столбец имеет все элементы, равные нулю, то Определитель этой матрицы равен 0.
10. Эта n-линейная функция является формой. Это означает, что каждый столбец матрицы идентичны или в более общем смысле, какой-либо столбец может выражен как линейная комбинация других столбцов (т.е. столбцы образуют линейно зависимый набор), его определитель равно 0.

Свойства 1, 8 и 10, которые все следуют из формулы Лейбница, полностью характеризуют определитель; Другими словами, определитель - это уникальная функция от матриц размера n × n до скаляров, которая n-линейной, чередующейся в столбцах, имеет значение 1 для единичной матрицы (эта характеристика сохраняется, если скаляры взяты даже в любом заданном коммутативном кольцо ). Чтобы увидеть это, расширить определение по полилинейности в столбцах до (огромной) линейной комбинации комбинаций матриц, в которой каждый столбец является стандартным базисным вектором. Эти детерминанты равны либо 0 (по свойству 9), либо ± 1 (по свойствам 1 и 12 ниже), поэтому линейная комбинация дает выражение выше в терминах символов Леви-Чивиты. Хотя эта характеристика менее техническая на вид, она не может полностью заменить формулу Лейбница при определении определителя, поскольку без нее существует подходящая функция неясно. Для матриц над некоммутативными кольцами свойства 8 и 9 несовместимы при n ≥ 2, поэтому в этом случае нет определения хорошего определителя.

Свойство 2 выше подразумевает, что свойства столбцов имеют свои аналоги в терминах строк:

11. Если рассматривать матрицу размера n × n как составленную из n строк, определитель n-линейной функции.
12. Эта n-линейная функция представляет собой переменную форму: всякий раз, когда две строки матрицы идентичны, ее определитель равен 0.
13. При замене любой пары столбцов или строк матрицы ее определитель умножается на -1. Это следует из свойств 8 и 10 (это общее свойство полилинейных отображений). В более общем смысле при любом перестановке строк или столбцов определитель умножается на знак перестановки. Под перестановкой замены подразумевается таблица каждой строки как Ri(эквивалентно каждому столбцу как Ci) и переупорядочение строк (или столбцов) путем Rjи Rk(или Cjи Ck), где j, k - два индекса, выбранных от 1 до n для квадратной матрицы размера n × n.
14. Добавление скалярного кратного одного столбца к другому столбцу не меняет значения определителя. Это является следствием свойств 8 и 10 следующим образом: по свойству 8 определен коэффициент, определяющий матрицы с двумя равными столбцами, причем определитель равен 0 по свойству 10. Аналогичным образом добавляется скалярное кратное единице. Строка к другой строке оставляет детерминант без изменений.

Свойство 5 говорит, что определитель на матрицах n × n однороден степени n. Эти свойства используются для упрощения процедуры упрощения процедуры упрощения процедуры до точки. В частности, для матриц с коэффициентами в поле свойства 13 и 14 маятник для преобразования любой матрицы в треугольную матрицу, определитель задается свойством 7; по сути, это метод исключения Гаусса. Например, определитель

$A\; =\; [-\; 2\; 2\; -\; 3\; -\; 1\; 1\; 3\; 2\; 0\; -\; 1]\; \{\backslash \; displaystyle\; A\; =\; \{\backslash \; begin\; \{bmatrix\}\; -2\; 2\; -3\; \backslash \backslash \; -\; 1\; 1\; 3\; \backslash \; \backslash \; 2\; 0\; -1\; \backslash \; end\; \{bmatrix\}\}\}$

можно вычислить с использованием следующего матриц:

$B\; =\; [-\; 2\; 2\; -\; 3\; 0\; 0\; 4.5\; 2\; 0\; -\; 1],\; C\; =\; [-\; 2\; 2\; -\; 3\; 0\; 0\; 4,5\; 0\; 2\; -\; 4],\; D\; =\; [-\; 2\; 2\; -\; 3\; 0\; 2\; -\; 4\; 0\; 0\; 4,5].\; \{\backslash \; displaystyle\; B\; =\; \{\backslash \; begin\; \{bmatrix\}\; -2\; 2\; -3\; \backslash \backslash \; 0\; 0\; 4.5\; \backslash \backslash \; 2\; 0\; -1\; \backslash \; end\; \{bmatrix\}\},\; \backslash \; quad\; C\; =\; \{\backslash \; begin\; \{bmatrix\}\; -2\; 2\; -3\; \backslash \backslash \; 0\; 0\; 4.\; 5\; \backslash \backslash \; 0\; 2\; -4\; \backslash \; end\; \{bmatrix\}\},\; \backslash \; quad\; D\; =\; \{\backslash \; begin\; \{bmatrix\}\; -2\; 2\; -3\; \backslash \backslash \; 0\; 2\; -4\; \backslash \backslash \; 0\; 0\; 4.5\; \backslash \; end\; \{bmatrix\}\}.\}$

Здесь, B получается из A добавлением −1 / 2 × первой строки ко второй, так что det (A) = det ( Б). C получается из B добавлением первой строки к третьей, так что det (C) = det (B). Наконец, D получается из C заменой второй и третьей строк, так что det (D) = −det (C). Определитель (верхней) треугольной матрицы D является произведением ее элементов на главной диагонали : (−2) · 2 · 4,5 = −18. Следовательно, det (A) = −det (D) = +18.

Дополнение Шура

Следующее равенство выполняется дополнение Шура квадратной матрицы :

Дополнение Шура возникает в результате выполнения блока Исключение Гаусса путем умножения матрицы M справа на блочную нижнюю треугольную матрицу

$L\; =\; [I\; p\; 0\; -\; D\; -\; 1\; CI\; q].\; \{\backslash \; displaystyle\; L\; =\; \{\backslash \; begin\; \{bmatrix\}\; I\_\; \{p\}\; 0\; \backslash \backslash \; -\; D\; ^\; \{-\; 1\}\; C\; I\_\; \{q\}\; \backslash \; end\; \{bmatrix\}\}.\}$

Здесь I p обозначает единичную матрица размера p × p . После умножения на матрицу L в верхнем блоке p × p появляется дополнение Шура. Матрица продукта:

$ML\; =\; [ABCD]\; [I\; p\; 0\; -\; D\; -\; 1\; CI\; q]\; =\; [A\; -\; BD\; -\; 1\; CB\; 0\; D]\; =\; [I\; p\; BD\; -\; 1\; 0\; I\; q]\; [A\; -\; BD\; -\; 1\; C\; 0\; 0\; D].\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; ML\; =\; \{\backslash \; begin\; \{bmatrix\}\; AB\; \backslash \backslash \; CD\; \backslash \; end\; \{bmatrix\}\}\; \{\backslash \; begin\; \{bmatrix\}\; I\_\; \{p\}\; 0\; \backslash \backslash \; -\; D\; ^\; \{-\; 1\}\; C\; I\_\; \{q\}\; \backslash \; end\; \{bmatrix\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; A-BD\; ^\; \{-\; 1\}\; CB\; \backslash \backslash \; 0\; D\; \backslash \; end\; \{bmatrix\}\}\; \backslash \backslash \; [5pt]\; =\; \{\backslash \; begin\; \{bmatrix\}\; I\_\; \{p\}\; BD\; ^\; \{-\; 1\}\; \backslash \backslash \; 0\; I\_\; \{q\}\; \backslash \; end\; \{bmatrix\}\}\; \{\backslash \; begin\; \{bmatrix\}\; A-BD\; ^\; \{-\; 1\}\; C\; 0\; \backslash \backslash \; 0\; D\; \backslash \; end\; \{bmatrix\}\}.\; \backslash \; end\; \{выровнено\; \}\}\}$

То есть мы выполнили разложение по Гауссу

$[ABCD]\; =\; [I\; p\; BD\; -\; 1\; 0\; I\; q]\; [A\; -\; BD\; -\; 1\; C\; 0\; 0\; D]\; [I\; p\; 0\; D\; -\; 1\; CI\; q].\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{bmatrix\}\; AB\; \backslash \backslash \; CD\; \backslash \; end\; \{bmatrix\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; I\_\; \{p\}\; BD\; ^\; \{-\; 1\}\; \backslash \backslash \; 0\; I\_\; \{q\}\; \backslash \; end\; \{bmatrix\}\}\; \{\backslash \; begin\; \{bmatrix\}\; A-BD\; ^\; \{-\; 1\}\; C\; 0\; \backslash \backslash \; 0\; D\; \backslash \; end\; \{bmatrix\}\}\; \{\backslash \; begin\; \{bmatrix\}\; I\_\; \{p\}\; 0\; \backslash \backslash \; D\; ^\; \{-\; 1\}\; C\; I\_\; \{q\}\; \backslash \; end\; \{bmatrix\}\; \}.\}$

Первая и последняя матрицы на правой стороне имеют детерминант, равный единице, поэтому мы имеем

$det\; [ABCD]\; =\; det\; (D)\; \cdot \; det\; (A\; -\; BD\; -\; 1\; C).\; \{\backslash \; displaystyle\; \backslash \; det\; \{\backslash \; begin\; \{bmatrix\}\; AB\; \backslash \backslash \; CD\; \backslash \; end\; \{bmatrix\}\}\; =\; \backslash \; det\; (D)\; \backslash \; cdot\; \backslash \; det\; \backslash \; left\; (A-BD\; ^\; \{-\; 1\}\; C\; \backslash \; right).\}$

Это детерминантная личность Шура.

Мультипликативность и группы матриц

Определитель матричного произведения квадратных матриц равен произведению их определителей:

$det\; (AB)\; =\; det\; (A)\; \times \; det\; (B)\; \{\backslash \; displaystyle\; \backslash \; det\; (AB)\; =\; \backslash \; det\; (A)\; \backslash \; times\; \backslash \; det\; (B)\}$

Таким образом, определитель является мультипликативным отображением. Это свойство является следствием приведенной выше характеристики определителя как единственной n-линейной переменной функции столбцов со значением 1 на единичной матрице, поскольку функция M n (K) → K, которая отображает M ↦ det (AM) можно легко увидеть как n-линейный, чередующийся в столбцах M и принимающий значение det (A) в единице. Формула может быть обобщена на (квадратные) произведения прямоугольных матриц, давая формулу Коши – Бине, которая также обеспечивает независимое доказательство мультипликативного свойства.

Определитель det (A) матрицы A отличен от нуля тогда и только тогда, когда A обратима, или, еще один эквивалентный оператор, если его ранг равен размеру матрицы. Если это так, определитель обратной матрицы определяется как

$det\; (A\; -\; 1)\; =\; 1\; det\; (A)\; =\; [det\; (A)]\; -\; 1\; \{\backslash \; displaystyle\; \backslash \; det\; \backslash \; left\; (A\; ^\; \{-\; 1\}\; \backslash \; right)\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; det\; (A)\}\}\; =\; [\backslash \; det\; (A)]\; ^\; \{-\; 1\}\}$

В частности, произведения и обратные матрицы матриц с определителем единица все еще обладают этим свойством. Таким образом, набор таких матриц (фиксированного размера n) образует группу, известную как специальная линейная группа . В более общем смысле, слово «специальный» указывает подгруппу другой группы матриц матриц детерминантной. Примеры включают специальную ортогональную группу (которая, если n равно 2 или 3, состоит из всех матриц вращения ), и специальную унитарную группу .

расширение Лапласа и сопряженная матрица

разложение Лапласа выражает определитель матрицы в терминах ее миноров. Минорный M i, j определяется как определитель (n-1) × (n-1) -матрицы, которая получается из A путем удаления i-й строки и j-го столбца. Выражение (-1) M i, j известно как кофактор. Для каждого i выполнено равенство

$det\; (A)\; =\; \sum \; j\; =\; 1\; n\; (-\; 1)\; i\; +\; jaij\; M\; ij,\; \{\backslash \; displaystyle\; \backslash \; det\; (A)\; =\; \backslash \; sum\; \_\; \{j\; =\; 1\}\; ^\; \{n\}\; (\; -\; 1)\; ^\; \{i\; +\; j\}\; a\_\; \{ij\}\; M\_\; \{ij\},\}$

которое называется разложением Лапласа по i-й строке. Аналогично, разложение Лапласа по j-му столбцу представляет собой равенство

$det\; (A)\; =\; \sum \; i\; =\; 1\; n\; (-\; 1)\; i\; +\; j\; a\; i\; j\; M\; i\; j.\; \{\backslash \; displaystyle\; \backslash \; det\; (A)\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; (-\; 1)\; ^\; \{i\; +\; j\}\; a\_\; \{ij\}\; M\_\; \{ij\}.\}$

Например, расширение Лапласа матрицы 3 × 3

$A\; =\; [-\; 2\; 2\; -\; 3\; -\; 1\; 1\; 3\; 2\; 0\; -\; 1],\; \{\backslash \; displaystyle\; A\; =\; \{\backslash \; begin\; \{bmatrix\}\; -2\; 2\; -3\; \backslash \backslash \; -\; 1\; 1\; 3\; \backslash \; \backslash \; 2\; 0\; -\; 1\; \backslash \; end\; \{bmatrix\}\},\}$

вдоль второго столбца (j = 2, сумма проходит по i) определяется как,

$det\; (A)\; =\; (-\; 1)\; 1\; +\; 2\; \cdot \; 2\; \cdot \; |\; -\; 1\; 3\; 2\; -\; 1\; |\; +\; (-\; 1)\; 2\; +\; 2\; \cdot \; 1\; \cdot \; |\; -\; 2\; -\; 3\; 2\; -\; 1\; |\; +\; (-\; 1)\; 3\; +\; 2\; \cdot \; 0\; \cdot \; |\; -\; 2\; -\; 3\; -\; 1\; 3\; |\; =\; (-\; 2)\; \cdot \; ((-\; 1)\; \cdot \; (-\; 1)\; -\; 2\; \cdot \; 3)\; +\; 1\; \cdot \; ((-\; 2)\; \cdot \; (-\; 1)\; -\; 2\; \cdot \; (-\; 3))\; =\; (-\; 2)\; \cdot \; (-\; 5)\; +\; 8\; =\; 18.\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; det\; (A)\; =\; (-\; 1)\; ^\; \{1\; +\; 2\}\; \backslash \; cdot\; 2\; \backslash \; cdot\; \{\backslash \; begin\; \{vmatrix\}\; -1\; 3\; \backslash \backslash \; 2\; -\; 1\; \backslash \; end\; \{vmatrix\}\}\; +\; (-\; 1)\; ^\; \{2\; +\; 2\}\; \backslash \; cdot\; 1\; \backslash \; cdot\; \{\backslash \; begin\; \{vmatrix\}\; -2\; -3\; \backslash \backslash \; [4pt]\; 2\; -1\; \backslash \; end\; \{vmatrix\}\}\; +\; (-\; 1)\; ^\; \{3\; +\; 2\}\; \backslash \; cdot\; 0\; \backslash \; cdot\; \{\backslash \; begin\; \{vmatrix\}\; -2\; -3\; \backslash \backslash \; -\; 1\; 3\; \backslash \; end\; \{vmatrix\}\}\; \backslash \backslash \; [4pt]\; =\; (-\; 2)\; \backslash \; cdot\; ((-1)\; \backslash \; cdot\; (-1)\; -2\; \backslash \; cdot\; 3)\; +1\; \backslash \; cdot\; ((-2)\; \backslash \; cdot\; (-1)\; -2\; \backslash \; cdot\; (-3))\; \backslash \backslash \; [\; 4pt]\; =\; (-\; 2)\; \backslash \; cdot\; (-5)\; +\; 8\; =\; 18.\; \backslash \; End\; \{align\}\}\}$

Расширение Лапласа может изменить итеративно для вычислений детерминантов, но это эффективно для маленьких только матриц и разреженных матриц, поскольку для общих матриц это требует вычислений экспоненциального числа детерминантов, если позаботятся о том, чтобы вычислить каждый младший только один раз. сопряженная матрица adj (A) является транспонированной матрицей кофакторов, то есть

$(adj\; \; (A))\; i\; j\; =\; (-\; 1)\; i\; +\; j\; M\; j\; i.\; \{\backslash \; displaystyle\; (\backslash \; operatorname\; \{adj\}\; (A))\; \_\; \{ij\}\; =\; (-\; 1)\; ^\; \{i\; +\; j\}\; M\_\; \{ji\}.\}$

Для каждой матрицы есть

$(det\; A)\; I\; =\; A\; прил\; \; A\; =\; (прил\; \; A)\; A.\; \{\backslash \; displaystyle\; (\backslash \; det\; A)\; I\; =\; A\; \backslash \; operatorname\; \{adj\}\; A\; =\; (\backslash \; operatorname\; \{adj\}\; A)\; \backslash ,\; A.\}$

Таким образом, матрица сопряженных элементов может быть установка для обозначения, обратного невырожденная матрица :

$A\; -\; 1\; =\; 1\; det\; A\; adj\; \; A.\; \{\backslash \; displaystyle\; A\; ^\; \{-\; 1\}\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; det\; A\}\}\; \backslash \; operatorname\; \{adj\}\; A.\}$

Теорема Сильвестра о детерминанте

Теорема Сильвестра утверждает, что для A, матрица размером m × n, а B - матрица размера n × m (так что A и B имеют размеры, позволяющие их умножать в любом порядке, образуя квадратную матрицу):

$det\; (I\; m\; +\; AB)\; =\; det\; (I\; п\; +\; ВА),\; \{\backslash \; Displaystyle\; \backslash \; det\; \backslash \; left\; (I\; \_\; \{\backslash \; mathit\; \{m\}\}\; +\; AB\; \backslash \; right)\; =\; \backslash \; det\; \backslash \; left\; (I\; \_\; \{\backslash \; mathit\; \{n\}\}\; +\; BA\; \backslash \; right),\}$

где I m и I n - это единичные матрицы размером m × m и n × n, соответственно.

Из этого общего результата следует несколько следствий.

1. Для случая вектор-столбца c и вектор-строки, каждый из m компонентов, формула позволяет быстро вычислить определитель матрицы, который отличается от единичной матрицы матрицей ранга 1:

   $det\; (I\; m\; +\; cr)\; =\; 1\; +\; rc.\; \{\backslash \; displaystyle\; \backslash \; det\; \backslash \; left\; (I\; \_\; \{\backslash \; mathit\; \{m\}\}\; +\; cr\; \backslash \; right)\; =\; 1\; +\; rc.\}$

2. В общем, для любой обратимой матрицы X размера m × m
   $det\; (Икс\; +\; AB)\; знак\; равно\; Det\; (Икс)\; Det\; (IN\; +\; BX\; -\; 1\; A),\; \{\backslash \; Displaystyle\; \backslash \; Det\; (X\; +\; AB)\; =\; \backslash \; Det\; (X)\; \backslash \; det\; \backslash \; left\; (I\; \_\; \{\backslash \; mathit\; \{n\}))\}\; +\; BX\; ^\; \{-\; 1\}\; A\; \backslash \; right),\}$
3. Для вектора столбца и строки, как указано выше:
   $det\; (X\; +\; cr)\; =\; det\; (X)\; det\; (1\; +\; r\; X\; -\; 1\; c)\; =\; det\; (X)\; +\; r\; прил\; \; (X)\; c.\; \{\backslash \; displaystyle\; \backslash \; det\; (X\; +\; cr)\; =\; \backslash \; det\; (X)\; \backslash \; det\; \backslash \; left\; (1\; +\; rX\; ^\; \{-\; 1\}\; c\; \backslash \; right)\; =\; \backslash \; det\; (X)\; +\; r\; \backslash ,\; \backslash \; operatorname\; \{adj\}\; (X)\; \backslash ,\; c.\}$
4. Для квадратных матриц $A\; \{\backslash \; displaystyle\; A\}$и $B\; \{\backslash \; displaystyle\; B\}$одинакового размера матрицы $AB\; \{\backslash \; displaystyle\; AB\}$и $BA\; \{\backslash \; displaystyle\; BA\}$имеют одинаковые характеристики многочлены (следовательно, одинаковые собственные значения).

Отношение к собственным значениям и следу

Пусть A - произвольная матрица комплексных чисел размера n × n с собственными значениями $\lambda \; 1,\; \lambda \; 2,\dots ,\; \Lambda \; n\; \{\backslash \; displaystyle\; \backslash \; lambda\; \_\; \{1\},\; \backslash \; lambda\; \_\; \{2\},\; \backslash \; ldots,\; \backslash \; lambda\; \_\; \{n\}\}$. (Здесь подразумевается, что собственное значение с алгебраическойностью μ встречается в этом списке μ раз.) Определитель A является произведением всех собственных значений,

$det\; (A)\; =\; \prod \; i\; =\; 1\; п\; \lambda \; я\; знак\; равно\; \lambda \; 1\; \lambda \; 2\; \lambda \; п.\; \{\backslash \; displaystyle\; \backslash \; det\; (A)\; =\; \backslash \; prod\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; \backslash \; lambda\; \_\; \{i\}\; =\; \backslash \; lambda\; \_\; \{1\}\; \backslash \; lambda\; \_\; \{2\}\; \backslash \; cdots\; \backslash \; lambda\; \_\; \{n\}.\}$

Произведение всех ненулевых регистрируется как псевдодетерминант.

И наоборот, детерминанты могут использовать для поиска собственные значения матрицы A: они являются решениями характеристическое значение

$det\; (A\; -\; \lambda \; I)\; =\; 0,\; \{\backslash \; displaystyle\; \backslash \; det\; (A-\; \backslash \; lambda\; I)\; =\; 0\; ~,\}$

где I - единичная матрица той же размерности, что и A, а λ - (скалярное) число, которое решает уравнение (существует не более n решений, где n - размерность A).

A Эрмитова матрица является положительно определенным, если все ее собственные значения положительны. Критерий Сильвестра утверждает, что это эквивалентно определителям подматриц

$A\; k:\; =\; [a\; 1,\; 1\; a\; 1,\; 2\dots \; a\; 1,\; ka\; 2,\; 1\; a\; 2,\; 2\dots \; a\; 2,\; k\; ⋮\; ⋮\; \ddots \; ⋮\; ак,\; 1\; ак,\; 2\dots \; ак,\; к].\; \{\backslash \; displaystyle\; A\_\; \{k\}:\; =\; \{\backslash \; begin\; \{bmatrix\}\; a\_\; \{1,1\}\; a\_\; \{1,2\}\; \backslash \; dots\; a\_\; \{1,\; k\}\; \backslash \backslash \; a\_\; \{2,1\}\; и\; a\_\; \{2,\; 2\}\; \backslash \; dots\; a\_\; \{2,\; k\}\; \backslash \backslash \backslash \; vdots\; \backslash \; vdots\; \backslash \; ddots\; \backslash \; vdots\; \backslash \backslash \; a\_\; \{k,\; 1\}\; a\_\; \{k,\; 2\}\; \backslash \; dots\; a\_\; \{k,\; k\; \}\; \backslash \; end\; \{bmatrix\}\}.\}$

положительное значение для всех k от 1 до n.

Трасса tr (A) по определению является суммой диагональных элементов A, а также равна сумме собственных значений. Таким образом, для комплексных матриц A

$det\; (exp\; \; (A))\; =\; exp\; exp\; (tr\; \; (A))\; \{\backslash \; displaystyle\; \backslash \; det\; (\backslash \; exp\; (A))\; =\; \backslash \; exp\; (\backslash \; Operatorname\; \{tr\}\; (\; A))\}$

или для вещественных матриц A,

$tr\; \; (A)\; =\; log\; \; (det\; (exp\; \; (A))).\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{tr\}\; (A)\; =\; \backslash \; log\; (\backslash \; det\; (\backslash \; exp\; (A))).\}$

Здесь exp (A) обозначает экспоненциальную матрицу число A, потому что каждое собственное значение λ оператора A соответствует собственному значению exp (λ) оператора exp (A). В частности, для любого логарифма числа A, то есть любой матрицы L, удовлетворяющей

$exp\; \; (L)\; =\; A\; \{\backslash \; displaystyle\; \backslash \; exp\; (L)\; =\; A\}$

определителю A задается формулой

$det\; (A)\; =\; exp\; \; (tr\; \; (L)).\; \{\backslash \; displaystyle\; \backslash \; det\; (A)\; =\; \backslash \; exp\; (\backslash \; operatorname\; \{tr\}\; (L)).\}$

Например, для n = 2, n = 3 и n = 4, соответственно,

$det (A) = 1 2 ((tr ⁡ (A)) 2 - tr ⁡ (A 2)), det (A) = 1 6 ((tr ⁡ (A)) 3 - 3 tr ⁡ (A) tr ⁡ (A 2) + 2 tr ⁡ (A 3)), det (A) = 1 24 ((tr ⁡ (A)) 4-6 tr ⁡ (A 2) (tr ⁡ (A)) 2 + 3 (tr ⁡ (A 2)) 2 + 8 tr ⁡ (A 3) tr ⁡ (A) - 6 tr ⁡ (A 4)). {\ Displaystyle {\ begin {align} \ det (A) = {\ frac {1} {2}} \ left (\ left (\ operatorname {tr} (A) \ right) ^ {2} - \ operatorname {tr} \ left (A ^ {2} \ right) \ right), \\\ det (A) = {\ frac {1} {6}} \ left (\ left (\ operatorname {tr} (A) \ right) ^ {3} -3 \ operatorname {tr} (A) ~ \ operatorname {tr} \ left (A ^ {2} \ right) +2 \ operatorname {tr} \ left (A ^ {3} \ right) \ right), \\\ det (A) = {\ frac {1} {24}} \ left (\ left (\ operatorname {tr} (A) \ right) ^ {4} -6 \ имя оператора {tr} \ left (A ^ {2} \ right) \ left (\ operatorname {tr} (A) \ right) ^ {2} +3 \ left (\ operatorname {tr} \ left (A ^ { 2} \ right) \ right) ^ {2} +8 \ operatorname {tr} \ left (A ^ {3} \ right) ~ \ operatorname {tr} (A) -6 \ operatorname {tr} \ left (A ^ {4} \ right) \ right). \ End {align}}}$

ср. Теорема Кэли-Гамильтона. Такие выражения выводятся из комбинаторных аргументов, тождеств Ньютона или алгоритма Фаддеева - Леверье. То есть для общего n, detA = (-1) c 0 постоянный член со знакомого многочлена , определяемый рекурсивно из

$c\; n\; =\; 1;\; c\; n\; -\; m\; знак\; равно\; -\; 1\; m\; \sum \; k\; знак\; равно\; 1\; m\; c\; n\; -\; m\; +\; k\; tr\; \; (A\; k)\; (1\; \le \; m\; \le \; n).\; \{\backslash \; displaystyle\; c\_\; \{n\}\; =\; 1;\; ~~~\; c\_\; \{nm\}\; =\; -\; \{\backslash \; frac\; \{1\}\; \{m\}\}\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{m\}\; c\_\; \{nm\; +\; k\}\; \backslash \; имя\; оператора\; \{tr\}\; \backslash \; left\; (A\; ^\; \{k\; \}\; \backslash \; right)\; ~~\; (1\; \backslash \; leq\; m\; \backslash \; leq\; n)\; ~.\}$

В общем случае это также можно получить из

$det\; (A)\; =\; \sum \; k\; 1,\; k\; 2,\dots ,\; kn\; \ge \; 0\; k\; 1\; +\; 2\; К\; 2\; +\; \cdots \; +\; nkn\; знак\; равно\; N\; \prod \; l\; знак\; равно\; 1\; N\; (-\; 1)\; kl\; +\; 1\; lklkl!\; тр\; \; (A\; l)\; kl,\; \{\backslash \; displaystyle\; \backslash \; det\; (A)\; =\; \backslash \; sum\; \_\; \{\backslash \; begin\; \{array\}\; \{c\}\; k\_\; \{1\},\; k\_\; \{2\},\; \backslash \; ldots,\; k\_\; \{n\}\; \backslash \; geq\; 0\; \backslash \; \backslash \; k\_\; \{1\}\; +\; 2k\_\; \{2\}\; +\; \backslash \; cdots\; +\; nk\_\; \{n\}\; =\; n\; \backslash \; end\; \{array\}\}\; \backslash \; prod\; \_\; \{l\; =\; 1\}\; ^\; \{n\}\; \{\backslash \; frac\; \{(-1)\; ^\; \{k\_\; \{\; l\}\; +1\}\}\; \{l\; ^\; \{k\_\; \{l\}\}\; k\_\; \{l\}!\}\}\; \backslash \; operatorname\; \{tr\}\; \backslash \; left\; (A\; ^\; \{l\}\; \backslash \; right)\; ^\; \{k\_\; \{l\}\},\}$

где сумма берется по набору всех целых чисел k l ≥ 0, удовлетворяющих уравнению

$\sum \; l\; =\; 1\; nlkl\; =\; n.\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{l\; =\; 1\}\; ^\; \{n\}\; lk\_\; \{l\}\; =\; n.\}$

Формула может быть выражена через полный экспоненциальный полином Белла от n аргументов s l = - (l - 1)! tr (A) как

$det\; (A)\; =\; (-\; 1)\; n\; n!\; B\; n\; (s\; 1,\; s\; 2,\dots ,\; s\; n).\; \{\backslash \; displaystyle\; \backslash \; det\; (A)\; =\; \{\backslash \; frac\; \{(-1)\; ^\; \{n\}\}\; \{n!\}\}\; B\_\; \{n\}\; (s\_\; \{1\},\; s\_\; \{2\},\; \backslash \; ldots,\; s\_\; \{n\}).\}$

Эту формулу также можно использовать для нахождения определителя матрицы A J с многомерными индексами I = (i 1, i 2,..., i r) и J = (j 1, j 2,..., j r). Произведение и след таких матриц естественным образом определяется как

$(AB)\; JI\; =\; \sum \; KAKIBJK,\; tr\; \; (A)\; =\; \sum \; IAI\; I.\; \{\backslash \; displaystyle\; (AB)\; \_\; \{J\}\; ^\; \{I\}\; =\; \backslash \; sum\; \_\; \{K\; \}\; A\_\; \{K\}\; ^\; \{I\}\; B\_\; \{J\}\; ^\; \{K\},\; \backslash \; operatorname\; \{tr\}\; (A)\; =\; \backslash \; sum\; \_\; \{I\}\; A\_\; \{I\}\; ^\; \{I\}.\}$

Важное тождество произвольного измерения n может быть получено из ряда Меркатора разложения логарифма, когда разложение сходится. Если каждое собственное значение матрицы A меньше 1 по модулю,

$det\; (I\; +\; A)\; =\; \sum \; k\; =\; 0\; \infty \; 1\; k!\; (-\; \sum \; J\; знак\; равно\; 1\; \infty \; (-\; 1)\; JJ\; тр\; \; (AJ))\; К,\; \{\backslash \; Displaystyle\; \backslash \; Det\; (I\; +\; A)\; =\; \backslash \; сумма\; \_\; \{к\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; гидроразрыва\; \{1\; \}\; \{k!\}\}\; \backslash \; left\; (-\; \backslash \; sum\; \_\; \{j\; =\; 1\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{(-1)\; ^\; \{j\}\}\; \{j\}\}\; \backslash \; operatorname\; \{tr\}\; \backslash \; left\; (A\; ^\; \{j\}\; \backslash \; right)\; \backslash \; right)\; ^\; \{k\}\; \backslash ,,\}$

где I - единичная матрица. В более общем случае, если

$\sum \; k\; =\; 0\; \infty \; 1\; k!\; (-\; \sum \; j\; знак\; равно\; 1\; \infty \; (-\; 1)\; jsjj\; тр\; \; (A\; j))\; к,\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{1\}\; \{k!\}\}\; \backslash \; Left\; (-\; \backslash \; sum\; \_\; \{j\; =\; 1\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{(-1)\; ^\; \{j\}\; s\; ^\; \{j\}\}\; \{j\}\}\; \backslash \; operatorname\; \{tr\}\; \backslash \; left\; (A\; ^\; \{j\; \}\; \backslash \; right)\; \backslash \; right)\; ^\; \{k\}\; \backslash ,,\}$

раскладывается в виде формального степенного ряда по s, тогда все коэффициенты s при m>n равны нулю, оставшийся многочлен - det (I + sA).

Верхняя и верхняя границы

Для положительно определенной матрицы A оператор трассировки дает дополнительную жесткую нижнюю и верхнюю границы для определения жестких границ

$tr\; \; (I\; -\; A\; -\; 1)\; \le \; журнал\; \; det\; (\; A)\; \le \; тр\; \; (A\; -\; I)\; \{\backslash \; Displaystyle\; \backslash \; OperatorName\; \{tr\}\; \backslash \; left\; (IA\; ^\; \{-\; 1\}\; \backslash \; right)\; \backslash \; Leq\; \backslash \; log\; \backslash \; det\; (A)\; \backslash \; Leq\; \backslash \; OperatorName\; \{tr\}\; (AI)\}$

с равенством тогда и только тогда, когда A = I. Это соотношение может быть получено с помощью формулы для KL-дивергенции между двумя многомерными норм распределениями.

Кроме того,

$n\; tr\; \; (A\; -\; 1)\; \le \; det\; (A)\; 1\; n\; \le \; 1\; n\; tr\; \; (A)\; \le \; 1\; n\; tr\; \; (A\; 2).\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{n\}\; \{\backslash \; operatorname\; \{tr\}\; (A\; ^\; \{-\; 1\})\}\}\; \backslash \; leq\; \backslash \; det\; (A)\; ^\; \{\backslash \; frac\; \{1\}\; \{n\}\}\; \backslash \; leq\; \{\backslash \; frac\; \{1\; \}\; \{n\}\}\; \backslash \; operatorname\; \{tr\}\; (A)\; \backslash \; leq\; \{\backslash \; sqrt\; \{\{\backslash \; frac\; \{1\}\; \{n\}\}\; \backslash \; operatorname\; \{tr\}\; \backslash \; left\; (A\; ^\; \{2\}\; \backslash \; right)\}\}.\}$

Эти неравенства можно доказать, приведя матрицу A к диагональному виду. Как таковые, они отличаются хорошо известный факт, что среднее арифметическое меньше, чем среднее геометрическое, которое меньше, чем среднее арифметическое, т. Е. в свою очередь, меньше среднеквадратичного значения.

правила Крамера

Для матричного уравнения

$A\; x\; =\; b\; \{\backslash \; displaystyle\; Ax\; =\; b\}$, учитывая, что A имеет ненулевой определитель,

решение дается правил Крамера :

$xi\; =\; det\; (A\; i)\; det\; (A)\; i\; =\; 1,\; 2,\; 3,\dots ,\; n\; \{\backslash \; displaystyle\; x\_\; \{i\}\; =\; \{\backslash \; frac\; \{\; \backslash \; det\; (A\_\; \{i\})\}\; \{\backslash \; det\; (A)\}\}\; \backslash \; qquad\; i\; =\; 1,2,3,\; \backslash \; ldots,\; n\}$

где A i матрица, образованная заменой i- го столбца матрицы вектор-столбцом b. Это следует сразу же путем раскрытия определителя по столбцам, т.е.

$det\; (A\; i)\; =\; det\; [a\; 1,\dots ,\; b,\dots ,\; an]\; =\; \sum \; j\; =\; 1\; nxj\; det\; [a\; 1,\dots ,\; ai\; -\; 1,\; aj,\; ai\; +\; 1,\dots ,\; an]\; =\; xi\; det\; (A)\; \{\backslash \; displaystyle\; \backslash \; det\; (A\_\; \{i\})\; =\; \backslash \; det\; \{\backslash \; begin\; \{bmatrix\}\; a\_\; \{1\},\; \backslash \; ldots,\; b,\; \backslash \; ldots,\; a\_\; \{n\}\; \backslash \; end\; \{bmatrix\; \}\}\; =\; \backslash \; sum\; \_\; \{j\; =\; 1\}\; ^\; \{n\}\; x\_\; \{j\}\; \backslash \; det\; \{\backslash \; begin\; \{bmatrix\}\; a\_\; \{1\},\; \backslash \; ldots,\; a\_\; \{i-1\},\; a\_\; \{j\},\; a\_\; \{i\; +\; 1\},\; \backslash \; ldots,\; a\_\; \{n\}\; \backslash \; end\; \{bmatrix\}\}\; =\; x\_\; \{i\}\; \backslash \; det\; (A)\}$

где конструкция $aj\; \{\backslash \; displaystyle\; a\_\; \{j\}\}$- столбцы A. Правило также подразумевается тождеством

$A\; adj\; \; (A)\; =\; adj\; \; (A)\; A\; =\; det\; (A)\; I\; n.\; \{\backslash \; displaystyle\; A\; \backslash ,\; \backslash \; operatorname\; \{adj\}\; (A)\; =\; \backslash \; operatorname\; \{adj\}\; (A)\; \backslash ,\; A\; =\; \backslash \; det\; (A)\; \backslash ,\; I\_\; \{n\}.\}$

Недавно было показано, что крамеровский правило может быть реализовано за время O (n), что сопоставимо с более распространенными методами решения системных линейных уравнений, такими как LU, QR или разложение по сингулярным значениям.

Блочные матрицы

Предположим A, B, C и D - матрицы размерности n × n, n × m, m × n и m × m соответственно. Тогда

$det\; (A\; 0\; C\; D)\; =\; det\; (A)\; \times \; det\; (D)\; =\; det\; (A\; B\; 0\; D).\; \{\backslash \; displaystyle\; \backslash \; det\; \{\backslash \; begin\; \{pmatrix\}\; A\; 0\; \backslash \backslash \; CD\; \backslash \; end\; \{pmatrix\}\}\; =\; \backslash \; det\; (A)\; \backslash \; times\; \backslash \; det\; (D)\; =\; \backslash \; det\; \{\backslash \; begin\; \{pmatrix\}\; AB\; \backslash \backslash \; 0\; D\; \backslash \; end\; \{pmatrix\}\}.\}$

Это можно увидеть из формулы Лейбница для определителей или из разложения, подобного (для первого случая)

$(A\; 0\; CD)\; =\; (A\; 0\; CI\; m)\; (I\; n\; 0\; 0\; D).\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{pmatrix\}\; A\; 0\; \backslash \backslash \; CD\; \backslash \; end\; \{pmatrix\}\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; A\; 0\; \backslash \backslash \; C\; I\_\; \{m\}\; \backslash \; end\; \{pmatrix\}\}\; \{\backslash \; begin\; \{pmatrix\; \}\; I\_\; \{n\}\; 0\; \backslash \backslash \; 0\; D\; \backslash \; end\; \{pmatrix\}\}.\}$

Если A обратимый, то

$det\; (ABCD)\; =\; det\; (A)\; \times \; det\; (D\; -\; CA\; -\; 1\; Б).\; \{\backslash \; displaystyle\; \backslash \; det\; \{\backslash \; begin\; \{pmatrix\}\; AB\; \backslash \backslash \; CD\; \backslash \; end\; \{pmatrix\}\}\; =\; \backslash \; det\; (A)\; \backslash \; times\; \backslash \; det\; \backslash \; left\; (D-CA\; ^\; \{-\; 1\}\; B\; \backslash \; right).\}$

, что можно увидеть с помощью разложения

$(ABCD)\; =\; (A\; 0\; CI\; m)\; (I\; n\; A\; -\; 1\; B\; 0\; D\; -\; CA\; -\; 1\; B).\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{pmatrix\}\; AB\; \backslash \backslash \; CD\; \backslash \; end\; \{pmatrix\}\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; A\; 0\; \backslash \backslash \; C\; I\_\; \{m\}\; \backslash \; end\; \{pmatrix\}\}\; \{\backslash \; begin\; \{pmatrix\}\; I\_\; \{n\}\; A\; ^\; \{-\; 1\}\; B\; \backslash \backslash \; 0\; D-CA\; ^\; \{-\; 1\}\; B\; \backslash \; end\; \{pmatrix\}\}.\}$

Когда D обратимо, аналогичное тождество с $det\; (D)\; \{\; \backslash \; displaystyle\; \backslash \; det\; (D)\}$исключение может быть получено аналогично, то есть

$det\; (ABCD)\; =\; det\; (D)\; \times \; det\; (A\; -\; BD\; -\; 1\; C).\; \{\backslash \; displaystyle\; \backslash \; det\; \{\backslash \; begin\; \{pmatrix\}\; AB\; \backslash \backslash \; CD\; \backslash \; end\; \{pmatrix\}\}\; =\; \backslash \; det\; (D)\; \backslash \; times\; \backslash \; det\; \backslash \; left\; (A-BD\; ^\; \{-\; 1\}\; C\; \backslash \; right).\}$

Когда блоки представляют собой квадратные матрицы одного порядка, дальнейшие формулы верны. Например, если C и D коммутируют (т. Е. CD = DC), выполняется следующая формула, сравнимая с определителем матрицы 2 × 2:

$det\; (A\; B\; C\; D)\; =\; det\; (A\; D\; -\; B\; C).\; \{\backslash \; displaystyle\; \backslash \; det\; \{\backslash \; begin\; \{pmatrix\}\; AB\; \backslash \backslash \; CD\; \backslash \; end\; \{pmatrix\}\}\; =\; \backslash \; det\; (AD-BC).\}$

Обычно, если все пары матриц размера n × n блока np × np матрица коммутируют, то определитель блочной матрицы равен определителю матрицы, полученной вычислением определителя блочной матрицы, считая ее элементы как элементы матрицы размера p × p. Как показывает предыдущая формула, для p = 2 этого критерия достаточно, но не обязательно.

Когда A = D и B = C, блоки представляют собой квадратные матрицы одного порядка, и выполняется следующая формула (если A и B не коммутируют)

$det\; (ABBA)\; =\; det\; (A\; -\; В)\; \times \; дет\; (А\; +\; В).\; \{\backslash \; displaystyle\; \backslash \; det\; \{\backslash \; begin\; \{pmatrix\}\; AB\; \backslash \backslash \; BA\; \backslash \; end\; \{pmatrix\}\}\; =\; \backslash \; det\; (AB)\; \backslash \; times\; \backslash \; det\; (A\; +\; B).\}$

Когда D является матрицей 1 × 1, B - вектор-столбец, а C - вектор-строка, тогда

$det\; (ABCD)\; =\; (D\; -\; CA\; -\; 1\; B)\; det\; (A).\; \{\backslash \; displaystyle\; \backslash \; det\; \{\backslash \; begin\; \{pmatrix\}\; AB\; \backslash \backslash \; CD\; \backslash \; end\; \{pmatrix\}\}\; =\; \backslash \; left\; (D-CA\; ^\; \{-\; 1\}\; B\; \backslash \; right)\; \backslash \; det\; (A)\; \backslash ,.\}$

Пусть $s\; \{\backslash \; displaystyle\; s\}$- скалярное комплексное число. Если блочная матрица является квадратной, ее характерный многочлен может быть разложен на множители с помощью

$det\; (A\; -\; s\; IBCD\; -\; s\; I)\; =\; det\; (A\; -\; s\; I)\; det\; (D\; -\; C\; adj\; \; (A\; -\; s\; I)\; B\; det\; (A\; -\; s\; I)\; -\; s\; I),\; если\; \notin \; eig\; \; (A)\; =\; det\; (A\; -\; s\; I)\; 1\; -\; n\; -\; m\; det\; (det\; (A\; -\; s\; I)\; D\; -\; C\; прил\; \; (A\; -\; s\; I)\; B\; -\; det\; (A\; -\; s\; I)\; s\; I)\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; det\; \{\backslash \; begin\; \{pmatrix\}\; A-sI\; B\; \backslash \backslash \; C\; D-sI\; \backslash \; конец\; \{pmatrix\}\}\; =\; \backslash \; det\; (A-sI)\; \backslash \; det\; \backslash \; left\; (D\; -\; \{\backslash \; frac\; \{C\; \backslash \; operatorname\; \{adj\}\; (A-sI)\; B\}\; \{\backslash \; det\; (A-sI)\}\}\; -\; sI\; \backslash \; right)\; \backslash \; quad\; \backslash \; mathrm\; \{if\}\; \backslash \; quad\; s\; \backslash \; notin\; \backslash \; operatorname\; \{eig\}\; (A)\; \backslash \backslash \; =\; \backslash \; det\; (A-sI)\; ^\; \{1-nm\}\; \backslash \; det\; \backslash \; left\; (\backslash \; det\; (A-\; sI)\; DC\; \backslash \; operatorname\; \{adj\}\; (A-sI)\; B-\; \backslash \; det\; (A-sI)\; sI\; \backslash \; right)\; \backslash \; end\; \{align\}\}\}$

Производная

Это можно увидеть, например, используя формулу Лейбница, определенная действительная (или аналогичным образом для комплексных) квадратных матриц полиномиальной функции от R до R, и поэтому онвезде дифференцируем. Его производная может быть выражена с помощью формулы Якоби :

$d\; det\; (A)\; d\; \alpha \; =\; tr\; \; (adj\; \; (A)\; d\; A\; d\; \alpha ).\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; \backslash \; det\; (A)\}\; \{d\; \backslash \; alpha\}\}\; =\; \backslash \; operatorname\; \{tr\}\; \backslash \; left\; (\backslash \; operatorname\; \{adj\}\; (A)\; \{\backslash \; frac\; \{dA\}\; \{d\; \backslash \; alpha\}\}\; \backslash \; справа).\}$

где adj (A) обозначает адъюгат к A. В частности, если A обратим, мы имеем

$d\; det\; (A)\; d\; \alpha \; =\; det\; (A)\; tr\; \; (\; A\; -\; 1\; d\; A\; d\; \alpha ).\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; \backslash \; det\; (A)\}\; \{d\; \backslash \; alpha\}\}\; =\; \backslash \; det\; (A)\; \backslash \; operatorname\; \{tr\}\; \backslash \; left\; (A\; ^\; \{-\; 1\}\; \{\backslash \; frac\; \{dA\}\; \{d\; \backslash \; alpha\; \}\}\; \backslash \; right).\}$

Выражаясь в терминах элементов A, это

$\partial \; det\; (A)\; \partial \; A\; ij\; =\; adj\; \; (A)\; ji\; =\; det\; (A)\; (A\; -\; 1)\; ji.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; det\; (A)\}\; \{\backslash \; partial\; A\_\; \{ij\}\}\}\; =\; \backslash \; operatorname\; \{adj\}\; (A)\; \_\; \{ji\}\; =\; \backslash \; det\; (A)\; \backslash \; left\; (A\; ^\; \{-\; 1\}\; \backslash \; right)\; \_\; \{ji\}.\}$

Еще одна эквивалентная формулировка:

$det\; (A\; +\; ϵ\; X)\; -\; det\; (A)\; =\; tr\; \; (adj\; \; (A)\; X)\; ϵ\; +\; O\; (ϵ\; 2)\; знак\; равно\; det\; (A)\; тр\; \; (A\; -\; 1\; Икс)\; ϵ\; +\; O\; (ϵ\; 2)\; \{\backslash \; displaystyle\; \backslash \; det\; (A\; +\; \backslash \; epsilon\; X)\; -\; \backslash \; det\; (A)\; =\; \backslash \; operatorname\; \{tr\}\; (\backslash \; operatorname\; \{прил.\}\; (A)\; X)\; \backslash \; epsilon\; +\; O\; \backslash \; left\; (\backslash \; epsilon\; ^\; \{2\}\; \backslash \; right)\; =\; \backslash \; det\; (A)\; \backslash \; operatorname\; \{tr\}\; \backslash \; left\; (A\; ^\; \{-\; 1\}\; X\; \backslash \; right)\; \backslash \; epsilon\; +\; O\; \backslash \; left\; (\backslash \; epsilon\; ^\; \{2\}\; \backslash \; right)\}$,

с использованием нотации большой буквы O. Особый случай, когда $A\; =\; I\; \{\backslash \; displaystyle\; A\; =\; I\}$, единичная матрица, дает

$det\; (I\; +\; ϵ\; X)\; =\; 1\; +\; tr\; \; (X)\; ϵ\; +\; O\; (\; ϵ\; 2).\; \{\backslash \; displaystyle\; \backslash \; det\; (I\; +\; \backslash \; epsilon\; X)\; =\; 1\; +\; \backslash \; operatorname\; \{tr\}\; (X)\; \backslash \; epsilon\; +\; O\; \backslash \; left\; (\backslash \; epsilon\; ^\; \{2\}\; \backslash \; right).\}$

Этот идентификатор используется при описании касательное пространство типичное группы Ли.

Если матрица A записана как $A\; =\; [abc]\; \{\backslash \; displaystyle\; A\; =\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; mathbf\; \{a\}\; \backslash \; mathbf\; \{\; b\}\; \backslash \; mathbf\; \{c\}\; \backslash \; end\; \{bmatrix\}\}$где a, b, c- технические требования длины 3, тогда градиент по одному из трех векторов может быть записан как векторный произведение двух других:

$\nabla \; a\; det\; (A)\; =\; b\; \times \; c\; \nabla \; b\; det\; (A)\; =\; c\; \times \; a\; \nabla \; c\; det\; (A)\; =\; a\; \times \; b.\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; nabla\; \_\; \{\backslash \; mathbf\; \{a\}\}\; \backslash \; det\; (A)\; =\; \backslash \; mathbf\; \{b\}\; \backslash \; times\; \backslash \; mathbf\; \{c\}\; \backslash \backslash \backslash \; nabla\; \_\; \{\backslash \; mathbf\; \{b\}\}\; \backslash \; det\; (A)\; =\; \backslash \; mathbf\; \{c\}\; \backslash \; times\; \backslash \; mathbf\; \{a\}\; \backslash \backslash \backslash \; nabla\; \_\; \{\backslash \; mathbf\; \{c\}\}\; \backslash \; det\; (A)\; =\; \backslash \; mathbf\; \{a\}\; \backslash \; times\; \backslash \; mathbf\; \{b\}.\; \backslash \; end\; \{align\}\}\}$

Детерминант эндоморфизма

Вышеупомянутые тождества, определенных определителя произведений и обратных матриц, подразумевают, что похожие матрицы имеют один и тот же определитель: две матрицы A и B подобны, если существует обратимая матрица X такая, что A = XBX. Действительно, многократное применение вышеуказанных тождеств дает

$det\; (A)\; =\; det\; (X)\; -\; 1\; det\; (B)\; det\; (X)\; =\; det\; (B)\; det\; (X)\; -\; 1\; det\; (X)\; =\; det\; (B).\; \{\backslash \; Displaystyle\; \backslash \; Det\; (A)\; =\; \backslash \; Det\; (X)\; ^\; \{-\; 1\}\; \backslash \; Det\; (B)\; \backslash \; Det\; (X)\; =\; \backslash \; Det\; (B)\; \backslash \; Det\; (X)\; ^\; \{-\; 1\}\; \backslash \; Det\; (X)\; =\; \backslash \; det\; (B).\}$

Поэтому определитель также называется инвариантом подобия. Определитель линейного преобразования

$T:\; V\; \to \; V\; \{\backslash \; displaystyle\; T:\; V\; \backslash \; rightarrow\; V\}$

для некоторого конечного пространства V определяется как определитель матрицы, описывающей его, относительно произвольного выбора базиса в V. Благодаря инвариантности подобия этот определитель не зависит от выбора базиса для V и, следовательно, зависит только от эндоморфизма T.

Внешняя алгебра

Определитель линейного преобразования T : V → V n-мерного способа пространства V может быть сформулирован безкоординатным образом с учетом n-й внешней степени ΛV из V. индуцирует линейное отображение

$\Lambda \; n\; T:\; \Lambda \; n\; V\; \to \; \Lambda \; n\; V\; v\; 1\; \wedge \; v\; 2\; \wedge \; \cdots \; \wedge \; vn\; \mapsto \; T\; v\; 1\; \wedge \; T\; v\; 2\; \wedge \; \cdots \; \wedge \; T\; vn.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; Lambda\; ^\; \{n\}\; T:\; \backslash \; Lambda\; ^\; \{n\}\; V\; \backslash \; rightarrow\; \backslash \; Lambda\; ^\; \{n\}\; V\; \backslash \backslash \; v\_\; \{1\}\; \backslash \; wedge\; v\_\; \{2\}\; \backslash \; wedge\; \backslash \; dots\; \backslash \; wedge\; v\_\; \{n\}\; \backslash \; mapsto\; Tv\_\; \{1\}\; \backslash \; wedge\; Tv\_\; \{2\}\; \backslash \; wedge\; \backslash \; dots\; \backslash \; wedge\; Tv\_\; \{n\}.\; \backslash \; end\; \{followers\}\}$

оказывается ΛV одномерно, отображение ΛT д умножением на некоторый скаляр. Этот скаляр совпадает с определителем T, то есть есть

$(\Lambda \; n\; T)\; (v\; 1\; \wedge \; \cdots \; \wedge \; v\; n)\; =\; det\; (T)\; \cdot \; v\; 1\; \wedge \; \cdots \; \wedge \; v\; n.\; \{\backslash \; displaystyle\; \backslash \; left\; (\backslash \; Lambda\; ^\; \{n\}\; T\; \backslash \; right)\; \backslash \; left\; (v\_\; \{1\}\; \backslash \; wedge\; \backslash \; dots\; \backslash \; wedge\; v\_\; \{n\}\; \backslash \; right)\; =\; \backslash \; det\; (T)\; \backslash \; cdot\; v\_\; \{1\}\; \backslash \; wedge\; \backslash \; dots\; \backslash \; wedge\; v\_\; \{n\}.\}$

Это определение согласуется с более конкретным определением, зависящим от координат. В частности, для квадрата $n\; \times \; n\; \{\backslash \; displaystyle\; n\; \backslash \; times\; n\}$матрицы A, столбцы которого равны $a\; 1,\dots ,\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{a\_\; \{1\}\},\; \backslash \; ldots,\; \backslash \; mathbf\; \{a\_\; \{n\}\}\}$, его определитель удовлетворяет $a\; 1\; \wedge \; \cdots \; \wedge \; an\; =\; det\; (A)\; \cdot \; e\; 1\; \wedge \; \cdots \; \wedge \; en\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\; a\_\; \{1\}\}\; \backslash \; клин\; \backslash \; точки\; \backslash \; клин\; \backslash \; mathbf\; \{a\_\; \{n\}\}\; =\; \backslash \; det\; (A)\; \backslash \; cdot\; \backslash \; mathbf\; \{e\_\; \{1\}\}\; \backslash \; клин\; \backslash \; точки\; \backslash \; клин\; \backslash \; mathbf\; \{e\_\; \{n\}\}\}$, где $\{e\; 1,\dots ,\; en\}\; \{\backslash \; displaystyle\; \backslash \; \{\backslash \; mathbf\; \{e\_\; \{1\}\},\; \backslash \; dots,\; \backslash \; mathbf\; \{e\_\; \{n\}\}\; \backslash \}\}$- это стандартная основа $R\; n\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{R\}\; ^\; \{n\}\}$. Это следует из приведенной выше характеристик определителя. Например, переключение двух столбцов меняет знак определителя; аналогично, перестановка векторов во внешнем произведении v 1 ∧ v 2 ∧ v 3 ∧... ∧ v n на v 2 ∧ v 1 ∧ v 3 ∧... ∧ v n, скажем, тоже меняет знак.

По этой причине наивысшую ненулевую внешнюю мощность Λ (V) иногда также называют детерминантом V и аналогично для более задействованных объектов, таких как связки или цепочка комплексы векторных пространств. Минорные части матрицы также могут быть преобразованы в эту настройку, рассматривая младшие чередующиеся формы ΛV с k < n.

квадратными матрицами над коммутативными кольцами и абстрактными свойствами

Определитель также можно охарактеризовать как уникальную функцию

$D:\; M\; n\; (K)\; \to \; K\; \{\backslash \; displaystyle\; D:\; M\_\; \{n\}\; (K)\; \backslash \; to\; K\}$

из набора всех матриц размера n × n с записями в поле K в это поле, удовлетворяющих следующим трем параметрам. свойства: во-первых, D является n-линейной функцией : учитывая, что все столбцы A, кроме одного, фиксированы, определитель является линейным в оставшемся столбце, то есть

$D\; (v\; 1,\dots ,\; vi\; -\; 1,\; avi\; +\; bw,\; vi\; +\; 1,\dots ,\; vn)\; =\; a\; D\; (v\; 1,\dots ,\; vi\; -\; 1,\; vi,\; vi\; +\; 1,\dots ,\; vn)\; +\; b\; D\; (v\; 1,\dots ,\; vi\; -\; 1,\; w,\; vi\; +\; 1,\dots ,\; vn)\; \{\backslash \; displaystyle\; D\; (v\_\; \{1\},\; \backslash \; dots,\; v\_\; \{i-1\},\; av\_\; \{i\}\; +\; bw,\; v\_\; \{i\; +\; 1\},\; \backslash \; dots,\; v\_\; \{n\; \})\; =\; aD\; (v\_\; \{1\},\; \backslash \; dots,\; v\_\; \{i-1\},\; v\_\; \{i\},\; v\_\; \{i\; +\; 1\},\; \backslash \; dots,\; v\_\; \{n\})\; +\; bD\; (v\_\; \{1\},\; \backslash \; dots,\; v\_\; \{i-1\},\; w,\; v\_\; \{i\; +\; 1\},\; \backslash \; dots,\; v\_\; \{n\})\}$

для любых векторов-столбцов v 1,..., v n, w и любые скаляры (element s из K) a и b. Во-вторых, D является функцией чередования : для любой матрицы A с двумя идентичными столбцами D (A) = 0. Наконец, D (I n) = 1, где I n - единичная матрица.

Этот факт также означает, что для любой другой n-линейной альтернированной функции F: M n (K) → K выполняется

$F\; (M)\; =\; F\; (I)\; D\; (M).\; \{\backslash \; displaystyle\; F\; (M)\; =\; F\; (I)\; D\; (M).\}$

Это определение также может быть расширено, если K - коммутативное кольцо R, и в этом случае матрица обратима, если и только если ее определитель является обратимым элементом в R. Например, матрица A с элементами в Z, целые числа, является обратимой (в том смысле, что существует обратная матрица с целочисленные записи), если определитель равен +1 или -1. Такая матрица называется унимодулярной.

Определитель определяет отображение

$GL\; n\; \; (R)\; \to \; R\; \times ,\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{GL\}\; \_\; \{n\}\; (R)\; \backslash \; rightarrow\; R\; ^\; \{\; \backslash \; times\},\}$

между группой обратимых матриц размера n × n с элементами в R и мультипликативной группой единиц в R. Поскольку она учитывает умножение в обеих группах, это отображение является гомоморфизм групп. Во-вторых, для гомоморфизма кольца f: R → S существует отображение GL n (f): GL n (R) → GL n (S), заданное заменой всех записей в R их изображениями под f. Определитель учитывает эти отображения, т. Е. Для матрицы A = (a i, j) с элементами в Rтождество

$е\; (det\; ((ai,\; j)))\; =\; det\; ((е\; (ai,\; j)))\; \{\backslash \; displaystyle\; f\; (\backslash \; det\; ((a\_\; \{i,\; j\})))\; =\; \backslash \; det\; ((\; f\; (a\_\; \{i,\; j\})))\}$

. Другими словами, следующая диаграмма коммутирует:

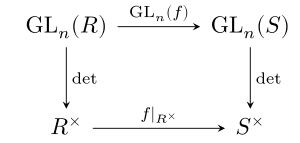
, определитель комплексно-сопряженной комплексной матрицы (которая также является определителем ее сопряженного транспонирования) комплексно-сопряженным ее определителем, и для целочисленных матриц: редукция по модулю m определителя такая матрица равна определителю матрицы, приведенной по модулю m (последний определитель вычисляется с использованием модульной арифметики ). На языке теории категорий определитель - это естественное преобразование между двумя функторами GL n и (⋅) (см. Также Естественное преобразование # Определитель ). Добавляя еще один уровень абстракции, это фиксируется утверждением, что определено является морфизмом алгебраических групп, от общей линейной группы к мультипликативной группе,

$det:\; GL\; n\; \to \; G\; m.\; \{\backslash \; displaystyle\; \backslash \; det:\; \backslash \; operatorname\; \{GL\}\; \_\; \{n\}\; \backslash \; rightarrow\; \backslash \; mathbb\; \{G\}\; \_\; \{m\}.\}$

Бесконечные матрицы

Для матриц с бесконечным числом приведенных выше определений рядов и столбцов приведенные выше определения не переносятся напрямую. Например, в формуле Лейбница должна быть вычислена бесконечная сумма (все члены которой имеют бесконечные произведения). Функциональный анализ функции расширения определителя для таких бесконечных операций, которые, однако, работают только для определенных видов операторов.

Детерминант Фредгольма определяет определитель для агентов, известных как операторы класса трассировки, посредством соответствующего обобщения формулы

$det\; (I\; +\; A)\; =\; exp\; \; (tr\; \; (журнал\; \; (I\; +\; A))).\; \{\backslash \; displaystyle\; \backslash \; det\; (I\; +\; A)\; =\; \backslash \; exp\; (\backslash \; operatorname\; \{tr\}\; (\backslash \; log\; (I\; +\; A))).\}$

Еще одно бесконечномерное понятие определителя - это функциональный определитель.

Операторы в алгебрах фон Неймана

Для операторов в конечном множителе можно определить положительный вещественный определитель, называемый определенным Фугледе-Кадисона, используя канонический след. Фактически, каждому следу на алгебре фон Неймана соответствует понятие определителя Фугледе-Кадисона.

Связанные понятия для некоммутативных колец

Для квадратных матриц элементов в некоммутативном кольце существуют трудности при определении аналогично определению для коммутативных колец. Смысл может быть придан формуле Лейбница при условии, что указан порядок продукта, аналогично для других определителей, но некоммутативность приводит к потере многих фундаментальных свойств определителя, таких как мультипликативное свойство или факт, что определитель не меняется при перестановке матрицы. Над некомативными кольцами нет разумного понятия полилинейной формы (существование ненулевой билинейной формы с регулярным элементом R в качестве значения по некоторой паре аргументов означает, что R коммутативна). Тем не менее, были сформулированы различные понятия некоммутативного определителя, которые сохраняют некоторые свойства определителей, в частности квазидетерминанты и определитель Дьедонне. Для некоторых классов матриц с некоммутативными элементами можно определить определитель и доказать теоремы линейной алгебры, которые очень похожи на коммутативные аналоги. Примеры включают q-определитель на квантовых групп, определитель Капелли на матрицах Капелли и березинианский на суперматрицах. Матрицы Манина класс, наиболее близкий к матрицам с коммутативными элементами.

Дополнительные варианты

Детерминанты матриц в суперкольцах (то есть есть Z 2-градуированных кольцах ) известны как березинцы или супердетерминанты.

перманент матрицы определены как детерминант, за исключением того, что факторы sgn (σ), которые возникают в правиле Лейбница, опускаются. Имманант обобщает оба, вводя символ симметрической группы Snв правиле Лейбница.

Детерминанты в основном используются как теоретический инструмент. Они редко вычисляются явно в числовой линейной алгебре, где для таких приложений, как проверка обратимости и поиск других методов, определитель в степени заменен другими методами. Вычислительная геометрия, однако часто использует вычисления соответствующими с определителями.

Наивные методы реализации алгоритма для вычисителя включают использование формулы Лейбница или формулы Лапласа. Однако оба эти подхода крайне неэффективны для больших матриц, поскольку количество требуемых операций растет очень быстро: оно составляет порядка n! (n факториал ) для матрицы размера n × n. Например, формула Лейбница требует вычислений! товары. Поэтому для вычислений были созданы сложные методы детерминантов.

Методы разложения

Для заданной матрицы A некоторые методы вычисляют ее определитель, записывая A как произведение матриц, определители которых вычислить легче. Такие методы называются методы декомпозиции. Примеры включают в себя разложение LU, QR-разложение или разложение Холецкого (для положительно определенных матриц ). Эти методы имеют значительным улучшением по сравнению с O (n!)

Разложение LU выражает A в терминах нижней треугольной матрицы L, верхней треугольной матрицы U и матрица перестановок P:

$A\; =\; PLU.\; \{\backslash \; displaystyle\; A\; =\; PLU.\}$

Определители L и U можно быстро вычислить, поскольку они являются произведениями соответствующих диагональных элементов. Определитель P - это просто знак $\epsilon \; \{\backslash \; displaystyle\; \backslash \; varepsilon\}$получение перестановки (который равен +1 для четного числа перестановок и -1 для нечетного числа перестановок). Тогда определитель A равен

$det\; (A)\; =\; \epsilon \; det\; (L)\; \cdot \; det\; (U).\; \{\backslash \; displaystyle\; \backslash \; det\; (A)\; =\; \backslash \; varepsilon\; \backslash \; det\; (L)\; \backslash \; cdot\; \backslash \; det\; (U).\}$

(см. детерминантные тождества.) Кроме того, разложение можно выбрать так, чтобы L представляет собой унитреугольную матрицу и, следовательно, имеет определитель 1, и в этом случае формула дополнительно упрощается до

$det\; (A)\; =\; \epsilon \; det\; (U).\; \{\backslash \; displaystyle\; \backslash \; det\; (A)\; =\; \backslash \; varepsilon\; \backslash \; det\; (U).\}$

Дополнительные методы

. Определитель A и обратный к A уже вычислены, определитель матрицы лемма позволяет быстро вычислить определитель A + uv, где u и v - тип-столбцы.

Определителя не требует деления, возникает вопрос: существуют ли быстрые алгоритмы, не требующие деления? Это особенно интересно для матриц над кольцами. Действительно, алгоритмы, время выполнения которых существуют алгоритмы. Алгоритм Махаджана, Виная и Берковица основан на (короткометражке). Некоторые из этих продуктов может быть вычислена более эффективно, чем требует определения детерминанта. Окончательный алгоритм очень похож на повторное произведение треугольных матриц.

Если две матрицы порядка n можно перемножить за время M (n), где M (n) ≥ n для некоторого a>2, то определитель можно вычислить за время O (M (n)). Это означает, например, что существует алгоритм O (n) на основе алгоритма Копперсмита - Винограда.

Чарльза Доджсона (т.е. Льюиса Кэрролла из Приключения Алисы в стране чудес fame) изобрел метод вычисления детерминантов, названный конденсацией Доджсона. К сожалению, этот интересный метод не всегда работает в первозданном виде.

Алгоритмы также можно оценивать в соответствии с их битовой сложностью, то есть сколько битов точности необходимо для хранения промежуточных значений, высоких при вычислении. Например, метод исключения Гаусса (или разложение LU) имеет порядок O (n), но длина в битах промежуточных значений может стать экспоненциально длинной. Алгоритм Барейса, с другой стороны, представляет собой метод точного деления, основанный на идентичности Сильвестра также имеет порядок n, но битовая сложность примерно равна размеру битов исходных записей. в матрице, умноженной на n.

Исторически детерминанты использовались задолго до матриц: детерминант был первоначально определен как свойство системы линейных уравнений. Определитель «определяет», есть ли у системы единственное решение (что происходит именно в том случае, если определитель не равен нулю). В этом смысле детерминанты были впервые использованы в китайском учебнике математики Девять глав математического искусства (九章 算術, китайские ученые, примерно в III веке до нашей эры). В Европе детерминанты 2 × 2 рассматривались Кардано в конце XVI века, а более крупные - Лейбницем.

В Японии Секи Такакадзу приписывают открытие результирующей и определителя (сначала в 1683 г., полная версия не позднее 1710 г.). В Европе Крамер (1750) дополнил теорию, рассматривая предмет в отношении системы уравнений. Впервые о законе повторяемости объявил Безу (1764 г.).

Именно Вандермонд (1771) первым признал детерминанты как независимые функции. Лаплас (1772) общий метод расширения детерминанта с точки зрения его дополнительной несовершеннолетние : Вандермонд уже привел особый случай. Сразу после этого Лагранж (1773) рассмотрел детерминанты второго и третьего порядка и применил их к вопросам теории исключения ; он доказал много частных случаев общих тождеств.

Гаусс (1801) сделал следующий шаг вперед. Как и Лагранж, он много использовал детерминанты в теории чисел. Он ввел слово определитель (Лаплас использовал результат), хотя и не в настоящем значении, а скорее применительно к дискриминанту кванта . Гаусс также пришел к понятию взаимных (обратных) определителей и очень близко подошел к теореме умножения.

Следующим важным участником является Бине (1811, 1812), который формально сформулировал теорему, относящуюся к произведению двух матриц из m столбцов и n строк, что для особого случая m = n сводится к теореме умножения. В тот же день (30 ноября 1812 г.), когда Бине представил свой доклад в Академию, Коши также представил доклад на эту тему. (См. формулу Коши - Бине.) Здесь он использовал слово определитель в его нынешнем смысле, резюмировал и упростил то, что было тогда по этому вопросу, улучшил обозначения и далорема умножения с доказательством более удовлетворительным, чем у Бине. С него начинается теория в целом.

Следующей фигурой был Якоби (с 1827 г.). Он рано использовал функциональный детерминант, который позже Сильвестр назвал якобианом, и в своих мемуарах в Crelle's Journal за 1841 год он специально рассматривает этот предмет, а также класс функций, которые Сильвестр дал альтернативы. Примерно во время последних мемуаров Якоби, Сильвестр (1839) и Кэли начали свою работу.

Изучение особых форм детерминант было естественным результатом завершение общей теории. Осесимметричные детерминанты изучались Лебегом, Гессе и Сильвестром; персимметричные детерминанты Сильвестра и Ханкеля ; циркулянты от каталонца, Споттисвуд, Глэйшер и Скотт; косые детерминанты и пфаффианы в связи с теорией ортогонального преобразования Кэли; континуанты Сильвестра; вронскианцы (так названы Мюиром ) Кристоффелем и Фробениусом ; составные детерминанты Сильвестра, Рейсса и Пике; Якобианы и гессианы Сильвестра; и симметричные гош-определители от Труди. Первым из учебников по этому предмету был Споттисвуд. В Америке Ханус (1886 г.), Велд (1893 г.) и Мьюир / Мецлер (1933 г.) опубликовали трактаты.

Линейная независимость

Как упоминалось выше, определитель матрицы (например, с вещественными или комплексными элементами) равенство нулю тогда и только тогда, когда определенные-столбцы (или вектор -строки) Матрица линейно зависимы. Таким образом, детерминанты можно использовать для характеристик линейно зависимых векторов. Например, для двух линейно независимых векторов v 1, v 2 в R третий вектор v 3 лежит в плоскость , покрытая первыми тремя векторами точно, если определена матрица 3 × 3, состоит из векторов, равен нулю. Та же идея используется в теории дифференциальных уравнений : заданы n функций f 1 (x),..., f n (x) (обяз, что его можно дифференцировать в n - 1 раз), вронскиан определяется как

$W\; (f\; 1,\dots ,\; fn)\; (x)\; =\; |\; f\; 1\; (x)\; f\; 2\; (x)\; \cdots \; fn\; (x)\; f\; 1\; \prime \; (x)\; f\; 2\; \prime \; (x)\; \cdots \; fn\; \prime \; (x)\; ⋮\; ⋮\; \ddots \; ⋮\; f\; 1\; (n\; -\; 1)\; (x)\; f\; 2\; (\; n\; -\; 1)\; (x)\; \cdots \; fn\; (n\; -\; 1)\; (x)\; |.\; \{\backslash \; Displaystyle\; W\; (f\_\; \{1\},\; \backslash \; ldots,\; f\_\; \{n\})\; (x)\; =\; \{\backslash \; begin\; \{vmatrix\}\; f\_\; \{1\}\; (x)\; f\_\; \{2\}\; (x)\; \backslash \; cdots\; f\_\; \{n\; \}\; (x)\; \backslash \backslash \; f\_\; \{1\}\; \text{'}(x)\; f\_\; \{2\}\text{'}\; (x)\; \backslash \; cdots\; f\_\; \{n\}\; \text{'}(x)\; \backslash \backslash \backslash \; vdots\; \backslash \; vdots\; \backslash \; ddots\; \backslash \; vdots\; \backslash \backslash \; f\_\; \{1\}\; ^\; \{(n-1)\}\; (x)\; f\_\; \{2\}\; ^\; \{(n-1)\}\; (x)\; \backslash \; cdots\; f\_\; \{n\}\; ^\; \{(n-1)\}\; (x)\; \backslash \; end\; \{vmatrix\}\}.\}$

Он отличен от нуля (для некоторого x) в заданном интервале тогда и только тогда, когда данные функции и все их производные до порядка n - 1 линейно независимы. Если можно показать, что вронскиан равенство нулюду на интервале, то в случае аналитических функций это означает, что данные функции линейно зависимы. См. вронскиан и линейная независимость.

Ориентация базиса

Детерминант можно рассматривать как присвоение числа каждую следовать из n векторов в R, используя квадратную матрицу, столбцы которой являются заданными деревьями. Например, ортогональная матрица с элементами в R представляет ортонормированный базис в евклидовом пространстве. Определитель такой определяет, согласуется ли ориентация с ориентацией стандартного базиса или противоположна ему. Если определитель равен +1, базис имеет ту же ориентацию. Если он равен −1, то базис имеет противоположную ориентацию.

В более общем смысле, если определитель A положителен, A представляет сохраняющее ориентацию линейное преобразование (если A является ортогональной матрицей 2 × 2 или 3 × 3, это поворот ), а при отрицательном значении A переключает ориентацию основы.

Объем и определитель Якобиана

Как указано выше, абсолютное значение определителя вещественных векторов равно объему параллелепипеда натянутые этим векторами. Как следствие, если f: R→ R- это линейная карта, представленная матрицей A, а S - любое измеримое подмножество из R, то объем функции f ( S) задается формулой | det (A) | умноженный на объем S. В более общем случае, если линейная карта f: R→ Rпредставлена ​​матрицей A m × n, то размерный объем n- f (S) задается следующим образом:

$объем\; \; (f\; (S))\; =\; det\; (ATA)\; \times \; объем\; \; (S).\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{volume\}\; (f\; (S))\; =\; \{\backslash \; sqrt\; \{\backslash \; det\; \backslash \; left\; (A\; ^\; \{\backslash \; textf\; \{T\}\}\; A\; \backslash \; right)\}\}\; \backslash \; times\; \backslash \; operatorname\; \{volume\}\; (S).\; \}$

Посчитав объем тетраэдра, ограниченного четырьмя точками, их можно использовать для определения линий наклона. Объем любого тетраэдра с учетом его вершин a, b, cи d равенство (1/6) · | det (a− b, b− c, c− d) | или любая другая комбинация пар вершин, которая могла бы образовать покрывающее дерево по вершинам.

Для общей дифференцируемой функции многое из вышеперечисленного переносится на рассмотрение матрицы Якоби функции f. Для

$f:\; R\; n\; \to \; R\; n,\; \{\backslash \; displaystyle\; f:\; \backslash \; mathbf\; \{R\}\; ^\; \{n\}\; \backslash \; rightarrow\; \backslash \; mathbf\; \{R\}\; ^\; \{n\},\}$

матрица Якоби - это n × n матрица, элементы которой заданы как

$D\; (f)\; =\; (\partial \; fi\; \partial \; xj)\; 1\; \le \; i,\; j\; \le \; n.\; \{\backslash \; displaystyle\; D\; (f)\; =\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\; f\_\; \{i\}\}\; \{\backslash \; partial\; x\_\; \{j\}\}\}\; \backslash \; right)\; \_\; \{1\; \backslash \; leq\; i,\; j\; \backslash \; leq\; n\}.\}$

Его определитель, определитель Якоби, появляется во многомерной версии интегрирования с помощью замены : для подходящих функций f и открытого подмножества U из R (область определения f), интеграл по f (U) от некоторой другой функции φ: R→ Rимеет вид

$\int \; f\; (U)\; \varphi \; (v)\; dv\; =\; \int \; U\; \varphi \; (f\; (u))\; |\; det\; (D\; \; f)\; (u)\; |\; d\; u.\; \{\backslash \; Displaystyle\; \backslash \; int\; \_\; \{е\; (U)\}\; \backslash \; phi\; (\backslash \; mathbf\; \{v\})\; \backslash ,\; d\; \backslash \; mathbf\; \{v\}\; =\; \backslash \; int\; \_\; \{U\}\; \backslash \; phi\; (f\; (\backslash \; mathbf\; \{u\}))\; \backslash \; left\; |\; \backslash \; det\; (\backslash \; operatorname\; \{D\}\; f)\; (\backslash \; mathbf\; \{u\})\; \backslash \; right\; |\; \backslash ,\; d\; \backslash \; mathbf\; \{u\}.\}$

Якобиан также встречается в теореме об обратной функции.

Вандермонда определитель (альтернант)

Определитель Вандермонда третьего порядка равенства

$|\; 1\; 1\; 1\; x\; 1\; x\; 2\; x\; 3\; x\; 1\; 2\; x\; 2\; 2\; x\; 3\; 2\; |\; =\; (х\; 3\; -\; х\; 2)\; (х\; 3\; -\; х\; 1)\; (х\; 2\; -\; х\; 1).\; \{\backslash \; displaystyle\; \backslash \; left\; |\; \{\backslash \; begin\; \{array\}\; \{ccc\}\; 1\; 1\; 1\; \backslash \backslash \; x\_\; \{1\}\; x\_\; \{2\}\; x\_\; \{3\}\; \backslash \backslash \; x\_\; \{1\}\; ^\; \{2\}\; x\_\; \{2\}\; ^\; \{2\}\; x\_\; \{3\}\; ^\; \{2\}\; \backslash \; end\; \{array\}\}\; \backslash \; right\; |\; =\; (x\_\; \{3\}\; -x\_\; \{2\})\; (x\_\; \{3\}\; -x\_\; \{1\})\; (x\_\; \{2\}\; -x\_\; \{1\}).\; \}$

В общем, определитель Вандермонда n-го порядка равен

, где правая часть представляет собой продолженное произведение всех разностей, которые могут быть образованы из n (n - 1) / 2 пар чисел, взятых из x 1, x 2,..., x n, с порядком различий, взятых в обратном порядке участвующих суффиксов.

Циркулянты

Второй порядок

$|\; х\; 1\; х\; 2\; х\; 2\; х\; 1\; |\; =\; (х\; 1\; +\; х\; 2)\; (х\; 1\; -\; х\; 2).\; \{\backslash \; displaystyle\; \backslash \; left\; |\; \{\backslash \; begin\; \{array\}\; \{cc\}\; x\_\; \{1\}\; x\_\; \{2\}\; \backslash \backslash \; x\_\; \{2\}\; x\_\; \{1\}\; \backslash \; end\; \{array\}\}\; \backslash \; right\; |\; =\; \backslash \; left\; (x\_\; \{1\}\; +\; x\_\; \{2\}\; \backslash \; right)\; \backslash \; left\; (x\_\; \{1\}\; -x\_\; \{2\}\; \backslash \; right).\}$

Третий порядок

$|\; х\; 1\; х\; 2\; х\; 3\; х\; 3\; х\; 1\; х\; 2\; х\; 2\; х\; 3\; х\; 1\; |\; знак\; равно\; (Икс\; 1\; +\; Икс\; 2\; +\; Икс\; 3)\; (Икс\; 1\; +\; \omega \; Икс\; 2\; +\; \omega \; 2\; Икс\; 3)\; (Икс\; 1\; +\; \omega \; 2\; Икс\; 2\; +\; \omega \; Икс\; 3),\; \{\backslash \; Displaystyle\; \backslash \; left\; |\; \{\backslash \; begin\; \{array\}\; \{ccc\}\; x\_\; \{1\}\; x\_\; \{2\}\; x\_\; \{3\}\; \backslash \backslash \; x\_\; \{3\}\; x\_\; \{1\}\; x\_\; \{2\}\; \backslash \backslash \; x\_\; \{2\}\; x\_\; \{3\}\; x\_\; \{1\}\; \backslash \; end\; \{array\}\}\; \backslash \; right\; |\; =\; \backslash \; left\; (x\_\; \{1\}\; +\; x\_\; \{2\}\; +\; x\_\; \{3\}\; \backslash \; right)\; \backslash \; left\; (x\_\; \{1\}\; +\; \backslash \; omega\; x\_\; \{2\}\; +\; \backslash \; omega\; ^\; \{2\}\; x\_\; \{3\}\; \backslash \; right)\; \backslash \; left\; (x\_\; \{1\}\; +\; \backslash \; omega\; ^\; \{2\}\; x\_\; \{2\}\; +\; \backslash \; omega\; x\_\; \{3\}\; \backslash \; right),\}$

где ω и ω - комплексные кубические корни из 1. В общем, Циркулянтный определитель n- го порядка равенство

$|\; x\; 1\; x\; 2\; x\; 3\; \cdots \; x\; n\; x\; n\; x\; 1\; x\; 2\; \cdots \; x\; n\; -\; 1\; x\; n\; -\; 1\; x\; n\; x\; 1\; x\; n\; -\; 2\; ⋮\; ⋮\; ⋮\; x\; 2\; x\; 3\; x\; 4\; \cdots \; x\; 1\; |\; Знак\; равно\; \prod \; J\; знак\; равно\; 1\; N\; (Икс\; 1\; +\; Икс\; 2\; \omega \; J\; +\; Икс\; 3\; \omega \; J\; 2\; +\; \cdots \; +\; Xn\; \omega \; Jn\; -\; 1),\; \{\backslash \; Displaystyle\; \backslash \; left\; |\; \{\backslash \; begin\; \{array\}\; \{ccccc\}\; x\_\; \{1\}\; x\_\; \{2\}\; x\_\; \{3\}\; \backslash \; cdots\; x\_\; \{n\}\; \backslash \backslash \; x\_\; \{n\}\; x\_\; \{1\}\; x\_\; \{2\}\; \backslash \; cdots\; x\_\; \{n-1\}\; \backslash \backslash \; x\_\; \{n-1\}\; x\_\; \{n\}\; x\_\; \{1\}\; \backslash \; cdots\; x\_\; \{n-2\}\; \backslash \backslash \backslash \; vdots\; \backslash \; vdots\; \backslash \; vdots\; \backslash \; ddots\; \backslash \; vdots\; \backslash \backslash \; x\_\; \{2\}\; x\_\; \{3\}\; x\_\; \{4\}\; \backslash \; cdots\; x\_\; \{1\}\; \backslash \; конец\; \{массив\}\}\; \backslash \; right\; |\; =\; \backslash \; prod\; \_\; \{j\; =\; 1\}\; ^\; \{n\}\; \backslash \; left\; (x\_\; \{1\}\; +\; x\_\; \{2\}\; \backslash \; omega\; \_\; \{j\}\; +\; x\_\; \{3\}\; \backslash \; omega\; \_\; \{j\}\; ^\; \{2\}\; +\; \backslash \; cdots\; +\; x\_\; \{n\}\; \backslash \; omega\; \_\; \{j\}\; ^\; \{n-1\}\; \backslash \; right),\}$

где ω j - корень n-й степени из 1.

• Портал математики

• Определитель Коши
• Определитель Кэли - Менгера
• Определитель Дьедонне
• Имманант
• Постоянный
• Определитель Слейтера

• Axler, Sheldon Jay (1997), Linear Algebra Done Done Done Done Right (2-е изд.), Springer-Verlag, ISBN 0-387-98259-0
• де Бур, Карл (1990), «Пустое упражнение» (PDF), Информационный бюллетень ACM SIGNUM, 25 (2): 3–7, doi : 10.1145 / 122272.122273, S2CID 62780452.
• Lay, David C. (22 августа, 2005), Линейная алгебра и ее приложения (3-е изд.), Эддисон Уэсли, ISBN 978-0-321-28713-7
• Мейер, Карл Д. (15 2001 г.), Матричный анализ и прикладная линейная алгебра, Общество промышленной и прикладной математики (SIAM), ISBN 978-0-89871-454-8, заархивировано из оригинал 31.10.2009
• Мюр, Томас (1960) [1933], Трактат по теории детерминант, переработанный и дополненный Уильямом Х. Метцлером, Нью-Йорк, Нью-Йорк: Dover
• Пул, Дэвид (2006), Linear Algebra: A Modern Introduction (2 ed.), Brooks / Cole, ISBN 0-534 -99845-3
• Г. Бейли Прайс (1947) «Некоторые тождества в теории детерминантов», American Mathematical Monthly 54: 75–90 MR 0019078
• Хорн, Р. А.; Джонсон, CR (2013), Матричный анализ (2-е изд.), Cambridge University Press, ISBN 978-0-521-54823-6
• Антон, Ховард (2005), Элемент линейный Алгебра (прикладная версия) (9-е изд.), Wiley International
• Леон, Стивен Дж. (2006), Линейная алгебра с приложениями (7-е изд.), Пирсон Прентис Холл

The Wikibook У линейной алгебры есть страница по теме: Определители

Викисточник содержит текст Британской энциклопедии 1911 года статьи Определитель.

• Супруненко Д.А. (2001) [1994], Энциклопедия математики, EMS Press
• Вайсштейн, Эрик У. «Определитель». MathWorld.
• О'Коннор, Джон Дж. ; Робертсон, Эдмунд Ф., «Матрицы и детерминанты», Архив истории математики MacTutor, Университет Сент-Эндрюс.
• Интерактивная программа детерминантов и Учебное пособие
• Линейная алгебра: детерминанты. Вычисляйте детерминанты матриц до 6-го порядка, используя расширение Лапласа по вашему выбору.
• Матрицы и линейная алгебра на страницах самых ранних ранних применений
• Детерминанты объясняются простым в 4-м Глава как часть курса линейной алгебры.
• Обучающее видео по взятию определителя матрицы размера nxn (Академия Хана)
• "Определитель". Суть линейной алгебры - через YouTube.