Волновая функция

Математическое описание квантового состояния системы; комплекснозначная амплитуда вероятности, вероятности результатов измерений, выполненных в системе, могут быть получены из нее Сравнение классической и концепции квантового гармонического осциллятора для одного бесспиновая частица. Эти два процесса сильно различаются. Классический процесс (A - B) представлен как движение частиц по траектории. У квантового процесса (C - H) такой траектории нет. Скорее он представлен в виде волны; здесь вертикальная ось показывает действующую часть (синий цвет) и мнимую часть (красный цвет) волновой функции. На панелях (C - F) показаны четыре различных решения для стоячей волны уравнения Шредингера. На панелях (G - H) показаны две разные волновые функции, которые являются решениями уравнения Шредингера, но не стоячими волнами.

A волновая функция в квантовой физике является математическим описанием квантовое состояние изолированной квантовой системы. Волновая функция представляет собой комплексную амплитуду вероятности, и вероятности результатов измерений, выполненных в системе, могут быть получены из нее. Наиболее распространенные символы для волновой функции - это греческие буквы ψ и Ψ (нижний регистр и заглавная буква psi соответственно).

Волновая функция - это функция от степеней свободы, соответствующему некоторому максимальному набору коммутирующих наблюдаемых. Как только такое представление выбрано, волновая функция может быть получена из квантового состояния.

Данная система выбора коммутирующих степеней свободы для использования не является уникальным, и, соответственно, область волновой функцией также не является уникальной. Например, это может быть функция всех частиц космических пространств или сигналов всех космических сигналов ; они связаны с помощью преобразования Фурье. Некоторые частицы, такие как электроны и фотоны, ненулевой спин, и волновая функция таких частиц включает спин как внутреннюю дискретную степень свободы; могут быть включительно дискретные переменные, такие как изоспин. Когда система имеет внутренние степени свободы, волновая функция в каждой точке непрерывных степеней свободы (например, в каждой области степеней) присваивает комплексное число для каждого возможного значения дискретных степеней свободы (например, z-компонентное вращение) - эти значения часто в матрице-столбце (например, вектор-столбец 2 × 1 для нерелятивистского электрона со спином ⁄ 2).

Согласно принципу суперпозиции квантовой механики, волновые функции можно складывать и умножать на комплексные числа, чтобы сформировать новые волновые функции и сформировать гильбертово пространство. Внутренний продукт между двумя волновыми функциями является мерой перекрытия между физическими состояниями и используется в основеополагающей вероятностной интерпретации квантовой механики, правиле Борна, связывающим вероятности перехода со внутренними продуктами. Уравнение Шредингера определяет, как волновые функции развиваются во времени, волновая функция качественно ведет себя так же, как и другие волны волны, такие как волны на воде или волны на струне, потому что уравнение Шредингера математически разновидностью волнового уравнения. Это объясняет название «волновая функция» и порождает дуальность волны-частица. Волновая функция в квантовой механике представляет своего рода физическое явление, все еще открытое для различных интерпретаций, которое фундаментально отличается от такового для классических механических волнений.

В Борн в статистической интерпретации нерелятивистской квантовой механики, квадрат модуля волновой функции | ψ | Действующее , интерпретируемое как плотность из измерения частиц как находящейся в заданном месте представляет собой имеющее заданный импульс в заданное время и, возможно, имеющее значение для дискретных степеней свободы. Интеграл этой величины по всем степеням свободы системы должен быть равен 1 в соответствии с вероятностной интерпретацией. Это общее требование, соответствующее удовлетворять волновая функция, называется условием нормировки. Можно измерить только ее относительную фазу и относительное значение - ее значение по отдельной фазе ничего не говорит о измеримых наблюдаемых; необходимо применить квантовые операторы, собственные значения которые соответствуют наборам результатов измерений, к волновой функции ψ и вычислить распределение для измеримых величин.

Содержание

• 1 Историческая справка
  • 1.1 Волновые функции и волновые уравнения в современных теориях
• 2 Определение бесспиновая частица в одном измерении
  • 2.1 Волновые функции пространственного положения
    • 2.1.1 Условие нормализации
    • 2.1.2 Квантовые состояния как поверхность
  • 2.2 Волновые функции в пространстве импульса
  • 2.3 Связь между позиционным и импульсным представлениями
• 3 Определения (другие случаи)
  • 3.1 Одночастичные состояния в трехмерном пространстве
  • 3.2 Многочастичные состояния в трехмерном позиционном пространстве
    • 3.2.1 Вероятностная интерпретация
• 4 Временная зависимость
• 5 Нерелятивистские примеры
  • 5.1 Конечный потенциальный барьер
  • 5.2 Квантовый гармонический осциллятор
  • 5.3 Атом двигатель
• 6 Волновые функции и функциональные пространства
  • 6.1 Структура пространства
  • 6.2 Представления пространства
  • 6.3 Внутренний продукт
  • 6.4 Гильбертово пространство
  • 6.5 Общие гильберто в ы пространства
  • 6.6 Упрощенное описание
• 7 Подробнее о волновых функциях и абстрактном пространстве состояний
• 8 Онтология
• 9 См. Также
• 10 Примечания
• 11 Ссылки
• 12 Источники
• 13 литература
• 14ние ссылки

Историческая справка

В 1905 году Альберт Эйнштейн постулировал объемость между видом $f\; \{\backslash \; displaystyle\; f\}$фотона и его энергии $E\; \{\backslash \; displaystyle\; E\}$, $E\; =\; hf\; \{\backslash \; displaystyle\; E\; =\; hf\}$, а в 1916 году соответствующее отношение между импульсом $p\; \{\backslash \; displaystyle\; p\}$и длиной волны $\lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\}$, $\lambda \; =\; hp\; \{\backslash \; displaystyle\; \backslash \; lambda\; =\; \{\backslash \; dfrac\; \{h\}\; \{p\}\}\}$, где $h\; \{\backslash \; displaystyle\; h\}$- постоянная Планка. В 1923 году Де Бройль был первым, кто предположил, что отношение $\lambda \; =\; hp\; \{\backslash \; displaystyle\; \backslash \; lambda\; =\; \{\backslash \; frac\; \{h\}\; \{p\}\}\}$, теперь называемое Соотношение Бройля справедливо для массивных частиц, главным ключом к разгадке которого является лоренц-инвариантность, и это можно рассматривать как отправную точку для современного развития квантовой механики. Уравнения отличается дуальность волны-частица как для безмассовых, так и для массивных частиц.

В 1920-х и 1930-х годах квантовая механика развивалась с использованием исчисления и линейной алгебры. Технику исчисления использовали Луи де Бройль, Эрвин Шредингер и другие, разработавшие «волновую механику ». Среди тех, кто применял методы линейной алгебры, были Вернер Гейзенберг, Макс Борн и другие, разработавшие «матричную механику». Впечатление Шредингер показал, что эти два подхода эквивалентны.

В 1926 году Шредингер опубликовал знаменитое волновое уравнение, теперь названное его именем, уравнение Шредингера. Это уравнение было основано на классическом сохранении энергии с использованием квантовых операторов и используемых де Бройля, а решения для функций для квантовой. Однако никто не понимает, как это интерпретировать. Сначала Шредингер и другие думали, что волновая функция собой представляет собой частицы, которые разбросаны, причем большая часть частиц находится там, где волновая функция велика. Было показано, что это несовместимо с упругим рассеяние волнового пакета на мишени; он распространяется во всех направлениях. Хотя рассеянная частица может разлететься в любом направлении, она не разбивается и не уносится во всех направлениях. В 1926 году Борн представил перспективу амплитуды вероятности. Это напрямую связывает расчеты квантовой механики с вероятными экспериментальными наблюдениями. Это принято как часть копенгагенской интерпретации квантовой механики. Есть много других интерпретаций квантовой механики. В 1927 году Хартри и Фок сделали первый шаг в попытке решить волновую функцию N-тела и разработали цикл самосогласования: итеративный алгоритм для аппроксимации решения. Теперь он также известен как метод Хартри - Фока. Определитель Слейтера и постоянный (из матрицы ) был определенным методом, предложенного Джоном С. Слейтером.

Шредингер действительно столкнулся с уравнением для волновой функции, которое удовлетворяло релятивистскому закон сохранения энергии до того, как он опубликовал нерелятивистское уравнение, но отбросило его, поскольку оно предсказывало отрицательные вероятности и отрицательные энергии. В 1927 году Клейн, Гордон и Фок также нашли его, но учли электромагнитное взаимодействие и доказали, что это Лоренц. инвариант. Де Бройль также пришел к тому же уравнению в 1928 году. Это релятивистское волновое уравнение наиболее широко как уравнение Клейна - Гордона.

. В 1927 году Паули феноменологически нашел нерелятивистское уравнение описывают частицы со спином 1/2 в электромагнитных полях, теперь называемые уравнением Паули. Паули обнаружил, что волновая функция не описывалась одной сложной функции пространства и времени, а требовалось два комплексных числа, которые соответствуют состояниям фермиона со спином +1/2 и -1/2. Вскоре после того, как в 1928 году Дирак нашел уравнение из первого совокупного объединения специальной теории относительности и квантовой механики, примененной к электрону, теперь называемому Дираком. уравнение. В этом случае волновая функция является спинором, представленным четырьмя комплексными компонентами: двумя для электрона и двумя для античастицы электрона, позитрона. В нерелятивистском пределе волновая функция Дирака волновую функцию Паули для электрона. Позже были найдены другие релятивистские волновые уравнения.

Волновые функции и волновые уравнения в современных теориях

Все эти волновые уравнения имеют непреходящее значение. Уравнение Шредингера и уравнение Паули во многих случаях превосходны приближения релятивистских вариантов. Их значительно проще решить практических задач, чем релятивистские аналоги.

Уравнение Клейна - Гордона и уравнение Дирака, хотя и являются релятивистскими, не обеспечат полного примирения квантовой механики и специальной теории относительности. Раздел квантовой механики, в котором эти уравнения изучаются так же, как уравнение Шредингера, часто называемый релятивистской квантовой механикой, хотя и очень успешен, имеет свои ограничения (см., Например, сдвиг Лэмба ) и концептуальные проблемы (см., например, море Дирака ).

Относительность делает неизбежным, что количество частиц в системе непостоянно. Для полного согласования необходима квантовая теория поля. В этой теории волновые уравнения и волновые функции имеют свое место, но в несколько ином обличье. Основными объектами интереса являются не волновые функции, а скорее операторы, так называемые операторы поля (или просто поля, в которых понимается «оператор») на гильбертовом поле состояний (будет описанное в следующем разделе). Оказывается, исходные релятивистские волновые уравнения и их решения по-прежнему необходимы для построения гильбертова пространства. Более, операторы свободных полей, которые (формально) удовлетворяют уравнению, что и поля (формально) удовлетворяют уравнению, что и поля (формально) удовлетворяют уравнению, что и поля (формально).

Таким образом, уравнение Клейна - Гордона (спин 0) и уравнение Дирака (спин ⁄ 2) в этом виде остается в теории. Аналоги более высокого спина включают уравнение Прока (спин 1), уравнение Рариты - Швингера (спин ⁄ 2) и, в более общем плане, Уравнения Баргмана - Вигнера. Для безмассовых свободных полей двумя примерами свободное поле уравнение Максвелла (спин 1) и свободное поле уравнение Эйнштейна (спин 2) для операторов поля. Все они по сути следствия требований лоренц-инвариантности. Их решения преобразовывать при преобразовании Лоренца заданным образом, то есть при определенном представлении группы Лоренца, а также при некоторых других разумных требованиях, например принцип кластерной декомпозиции с последствиями для причинной связи достаточно, чтобы исправить уравнения.

Это применимо к уравнениям свободного поля; играть не включено. Если плотность лагранжиана включает (взаимодействие), то формализм лагранжиана уравнение движения на классическом уровне. Это уравнение может быть очень сложным и не поддающимся решением. Любое решение будет относиться к фиксированному количеству частиц и не будет учитывать «взаимодействие», включает в себя создание и уничтожение частиц, а не внешние потенциалы, как в обычной «квантовой» квантовой теории.

В теории струн ситуация остается аналогичной. Например, волновая функция в импульсном пространстве играет роль разложения Фурье в общем состоянии частиц (струны) с импульсом, который четко не определен.

Определение (одна бесспиновая частица в одном измерении)

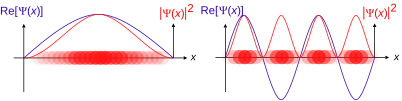Стоячие волны для частиц в ящике, примеры стационарных состояний. 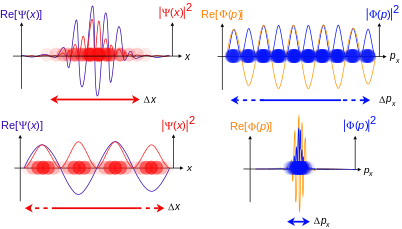волны движущихся частиц частиц. действительные части волновая функция положения Ψ (x) и волновая функция импульса Φ (p), а также соответствующие плотности вероятности | Ψ (x) | и | Φ (p) | для одной частицы со спином 0 в одном измерении x или p. Цветовая непрозрачность частиц плотности вероятности (не волновой) частицы в позиции x функции или импульсе p.

А пока рассмотрим простой случай нерелятивистской одиночной частицы без вращения в одном пространственном измерении. Более общие случаи обсуждаются ниже.

Волновые функции пространственного положения

Состояние таких частиц полностью описывается ее волновой функцией

$\Psi \; (x,\; t),\; \{\backslash \; displaystyle\; \backslash \; Psi\; (x,\; t)\; \backslash ,,\}$

где x - позиция, а t - время. Это комплекс действующая функция двух различных чисел x и t.

Для одной бесспиновой частицы в 1d, если волновая функция интерпретируется как амплитуда вероятности, квадрат модуля волновой функции, положительное действующее число

$|\; \Psi \; (x,\; t)\; |\; 2\; знак\; равно\; \Psi \; *\; (Икс,\; Т)\; \Psi \; (Икс,\; Т)\; =\; \rho \; (Икс,\; Т),\; \{\backslash \; Displaystyle\; \backslash \; влево\; |\; \backslash \; Пси\; (х,\; т)\; \backslash \; вправо\; |\; ^\; \{2\}\; =\; \backslash \; Пси\; ^\; \{*\}\; (x,\; t)\; \backslash \; Psi\; (x,\; t)\; =\; \backslash \; rho\; (x,\; t),\}$

интерпретируется как плотность вероятности того, что частица находится в точке x. Звездочка указывает на комплексный конъюгат . Если положение частиц измерено, ее местоположение не может быть определено с помощью волновой функции, но описывается с помощью распределения вероятностей.

Условие измерения распределения

Вероятность того, что ее положение x будет в a ≤ x ≤ b, является интегралом плотности по этому интервалу:

$P\; a\; \le \; x\; \le \; b\; (t)\; =\; \int \; ab\; |\; \Psi \; (x,\; t)\; |\; 2\; dx\; \{\backslash \; displaystyle\; P\_\; \{a\; \backslash \; leq\; x\; \backslash \; leq\; b\}\; (t)\; =\; \backslash \; int\; \backslash \; limits\; \_\; \{a\}\; ^\; \{b\}\; \backslash ,\; |\; \backslash \; Psi\; (x,\; t)\; |\; ^\; \{2\}\; dx\}$

где t - время измерения частиц. Это приводит к условию нормировки :

$\int \; -\; \infty \; \infty \; |\; \Psi \; (x,\; t)\; |\; 2\; dx\; =\; 1,\; \{\backslash \; displaystyle\; \backslash ,\; \backslash \; int\; \backslash \; limits\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; \backslash ,\; |\; \backslash \; Psi\; (x,\; t)\; |\; ^\; \{2\}\; dx\; =\; 1\; \backslash ,,\}$

потому что если частицу измерить, есть 100% вероятность, что она где-то будет.

Данная система использует различные волновые функции (в любой момент времени) образует абстрактное математическое пространство, что означает, что можно складывать вместе различные волновые функции, и умножать волновые функции на комплексные числа (подробности см)). в векторном изображении ). Технически из-за стабилизации волновых функций образуют проективное пространство , а не обычное векторное пространство. Это векторное пространство бесконечно- мерно, потому что не существует конечного набора функций, которые можно складывать вместе в различных комбинациях для создания каждой возможной функции. Кроме того, это гильбертово пространство, потому что что что внутреннее произведение двух волновых функций Ψ 1 и Ψ 2 можно определить как комплексное число (в момент времени t)

$(\Psi \; 1,\; \Psi \; 2)\; =\; \int \; -\; \infty \; \infty \; \Psi \; 1\; \ast \; (x,\; t)\; \Psi \; 2\; (x,\; t)\; dx.\; \{\backslash \; Displaystyle\; (\backslash \; Psi\; \_\; \{1\},\; \backslash \; Psi\; \_\; \{2\})\; =\; \backslash \; int\; \backslash \; limits\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; \backslash ,\; \backslash \; Psi\; \_\; \{1\}\; ^\; \{*\}\; (x,\; т)\; \backslash \; Psi\; \_\; \{2\}\; (x,\; t)\; dx.\}$

Более подробная информация представлена ​​ниже. Хотя внутреннее произведение двух волновых функций является комплексным, внутреннее произведение волновой функции Ψ на себя,

$(\Psi ,\; \Psi )\; =\; \Vert \; \Psi \; \Vert \; 2,\; \{\backslash \; displaystyle\; (\backslash \; Psi,\; \backslash \; Psi)\; =\; \backslash \; |\; \backslash \; Psi\; \backslash \; |\; ^\; \{2\}\; \backslash ,,\}$

всегда является положительным вещественным числом. Число || Ψ || (не || Ψ ||) называется нормой волновой функции Ψ.

Если (Ψ, Ψ) = 1, то Ψ нормализовано. Если Ψ не нормализовано, то деление на его норму дает нормированную функцию Ψ / || Ψ ||. Две волновые функции Ψ 1 и Ψ 2 являются ортогональными, если (Ψ 1, Ψ 2) = 0.Если они нормализованы и ортогональны, они ортонормированы. Ортогональность (а значит, и ортонормированность) волновых функций не является условием, но поучительно для рассмотрения, поскольку это линейная независимость функций. В линейной комбинации ортогональных волновых функций Ψ n мы имеем,

$\Psi \; =\; \sum \; nan\; \Psi \; n,\; an\; =\; (\Psi \; n,\; \Psi )\; (\Psi \; n,\; \Psi \; n)\; \{\backslash \; displaystyle\; \backslash \; Psi\; =\; \backslash \; sum\; \_\; \{n\}\; a\_\; \{n\}\; \backslash \; Psi\; \_\; \{n\}\; \backslash ,,\; \backslash \; quad\; a\_\; \{n\}\; =\; \{\backslash \; frac\; \{(\backslash \; Psi\; \_\; \{n\},\; \backslash \; Psi)\}\; \{(\backslash \; Psi\; \_\; \{n\},\; \backslash \; Psi\; \_\; \{n\})\}\}\}$

Если бы волновые функции Ψ n были неортогональными, то коэффициенты было бы проще получить.

Квантовые состояния как электрические

В копенгагенской интерпретации квадрат модуля внутреннего произведения (комплексное число) дает действительное число

$|\; (\Psi \; 1,\; \Psi \; 2)\; |\; 2\; знака\; равно\; п\; (\Psi \; 2\; \to \; \Psi \; 1),\; \{\backslash \; Displaystyle\; \backslash \; влево\; |\; (\backslash \; Psi\; \_\; \{1\},\; \backslash \; Psi\; \_\; \{2\})\; \backslash \; right\; |\; ^\; \{2\}\; =\; P\; \backslash \; left\; (\backslash \; Psi\; \_\; \{2\}\; \backslash \; rightarrow\; \backslash \; Psi\; \_\; \{1\}\; \backslash \; right)\; \backslash ,,\}$

что, если предположить, что обе волновые функции нормализованы, интерпретируется как вероятность того, что волновая функция Ψ 2«схлопнется» на новом волну функция Ψ 1 при измерении наблюдаемых, собственных значений результаты измерений, причем Ψ 1 является собственным вектором результирующего собственного значения. Это правило Борна и один из фундаментальных постулатов квантовой механики.

В данном моменте времени все значения волновой функции Ψ (x, t) являются компонентами вектора. Их бесчисленно бесконечно много, и вместо суммирования используемое интегрирование. В брэкет-нотации этот вектор записывается как

$|\; \Psi \; (t)⟩\; =\; \int \; \Psi \; (x,\; t)\; |\; х⟩\; dx\; \{\backslash \; displaystyle\; |\; \backslash \; Psi\; (t)\; \backslash \; rangle\; =\; \backslash \; int\; \backslash \; Psi\; (x,\; t)\; |\; x\; \backslash \; rangle\; dx\}$

и называется «вектор квантового состояния» или просто «квантовое состояние». У понимания волновых функций как представления элементов абстрактного пространства есть несколько преимуществ:

• Все мощные инструменты линейной алгебры :
  • Линейная алгебра объясняет, как векторному пространству может быть дан базис, любой вектор в векторном рекламе может быть выражен в этом базисе.
  • Нотация Бра-кет может интендант для управления системными функциями.
• Идея факт, что квантовой теории поля абстрактного пространства, полностью общего для состояния квантовой механики и квантовой теории поля. Я о том, что квантовые состояния комплексными «волновыми» функциями верно только в определенных условиях.

Параметр времени часто подавляется, и будет следующим. Координата x - это непрерывный индекс. | X⟩ - это базисные электрические, которые являются ортонормированными, поэтому их внутренний продукт является дельта-функцией ;

$⟨x\; \prime \; |\; знак\; x⟩\; равно\; \delta \; (x\; \prime \; -\; x)\; \{\backslash \; displaystyle\; \backslash \; langle\; x\; \text{'}|\; x\; \backslash \; rangle\; =\; \backslash \; delta\; (x\text{'}-x)\}$

таким образом

$⟨x\; \prime \; |\; \Psi ⟩\; =\; \int \; \Psi \; (x)\; ⟨x\; \prime \; |\; Икс⟩\; dx\; знак\; равно\; \Psi \; (Икс\; \text{'})\; \{\backslash \; Displaystyle\; \backslash \; langle\; x\text{'}\; |\; \backslash \; Psi\; \backslash \; rangle\; =\; \backslash \; int\; \backslash \; Psi\; (x)\; \backslash \; langle\; x\; \text{'}|\; x\; \backslash \; rangle\; dx\; =\; \backslash \; Psi\; (x\; \text{'})\}$

и

$|\; \Psi ⟩\; =\; \int \; |\; x⟩\; ⟨x\; |\; \Psi ⟩\; d\; x\; =\; (\int \; |\; x⟩\; ⟨x\; |\; d\; x)\; |\; \Psi ⟩\; \{\backslash \; Displaystyle\; |\; \backslash \; Psi\; \backslash \; rangle\; =\; \backslash \; int\; |\; x\; \backslash \; rangle\; \backslash \; langle\; x\; |\; \backslash \; Psi\; \backslash \; rangle\; dx\; =\; \backslash \; left\; (\backslash \; int\; |\; x\; \backslash \; rangle\; \backslash \; langle\; x\; |\; dx\; \backslash \; right)\; |\; \backslash \; Psi\; \backslash \; rangle\}$

, который освещает оператор идентичности

$I\; =\; \int \; |\; x⟩\; ⟨x\; |\; d\; x.\; \{\backslash \; Displaystyle\; I\; =\; \backslash \; int\; |\; x\; \backslash \; rangle\; \backslash \; langle\; x\; |\; dx\; \backslash ,.\}$

Нахождение оператора тождества в базисе позволяет явно выразить абстрактное состояние в базисе и т. д. (внутренний продукт между двумя базисными состояниями).

Волновые функции импульсного пространства

Частица также имеет волновую функцию в импульсном пространстве :

$\Phi \; (p,\; t)\; \{\backslash \; displaystyle\; \backslash \; Phi\; (p,\; t)\}$

где p - импульс в одном измерении, которое может быть величиной от −∞ до + ∞, а t - время.

Аналогично случаю положения, внутреннее произведение двух волновых функций Φ 1 (p, t) и Φ 2 (p, t) может быть определено как:

$(\Phi \; 1,\; \Phi \; 2)\; =\; \int \; -\; \infty \; \infty \; \Phi \; 1\; \ast \; (p,\; t)\; \Phi \; 2\; (p,\; t)\; dp.\; \{\backslash \; displaystyle\; (\backslash \; Phi\; \_\; \{1\},\; \backslash \; Phi\; \_\; \{2\})\; =\; \backslash \; int\; \backslash \; limits\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; \backslash ,\; \backslash \; Phi\; \_\; \{1\}\; ^\; \{*\}\; (p,\; t)\; \backslash \; Phi\; \_\; \{2\}\; (p,\; t)\; dp\; \backslash ,.\}$

Одно из конкретных решений не зависящего от времени уравнения Шредингера:

$\Psi \; p\; (x)\; =\; eipx\; /\; \hslash ,\; \{\backslash \; displaystyle\; \backslash \; Psi\; \_\; \{p\}\; (x)\; =\; e\; ^\; \{ipx\; /\; \backslash \; hbar\},\}$

a плоская волна, которую можно использовать при описании частиц с импульсами в точности p, поскольку она является собственной функцией параметра импульса. Эти функции нельзя нормализовать до единицы (они не интегрируются с квадратом), поэтому на самом деле они не являются элементами физического гильбертова пространства. Множество

$\{\Psi \; p\; (x,\; t),\; -\; \infty \; \le \; p\; \le \; \infty \}\; \{\backslash \; displaystyle\; \backslash \; \{\backslash \; Psi\; \_\; \{p\}\; (x,\; t),\; -\; \backslash \; infty\; \backslash \; leq\; p\; \backslash \; leq\; \backslash \; infty\; \backslash \}\}$

формирует так называемый импульсный базис . Этот «базис» не является базисом в обычном математическом смысле. Во-первых, поскольку функции не нормализуются, они вместо этого нормализуются до дельта-функций,

$(\Psi \; p,\; \Psi \; p\; \prime )\; =\; \delta \; (p\; -\; p\; \prime ).\; \{\backslash \; displaystyle\; (\backslash \; Psi\; \_\; \{p\},\; \backslash \; Psi\; \_\; \{p\; \text{'}\})\; =\; \backslash \; delta\; (p-p\text{'}).\}$

Во-вторых, хотя они линейно независимы, их слишком много (они образуют несчетное множество) для основы физического гильбертова пространства. Их все еще можно использовать для выражения всех функций в нем с помощью преобразований Фурье, как описано ниже.

Отношения между представлениями положения и импульса

Представления x и p:

$|\; \Psi ⟩\; =\; I\; |\; \Psi ⟩\; =\; \int \; |\; x⟩\; ⟨x\; |\; \Psi ⟩\; d\; x\; =\; \int \; \Psi \; (x)\; |\; х⟩\; д\; х,\; |\; \Psi ⟩\; =\; I\; |\; \Psi ⟩\; =\; \int \; |\; p⟩\; ⟨p\; |\; D\; p\; =\; \int \; \Phi \; (p)\; |\; п⟩\; д\; п.\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; |\; \backslash \; Psi\; \backslash \; rangle\; =\; I\; |\; \backslash \; Psi\; \backslash \; rangle\; =\; \backslash \; int\; |\; x\; \backslash \; rangle\; \backslash \; langle\; x\; |\; \backslash \; Psi\; \backslash \; rangle\; dx\; =\; \backslash \; int\; \backslash \; Psi\; (x)\; |\; x\; \backslash \; rangle\; dx,\; \backslash \backslash \; |\; \backslash \; Psi\; \backslash \; rangle\; =\; I\; |\; \backslash \; Psi\; \backslash \; rangle\; =\; \backslash \; int\; |\; p\; \backslash \; rangle\; \backslash \; langle\; p\; |\; \backslash \; Psi\; \backslash \; rangle\; dp\; =\; \backslash \; int\; \backslash \; Phi\; (p)\; |\; п\; \backslash \; рангл\; дп.\; \backslash \; end\; \{выровнено\}\}\}$

Теперь возьмем проекцию состояния на собственные функции количества движения, используя последнее выражение в двух уравнениях,

$\int \; \Psi \; (x)\; ⟨p\; |\; x⟩\; d\; x\; =\; \int \; \Phi \; (p\; \prime )\; ⟨p\; |\; p\; \prime ⟩\; d\; p\; \prime \; =\; \int \; \Phi \; (p\; \prime )\; \delta \; (p\; -\; p\; \prime )\; d\; p\; \prime \; =\; \Phi \; (p).\; \{\backslash \; Displaystyle\; \backslash \; int\; \backslash \; Psi\; (x)\; \backslash \; langle\; p\; |\; x\; \backslash \; rangle\; dx\; =\; \backslash \; int\; \backslash \; Phi\; (p\; \text{'})\; \backslash \; langle\; p\; |\; p\; \text{'}\backslash \; rangle\; dp\text{'}\; =\; \backslash \; int\; \backslash \; Phi\; (p\; \text{'})\; \backslash \; delta\; (p\; -p\text{'})\; dp\; \text{'}=\; \backslash \; Phi\; (p).\}$

Затем, используя известное выражение для подходящего образом нормированных состояний количества движения в решениях позиционного представления свободного уравнения Шредингера

$⟨x\; |\; p⟩\; =\; p\; (x)\; =\; 1\; 2\; \pi \; \hslash \; e\; i\; \hslash \; p\; x\; \Rightarrow \; ⟨p\; |\; Икс⟩\; знак\; равно\; 1\; 2\; \pi \; \hslash \; е\; -\; я\; \hslash \; px,\; \{\backslash \; displaystyle\; \backslash \; langle\; x\; |\; p\; \backslash \; rangle\; =\; p\; (x)\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{2\; \backslash \; pi\; \backslash \; hbar\}\}\}\; e\; ^\; \{\{\backslash \; frac\; \{i\}\; \{\backslash \; hbar\}\}\; px\}\; \backslash \; Rightarrow\; \backslash \; langle\; p\; |\; x\; \backslash \; rangle\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{2\; \backslash \; pi\; \backslash \; hbar\}\}\}\; e\; ^\; \{-\; \{\backslash \; frac\; \{i\}\; \{\backslash \; hbar\}\}\; px\},\}$

получаем

$\Phi \; (\; p)\; =\; 1\; 2\; \pi \; \hslash \; \int \; \Psi \; (x)\; e\; -\; i\; \hslash \; pxdx.\; \{\backslash \; displaystyle\; \backslash \; Phi\; (p)\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{2\; \backslash \; pi\; \backslash \; hbar\}\}\}\; \backslash \; int\; \backslash \; Psi\; (x)\; e\; ^\; \{-\; \{\backslash \; frac\; \{i\}\; \{\backslash \; hbar\}\}\; пикселей\; \}\; dx\; \backslash ,.\}$

Аналогично, используя собственные функции положения,

$\Psi \; (x)\; =\; 1\; 2\; \pi \; \hslash \; \int \; \Phi \; (p)\; ei\; \hslash \; pxdp.\; \{\backslash \; displaystyle\; \backslash \; Psi\; (x)\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{2\; \backslash \; pi\; \backslash \; hbar\}\}\}\; \backslash \; int\; \backslash \; Phi\; (p)\; e\; ^\; \{\{\backslash \; frac\; \{i\}\; \{\backslash \; hbar\}\}\; px\}\; dp\; \backslash ,.\}$

Таким образом, обнаружено, что волновые пространственного положения и пространственные изображения являются преобразованиями Фурье друг друга. Две волновые функции содержат одинаковую информацию, и любую одну достаточно для любого вычисления свойства частицы. Как представлены элементы абстрактного физического гильбертова пространства, элементы которых являются возможными состояниями рассматриваемой системы, они представляют один и тот же вектор состояния, следовательно, идентичные физические состояния, но в целом они не равны, если рассматривать их как интегрируемые с квадратом функции.

Практическая функция пространственного положения используется гораздо чаще, чем волновая функция импульсного пространства. Потенциал, входящий в уравнение (Шредингера, Дирака и т. Д.), Определяет, на каком основании описание будет проще всего. Для гармонического осциллятора x и p входят симметрично, поэтому не имеет значения, какое описание использовать. То же уравнение (по модулю констант) получается. Из этого следует, с некоторой запоздалой мыслью, факт: решения волнового уравнения волнового осциллятора являются собственными функциями преобразования Фурье в L.

Определения (другие случаи)

Ниже приведены общие формы волновой функции для систем более высоких и измерений с большим количеством частиц, а также включающие другие степени свободы, кроме координат или компонентов импульса.

Одночастичное состояние в трехмерном пространстве пространственного измерения

Волновая функция позиционно-пространственной волновой функции отдельных частиц без спина в трех пространственных измерениях на одном пространственном измерении выше:

$\Psi \; (r,\; t)\; \{\; \backslash \; displaystyle\; \backslash \; Psi\; (\backslash \; mathbf\; \{r\},\; t)\}$

, где r - векторное положение в трехмерном пространстве, а t время. Как всегда, Ψ (r, t) является комплексной функцией вещественного числа. Как один вектор в нотации Дирака

$|\; \Psi \; (t)⟩\; =\; \int \; d\; 3\; r\; \Psi \; (r,\; t)\; |\; р⟩\; \{\backslash \; Displaystyle\; |\; \backslash \; Psi\; (t)\; \backslash \; rangle\; =\; \backslash \; int\; d\; ^\; \{3\}\; \backslash !\; \backslash \; mathbf\; \{r\}\; \backslash ,\; \backslash \; Psi\; (\backslash \; mathbf\; \{r\},\; t)\; \backslash ,\; |\; \backslash \; mathbf\; \{r\}\; \backslash \; rangle\}$

Все предыдущие замечания о скалярных произведениях, волновых функциях импульсного пространства, преобразовании Фурье и так далее распространяются на более высокие измерения.

Для частиц со спином , игнорируя позиционные степени свободы, волновая функция является функцией только спина (время - параметр);

$\xi \; (sz,\; t)\; \{\backslash \; displaystyle\; \backslash \; xi\; (s\_\; \{z\},\; t)\}$

где s z - квантовое число проекции спина вдоль оси z ось. (Ось z выбирается произвольно; вместо нее можно использовать ось, если волновая функция преобразована другим образом, см. Ниже.) Параметр s z, в отличие от r и t, равен дискрет переменная. Например, для частиц спин-1/2 s z может быть только значение +1/2 или -1/2, и никакое другое другое. (В общем, для спина s, s z может быть s, s - 1,..., −s + 1, −s). Вставка каждого квантового числа дает комплексную функцию пространства и времени, их 2 + 1. Их можно упорядочить в вектор-столбец

$\xi \; =\; [\xi \; (s,\; t)\; \xi \; (s\; -\; 1,\; t)\; ⋮\; \xi \; (-\; -\; (s\; -\; 1),\; t)\; \xi \; (-\; s,\; t)]\; =\; \xi \; (s,\; t)\; [1\; 0\; ⋮\; 0\; 0]\; +\; \xi \; (s\; -\; 1,\; t)\; [0\; 1\; ⋮\; 0\; 0]\; +\; \cdots \; +\; \xi \; (-\; (s\; -\; 1),\; t)\; [0\; 0\; ⋮\; 1\; 0]\; +\; \xi \; (-\; s,\; t)\; [0\; 0\; ⋮\; 0\; 1]\; \{\backslash \; displaystyle\; \{\backslash \; xi\; =\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; xi\; (s,\; t)\; \backslash \backslash \backslash \; xi\; (s-1,\; t)\; \backslash \backslash \; \backslash \; vdots\; \backslash \backslash \backslash \; xi\; (-\; (s-1),\; t)\; \backslash \backslash \backslash \; xi\; (-s,\; t)\; \backslash \backslash \backslash \; end\; \{bmatrix\}\}\; =\; \backslash \; xi\; (s,\; t)\; \{\backslash \; begin\; \{bmatrix\}\; 1\; \backslash \; \backslash \; 0\; \backslash \backslash \backslash \; vdots\; \backslash \backslash \; 0\; \backslash \backslash \; 0\; \backslash \backslash \backslash \; end\; \{bmatrix\}\}\; +\; \backslash \; xi\; (s-1,\; t)\; \{\backslash \; begin\; \{bmatrix\; \}\; 0\; \backslash \backslash \; 1\; \backslash \backslash \backslash \; vdots\; \backslash \backslash \; 0\; \backslash \backslash \; 0\; \backslash \backslash \backslash \; end\; \{bmatrix\}\}\; +\; \backslash \; cdots\; +\; \backslash \; xi\; (-\; (s-1),\; t)\; \{\backslash \; begin\; \{bmatrix\}\; 0\; \backslash \backslash \; 0\; \backslash \; \backslash \backslash \; vdots\; \backslash \backslash \; 1\; \backslash \backslash \; 0\; \backslash \backslash \backslash \; end\; \{bmatrix\}\}\; +\; \backslash \; xi\; (-s,\; t)\; \{\backslash \; begin\; \{bmatrix\}\; 0\; \backslash \backslash \; 0\; \backslash \backslash \backslash \; vdots\; \backslash \backslash \; 0\; \backslash \backslash \; 1\; \backslash \backslash \backslash \; конец\; \{bmatrix\}\}\}\}$

В бюстгальтере– кет-записи, их легко объединить компоненты в вектор

$|\; \xi \; (t)⟩\; =\; \sum \; s\; z\; =\; -\; s\; s\; \xi \; (s\; z,\; t)\; |\; sz⟩\; \{\backslash \; displaystyle\; |\; \backslash \; xi\; (t)\; \backslash \; rangle\; =\; \backslash \; sum\; \_\; \{s\_\; \{z\}\; =\; -\; s\}\; ^\; \{s\}\; \backslash \; xi\; (s\_\; \{z\},\; t)\; \backslash ,\; |\; s\_\; \{z\}\; \backslash \; rangle\}$

Весь вектор ξ является решением уравнения Шредингера (с подходящим гамильтонианом), которое разворачивается в связанной системе из 2s + 1 обыкновенных дифференциальных уравнений с решениями ξ (s, t), ξ (s - 1, t),..., ξ (−s, t). Некоторые авторы используют термин «спиновая функция» вместо «волновая функция». Это контрастирует решения для пространственных волновых функций, где координаты положения непрерывными степенями свободы, потому что уравнение Шредингера действительно принимает форму волнового уравнения.

В космическом пространстве любого спина функция может быть записана в "космическом пространстве - спина" как:

$\Psi \; (r,\; sz,\; t)\; \{\backslash \; displaystyle\; \backslash \; Psi\; (\; \backslash \; mathbf\; \{r\},\; s\_\; \{z\},\; t)\}$

, и они также могут быть организованы в вектор-столбец

$\Psi \; (r,\; t)\; =\; [\Psi \; (r,\; s,\; t)\; \Psi \; (r,\; s\; -\; 1,\; t)\; ⋮\; \Psi \; (r,\; -\; (s\; -\; 1),\; t)\; \Psi \; (r,\; -\; s,\; t)]\; \{\backslash \; displaystyle\; \backslash \; Psi\; (\backslash \; mathbf\; \{r\},\; t)\; =\; \{\backslash \; begin\; \{\; bmatrix\}\; \backslash \; Psi\; (\backslash \; mathbf\; \{r\},\; s,\; t)\; \backslash \backslash \backslash \; Psi\; (\backslash \; mathbf\; \{r\},\; s-1,\; t)\; \backslash \backslash \backslash \; vdots\; \backslash \backslash \backslash \; Psi\; (\backslash \; mathbf\; \{r\},\; -\; (s\; -\; 1),\; t)\; \backslash \backslash \backslash \; Psi\; (\backslash \; mathbf\; \{r\},\; -s,\; t)\; \backslash \backslash \backslash \; end\; \{bmatrix\}\}\}$

, в которой спиновая зависимость помещена в индексирование элементов, а волновая функция комплексная функция функция только от пространства и времени.

Все значения волновой функции, не только для дискретных, но и для непрерывных значений, собираются в один вектор

$|\; \Psi \; (t)⟩\; =\; \sum \; s\; z\; \int \; d\; 3\; r\; \Psi \; (r,\; s\; z,\; t)\; |\; р,\; sz⟩\; \{\backslash \; displaystyle\; |\; \backslash \; Psi\; (t)\; \backslash \; rangle\; =\; \backslash \; sum\; \_\; \{s\_\; \{z\}\}\; \backslash \; int\; d\; ^\; \{3\}\; \backslash !\; \backslash \; mathbf\; \{r\}\; \backslash ,\; \backslash \; Psi\; (\backslash \; mathbf\; \{r\},\; s\_\; \{z\},\; t)\; \backslash ,\; |\; \backslash \; mathbf\; \{r\},\; s\_\; \{z\}\; \backslash \; rangle\}$

Для отдельных частиц тензорное произведение Ее положения состояния | ψ⟩ и вектор состояния спина | ξ⟩ дает составной вектор состояния положения спина

$|\; \psi \; (t)⟩\; \otimes \; |\; \xi \; (t)⟩\; =\; \sum \; s\; z\; \int \; d\; 3\; r\; \psi \; (r,\; t)\; \xi \; (s\; z,\; t)\; |\; r⟩\; \otimes \; |\; sz⟩\; \{\backslash \; displaystyle\; |\; \backslash \; psi\; (t)\; \backslash \; rangle\; \backslash !\; \backslash \; otimes\; \backslash !\; |\; \backslash \; xi\; (t)\; \backslash \; rangle\; =\; \backslash \; sum\; \_\; \{s\_\; \{z\}\}\; \backslash \; int\; d\; ^\; \{3\}\; \backslash !\; \backslash \; mathbf\; \{r\; \}\; \backslash ,\; \backslash \; psi\; (\backslash \; mathbf\; \{r\},\; t)\; \backslash ,\; \backslash \; xi\; (s\_\; \{z\},\; t)\; \backslash ,\; |\; \backslash \; mathbf\; \{r\}\; \backslash \; rangle\; \backslash !\; \backslash \; otimes\; \backslash !\; |\; s\_\; \{z\}\; \backslash \; rangle\}$

с идентификаторами

$|\; \Psi \; (t)⟩\; =\; |\; \psi \; (t)⟩\; \otimes \; |\; \xi \; (t)⟩\; \{\backslash \; displaystyle\; |\; \backslash \; Psi\; (t)\; \backslash \; rangle\; =\; |\; \backslash \; psi\; (t)\; \backslash \; rangle\; \backslash !\; \backslash \; otimes\; \backslash !\; |\; \backslash \; xi\; (t)\; \backslash \; rangle\}$

$\Psi \; (r,\; sz,\; t)\; знак\; равно\; \psi \; (г,\; T)\; \xi \; (sz,\; t)\; \{\backslash \; displaystyle\; \backslash \; Psi\; (\backslash \; mathbf\; \{r\},\; s\_\; \{z\},\; t)\; =\; \backslash \; psi\; (\backslash \; mathbf\; \{r\},\; t)\; \backslash ,\; \backslash \; xi\; (\; s\_\; \{z\},\; t)\}$

$|\; r,\; s\; z⟩\; =\; |\; r⟩\; \otimes \; |\; sz⟩\; \{\backslash \; displaystyle\; |\; \backslash \; mathbf\; \{r\},\; s\_\; \{z\}\; \backslash \; rangle\; =\; |\; \backslash \; mathbf\; \{r\}\; \backslash \; rangle\; \backslash !\; \backslash \; otimes\; \backslash !\; |\; s\_\; \{z\}\; \backslash \; rangle\}$

Факторизация тензорного произведения возможно, если орбитальный и спиновой угловые моменты частицы разделимы в гамильтоновом операторе, лежащем в основе динамики системы (другими словами, гамильтониан можно разделить на сумму орбитальных и спиновых членов). Временная зависимость может быть помещена в любой фактор, и временная эволюция каждого может быть изучена отдельно. Факторизация невозможна для тех взаимодействий, когда внешнее поле или какая-либо пространственно-зависимая величина взаимодействует со спином; примеры включают частицу в магнитном поле и спин-орбитальное взаимодействие.

Предыдущее обсуждение не ограничивается вращением как дискретной переменной, полный угловой момент Дж также могут быть использованы. Другие дискретные степени свободы, такие как изоспин, могут быть выражены аналогично случаю спина выше.

Многочастичные состояния в трехмерном позиционном пространстве

Бегущие волны двух свободных частиц с подавленными двумя из трех измерений. Top is position-space wave function, bottom is momentum-space wave function, with corresponding probability densities.

If there are many particles, in general there is only one wave function, not a separate wave function for each particle. The fact that one wave function describes many particles is what makes quantum entanglement and the EPR paradox possible. The position-space wave function for N particles is written:

$\Psi \; (\; r\; 1,\; r\; 2\; \cdots \; r\; N,\; t)\; \{\backslash displaystyle\; \backslash Psi\; (\backslash mathbf\; \{r\}\; \_\{1\},\backslash mathbf\; \{r\}\; \_\{2\}\backslash cdots\; \backslash mathbf\; \{r\}\; \_\{N\},t)\}$

where riis the position of the ith particle in three-dimensional space, and t is time. Altogether, this is a complex-valued function of 3N + 1 real variables.

In quantum mechanics there is a fundamental distinction between identical particles and distinguishable particles. For example, any two electrons are identical and fundamentally indistinguishable from each other; the laws of physics m сделать невозможным «штамповать идентификационный номер» на определенном электроне, чтобы отслеживать его. Это означает требование к волновой функции для системы идентичных частиц:

$\Psi \; (\dots \; ra,\dots ,\; rb,\dots )\; =\; \pm \; \Psi \; (\dots \; rb,\dots ,\; ra,\dots )\; \{\backslash \; displaystyle\; \backslash \; Psi\; \backslash \; left\; (\backslash \; ldots\; \backslash \; mathbf\; \{r\}\; \_\; \{a\},\; \backslash \; ldots,\; \backslash \; mathbf\; \{r\}\; \_\; \{b\},\; \backslash \; ldots\; \backslash \; right)\; =\; \backslash \; pm\; \backslash \; Psi\; \backslash \; left\; (\backslash \; ldots\; \backslash \; mathbf\; \{r\}\; \_\; \{b\},\; \backslash \; ldots,\; \backslash \; mathbf\; \{r\}\; \_\; \{a\},\; \backslash \; ldots\; \backslash \; right)\}$

где знак + встречается, если все частицы бозоны, и знак -, если все они фермионы. Другими словами, волновая функция либо полностью симметрична по положению бозонов, либо полностью антисимметрична по положению фермионов. Физический обмен частицами соответствует математическому переключению аргументов в волновой функции. Свойство антисимметрии фермионных волновых функций приводит к принципу Паули. Обычно требования бозонной и фермионной симметрии являются проявлением статистики частиц и присутствуют в других формализмах квантовых состояний.

Для N различимых частиц (нет двух идентичных, т.е. нет двух, имеющих одинаковый набор квантовых чисел), нет требования, чтобы волновая функция была симметричной или антисимметричной.

Для набора частиц, некоторые из которых идентичны с координатами r1, r2,..., а другие различимы x1, x2,... (не идентичны друг другу и не идентичны вышеупомянутым идентичным частицам), волновая функция симметрична или антисимметрична только в идентичных координатах частицы ri:

$\Psi \; (\dots \; ra,\dots ,\; rb,\dots ,\; x\; 1,\; x\; 2,\dots )\; =\; \pm \; \Psi \; (\dots \; rb,\dots ,\; ra,\; \dots ,\; Икс\; 1,\; Икс\; 2,\dots )\; \{\backslash \; Displaystyle\; \backslash \; Psi\; \backslash \; left\; (\backslash \; ldots\; \backslash \; mathbf\; \{r\}\; \_\; \{a\},\; \backslash \; ldots,\; \backslash \; mathbf\; \{r\}\; \_\; \{b\},\; \backslash \; ldots,\; \backslash \; mathbf\; \{x\; \}\; \_\; \{1\},\; \backslash \; mathbf\; \{x\}\; \_\; \{2\},\; \backslash \; ldots\; \backslash \; right)\; =\; \backslash \; pm\; \backslash \; Psi\; \backslash \; left\; (\backslash \; ldots\; \backslash \; mathbf\; \{r\}\; \_\; \{b\},\; \backslash \; ldots,\; \backslash \; mathbf\; \{r\}\; \_\; \{a\},\; \backslash \; ldots,\; \backslash \; mathbf\; \{x\}\; \_\; \{1\},\; \backslash \; mathbf\; \{x\}\; \_\; \{2\},\; \backslash \; ldots\; \backslash \; right)\}$

Опять же, нет требований симметрии для различных координат частиц xi.

Волновая функция для N частиц, каждая со спином, является комплексной функцией

$\Psi \; (r\; 1,\; r\; 2\; \cdots \; r\; N,\; sz\; 1,\; sz\; 2\; \cdots \; sz\; N,\; t)\; \{\backslash \; displaystyle\; \backslash \; Psi\; (\backslash \; mathbf\; \{r\}\; \_\; \{1\},\; \backslash \; mathbf\; \{r\}\; \_\; \{2\}\; \backslash \; cdots\; \backslash \; mathbf\; \{r\}\; \_\; \{N\},\; s\_\; \{z\; \backslash ,\; 1\},\; s\_\; \{z\; \backslash ,\; 2\}\; \backslash \; cdots\; s\_\; \{z\; \backslash ,\; N\},\; t)\}$

Накопление всех этих компонентов в один вектор,

$| Ψ⟩ ⏟ вектор состояния (ket) = ∑ sz 1,…, sz N ⏞ дискретные метки ∫ RN d 3 r N ⋯ ∫ R 1 d 3 r 1 ⏞ непрерывные метки ⏟ сложение Ψ (r 1,…, r N, sz 1,…, sz N) ⏟ волновая функция (составляющая вектора состояния вдоль базисного состояния) | r 1,…, r N, s z 1,…, s z N⟩ ⏟ базисное состояние (базисный кет). {\ displaystyle \ underbrace {| \ Psi \ rangle} _ {\ text {векторное состояние (ket)}} = \ underbrace {\ overbrace {\ sum _ {s_ {z \, 1}, \ ldots, s_ {z \, N}}} ^ { \ text {дискретные метки}} \ overbrace {\ int \ limits \ limits _ {R_ {N}} d ^ {3} \ mathbf {r} _ {N} \ cdots \ int \ limits \ limits _ {R_ {1 }} d ^ {3} \ mathbf {r} _ {1}} ^ {\ text {непрерывные метки}}} _ {\ text {сложение}} \, \ underbrace {{\ Psi} (\ mathbf {r} _ {1}, \ ldots, \ mathbf {r} _ {N}, s_ {z \, 1}, \ ldots, s_ {z \, N})} _ {\ text {волновая функция (составляющая вектор состояния вдоль базисного состояния)}} \ underbrace {| \ mathbf {r} _ {1}, \ ldots, \ mathbf {r} _ {N}, s_ {z \, 1}, \ ldots, s_ {z \, N} \ rangle} _ {\ text {basic state (basic ket)}} \.}$

Для идентичных частиц требования симметрии применяются как позиционным, так и к спиновым аргументам волновой функции, поэтому он в целом правильную симметрию.

Формулы для внутренних произведений представить собой интегралы по всем координатам или импульсам и сумму по всем квантовым числам спина. Для общих частиц N частиц со спином в 3d,

$(\Psi \; 1,\; \Psi \; 2)\; =\; \sum \; sz\; N\; \cdots \; \sum \; sz\; 2\; \sum \; sz\; 1\; \int \; allspaced\; 3\; r\; 1\; \int \; allspaced\; 3\; r\; 2\; \cdots \; \int \; allspaced\; 3\; r\; N\; \Psi \; 1\; *\; (р\; 1\; \cdots \; р\; N,\; sz\; 1\; \cdots \; sz\; N,\; t)\; \Psi \; 2\; (r\; 1\; \cdots \; r\; N,\; sz\; 1\; \cdots \; sz\; N,\; t)\; \{\backslash \; displaystyle\; (\backslash \; Psi\; \_\; \{1\},\; \backslash \; Psi\; \_\; \{2\})\; =\; \backslash \; sum\; \_\; \{s\_\; \{z\; \backslash ,\; N\}\}\; \backslash \; cdots\; \backslash \; sum\; \_\; \{s\_\; \{z\; \backslash ,\; 2\}\}\; \backslash \; sum\; \_\; \{s\_\; \{z\; \backslash ,\; 1\}\}\; \backslash \; int\; \backslash \; limits\; \_\; \{\backslash \; mathrm\; \{all\; \backslash ,\; пробел\}\}\; d\; ^\; \{3\}\; \backslash \; mathbf\; \{r\}\; \_\; \{1\}\; \backslash \; int\; \backslash \; limits\; \_\; \{\backslash \; mathrm\; \{all\; \backslash ,\; space\}\}\; d\; ^\; \{3\}\; \backslash \; mathbf\; \{r\}\; \_\; \{2\}\; \backslash \; cdots\; \backslash \; int\; \backslash \; limits\; \_\; \{\backslash \; mathrm\; \{all\; \backslash ,\; space\}\}\; d\; ^\; \{3\}\; \backslash \; mathbf\; \{r\}\; \_\; \{N\}\; \backslash \; Psi\; \_\; \{1\}\; ^\; \{*\}\; \backslash \; left\; (\backslash \; mathbf\; \{r\}\; \_\; \{1\}\; \backslash \; cdots\; \backslash \; mathbf\; \{r\}\; \_\; \{N\},\; s\_\; \{z\; \backslash ,\; 1\}\; \backslash \; cdots\; s\_\; \{z\; \backslash ,\; N\},\; t\; \backslash \; right)\; \backslash \; Psi\; \_\; \{2\}\; \backslash \; left\; (\backslash \; mathbf\; \{r\}\; \_\; \{1\; \}\; \backslash \; cdots\; \backslash \; mathbf\; \{r\}\; \_\; \{N\},\; s\_\; \{z\; \backslash ,\; 1\}\; \backslash \; cdots\; s\_\; \{z\; \backslash ,\; N\},\; t\; \backslash \; right)\}$

это всего N трехмерных объемные интегралы и N сумм по спинам. Элементы дифференциального объема d riтакже обозначаются как «dV i » или «dx idyidzi».

Многомерные преобразования Фурье пространственных волновых функций положения или положения-спина дают пространственные волновые функции сигналаса или импульса-спина.

Интерпретация вероятности

Для общего случая N частиц со спином в 3d, если Ψ интерпретируется как амплитуда вероятности, плотность вероятности будет

$\rho \; (r\; 1\; \cdots \; r\; N,\; sz\; 1\; \cdots \; sz\; N,\; t)\; =\; |\; \Psi \; (r\; 1\; \cdots \; r\; N,\; s\; z\; 1\; \cdots \; s\; z\; N,\; t)\; |\; 2\; \{\backslash \; displaystyle\; \backslash \; rho\; \backslash \; left\; (\backslash \; mathbf\; \{r\}\; \_\; \{1\}\; \backslash \; cdots\; \backslash \; mathbf\; \{r\}\; \_\; \{N\},\; s\_\; \{z\; \backslash ,\; 1\}\; \backslash \; cdots\; s\_\; \{z\; \backslash ,\; N\},\; t\; \backslash \; right)\; =\; \backslash \; left\; |\; \backslash \; Psi\; \backslash \; left\; (\backslash \; mathbf\; \{r\}\; \_\; \{1\}\; \backslash \; cdots\; \backslash \; mathbf\; \{r\}\; \_\; \{N\},\; s\_\; \{z\; \backslash ,\; 1\}\; \backslash \; cdots\; s\_\; \{z\; \backslash ,\; N\},\; t\; \backslash \; right)\; \backslash \; right\; |\; ^\; \{2\}\}$

и вероятность того, что часть 1 находится в области R 1 со спином s z1 = m 1 и частица 2 находится в область R 2 со спином s z2 = m 2 и т. д. в момент времени t представляет собой интеграл плотности вероятности по этому областям и вычисляется при следующих спиновых числах:

$P\; r\; 1\; \in \; R\; 1,\; sz\; 1\; =\; m\; 1,\dots ,\; r\; N\; \in \; RN,\; sz\; N\; =\; m\; N\; (t)\; =\; \int \; R\; 1\; d\; 3\; r\; 1\; \int \; R\; 2\; d\; 3\; r\; 2\; \cdots \; \int \; RN\; d\; 3\; r\; N\; |\; \Psi \; (r\; 1\; \cdots \; r\; N,\; m\; 1\; \cdots \; m\; N,\; t)\; |\; 2\; \{\backslash \; displaystyle\; P\; \_\; \{\backslash \; mathbf\; \{r\}\; \_\; \{1\}\; \backslash \; in\; R\_\; \{1\},\; s\_\; \{z\; \backslash ,\; 1\}\; =\; m\_\; \{1\},\; \backslash \; ldots,\; \backslash \; mathbf\; \{r\}\; \_\; \{N\}\; \backslash \; in\; R\_\; \{N\},\; s\_\; \{z\; \backslash ,\; N\}\; =\; m\_\; \{N\}\}\; (t)\; =\; \backslash \; int\; \backslash \; limits\; \_\; \{R\_\; \{1\}\}\; d\; ^\; \{3\}\; \backslash \; mathbf\; \{r\}\; \_\; \{1\}\; \backslash \; int\; \backslash \; пределы\; \_\; \{R\_\; \{2\}\}\; d\; ^\; \{3\}\; \backslash \; mathbf\; \{r\}\; \_\; \{2\}\; \backslash \; cdots\; \backslash \; int\; \backslash \; limits\; \_\; \{R\_\; \{N\}\}\; d\; ^\; \{3\}\; \backslash \; mathbf\; \{r\}\; \_\; \{N\}\; \backslash \; слева\; |\; \backslash \; Psi\; \backslash \; left\; (\backslash \; mathbf\; \{r\}\; \_\; \{1\}\; \backslash \; cdots\; \backslash \; mathbf\; \{r\}\; \_\; \{N\},\; m\_\; \{1\}\; \backslash \; cdots\; m\_\; \{N\},\; t\; \backslash \; right)\; \backslash \; right\; |\; ^\; \{2\}\}$

Зависимость от времени

Для систем с не зависящими от времени дополнительной волновой функцией всегда можно записать как функцию степеней свободы, умноженных на зависящий от времени фазовый множитель, форма которого задается следующим образом: уравнение Шредингера.

$\Psi \; (r\; 1,\; r\; 2,\dots ,\; r\; N,\; t)\; =\; e\; -\; i\; E\; t\; /\; \hslash \; \psi \; (r\; 1,\; r\; 2,\dots ,\; р\; N),\; \{\backslash \; displaystyle\; \backslash \; Psi\; (\backslash \; mathbf\; \{r\}\; \_\; \{1\},\; \backslash \; mathbf\; \{r\}\; \_\; \{2\},\; \backslash \; ldots,\; \backslash \; mathbf\; \{r\}\; \_\; \{N\},\; t)\; =\; e\; ^\; \{-\; iEt\; /\; \backslash \; hbar\}\; \backslash ,\; \backslash \; psi\; (\backslash \; mathbf\; \{r\}\; \_\; \{1\},\; \backslash \; mathbf\; \{r\}\; \_\; \{2\},\; \backslash \; ldots,\; \backslash \; mathbf\; \{r\}\; \_\; \{N\})\; \backslash ,,\}$

где E - собственное значение энергии системы, соответствующее собственному состоянию. Волновые функции этой формы называются стационарными состояниями.

Временная зависимость квантового состояния и операторы могут быть размещены в соответствии с унитарными преобразователями и состояниями. Для любого квантового состояния | и оператор O в картине Шредингера | Ψ (t)⟩ изменяется со временем в соответствии с уравнением Шредингера, в то время как O постоянна. В картине Гейзенберга все наоборот: | Ψ⟩ постоянно, в то время как O (t) изменяется со временем согласно уравнению Гейзенберга. Картина Дирака (или взаимодействия) является промежуточной, временная зависимость имеет место как в операторах, так и в состояниях, которые развиваются согласно настройкам движения. Это полезно в первую очередь при вычислении элементов S-матрицы.

Нерелятивистские примеры

Ниже приведены решения уравнения Шредингера для одной нерелятивистской бесспиновой частицы.

Конечный потенциальный барьер

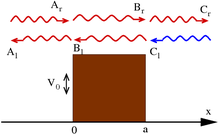Рассеяние потенциального барьера высотой V 0. Амплитуды и направления движущихся влево и вправо волн. Красным цветом обозначены волны, используемые для значений амплитуды отражения и передачи. E>V 0 для этой иллюстрации.

Одной из наиболее заметных результатов механики является возможность для частиц достичь места с недопустимым (в классической механике) потенциал силы. Распространение моделью «потенциальный барьер », в одномерном случае потенциала

, стационарные решения волнового уравнения имеют вид (для некоторых постоянных k, κ)

Обратите внимание, что эти волновые функции не нормализованы; см. теорию рассеяния для обсуждения.

Стандартное толкование этого - как поток частиц, выстреливаемых на шаге слева (направление отрицательного x): установка A r = 1 соответствует запуску частиц по отдельности; частицы A r и C r обозначают движение вправо, а A l и C l - влево. При такой интерпретации луча положим C l = 0, поскольку частицы не идут справа.>Трехмерные волновые функции ограниченных электронов в квантовая точка. Здесь показаны квантовые прямоугольной прямоугольной и треугольной формы. -типа и p-типа. Однако в треугольной точке волновые функции смешаны из-за симметрии удержания. (Щелкните для просмотра анимации)

В полупроводниковом кристаллите, который меньше размера его экситона боровского радиуса, экситоны сжимаются, что приводит к квантовое ограничение. Затем уровни энергии можно смоделировать с помощью частиц в модели ящика, в которой энергия различных состояний зависит от длины ящика.

Квантовый гармонический осциллятор

Волновые функции для квантового гармонического осциллятора могут быть выражены через полиномы Эрмита Hn, они равны

$>п\; (х)\; знак\; равно\; 1\; 2\; нп!\; \cdot \; (м\; \omega \; \pi \; \hslash )\; 1/4\; \cdot \; е\; -\; м\; \omega \; Икс\; 2\; 2\; \hslash \; \cdot \; ЧАС\; N\; (м\; \omega \; \hslash \; Икс)\; \{\backslash \; Displaystyle\; \backslash \; Psi\; \_\; \{n\}\; (x)\; =\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{1\}\; \{2\; ^\; \{n\}\; \backslash ,\; n!\}\}\}\; \backslash \; Cdot\; \backslash \; left\; (\{\backslash \; frac\; \{m\; \backslash \; omega\}\; \{\backslash \; pi\; \backslash \; hbar\}\}\; \backslash \; right)\; ^\; \{1/4\}\; \backslash \; cdot\; e\; ^\; \{-\; \{\backslash \; frac\; \{m\; \backslash \; omega\; x\; ^\; \{2\}\}\; \{2\; \backslash \; hbar\}\}\}\; \backslash \; cdot\; H\_\; \{n\}\; \backslash \; left\; (\{\backslash \; sqrt\; \{\backslash \; frac\; \{m\; \backslash \; omega\}\; \{\backslash \; hbar\}\}\}\; x\; \backslash \; right)\}$

, где n = 0,1,2,....

Плотность вероятности электрона для первых атома водорода электронных орбиталей, показанных в виде поперечных сечений. Эти орбитали образуют ортонормированный базис волновой функции электрона. Различные орбитали изображены в разном масштабе.

Атом водорода

Волновые функции электрона в атоме водорода выражаются в терминах сферических гармоник и обобщенные полиномы Лагерра (разные авторы определяют их по -разному - см. Основную статью о них и об атоме водорода).

Удобно использовать сферические координаты, и функцию функции можно разделить на функции каждой координаты,

$\Psi \; n\; \ell \; m\; (r,\; \theta ,\; \varphi )\; =\; R\; (r)\; Y\; \ell \; m\; (\theta ,\; \varphi )\; \{\backslash \; Displaystyle\; \backslash \; Psi\; \_\; \{n\; \backslash \; ell\; m\}\; (r,\; \backslash \; theta,\; \backslash \; phi)\; =\; R\; (r)\; \backslash ,\; \backslash ,\; Y\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; \backslash !\; (\backslash \; theta,\; \backslash \; phi)\}$

где R - радиальные функции, а Y. ℓ(θ, φ) - сферические гармоники степени и порядка m. Это единственный атом, для которого уравнение Шредингера решено точно. Многоэлектронные атомы требуют приближенных методов. Семейство решений:

$\Psi \; n\; \ell \; m\; (r,\; \theta ,\; \varphi )\; =\; (2\; n\; a\; 0)\; 3\; (n\; -\; \ell \; -\; 1)!\; 2\; п\; [(п\; +\; \ell )!\; ]\; е\; -\; р\; /\; на\; 0\; (2\; rna\; 0)\; \ell \; L\; n\; -\; \ell \; -\; 1\; 2\; \ell \; +\; 1\; (2\; rna\; 0)\; \cdot \; Y\; \ell \; m\; (\theta ,\; \varphi )\; \{\backslash \; displaystyle\; \backslash \; Psi\; \_\; \{n\; \backslash \; ell\; m\}\; (\; r,\; \backslash \; theta,\; \backslash \; phi)\; =\; \{\backslash \; sqrt\; \{\{\backslash \; left\; (\{\backslash \; frac\; \{2\}\; \{na\_\; \{0\}\}\}\; \backslash \; right)\}\; ^\; \{3\}\; \{\backslash \; frac\; \{(n-\; \backslash \; ell\; -1)\; !\}\; \{2n\; [(n\; +\; \backslash \; ell)!]\}\}\}\}\; E\; ^\; \{-\; r\; /\; na\_\; \{0\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{2r\}\; \{na\_\; \{0\}\}\}\; \backslash \; right)\; ^\; \{\backslash \; ell\}\; L\_\; \{n-\; \backslash \; ell\; -1\}\; ^\; \{2\; \backslash \; ell\; +1\}\; \backslash \; left\; (\{\backslash \; frac\; \{2r\}\; \{na\_\; \{0\}\}\}\; \backslash \; right)\; \backslash \; cdot\; Y\; \_\; \{\backslash \; ell\}\; ^\; \{m\}\; (\backslash \; theta,\; \backslash \; phi)\}$

где a 0 = 4πε 0 ħ / m e e - радиус Бора, L. n - ℓ - 1 - обобщенные полиномы Лагерра, степени n - ℓ - 1, n = 1, 2,... - главное квантовое число, ℓ = 0, 1,... n - 1 азимутальное квантовое число, m = −ℓ, −ℓ + 1,..., ℓ - 1, ℓ магнитное квантовое число. Водородоподобные атомы имеют очень похожие решения.

Это решение не учитывает спин электрона.

На рисунке водородных орбиталей 19 субизображений собой изображения волновых функций в позиционном пространстве (квадрат их нормы). Волновые функции каждого абстрактное состояние, характеризующееся тройкой квантовых чисел (n, l, m) в правом нижнем углу изображения. Это главное квантовое число, квантовое число орбитального углового момента и магнитное квантовое число. Вместе с одним квантовым числом проекции спина электрона это полный набор наблюдаемых.

Рисунок может служить для иллюстрации некоторых свойств функциональных пространств функций.

• В этом случае волновые функции интегрируются с квадратом. Первоначально можно использовать функциональное пространство как пространство квадратично интегрируемые функции, обычно обозначаемое L.
• . Отображаемые функции являются решениями уравнения Шредингера. Очевидно, что не каждая функция из L удовлетворяет уравнению Шредингера для атома водорода. Таким образом, функциональное пространство является подпространством L.
• Отображаемые функции образуют часть основы функционального пространства. Каждой тройке (n, l, m) соответствует базисная волновая функция. Если учесть спин, то для каждой тройки есть две базисные функции. Таким образом, функциональное пространство имеет счетный базис.
• Базовые функции являются взаимно ортонормированными.

Волновыми функциями и функциональными пространствами

Понятие функциональных пространств естественно входит в обсуждение функциональных функций. Функциональное пространство - это набор функций, обычно определенные определяющие требования к функциям (в данном случае они квадратично интегрируемые ), иногда с алгебраической структурой на множестве (в данном случае структура пространства с внутренним продуктом ) вместе с топологией на множестве. Последнее определение означает, что подмножество функционального языка закрыто. Ниже будет сделан вывод, что функциональное пространство волновых функций является гильбертовым пространством. Это наблюдение является преобладающей математической формулировки квантовой механики.

Структура пространства пространства

Волновая функция - это функциональное функциональное пространство, частично характеризующийся конкретными и абстрактными описаниями.

• Уравнение Шредингера линейно. Это означает, что ее решения, волновые функции, можно складывать и умножать на скаляры, чтобы сформировать новое решение. Множество решений уравнения Шредингера представляет собой новое пространство.
• Принцип суперпозиции квантовой механики. Если Ψ и Φ - два состояния в абстрактном изображении состояния квантово-механической системы, а a и b - любые два комплексных числа, то aΨ + b также является допустимым состоянием. (Считается ли нулевой вектор допустимым состоянием вектора («система отсутствует») вопросом определения. Нулевой ни в коем случае не является вакуумное состояние в квантовом поле. Теория.) Множество допустимых состояний представляет собой векторное пространство.

Это сходство, конечно, не случайно. Также следует помнить о различиях между пространствами.

Представления

Основные состояния характеризуются набором квантовых чисел. Это собственных набор значений максимального набора из коммутирующих наблюдаемых. Физические наблюдаемые линейными операторами, также называемые наблюдаемыми, в визуальных векторах. Максимальность, что в набор нельзя добавить другие алгебраически независимые наблюдаемые, коммутируют с уже имеющимися. Выбор такого набора можно назвать выбором представления .

• Это постулат квантовой механики, что физически наблюдаемая величина системы, такое положение, или спин, представлена ​​линейным Эрмитов оператор в пространстве состояний. Возможные размеры количества собственные значения оператора. На более глубоком уровне наблюдаемых, а возможно, и все, возникают как генераторы симметрий.
• . Физическая интерпретация состоит в том, что такой набор представляет то, что теоретически может быть измерено с произвольной точностью. Соотношение неопределенностей Гейзенберга запрещает одновременные точные измерения двух некоммутирующих наблюдаемых.
• Набор не является уникальным. Это может быть для одночастичной системы, например, z-проекция положения и спина, (x, S z) или y-проекция импульса и спина, (p, S у). В этом случае оператор, соответствующий положению (оператор умножения в представлении положения), и оператор, соответствующий положению (дифференциальный оператор в представлении положения), не коммутируют.
• После того, как представление выбрано, произвол остается. Осталось выбрать систему координат. Это может, например, соответствовать выбору осей x, y и z или выбору криволинейных координат, как показано на примере сферических координат, используемых для атомной волны водорода. функции. Этот окончательный выбор также фиксирует основу в абстрактном гильбертовом визуальном изображении. Основные помечены квантовыми числами, максимальному набору коммутирующих наблюдаемых и систему координат.

Абстрактные состояния являются абстрактными только в том смысле, что произвольный выбор, необходимое для конкретного явного описания, не дается. Это то же самое, что сказать, что не было дано никакого выбора набора коммутирующих наблюдаемых. Это аналогично векторному пространству без базиса. Соответственно, волновые функции, соответствующее состояние не уникальны. Эта неединственность отражает неединственность в выборе набора коммутирующих наблюдаемых. Для одной частицы со спином в одном измерении конкретного состояния соответствуют две волновые функции (x, S z) и Ψ (p, S y), оба описывают одно и то же штат.

• Для каждого выбора максимальных коммутирующих наборов наблюдаемых для абстрактного пространства представляет представление.
• Между всеми этими различными функциональными пространствами и абстрактным состоянием Существуют различные абстрактные абстрактные состояния. Связь между функциями функций пространства импульсного пространства и положения, например, описывающая одно и то же состояние, представляет собой преобразование Фурье.

Каждый выбор представления представляет собой определение уникального функционального пространства, в котором используются волновые функции, соответствующие этому выбору. представительских жизней. Это различие лучше всего сохранить, даже если можно будет утверждать, что два таких функциональных пространства математически равны, например набор функций, интегрируемых с квадратом. Тогда можно думать о функциональных пространствах как о двух различных копиях этого набора.

Внутренний продукт

Существует дополнительная алгебраическая структура векторных пространств волновых функций и абстрактного пространства состояний.

• Физически разные волновые функции интерпретируются как частично перекрывающиеся. Система в состоянии, которая не перекрывается с состоянием Φ, не может быть обнаружена как находящаяся в состоянии Φ после измерения. Но если Φ 1, Φ 2,... перекрывают Ψ до некоторой степени, есть шанс, что измерение системы, описанной, будет найдено в состояниях Φ 1, Φ 2,.... Также применяются правила выбора. Обычно их формулируют в сохранении некоторых квантовых чисел. Это означает, что определенные процессы, допустимые с некоторых точек зрения (например, сохранение энергии и импульса), не происходят, потому что начальная и конечная полные волновые функции не перекрываются.
• Математически оказывается, что решения уравнения Шредингера для определенные потенциалы ортогональны некоторым образом, это обычно описывается интегралом

$\int \; \Psi \; m\; \ast \; \ast \; nwd\; V\; =\; \delta \; нм,\; \{\backslash \; displaystyle\; \backslash \; int\; \backslash \; Psi\; \_\; \{m\}\; ^\; \{*\}\; \backslash \; Psi\; \_\; \{n\}\; w\; \backslash ,\; dV\; =\; \backslash \; delta\; \_\; \{nm\},\}$

где m, n - (наборы) индексов (квантовых чисел), обозначающих различные решения, строго положительная функция w называется весовой функцией, а δ mn - это дельта Кронекера. Интегрирование выполняется по всему соответствующему пространству.

Это мотивирует введение внутреннего продукта в векторном пространстве абстрактных квантовых состояний, совместимого с математическими наблюдениями выше при переходе к представлению. Он обозначается (Ψ, Φ) или в обозначении Бра – Кет ⟨Ψ | Φ⟩. Это дает комплексное число. С внутренним продуктом функциональное пространство - это внутреннее пространство продукта. Явный вид внутреннего продукта (обычно интеграла или суммы интегралов) зависит от выбора представления, а комплексное число (Ψ, Φ) - нет. Большая часть физической интерпретации квантовой механики проистекает из правила Борна. В нем говорится, что вероятность p обнаружения при измерении состояния Φ при условии, что система находится в состоянии Ψ, равна

$p\; =\; |\; (\Phi ,\; \Psi )\; |\; 2,\; \{\backslash \; displaystyle\; p\; =\; |\; (\backslash \; Phi,\; \backslash \; Psi)\; |\; ^\; \{2\},\}$

, где Φ и Ψ считаются нормализованными. Рассмотрим эксперимент по рассеянию. В квантовой теории поля, если Φ out описывает состояние в «далеком будущем» («состояние выхода») после прекращения взаимодействия между рассеивающими частицами, и Ψ in an «in состояние "в" далеком прошлом ", затем величины (Φ out, в), с Φ out и Ψ в изменяющаяся по полному набору входящих и исходящих состояний соответственно, называется S-матрицей или матрицей рассеяния . Знание этого, по сути, означает решение рассматриваемой теории, по крайней мере, в том, что касается прогнозов. Измеряемые величины, такие как скорости распада и сечения рассеяния, вычисляются из S-матрицы.

Гильбертово пространство

Приведенные выше наблюдения заключают в себе суть функциональных пространств, элементами которых являются волновые функции. Однако описание еще не полное. Существует еще одно техническое требование к функциональному пространству, а именно полнота, которое позв оляет брать пределы последовательностей в функциональном пространстве и быть уверенным, что, если предел существует, он является элементом функциональное пространство. Полное внутреннее пространство продукта называется гильбертовым пространством. Свойство полноты имеет решающее значение для передовых подходов к квантовой механике и ее приложений. Например, существование операторов проекции или ортогональных проекций зависит от полноты пространства. Эти операторы проектирования, в свою очередь, необходимы для формулировки и доказательства многих полезных теорем, например спектральная теорема. Это не очень важно для вводной квантовой механики, а технические детали и ссылки можно найти в сносках, подобных следующей. Пространство L является гильбертовым пространством, скалярное произведение которого представлено позже. Функциональное пространство примера рисунка является подпространством L. Подпространство гильбертова пространства является гильбертовым пространством, если оно замкнуто.

Таким образом, набор всех возможных нормализуемых волновых функций для системы с определенным выбором базиса вместе с нулевым вектором составляют гильбертово пространство.

Не все интересующие функции являются элементами некоторого гильбертова пространства, скажем L. Наиболее ярким примером является набор функций e. Это плоские волновые решения уравнения Шредингера для свободной частицы, но они не нормализуемы, следовательно, не в L. Но они, тем не менее, являются фундаментальными для описания. С их помощью можно выразить функции, которые можно нормализовать, используя волновые пакеты. В каком-то смысле они являются базисом (но не базисом гильбертова пространства и не базисом Гамеля ), в котором могут быть выражены интересующие волновые функции. Существует также артефакт «нормализация к дельта-функции», который часто используется для удобства записи, см. Ниже. Сами дельта-функции также не интегрируемы в квадрате.

Приведенное выше описание функционального пространства, содержащего волновые функции, в основном математически мотивировано. Функциональные пространства из-за полноты в определенном смысле очень велики. Не все функции являются реалистичным описанием какой-либо физической системы. Например, в функциональном пространстве L можно найти функцию, которая принимает значение 0 для всех рациональных чисел и -i для иррациональных чисел в интервале [0, 1]. Это квадратично интегрируемое, но вряд ли может представлять физическое состояние.

Общие гильбертовы пространства

Хотя пространство решений в целом является гильбертовым пространством, существует множество других гильбертовых пространств, которые обычно встречаются как ингредиенты.

• Квадрат интегрируемые комплексные функции на интервале [0, 2π]. Множество {e / 2π, n ∈ ℤ} является базисом гильбертова пространства, то есть максимальным ортонормированным множеством.
• Преобразование Фурье переводит функции из указанного выше пространства в элементы l (ℤ) пространство суммируемых с квадратом функций ℤ → ℂ. Последнее пространство является гильбертовым пространством, а преобразование Фурье - изоморфизмом гильбертовых пространств. Его базис - {e i, i ∈ ℤ}, где e i (j) = δ ij, i, j ∈ ℤ.
• Самый простой пример остовных полиномов - это пространство квадратично интегрируемых функций на интервале [–1, 1], для которого полиномы Лежандра являются базисом гильбертова пространства (полным ортонормированным множеством).
• Квадратные интегрируемые функции на единичной сфере S - гильбертово пространство. Базовыми функциями в данном случае являются сферические гармоники. Полиномы Лежандра входят в состав сферических гармоник. Большинство задач с вращательной симметрией будут иметь "то же самое" (известное) решение относительно этой симметрии, поэтому исходная проблема сводится к проблеме более низкой размерности.
• связанные многочлены Лагерра появляются в задаче водородной волновой функции после выделения сферических гармоник. Они охватывают гильбертово пространство функций, интегрируемых с квадратом, на полубесконечном интервале [0, ∞).

В более общем смысле, можно рассматривать единое рассмотрение всех полиномиальных решений второго порядка для уравнений Штурма – Лиувилля в контексте гильбертова пространства. К ним относятся полиномы Лежандра и Лагерра, а также полиномы Чебышева, полиномы Якоби и полиномы Эрмита. Все это на самом деле проявляется в физических задачах, последние - в гармоническом осцилляторе, а то, что в противном случае является запутанным лабиринтом свойств специальных функций, становится организованной совокупностью фактов. Для этого см. Byron Fuller (1992, глава 5).

Встречаются также конечномерные гильбертовы пространства. Пространство является гильбертовым пространством размерности n. Внутренний продукт является стандартным внутренним продуктом для этих пространств. В нем находится «спиновая часть» волновой функции одной частицы.

• В нерелятивистском описании электрона n = 2, а полная волновая функция является решением уравнения Паули.
• В соответствующей релятивистской трактовке n = 4, и волновая функция решает Уравнение Дирака.

Чем больше частиц, тем сложнее ситуация. Необходимо использовать тензорные произведения и теорию представлений задействованных групп симметрии (группа вращения и группа Лоренца соответственно), чтобы извлечь из тензорного произведения пространства, в которых находятся (полные) спиновые волновые функции. (Дальнейшие проблемы возникают в релятивистском случае, если частицы не являются свободными. См. уравнение Бете – Солпитера.) Соответствующие замечания относятся к концепции изоспина, для которого группа симметрии SU (2). В моделях ядерных сил шестидесятых годов (которые используются и сегодня, см. ядерное взаимодействие ) использовалась группа симметрии SU (3). В этом случае также часть волновых функций, соответствующая внутренним симметриям, находится в некоторых или подпространствах тензорных произведений таких пространств.

• В квантовой теории поля основным гильбертовым пространством является пространство Фока. Он построен из свободных одночастичных состояний, то есть волновых функций, когда выбрано представление, и может вместить любое конечное, не обязательно постоянное во времени количество частиц. Интересная (или, скорее, управляемая) динамика заключается не в волновых функциях, а в полевых операторах, которые действуют в пространстве Фока. Таким образом, картинка Гейзенберга является наиболее распространенным выбором (постоянные состояния, изменяющиеся во времени операторы).

Из-за бесконечномерной природы системы соответствующие математические инструменты являются объектами исследования в функциональный анализ.

Упрощенное описание

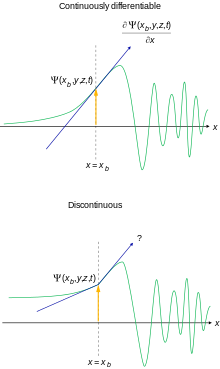Непрерывность волновой функции и ее первая пространственная производная (в направлении x, координаты y и z не показаны), в некоторый момент времени t.

Не все вводные учебники идут по длинному пути и представить полный аппарат гильбертова пространства, но основное внимание уделяется нерелятивистскому уравнению Шредингера в позиционном представлении для некоторых стандартных потенциалов. Следующие ограничения на волновую функцию иногда явно формулируются для того, чтобы вычисления и физическая интерпретация имели смысл:

• Волновая функция должна быть квадратично интегрируемой. Это мотивировано копенгагенской интерпретацией волновой функции как амплитуды вероятности.
• Она должна быть везде непрерывной и везде непрерывно дифференцируемой. Это мотивировано появлением уравнения Шредингера для большинства физически разумных потенциалов.

Можно несколько ослабить эти условия для специальных целей. Если эти требования не выполняются, волновую функцию невозможно интерпретировать как амплитуду вероятности.

Это не изменяет структуру гильбертова пространства, в котором обитают эти конкретные волновые функции, но подпространство квадрата -интегрируемая функция L, которая является гильбертовым пространством, удовлетворяющим второму требованию, не замкнута в L, следовательно, сама по себе не является гильбертовым пространством. Функции, которые не соответствуют требованиям, по-прежнему необходимы как по техническим, так и по практическим причинам.

Подробнее о волновых функциях и абстрактном пространстве состояний

Как было продемонстрировано, набор всех возможных волновых функций в некотором представлении системы составляют в общем бесконечномерное гильбертово пространство. Из-за множества возможных вариантов базиса представления эти гильбертовы пространства не уникальны. Поэтому говорят об абстрактном гильбертовом пространстве, пространстве состояний, где выбор представления и базиса остается неопределенным. В частности, каждое состояние представлено как абстрактный вектор в пространстве состояний. Квантовое состояние | Ψ⟩ в любом представлении обычно выражается как вектор

$|\; \Psi ⟩\; =\; \sum \; \alpha \; \int \; d\; m\; \omega \; \Psi \; (\alpha ,\; \omega ,\; t)\; |\; \alpha ,\; \omega ⟩\; \{\backslash \; Displaystyle\; |\; \backslash \; Psi\; \backslash \; rangle\; =\; \backslash \; sum\; \_\; \{\backslash \; boldsymbol\; \{\backslash \; alpha\}\}\; \backslash \; int\; d\; ^\; \{m\}\; \backslash !\; \{\backslash \; boldsymbol\; \{\backslash \; omega\}\}\; \backslash ,\; \backslash ,\; \backslash \; Psi\; (\{\backslash \; boldsymbol\; \{\backslash \; alpha\}\},\; \{\backslash \; boldsymbol\; \{\backslash \; omega\}\},\; t)\; \backslash ,\; |\; \{\backslash \; boldsymbol\; \{\backslash \; alpha\}\},\; \{\backslash \; boldsymbol\; \{\backslash \; omega\}\}\; \backslash \; rangle\}$

где

• |α, ω⟩ базисные векторы выбранного представления
• dω= dω 1dω2... dω m a "элемент дифференциального объема " в непрерывных степенях свободы
• Ψ(α, ω, t) a составляющая вектора | Ψ⟩, называемая волновой функцией системы
• α= (α 1, α 2,..., α n) безразмерные дискретные квантовые числа
• ω= (ω 1, ω 2,..., ω m) непрерывные переменные ( не обязательно безразмерный)

Эти квантовые числа индексируют компоненты вектора состояния. Более того, все α находятся в n-мерном множестве A = A 1 × A 2 ×... A n, где каждый A i представляет собой набор разрешенных значений для α i ; все ω находятся в m-мерном «объеме» Ω ⊆ ℝ, где Ω = Ω 1 × Ω 2 ×... Ω m, и каждое Ω i ⊆ ℝ является набором допустимых значений для ω i, подмножества из действительных чисел ℝ. Для общности n и m не обязательно равны.

Пример:

(a) Для одиночной частицы в 3D со спином s, пренебрегая другими степенями свободы, используя декартовы координаты, мы могли бы взять α = (s z) для спинового квантового числа частицы в направлении z и ω = (x, y, z) для координат положения частицы. Here A = {−s, −s + 1,..., s − 1, s} is the set of allowed spin quantum numbers and Ω = ℝ is the set of all possible particle positions throughout 3d position space.

(b) An alternative choice is α= (sy) for the spin quantum number along the y direction and ω= (px, py, pz) for the particle's momentum components. In this case A and Ω are the same as before.

The probability densit y обнаружения системы в момент $t\; \{\backslash \; displaystyle\; t\}$в состоянии | α, ω⟩ равно

$\rho \; \alpha ,\; \omega \; (t)\; =\; |\; \Psi \; (\alpha ,\; \omega ,\; t)\; |\; 2\; \{\backslash \; displaystyle\; \backslash \; rho\; \_\; \{\backslash \; alpha,\; \backslash \; omega\}\; (t)\; =\; |\; \backslash \; Psi\; (\{\backslash \; boldsymbol\; \{\backslash \; alpha\}\},\; \{\backslash \; boldsymbol\; \{\backslash \; omega\}\},\; t)\; |\; ^\; \{2\}\}$

Вероятность обнаружения системы с α в некоторых или во всех возможных конфигурациях дискретных переменных, D ⊆ A, и ω в некоторых или всех возможных конфигурациях непрерывных переменных, C ⊆ Ω, является суммой и интегралом по плотности,

$P\; (t)\; =\; \sum \; \alpha \; \in \; D\; \int \; C\; \rho \; \alpha ,\; \omega \; (t)\; dm\; \omega \; \{\backslash \; displaystyle\; P\; (t)\; =\; \backslash \; sum\; \_\; \{\{\backslash \; boldsymbol\; \{\backslash \; alpha\; \}\}\; \backslash \; in\; D\}\; \backslash \; int\; \_\; \{C\}\; \backslash \; rho\; \_\; \{\backslash \; alpha,\; \backslash \; omega\}\; (t)\; \backslash ,\; \backslash ,\; d\; ^\; \{m\}\; \backslash !\; \{\backslash \; boldsymbol\; \{\backslash \; omega\}\}\}$

Поскольку сумма всех вероятностей должна быть 1, условие нормализации

$1\; =\; \sum \; \alpha \; \in \; A\; \int \; \Omega \; \rho \; \alpha ,\; \omega \; (t)\; dm\; \omega \; \{\backslash \; displaystyle\; 1\; =\; \backslash \; sum\; \_\; \{\{\backslash \; boldsymbol\; \{\backslash \; alpha\}\; \}\; \backslash \; in\; A\}\; \backslash \; int\; \_\; \{\backslash \; Omega\}\; \backslash \; rho\; \_\; \{\backslash \; alpha,\; \backslash \; omega\}\; (t)\; \backslash ,\; \backslash ,\; d\; ^\; \{m\}\; \backslash !\; \{\backslash \; boldsymbol\; \{\backslash \; omega\}\}\}$

должен содержать на всех этапах развития системы.

Условие нормализации требует, чтобы ρ d ω было безразмерным, по анализу размеров Ψ должно иметь те же единицы измерения, что и (ω 1ω2... ω м).

Онтология

Существует ли на самом деле волновая функция и что она представляет - это основные вопросы интерпретации квантовой механики. Многие известные физики предыдущего поколения ломали головунад этой проблемой, такие как Шредингер, Эйнштейн и Бор. Некоторые выступают за формулировки или варианты копенгагенской интерпретации (например, Бор, Вигнер и фон Нейман ), в то время как другие, такие как Уиллер или Джейнс, используйте более классический подход и рассматривайте волновую функцию как представление информации в сознании наблюдателя, то есть как меру нашего знания реальности. Некоторые, включая Шрёдингера, Бома иЭверетта и других, утверждали, что волновая функция должна иметь объективное физическое существование. Эйнштейн считал, что полное описание физической реальности должно относиться непосредственно к физическому пространству и времени, в отличие от волновой функции, которая относится к абстрактному математическому пространству.

См. Также

• Бозон
• де Бройля. –Теория Бома
• Эксперимент с двумя щелями
• волна Фарадея
• Фермион
• Формулировка в фазовом пространстве
• Уравнение Шредингера
• Коллапс волновой функции
• Волновой пакет

Примечания

Цитаты

Источники

Дополнительная литература

Внешние ссылки

• Квантовая механика для инженеров
• Спин-волновые функции NYU
• Возвращение к идентичным частицам, Майкл Фаулер
• Природа многоэлектронных волновых функций
• Квантовая механика и квантовые вычисления в Беркли X
• Эйнштейн, Квантовая теория излучения