Отображение, сохраняющее операции сложения и скалярного умножения
В математике, линейное отображение (также называемое линейным отображением, линейным преобразованием или, в некоторых контекстах, линейной функцией ) - это отображение V → W между двумя модулями (например, двумя векторными пространствами ), который сохраняет (в смысле, определенном ниже) операции сложения и скалярного умножения. Если линейное отображение является биекцией, тогда оно называется линейным изоморфизмом .
. Важным частным случаем является когда V = W, и в этом случае линейное отображение называется (линейным) эндоморфизм V. Иногда термин линейный оператор относится к этому случаю. Согласно другому соглашению линейный оператор позволяет V и W различаться, требуя, чтобы они были действительными векторными пространствами. Иногда термин линейная функция имеет то же значение, что и линейное отображение, тогда как в аналитической геометрии это не так.
Линейное отображение всегда отображает линейные подпространства на линейные подпространства (возможно, более низкого измерения ); например, он отображает плоскость через исходную точку в плоскость, прямую линию или точку. Линейные карты часто могут быть представлены как матрицы, а простые примеры включают в себя линейные преобразования вращения и отражения.
На языке абстрактной алгебры линейная карта - это гомоморфизм модулей. На языке теории категорий, это морфизм в категории модулей над данным кольцом.
Содержание
- 1 Определение и первые следствия
- 2 Примеры
- 3 Матрицы
- 3.1 Примеры матриц линейного преобразования
- 4 Формирование новых линейных отображений из заданных
- 5 Эндоморфизмы и автоморфизмы
- 6 Ядро, образ и ранг –Теорема пустоты
- 7 Cokernel
- 8 Алгебраические классификации линейных преобразований
- 9 Изменение базиса
- 10 Непрерывность
- 11 Приложения
- 12 См. Также
- 13 Примечания
- 14 Библиография
Определение и первые следствия
Пусть V и W - векторные пространства над одним и тем же полем K. Функция f: V → W называется линейным отображением, если для любых двух векторов  и любой скаляр c ∈ K выполняются следующие два условия:
и любой скаляр c ∈ K выполняются следующие два условия:
 | аддитивность / операция сложения |
 | однородность степени 1 / операция скалярного умножения |
Таким образом, линейное отображение называется сохраняющим операцию. Другими словами, не имеет значения, применяется ли линейная карта до (правые части приведенных выше примеров) или после (левые части примеров) операций сложения и скалярного умножения.
По ассоциативность операции сложения, обозначенной как +, для любых векторов  и скаляры
и скаляры  выполняется следующее равенство:
выполняется следующее равенство:

Обозначение нулевых элементов векторных пространств V и W как  и
и  соответственно, следует, что
соответственно, следует, что  Пусть c = 0 и
Пусть c = 0 и  в уравнении однородности степени 1:
в уравнении однородности степени 1:

Иногда, V и W могут быть векторными пространствами над разными полями. Затем необходимо указать, какое из этих основных полей используется в определении «линейного». Если V и W - пространства над тем же полем K, что и выше, то мы говорим о K-линейных отображениях. Например, спряжение комплексных чисел является ℝ-линейным отображением ℂ → ℂ, но оно не является ℂ-линейным, где ℝ и ℂ - символы, представляющие наборы действительных чисел. и комплексные числа соответственно.
Линейное отображение V → K, где K рассматривается как одномерное векторное пространство над собой, называется линейным функционалом.
Эти утверждения обобщаются на любой левый модуль  над кольцом R без модификации, и любому правому модулю после обращения скалярного умножения.
над кольцом R без модификации, и любому правому модулю после обращения скалярного умножения.
Примеры
- Типичным примером, который дает линейным картам их имя, является функция f: ℝ → ℝ: x ↦ cx, график которой представляет собой линию, проходящую через начало координат.
- Подробнее как правило, любая гомотетия с центром в начале векторного пространства,
 где c - скаляр, - линейный оператор. В общем случае это не выполняется для модулей, где такое отображение может быть только полулинейным.
где c - скаляр, - линейный оператор. В общем случае это не выполняется для модулей, где такое отображение может быть только полулинейным. - Нулевое отображение x ↦ 0 между двумя левыми модулями (или двумя правыми модулями) над одним и тем же кольцом всегда линейно.
- карта идентичности в любом модуле является линейным оператором.
- Для действительных чисел карта x ↦ x не является линейной.
- Для действительных чисел, отображение x ↦ x + 1 не является линейным (но является аффинным преобразованием ; y = x + 1 является линейным уравнением, поскольку этот термин используется в аналитическом геометрия.)
- Если A - вещественная матрица m × n , то A определяет линейную карту от ℝ до ℝ, отправляя вектор-столбец x∈ ℝ в вектор-столбец A x ∈ ℝ. И наоборот, любая линейная карта между конечномерными векторными пространствами может быть представлена таким образом; см. следующий раздел.
- Если F: X → Y является изометрия между действительными нормированными пространствами такая, что F (0) = 0, тогда F - линейное отображение. Этот результат не обязательно верен для сложного нормированного пространства.
- D ifferentiation определяет линейное отображение пространства всех дифференцируемых функций в пространство всех функций. Он также определяет линейный оператор в пространстве всех гладких функций (линейный оператор - это линейный эндоморфизм, то есть линейное отображение, где домен и кодомен у него одно и то же). Пример:
 .
. - Определенный интеграл на некотором интервале I - это линейная карта из пространства всех действительных -значные интегрируемые функции от I до ℝ. Например,
![{\displaystyle \int _{a}^{b}{[{{c}_{1}}{{f}_{1}}(x)+{{c}_{2}}{{f}_{2}}(x)+\ldots +{{c}_{n}}{{f}_{n}}(x)]dx}={{c}_{1}}\int _{a}^{b}{{{f}_{1}}(x)dx}+{{c}_{2}}\int _{a}^{b}{{{f}_{2}}(x)dx}+\ldots +{{c}_{n}}\int _{a}^{b}{{{f}_{n}}(x)dx}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d846ba13d174621b87518bfb239d5bc78fc91a0) .
. - Неопределенный интеграл (или первообразное ) с фиксированной начальной точкой интегрирования определяет линейное отображение из пространства всех действительных интегрируемых функций на в пространство всех действительных дифференцируемых функций на. Без фиксированной отправной точки упражнение по теории групп покажет, что первообразная отображается в факторпространство дифференцируемых по отношению эквивалентности «отличаются на константу», что дает тождественный класс постоянных функций
 .
. - Если V и W - конечномерные векторные пространства над полем F, то функции, которые отправляют линейные отображения f: V → W в dim F Матрицы (W) × dim F (V) в способе, описанном в дальнейшем, сами по себе являются линейными отображениями (действительно, линейные изоморфизмы ).
- ожидаемое значение случайная величина (которая на самом деле является функцией и как таковой член векторного пространства) является линейной, так как для случайных величин X и Y мы имеем E [X + Y] = E [X] + E [ Y] и E [aX] = aE [X], но дисперсия случайной величины не является линейной.
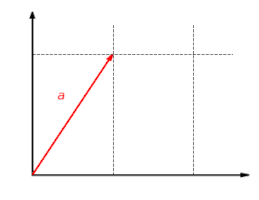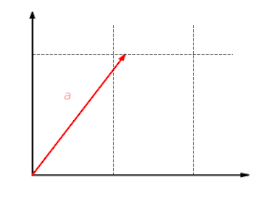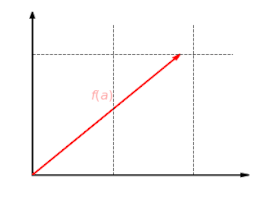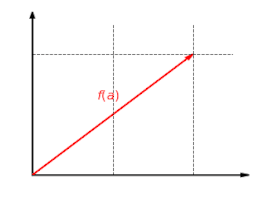
Функция  с
с  - линейная карта. Эта функция масштабирует компонент
- линейная карта. Эта функция масштабирует компонент  вектора на коэффициент
вектора на коэффициент  .
.
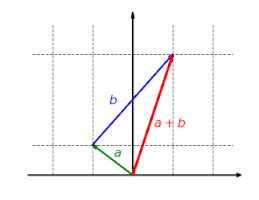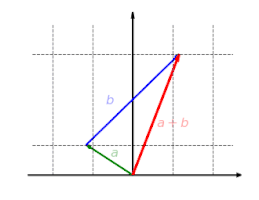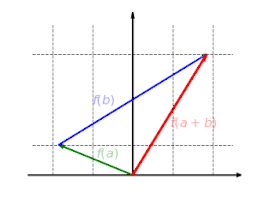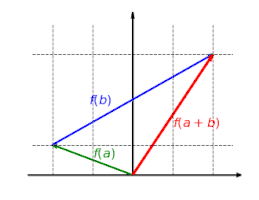
Функция  является аддитивным: не имеет значения, добавляются ли сначала векторы, а затем отображаются, или они отображаются и наконец добавлено:
является аддитивным: не имеет значения, добавляются ли сначала векторы, а затем отображаются, или они отображаются и наконец добавлено: 
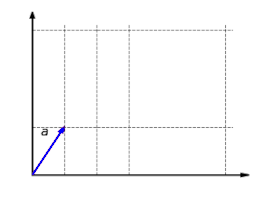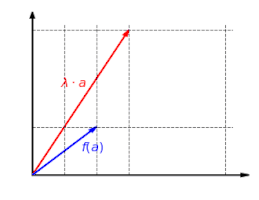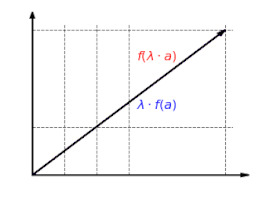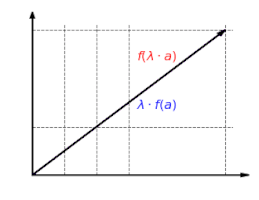
Функция  однородно: не имеет значения, масштабируется ли вектор сначала и затем отображается или сначала отображается и затем масштабируется:
однородно: не имеет значения, масштабируется ли вектор сначала и затем отображается или сначала отображается и затем масштабируется: 
Матрицы
Если V и W являются конечномерными векторными пространствами и для каждого векторного пространства определен базис, то каждая линейная карта из V в W может быть представлена матрицей . Это полезно, поскольку позволяет выполнять конкретные вычисления. Матрицы дают примеры линейных отображений: если A - вещественная матрица m × n, то f (x ) = A x описывает линейную карту R→ R(см. евклидово пробел ).
Пусть {v1,…, vn} будет базисом для V. Тогда каждый вектор v в V однозначно определяется коэффициентами c 1,…, C n в поле R:

Если f: V → W - линейная карта,

, что означает, что функция f полностью определяется векторами f (v1),…, f (vn). Теперь пусть {w1,…, wm} будет базисом для W. Тогда мы можем представить каждый вектор f (vj) как

Таким образом, функция f полностью определяется значениями a ij. Если мы поместим эти значения в матрицу M размером m × n, то мы сможем удобно использовать ее для вычисления векторного вывода f для любого вектора в V. Чтобы получить M, каждый столбец j матрицы M является вектором

соответствует f (vj), как определено выше. Чтобы определить его более четко, для некоторого столбца j, который соответствует отображению f (vj),

где M - матрица f. Другими словами, каждому столбцу j = 1,…, n соответствует вектор f (vj), координаты которого a 1j,…, a mj являются элементами столбца j. Одна линейная карта может быть представлена множеством матриц. Это происходит потому, что значения элементов матрицы зависят от выбранных оснований.
Матрицы линейного преобразования могут быть представлены визуально:
- Матрица для
 относительно
относительно  :
: 
- Матрица для
 относительно
относительно  :
: 
- Матрица перехода от
 к
к  :
: 
- Матрица перехода от
 до
до  :
: 
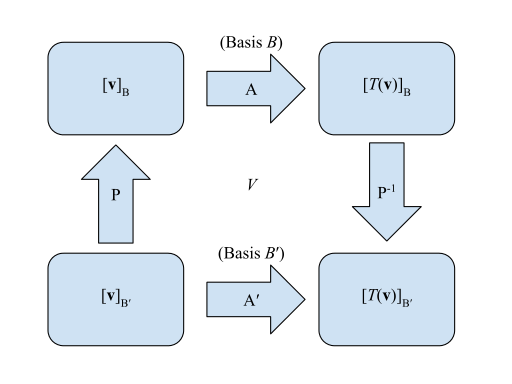
Таким образом, что начиная с нижний левый угол ![{\textstyle \left[{\vec {v}}\right]_{B'}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eacd96761ada855ad5b966859fee8f9655a7ddef) и ищем правый нижний угол
и ищем правый нижний угол ![{\textstyle \left[T\left({\vec {v}}\right)\right]_{B'}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/748437468b124fee67a0801c04390d4de1355e18) , можно умножить слева - то есть
, можно умножить слева - то есть ![{\textstyle A'\left[{\vec {v}}\right]_{B'}=\left[T\left({\vec {v}}\right)\right]_{B'}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b30a828a4a62a62e1d9698cb94b742b194447a86) . Эквивалентным методом будет «более длинный» метод, идущий по часовой стрелке из той же точки, так что
. Эквивалентным методом будет «более длинный» метод, идущий по часовой стрелке из той же точки, так что ![{\textstyle \left[{\vec {v}}\right]_{B'}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eacd96761ada855ad5b966859fee8f9655a7ddef) умножается слева на
умножается слева на  или
или ![{\textstyle P^{-1}AP\left[{\vec {v}}\right]_{B'}=\left[T\left({\vec {v}}\right)\right]_{B'}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5885c2daeb2a65ea8500890571c596b15b89f6ae) .
.
Примеры матриц линейного преобразования
В двух- мерном пространстве R описаны линейные карты на вещественные матрицы 2 × 2. Вот несколько примеров:
- поворот
- на 90 градусов против часовой стрелки:

- на угол θ против часовой стрелки:

- отражение
- вокруг оси x:

- вокруг оси y:

- вокруг оси с углом θ:

- Обратите внимание, что
 - это наклон линии, проходящей через начало координат
- это наклон линии, проходящей через начало координат
- с масштабированием на 2 всего направления:

- отображение горизонтального сдвига :

- отображение сжатия :

- проекция на ось y:

Формирование новых линейных карт из заданных
Состав линейных карт линейный : если f: V → W и g: W → Z линейны, то такова их композиция g ∘ f: V → Z. Отсюда следует, что класс всех векторные пространства над заданным полем K вместе с K-линейными отображениями в виде морфизмов образуют категорию.
обратная линейной карты, если она определена, снова линейная карта.
Если f 1 : V → W и f 2 : V → W линейны, то их поточечная сумма f <225 - тоже.>1 + f 2 (который определяется как (f 1 + f 2)(x) = (f 1(x) + f 2(x)).
Если f: V → W линейно и a является элементом основного поля K, то отображение af, определенное формулой (af) (x ) = a (f (x )), также является линейным.
Таким образом, множество L (V, W) линейных отображений из V в W само образует векторное пространство над K, иногда обозначаемое Hom (V, W). Кроме того, в случае, когда V = W, это векторное пространство (обозначенное End (V)) является ассоциативной алгеброй в рамках композиции отображений, поскольку композиция двух линейных отображений снова линейная карта, причем состав карт всегда ассоциативен. Более подробно этот случай обсуждается ниже.
Рассматривая снова конечномерный случай, если были выбраны базы, то композиция линейных карт соответствует умножению матриц, добавление линейных карт соответствует матрице сложение, а умножение линейных отображений на скаляры соответствует умножению матриц на скаляры.
Эндоморфизмы и автоморфизмы
Линейное преобразование f: V → V является эндоморфизмом V; набор всех таких эндоморфизмов End (V) вместе со сложением, композицией и скалярным умножением, как определено выше, образует ассоциативную алгебру с единичным элементом над полем K (и, в частности, кольцом ). Мультипликативным тождественным элементом этой алгебры является тождественное отображение id: V → V.
Эндоморфизм V, который также является изоморфизмом , называется автоморфизм группы V. Композиция двух автоморфизмов снова является автоморфизмом, и множество всех автоморфизмов V образует группу, группу автоморфизмов группы V, которая обозначается Aut (V) или GL (V). Поскольку автоморфизмы - это в точности те эндоморфизмы, которые обладают обратными по композиции, Aut (V) - это группа единиц в кольце End (V).
Если V имеет конечную размерность n, то End (V) изоморфна ассоциативной алгебре всех матриц размера n × n с элементами в K. Группа автоморфизмов матрицы V изоморфна общей линейной группе GL (n, K) всех обратимых матриц n × n с элементами в K.
Ядро, изображение и теорема ранга – недействительности
Если f: V → W является линейным, мы определяем ядро и изображение или диапазон f как

ker (f) является подпространством в V, а im (f) является подпространством W. следующая формула размерности известна как теорема ранга – недействительности :

Число dim (im (f)) также называется рангом функции f и записывается как rank (f) или иногда как ρ (f); число dim (ker (f)) называется нулевым значением f и записывается как null (f) или ν (f). Если V и W конечномерны, выбраны базы и f представлено матрицей A, то ранг и недействительность f равны rank и nullity матрица A соответственно.
Коядро
Более тонкий инвариант линейного преобразования  - это коядро, который определяется как
- это коядро, который определяется как

Это понятие, двойственное ядру: точно так же, как ядро является подпространство домена, со-ядро является частным пространством цели. Формально имеется точная последовательность

Их можно интерпретировать следующим образом: для решения линейного уравнения f (v ) = w,
- ядро - это пространство решений однородного уравнения f (v ) = 0, а его размерность - это количество степеней свободы в решении, если оно существует;
- ко-ядро - это пространство ограничений, которые должны быть выполнены, если уравнение должно иметь решение, а его размерность - это количество ограничений, которые должны быть выполнены для того, чтобы уравнение имело решение.
Размерность совместной -ядро и размер изображения (ранг) складываются в размер целевого пространства. Для конечных размеров это означает, что размерность фактор-пространства W / f (V) - это размерность целевого пространства минус размерность изображения.
В качестве простого примера рассмотрим карту f: R→ R, заданную формулой f (x, y) = (0, y). Тогда для того, чтобы уравнение f (x, y) = (a, b) имело решение, мы должны иметь a = 0 (одно ограничение), и в этом случае пространство решений равно (x, b) или, что эквивалентно, ( 0, b) + (x, 0), (одна степень свободы). Ядро может быть выражено как подпространство (x, 0) < V: the value of x is the freedom in a solution – while the cokernel may be expressed via the map W → R,  с заданным вектором (a, b), значение a является препятствием для решения.
с заданным вектором (a, b), значение a является препятствием для решения.
Пример, иллюстрирующий случай бесконечной размерности, дает карта f: R→ R,  с b 1 = 0 и b n + 1 = a n для n>0. Его образ состоит из всех последовательностей с первым элементом 0, поэтому его коядро состоит из классов последовательностей с одинаковым первым элементом. Таким образом, в то время как его ядро имеет размерность 0 (оно отображает только нулевую последовательность в нулевую последовательность), его ко-ядро имеет размерность 1. Поскольку область определения и целевое пространство одинаковы, ранг и размерность ядра складываются. к той же сумме, что и ранг и размер со-ядра (
с b 1 = 0 и b n + 1 = a n для n>0. Его образ состоит из всех последовательностей с первым элементом 0, поэтому его коядро состоит из классов последовательностей с одинаковым первым элементом. Таким образом, в то время как его ядро имеет размерность 0 (оно отображает только нулевую последовательность в нулевую последовательность), его ко-ядро имеет размерность 1. Поскольку область определения и целевое пространство одинаковы, ранг и размерность ядра складываются. к той же сумме, что и ранг и размер со-ядра ( ), но в бесконечномерном случае нельзя сделать вывод, что ядро и ко-ядро эндоморфизма имеют одинаковую размерность (0 1). Обратная ситуация имеет место для карты h: R→ R,
), но в бесконечномерном случае нельзя сделать вывод, что ядро и ко-ядро эндоморфизма имеют одинаковую размерность (0 1). Обратная ситуация имеет место для карты h: R→ R,  с c n = a n + 1. Его изображение - это все целевое пространство, и, следовательно, его со-ядро имеет размерность 0, но поскольку он отображает все последовательности, в которых только первый элемент не равен нулю, в нулевую последовательность, его ядро имеет размерность 1.
с c n = a n + 1. Его изображение - это все целевое пространство, и, следовательно, его со-ядро имеет размерность 0, но поскольку он отображает все последовательности, в которых только первый элемент не равен нулю, в нулевую последовательность, его ядро имеет размерность 1.
Индекс
Для линейного оператора с конечномерным ядром и ко-ядром индекс можно определить как:

а именно степени свободы минус количество ограничений.
Для преобразования между конечномерными векторными пространствами это просто разница dim (V) - dim (W) по рангу – нулю. Это дает представление о том, сколько решений или сколько ограничений у вас есть: если отображение из большего пространства в меньшее, карта может быть включена и, следовательно, будет иметь степени свободы даже без ограничений. И наоборот, если отображение из меньшего пространства в большее, карта не может быть на, и, таким образом, у вас будут ограничения даже без степеней свободы.
Индекс оператора - это в точности эйлерова характеристика 2-членного комплекса 0 → V → W → 0. В теории операторов индекс Операторы Фредгольма являются объектом исследования, основным результатом которого является теорема Атьи – Зингера об индексе.
Алгебраическая классификация линейных преобразований
Никакая классификация линейных отображений не может быть исчерпывающей. В следующем неполном списке перечислены некоторые важные классификации, которые не требуют какой-либо дополнительной структуры в векторном пространстве.
Пусть V и W обозначают векторные пространства над полем F и пусть T: V → W - линейное отображение.
Определение : T называется инъективным или мономорфизмом, если выполняется любое из следующих эквивалентных условий:
- T однозначно -one в качестве карты устанавливает.
- ker T = {0 V}
- dim (kerT) = 0
- T is monic или с возможностью отмены слева, другими словами, для любого векторного пространства U и любой пары линейных отображений R: U → V и S: U → V уравнение TR = TS влечет R = S.
- T слева -обратимое, то есть существует линейное отображение S: W → V такое, что ST является тождественным отображением на V.
Определение : T называется сюръективный или эпиморфизм, если выполняется любое из следующих эквивалентных условий:
- T является на как карта множеств.
- coker T = {0 W}
- T является эпическим или сокращаемым справа, то есть для любого векторного пространства U и любой пары линейных отображений R: W → U и S: W → U уравнение RT = ST подразумевает R = S.
- T является обратимым вправо, то есть существует линейное отображение S : W → V такое, что TS является тождественным отображением на W.
Определение : T называется изоморфизмом , если он является как левым, так и правым. обратимый. Это эквивалентно тому, что T является одновременно взаимно однозначным и на (биекция множеств) или также тому, что T является одновременно эпическим и моническим, и поэтому является биморфизмом.
Если T: V → V - эндоморфизм, то:
- Если для некоторого положительного целого числа n n-я итерация T, T, тождественно равна нулю, то T называется нильпотентным.
- Если T = T, то T называется идемпотентным
- Если T = kI, где k - некоторый скаляр, то T называется масштабным преобразованием или отображением скалярного умножения; см. скалярная матрица.
Изменение базиса
Учитывая линейную карту, которая является эндоморфизмом, матрица которого равна A, в базисе B пространства она преобразует векторные координаты [u ] как [v] = A [u]. Поскольку векторы изменяются вместе с обратным B (векторы контравариантны ), его обратное преобразование равно [v] = B [v '].
Подставляем это в первое выражение
![{\displaystyle B\left[v'\right]=AB\left[u'\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2855717373418c2c2134151c0d0f4d5957292f8)
, следовательно,
![{\displaystyle \left[v'\right]=B^{-1}AB\left[u'\right]=A'\left[u'\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65eb8aa4babed0054fcf025303d23fd58309bf7e)
Следовательно, матрица в новом базисом является A ′ = BAB, где B - матрица данного базиса.
Следовательно, линейные карты называются 1-co-1-contra- вариантами объектами или типом (1, 1) тензорами.
Continuity
Линейное преобразование между топологическими векторными пространствами, например, нормированными пространствами, может быть непрерывным. Если его домен и код домен совпадают, тогда это будет непрерывный линейный оператор . Линейный оператор на линейном нормированном пространстве непрерывен тогда и только тогда, когда он ограничен, например, когда область конечномерна. Бесконечномерная область может иметь разрывные линейные операторы.
Примером неограниченного, а следовательно, прерывного линейного преобразования является дифференцирование на пространстве гладких функций, снабженное нормой супремума (функция с малыми значениями может иметь производную с большими значениями, а производная 0 равна 0). В конкретном примере sin (nx) / n сходится к 0, но его производная cos (nx) - нет, поэтому дифференцирование не является непрерывным в 0 (и, согласно вариации этого аргумента, оно не является непрерывным нигде).
Приложения
Специальное приложение линейных карт предназначено для геометрических преобразований, таких как те, которые выполняются в компьютерной графике, где перемещение, вращение и масштабирование 2D или 3D объектов выполняется с использованием матрицы преобразования . Линейные отображения также используются как механизм для описания изменений: например, в исчислении соответствуют производным; или в теории относительности, используемый как устройство для отслеживания локальных преобразований систем отсчета.
Другое применение этих преобразований - оптимизация компилятора кода вложенного цикла и методы распараллеливания компилятора.
См. Также
Примечания
Библиография
- Бронштейн И.Н. Семендяев, К. А. (2004). Справочник по математике (4-е изд.). Нью-Йорк: Springer-Verlag. ISBN 3-540-43491-7.
- Халмос, Пол Р. (1974). Конечномерные векторные пространства. Нью-Йорк: Спрингер-Верлаг. ISBN 0-387-90093-4.
- Хорн, Роджер А.; Джонсон, Чарльз Р. (2013). Матричный анализ (второе изд.). Издательство Кембриджского университета. ISBN 978-0-521-83940-2.
- Лэнг, Серж (1987), Линейная алгебра (третье изд.), Нью-Йорк: Springer-Verlag, ISBN 0-387-96412-6
- Рудин, Уолтер (1973). Функциональный анализ. Международная серия по чистой и прикладной математике. 25 (Первое изд.). Нью-Йорк, штат Нью-Йорк: McGraw-Hill Science / Engineering / Math. ISBN 9780070542259.
- Рудин, Вальтер (1976). Принципы математического анализа. Вальтер Рудин Студенческая серия по высшей математике (3-е изд.). Нью-Йорк: Макгроу – Хилл. ISBN 978-0-07-054235-8.
- Рудин, Уолтер (1991). Функциональный анализ. Международная серия по чистой и прикладной математике. 8 (Второе изд.). Нью-Йорк, штат Нью-Йорк: McGraw-Hill Science / Engineering / Math. ISBN 978-0-07-054236-5. OCLC 21163277.
- Шефер, Гельмут Х. ; (1999). Топологические векторные пространства. GTM. 8(Второе изд.). Нью-Йорк, штат Нью-Йорк: Springer New York Выходные данные Springer. ISBN 978-1-4612-7155-0. OCLC 840278135.
- Шварц, Чарльз (1992). Введение в функциональный анализ. Нью-Йорк: М. Деккер. ISBN 978-0-8247-8643-4. OCLC 24909067.
- Вилански, Альберт (2013). Современные методы в топологических векторных пространствах. Минеола, Нью-Йорк: Dover Publications, Inc. ISBN 978-0-486-49353-4. OCLC 849801114.












 где c - скаляр, - линейный оператор. В общем случае это не выполняется для модулей, где такое отображение может быть только полулинейным.
где c - скаляр, - линейный оператор. В общем случае это не выполняется для модулей, где такое отображение может быть только полулинейным. .
.![{\displaystyle \int _{a}^{b}{[{{c}_{1}}{{f}_{1}}(x)+{{c}_{2}}{{f}_{2}}(x)+\ldots +{{c}_{n}}{{f}_{n}}(x)]dx}={{c}_{1}}\int _{a}^{b}{{{f}_{1}}(x)dx}+{{c}_{2}}\int _{a}^{b}{{{f}_{2}}(x)dx}+\ldots +{{c}_{n}}\int _{a}^{b}{{{f}_{n}}(x)dx}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d846ba13d174621b87518bfb239d5bc78fc91a0) .
. .
.













 относительно
относительно  :
: 
 относительно
относительно  :
: 
 к
к  :
: 
 до
до  :
: 

![{\textstyle \left[{\vec {v}}\right]_{B'}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eacd96761ada855ad5b966859fee8f9655a7ddef)
![{\textstyle \left[T\left({\vec {v}}\right)\right]_{B'}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/748437468b124fee67a0801c04390d4de1355e18)
![{\textstyle A'\left[{\vec {v}}\right]_{B'}=\left[T\left({\vec {v}}\right)\right]_{B'}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b30a828a4a62a62e1d9698cb94b742b194447a86)
![{\textstyle \left[{\vec {v}}\right]_{B'}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eacd96761ada855ad5b966859fee8f9655a7ddef)

![{\textstyle P^{-1}AP\left[{\vec {v}}\right]_{B'}=\left[T\left({\vec {v}}\right)\right]_{B'}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5885c2daeb2a65ea8500890571c596b15b89f6ae)





 - это наклон линии, проходящей через начало координат
- это наклон линии, проходящей через начало координат













![{\displaystyle B\left[v'\right]=AB\left[u'\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2855717373418c2c2134151c0d0f4d5957292f8)
![{\displaystyle \left[v'\right]=B^{-1}AB\left[u'\right]=A'\left[u'\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65eb8aa4babed0054fcf025303d23fd58309bf7e)