Банахово пространство

Полное нормированное векторное пространство

В математике, более конкретно в функциональный анализ, банахово пространство (произносится ) является полным нормированным векторным пространством. Таким образом, банахово пространство - это векторное пространство с метрикой , которое позволяет вычислять длину вектора и расстояние между векторами, и является полным в том смысле, что последовательность Коши векторов всегда сходится к четко определенному пределу , который находится в пределах пространства.

Пространства Банаха названы в честь польского математика Стефана Банаха, который представил это понятие и систематически изучал его в 1920–1922 годах вместе с Хансом Ханом и Эдуардом. Хелли. Морис Рене Фреше был первым, кто использовал термин «пространство Банаха», а Банах, в свою очередь, ввел термин «пространство Фреше ». Банаховы пространства первоначально выросли из исследования функциональных пространств, проведенного Гильбертом, Фреше и Риссом в начале века. Банаховы пространства играют центральную роль в функциональном анализе. В других областях анализа исследуемые пространства часто являются банаховыми.

• 1 Определение
  • 1.1 Полнота
  • 1.2 Завершение
• 2 Общая теория
  • 2.1 Линейные операторы, изоморфизмы
  • 2.2 Основные понятия
  • 2.3 Классические пространства
  • 2.4 Банах алгебры
    • 2.4.1 Примеры
  • 2.5 Двойное пространство
    • 2.5.1 Слабые топологии
    • 2.5.2 Примеры двойственных пространств
    • 2.5.3 Двустороннее
  • 2.6 Теоремы Банаха
  • 2.7 Рефлексивность
  • 2.8 Слабые сходимости последовательностей
    • 2.8.1 Результаты с использованием базиса
    • 2.8.2 Последовательности, слабые и слабые * компактность
• 3 базиса Шаудера
• 4 Тензорное произведение
  • 4.1 Тензорное произведение и свойство аппроксимации
• 5 Некоторые результаты классификации
  • 5.1 Характеризация гильбертова пространства среди банаховых пространств
  • 5.2 Метрическая классификация
  • 5.3 Топологическая классификация
  • 5.4 Пространства непрерывных функций
• 6 Примеры
• 7 Производные
• 8 Обобщения
• 9 См. Также
• 10 Примечания
• 11 Ссылки
• 12 Библиография
• 13 Внешние ссылки

A Банахово пространство - это полная норма ed пробел (X, || ⋅ ||). Нормированное пространство - это пара (X, || ⋅ ||), состоящая из векторного пространства X над скалярным полем K вместе с выделенной нормой || ⋅ ||. Как и все нормы, эта норма индуцирует инвариант перевода функцию расстояния, называемую канонической или (нормой ) индуцированной метрикой, определяемый

d (x, y): = || y - x ||

для всех векторов x, y ∈ X. Это превращает X в метрическое пространство (X, г). По определению, нормированное пространство (X, || ⋅ ||) является банаховым пространством тогда и только тогда, когда (X, d) является полным метрическим пространством, или, иначе говоря, тогда и только тогда, когда каноническое метрика d - это полная метрика. Каноническая метрика d является полной тогда и только тогда, когда для каждой последовательности d- Коши x•= (x n). n = 1 в (X, d) существует элемент x ∈ X такой, что

$lim\; n\; \to \; \infty \; \Vert \; xn\; -\; x\; \Vert \; =\; 0\; \{\backslash \; displaystyle\; \backslash \; lim\; \_\; \{n\; \backslash \; to\; \backslash \; infty\}\; \backslash \; left\; \backslash \; |\; x\_\; \{n\}\; -x\; \backslash \; right\; \backslash \; |\; =\; 0\}$

где обратите внимание, что поскольку || x n - x || = d (x n, x), эта сходимость может быть эквивалентно выражена как: $lim\; n\; \to \; \infty \; xn\; =\; x\; \{\backslash \; displaystyle\; \backslash \; lim\; \_\; \{n\; \backslash \; to\; \backslash \; infty\}\; x\_\; \{n\}\; =\; x\}$in (X, d). Последовательность x • равна d-Cauchy или Коши в (X, d) тогда и только тогда, когда для каждого действительного r>0 существует некоторый индекс N такой, что

d (x n, x m) = || x n - x m || < r

всякий раз, когда m и n больше N. Для любого нормированного пространства (X, || ⋅ ||), мы говорим, что его норма является полной тогда и только тогда, когда (X, || ⋅ ||) является банаховым пространством.

L-полускалярное произведение

Для любого нормированного space (X, || ⋅ ||), существует L-полувинарное произведение ("L" для Günter Lumer ) ⟨⋅, ⋅⟩ на X такое, что || х || = √⟨x, x⟩ для всех x ∈ X; в общем, может быть бесконечно много L-полускалярных произведений, удовлетворяющих этому условию. L-полускалярные произведения являются обобщением скалярных произведений, которые фундаментально отличает гильбертовы пространства от всех других банаховых пространств. Это показывает, что все нормированные пространства (и, следовательно, все банаховы пространства) можно рассматривать как обобщения (пред) гильбертовых пространств.

Топология

Каноническая метрика d нормированного пространства (X, || ⋅ ||) индуцирует обычную метрическую топологию τdна X, где эта топология, которая является называемая канонической или индуцированной нормой топологией, превращает (X, τ d) в Hausdorff метризуемую топологическое пространство. Автоматически предполагается, что каждое нормированное пространство несет эту топологию, если не указано иное. При такой топологии каждое банахово пространство является бэровским пространством, хотя есть нормированные пространства, которые являются бэровскими, но не банаховыми. Эта индуцированная нормой топология всегда превращает норму в непрерывное отображение || ⋅ || : (X, τ d) → ℝ.

Эта индуцированная нормой топология также превращает (X, τ d) в то, что известно как топологическое векторное пространство (TVS), которое по определению является векторное пространство, наделенное топологией, делающей непрерывными операции сложения и скалярного умножения. Подчеркивается, что TVS (X, τ d) не связан с какой-либо конкретной нормой или метрикой; это всего лишь векторное пространство вместе с определенной топологией.

Полнота

Полные нормы и эквивалентные нормы

Две нормы в векторном пространстве называются эквивалентными тогда и только тогда, когда они порождают одну и ту же топологию. Если p и q - две эквивалентные нормы на векторном пространстве X, то (X, p) является банаховым пространством тогда и только тогда, когда (X, q) является банаховым пространством. В этой сноске показан пример непрерывной нормы в банаховом пространстве, которая не эквивалентна данной норме этого банахова пространства. Все нормы в конечномерном векторном пространстве эквивалентны, и каждое конечномерное нормированное пространство является банаховым пространством.

Полные нормы и полные метрики

Предположим, что (X, || ⋅ ||) - нормированное пространство и что τ - нормальная топология, индуцированная на X. Предположим, что D - любая метрика на X такая, что топология, индуцируемая D на X, равна τ. Если D инвариант относительно сдвига, то (X, || ⋅ ||) является банаховым пространством тогда и только тогда, когда (X, D) является полным метрическим пространством. Если D не является трансляционно-инвариантным, тогда (X, || ⋅ ||) может быть банаховым пространством, но (X, D) не будет полным метрическим пространством (см. Эту сноску в качестве примера). Напротив, теорема Кли, которая также применяется ко всем метризуемым топологическим векторным пространствам, подразумевает, что если существует какая-либо полная метрика D на X, которая индуцирует топологию нормы на X, то (X, || ⋅ ||) - банахово пространство.

Метрика D на векторном пространстве X индуцирована нормой на X тогда и только тогда, когда D инвариантен относительно сдвига и абсолютно однороден, что означает, что D (sx, sy) = | с | D (x, y) для всех скаляров s и всех x, y ∈ X, и в этом случае функция || x || : = D (x, 0) определяет норму на X и каноническую метрику, индуцированную || ⋅ || равно D.

Полные нормы и полные топологические векторные пространства

Существует еще одно понятие полноты, помимо метрической полноты, и это понятие полного топологического векторного пространства (TVS) или TVS- полнота. Это понятие зависит только от векторного вычитания и топологии τ, которой наделено векторное пространство, поэтому, в частности, это понятие полноты TVS не зависит от того, какая норма индуцировала топологию τ (и даже применяется к TVS, которые даже не являются метризуемыми). Каждое банахово пространство - это полная ТВС. Более того, нормированное пространство является банаховым пространством (т.е. его каноническая метрика полна) тогда и только тогда, когда оно полно как топологическое векторное пространство. Кроме того, если (X, τ) является топологическим векторным пространством, топология которого индуцирована некоторой нормой, то (X, τ) является полным топологическим векторным пространством тогда и только тогда, когда X можно присвоить>норма || ⋅ || который индуцирует на X топологию τ, а также превращает (X, || ⋅ ||) в банахово пространство. Если (X, τ) является метризуемым топологическим векторным пространством (где отметим, что любая индуцированная нормой топология метризуема), то (X, τ) является полным TVS тогда и только тогда, когда оно является последовательно полным TVS, что означает, что достаточно проверить, что каждая последовательность Коши в (X, τ) сходится в (X, τ) к некоторой точке X.

Характеризация в терминах серий

Структура векторного пространства позволяет связать поведение последовательностей Коши сходится с последовательностями векторов. Нормированное пространство X является банаховым тогда и только тогда, когда каждый абсолютно сходящийся ряд в X сходится в X,

.

Пополнения

Каждые нормированное пространство может быть изометрически вложено в плотное векторное подпространство некоторого банахова пространства, причем это банахово пространство называется пополнением нормированного пространства. Это пополнение единственно с точностью до изометрического изоморфизма.

Точнее, для любого нормированного пространства X существуют банахово пространство Y и отображение T: X → Y такие, что T является изометрическим отображением и T (X) плотно в Y. Если Z - другое банахово пространство такое, что существует изометрический изоморфизм X на плотное подмножество Z, то Z изометрически изоморфно Y. Это банахово пространство Y является пополнением нормированного пространства X. Базовое метрическое пространство для Y такое же, как метрическое завершение X, с операциями векторного пространства, расширенными от X до Y. Завершение X часто обозначается $X\; ^\; \{\backslash \; displaystyle\; \{\backslash \; widehat\; \{X\}\}\}$.

.

Линейные операторы, изоморфизмы

Если X и Y являются нормированными пространствами над одним и тем же основным полем K, множество всех непрерывных K-линейных отображений T: X → Y обозначается через B (X, Y). В бесконечномерных пространствах не все линейные отображения непрерывны. Линейное отображение нормированного пространства X в другое нормированное пространство непрерывно тогда и только тогда, когда оно ограничено на замкнутом единичном шаре пространства X. Таким образом, векторное пространство B (X, Y) можно задать операторную норму

$\Vert \; T\; \Vert \; =\; sup\; \{\Vert \; T\; x\; \Vert \; Y\; \mid \; x\; \in \; X,\; \Vert \; x\; \Vert \; X\; \le \; 1\}.\; \{\backslash \; Displaystyle\; \backslash \; |\; T\; \backslash \; |\; =\; \backslash \; sup\; \backslash \; left\; \backslash \; \{\backslash \; |\; Tx\; \backslash \; |\; \_\; \{Y\}\; \backslash \; mid\; x\; \backslash \; in\; X,\; \backslash \; \backslash \; |\; x\; \backslash \; |\; \_\; \{X\}\; \backslash \; leq\; 1\; \backslash \; right\; \backslash \}.\}$

Для Y - банахова пространства, пространство B (X, Y) - банахово пространство относительно этой нормы.

Если X - банахово пространство, пространство B (X) = B (X, X) образует унитальную банахову алгебру ; операция умножения задается композицией линейных отображений.

Если X и Y - нормированные пространства, они являются изоморфными нормированными пространствами, если существует линейная биекция T: X → Y такая, что T и его обратный T непрерывны. Если одно из двух пробелов X или Y является полным (или рефлексивным, отделимым и т. Д.), То другое пространство тоже. Два нормированных пространства X и Y изометрически изоморфны, если, кроме того, T является изометрией, т.е. || T (x) || = || х || для каждого x в X. Расстояние Банаха – Мазура d (X, Y) между двумя изоморфными, но не изометрическими пространствами X и Y дает меру того, насколько два пространства X и Y различаются.

Основные понятия

Декартово произведение X × Y двух нормированных пространств канонически не снабжено нормой. Однако обычно используются несколько эквивалентных норм, например

$\Vert \; (x,\; y)\; \Vert \; 1\; =\; \Vert \; x\; \Vert \; +\; \Vert \; y\; \Vert ,\; \Vert \; (x,\; y)\; \Vert \; \infty \; =\; max\; (\Vert \; x\; \Vert ,\; \Vert \; y\; \Vert )\; \{\backslash \; displaystyle\; \backslash \; |\; (x,\; y)\; \backslash \; |\; \_\; \{1\}\; =\; \backslash \; |\; x\; \backslash \; |\; +\; \backslash \; |\; y\; \backslash \; |,\; \backslash \; qquad\; \backslash \; |\; (x,\; y)\; \backslash \; |\; \_\; \{\backslash \; infty\}\; =\; \backslash \; max\; (\backslash \; |\; x\; \backslash \; |,\; \backslash \; |\; y\; \backslash \; |)\}$

и порождают изоморфные нормированные пространства. В этом смысле произведение X × Y (или прямая сумма X ⊕ Y) является полным тогда и только тогда, когда два множителя полны.

Если M является замкнутым линейным подпространством нормированного пространства X, существует естественная норма на фактор-пространстве X / M,

$\Vert \; x\; +\; M\; \Vert \; =\; inf\; m\; \in \; M\; \Vert \; x\; +\; m\; \Vert .\; \{\backslash \; displaystyle\; \backslash \; |\; x\; +\; M\; \backslash \; |\; =\; \backslash \; inf\; \backslash \; limits\; \_\; \{m\; \backslash \; in\; M\}\; \backslash \; |\; x\; +\; m\; \backslash \; |.\}$

Частное X / M является банаховым пространством, когда X является полным. Факторное отображение от X на X / M, отправляющее x в X в его класс x + M, является линейным, на и имеет норму 1, за исключением случаев, когда M = X, и в этом случае частным является нуль. Космос.

Замкнутое линейное подпространство M в X называется дополняемым подпространством X, если M является диапазоном ограниченной линейной проекции P из X на M. В этом случае пространство X изоморфно прямой сумме M и Ker (P), ядру проекции P.

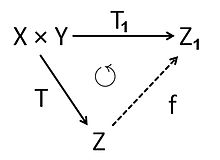
Предположим, что X и Y - банаховы пространства и что T ∈ B (X, Y). Существует каноническая факторизация числа T как

$T\; =\; T\; 1\; \circ \; \pi ,\; T:\; X\; ⟶\; \pi \; X\; /\; Ker\; \; (T)\; ⟶\; T\; 1\; Y\; \{\backslash \; displaystyle\; T\; =\; T\_\; \{1\}\; \backslash \; circ\; \backslash \; pi,\; \backslash \; \backslash \; \backslash \; T:\; X\; \backslash \; \{\backslash \; overset\; \{\backslash \; pi\}\; \{\backslash \; longrightarrow\}\}\; \backslash \; X\; /\; \backslash \; operatorname\; \{Ker\}\; (T)\; \backslash \; \{\backslash \; overset\; \{T\_\; \{1\}\}\; \{\backslash \; longrightarrow\}\}\; \backslash \; Y\}$

, где первое отображение π является фактор-картой, а второе отображение T 1 отправляет каждый класс x + Ker (T) в частном к изображению T (x) в Y. Это хорошо определен, потому что все элементы в одном классе имеют одно и то же изображение. Отображение T 1 является линейной биекцией из X / Ker (T) на область значений T (X), обратная к которой не должна быть ограничена.

Классические пространства

Основные примеры банаховых пространств включают: L-пространства и их особые случаи, пространства последовательностей ℓ, которые состоят из скалярных последовательностей проиндексировано N ; среди них пространство ℓ абсолютно суммируемых последовательностей и пространство ℓ квадратично суммируемых последовательностей; пространство c 0 последовательностей, стремящихся к нулю, и пространство ℓ ограниченных последовательностей; пространство C (K) непрерывных скалярных функций на компактном хаусдорфовом пространстве K, снабженное максимальной нормой,

$\Vert \; f\; \Vert \; C\; (K)\; =\; max\; \{|\; f\; (x)\; |\; :\; x\; \in \; K\},\; f\; \in \; C\; (K).\; \{\backslash \; Displaystyle\; \backslash \; |\; е\; \backslash \; |\; \_\; \{C\; (K)\}\; =\; \backslash \; max\; \backslash \; \{|\; f\; (x)\; |:\; x\; \backslash \; in\; K\; \backslash \},\; \backslash \; quad\; f\; \backslash \; in\; C\; (K).\}$

Согласно теорема Банаха – Мазура, каждое банахово пространство изометрически изоморфно подпространству некоторого C (K). Для любого сепарабельного банахова пространства X существует замкнутое подпространство M в такое, что X ≅ ℓ / M.

Любое гильбертово пространство служит примером банахова пространства. Гильбертово пространство H на K= R, Cявляется полным для нормы вида

$\Vert \; x\; \Vert \; H\; =\; ⟨x,\; x⟩,\; \{\backslash \; displaystyle\; \backslash \; |\; x\; \backslash \; |\; \_\; \{H\}\; =\; \{\backslash \; sqrt\; \{\backslash \; langle\; x,\; x\; \backslash \; rangle\}\},\}$

где

$⟨\cdot ,\; \cdot ⟩:\; H\; \times \; H\; \to \; K\; \{\backslash \; displaystyle\; \backslash \; langle\; \backslash \; cdot,\; \backslash \; cdot\; \backslash \; rangle:\; H\; \backslash \; times\; H\; \backslash \; to\; \backslash \; mathbf\; \{K\}\; \}$

- это внутренний продукт, линейный по своему первому аргументу, который удовлетворяет следующему:

$\forall \; x,\; y\; \in \; H:\; ⟨y,\; x⟩\; =\; ⟨x,\; y⟩\; ¯,\; \forall \; x\; \in \; H:\; ⟨Икс,\; Икс⟩\; \ge \; 0,\; ⟨Икс,\; Икс⟩\; знак\; равно\; 0\; \iff \; Икс\; =\; 0.\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; forall\; x,\; y\; \backslash \; в\; H:\; \backslash \; quad\; \backslash \; langle\; y,\; x\; \backslash \; rangle\; =\; \{\backslash \; overline\; \{\backslash \; langle\; x,\; y\; \backslash \; rangle\}\},\; \backslash \backslash \backslash \; forall\; x\; \backslash \; in\; H:\; \backslash \; quad\; \backslash \; langle\; x,\; x\; \backslash \; rangle\; \backslash \; geq\; 0,\; \backslash \backslash \backslash \; langle\; x,\; x\; \backslash \; rangle\; =\; 0\; \backslash \; Leftrightarrow\; x\; =\; 0.\; \backslash \; End\; \{align\}\}\}$

Например, пространство L является гильбертовым пространством.

пространства Харди, пространства Соболева являются примерами банаховых пространств, которые связаны с пространствами L и имеют дополнительную структуру. Они важны в различных областях анализа, среди которых Гармонический анализ и Уравнения с частными производными.

Банахова алгебра

A Банахова алгебра - это банахово пространство A над K= Rили C вместе со структурой алгебры над K, такое, что отображение произведения A × A ∋ (a, b) ↦ ab ∈ A непрерывно. Эквивалентную норму на A можно найти так, что || ab || ≤ || а || || b || для всех a, b ∈ A.

Примеры

• Банахово пространство C (K) с поточечным произведением является банаховой алгеброй.
• Дисковая алгебра A(D) состоит из функций , голоморфных в открытом единичном диске D⊂ Cи непрерывных на его замыкании : D. Дисковая алгебра A (D ), снабженная максимальной нормой на D, является замкнутой подалгеброй в C (D).
• алгебра Винера A(T) является алгеброй функций на единичной окружности T с абсолютно сходящимся рядом Фурье. С помощью карты, связывающей функцию на T с последовательностью ее коэффициентов Фурье, эта алгебра изоморфна банаховой алгебре ℓ (Z ), где произведение представляет собой свертку последовательностей.
• Для любого банахова пространства X пространство B (X) ограниченных линейных операторов на X с композицией отображений в качестве произведения является банаховой алгеброй.
• A C * - алгебра является комплексной банаховой алгеброй A с антилинейной инволюцией a ↦ a такой, что || aa || = || а ||. Пространство B (H) линейных ограниченных операторов в гильбертовом пространстве H является фундаментальным примером C * -алгебры. Теорема Гельфанда – Наймарка утверждает, что любая C * -алгебра изометрически изоморфна C * -подалгебре некоторой B (H). Пространство C (K) комплексных непрерывных функций на компактном хаусдорфовом пространстве K является примером коммутативной C * -алгебры, где инволюция сопоставляет каждой функции f ее комплексно сопряженное f.

Двойственное пространство

Если X - нормированное пространство и K базовое поле (либо действительное, либо комплексное числа), непрерывное двойственное пространство - это пространство непрерывных линейных отображений из X в K или непрерывных линейных функционалов . Обозначение для непрерывного двойственного в этой статье: X ′ = B (X, K ). Поскольку K является банаховым пространством (с использованием абсолютного значения в качестве нормы), двойственное X ′ является банаховым пространством для любого нормированного пространства X.

Основное Инструмент для доказательства существования непрерывных линейных функционалов - это теорема Хана – Банаха.

теорема Хана – Банаха. Пусть X - векторное пространство над полем K= R, C. Пусть дополнительно

• Y ⊆ X будет линейным подпространством,
• p: X → R будет сублинейной функцией и
• f : Y → K - линейный функционал, так что Re (f (y)) ≤ p (y) для всех y в Y.

Тогда существует линейный функционал F: X → K, так что

$F\; |\; Y\; =\; f\; и\; \forall \; x\; \in \; X,\; Re\; \; (F\; (x))\; \le \; p\; (x).\; \{\backslash \; Displaystyle\; F\; |\; \_\; \{Y\}\; =\; е,\; \backslash \; quad\; \{\backslash \; text\; \{и\}\}\; \backslash \; quad\; \backslash \; forall\; x\; \backslash \; in\; X,\; \backslash \; \backslash \; \backslash \; operatorname\; \{Re\}\; (F\; (x))\; \backslash \; leq\; p\; (x).\; \}$

В частности, каждый непрерывный линейный функционал на подпространстве нормированного пространства может быть непрерывно расширен на все пространство без увеличения нормы функционала. Важным частным случаем является следующий: для каждого вектора x в нормированном пространстве X существует непрерывный линейный функционал f на X такой, что

$f\; (x)\; =\; \Vert \; x\; \Vert \; X,\; \Vert \; f\; \Vert \; X\; \prime \; \le \; 1.\; \{\backslash \; displaystyle\; f\; (x)\; =\; \backslash \; |\; x\; \backslash \; |\; \_\; \{X\},\; \backslash \; quad\; \backslash \; |\; f\; \backslash \; |\; \_\; \{X\; \text{'}\}\; \backslash \; leq\; 1.\}$

Когда x не равно 0 вектор функционал f должен иметь норму один и называется нормирующим функционалом для x.

Теорема Хана – Банаха об отделимости утверждает, что два непересекающихся непустых выпуклых множества в реальном банаховом пространстве, одно из которых открыто, могут быть разделены замкнутым affine гиперплоскость. Открытое выпуклое множество лежит строго по одну сторону от гиперплоскости, второе выпуклое множество лежит с другой стороны, но может касаться гиперплоскости.

Подмножество S в банаховом пространстве X всего если линейная оболочка S является плотной в X. Подмножество S является тотальным в X тогда и только тогда, когда единственным непрерывным линейным функционалом, который исчезает на S, является 0 функционал: эта эквивалентность следует из теоремы Хана – Банаха.

Если X - прямая сумма двух замкнутых линейных подпространств M и N, то двойственное X ′ к X изоморфно прямой сумме двойников M и N. Если M - замкнутое линейное подпространство в X можно сопоставить ортогонал M в двойственном,

$M\; \perp \; =\; \{x\; \prime \; \in \; X\; \prime :\; x\; \prime \; (m)\; =\; 0,\; \forall \; m\; \in \; M\}.\; \{\backslash \; displaystyle\; M\; ^\; \{\backslash \; perp\}\; =\; \backslash \; left\; \backslash \; \{x\; \text{'}\backslash \; in\; X\text{'}:\; x\; \text{'}(m)\; =\; 0,\; \backslash \; \backslash \; forall\; m\; \backslash \; in\; M\; \backslash \; right\; \backslash \}.\}$

Ортогональный M является замкнутое линейное подпространство двойственного. Двойник к M изометрически изоморфен X ′ / M. Двойственный к X / M изометрически изоморфен M.

Двойственный к сепарабельному банахову пространству не обязательно должен быть сепарабельным, но:

Теорема. Пусть X - нормированное пространство. Если X 'разделимо, то X разделимо.

Когда X' разделимо, вышеупомянутый критерий для совокупности может использоваться для доказательства существования счетного полного подмножества в X.

Слабые топологии

Слабая топология на банаховом пространстве X - это грубейшая топология на X, для которой все элементы x ′ в непрерывное сопряженное пространство X ′ непрерывны. Следовательно, нормальная топология тоньше, чем слабая топология. Из теоремы Хана – Банаха об отделимости следует, что слабой топологией является хаусдорф и что замкнутое по норме выпуклое подмножество банахова пространства также слабо замкнуто. Непрерывное по норме линейное отображение между двумя банаховыми пространствами X и Y также слабо непрерывно, т. Е. Непрерывно от слабой топологии X к топологии Y.

Если X бесконечномерно, существуют линейные отображения, которые не являются непрерывными. Пространство X всех линейных отображений из X в основное поле K (это пространство X называется алгебраическим двойственным пространством, чтобы отличить его от X ′) также индуцирует топологию на X которая точнее, чем слабая топология, и гораздо реже используется в функциональном анализе.

На дуальном пространстве X 'существует топология более слабая, чем слабая топология X', называемая слабой * топологией. Это самая грубая топология на X ′, для которой все оценочные отображения x ′ ∈ X ′ → x ′ (x), x ∈ X, непрерывны. Его важность проистекает из теоремы Банаха – Алаоглу.

теоремы Банаха – Алаоглу. Пусть X - нормированное векторное пространство. Тогда закрытый единичный шар B ′ = {x ′ ∈ X ′: || x ′ || ≤ 1} двойственного пространства компактно в слабой * топологии.

Теорема Банаха – Алаоглу зависит от теоремы Тихонова о бесконечных произведениях компактных пространств. Когда X отделимо, единичный шар B 'двойственного является метризуемым компактом в слабой * топологии.

Примеры двойственных пространств

Двойственное к c 0 изометрически изоморфен ℓ: для любого ограниченного линейного функционала f на c 0 существует единственный элемент y = {y n } ∈ ℓ такой, что

$f\; (x)\; =\; \sum \; n\; \in \; N\; xnyn,\; x\; =\; \{xn\}\; \in \; c\; 0\; и\; \Vert \; f\; \Vert \; (c\; 0)\; \prime \; =\; \Vert \; y\; \Vert \; \ell \; 1.\; \{\backslash \; displaystyle\; f\; (x)\; =\; \backslash \; sum\; \_\; \{n\; \backslash \; in\; \backslash \; mathbf\; \{N\}\}\; x\_\; \{n\}\; y\_\; \{n\},\; \backslash \; qquad\; x\; =\; \backslash \; \{x\_\; \{n\}\; \backslash \}\; \backslash \; in\; c\_\; \{0\},\; \backslash \; \backslash \; \{\backslash \; text\; \{and\}\}\; \backslash \; \backslash \; \backslash \; |\; f\; \backslash \; |\; \_\; \{(c\_\; \{0\})\; \text{'}\}\; =\; \backslash \; |\; y\; \backslash \; |\; \_\; \{\backslash \; ell\; \_\; \{1\}\}.\}$

Двойник - изометрически изоморфна. Двойственное к L ([0, 1]) изометрически изоморфно L ([0, 1]), когда 1 ≤ p < ∞ and 1/p + 1/q = 1.

Для каждого вектора y в гильбертовом пространстве H отображение

$x\; \in \; H\; \to \; fy\; (x)\; =\; ⟨x,\; y⟩\; \{\backslash \; displaystyle\; x\; \backslash \; in\; H\; \backslash \; to\; f\_\; \{y\}\; (x)\; =\; \backslash \; langle\; x,\; y\; \backslash \; rangle\}$

определяет непрерывный линейный функционал f y на H. Теорема Рисса о представлении утверждает, что каждый непрерывный линейный функционал на H имеет вид f y для однозначно определенного вектора y в H. Отображение y ∈ H → f y - это антилинейная изометрическая биекция из H на двойственную ему H ′. Когда скаляры действительны, это отображение является изометрическим изоморфизмом.

Когда K - компактное хаусдорфово топологическое пространство, двойственное M (K) к C (K) - это пространство радоновских мер в смысле Бурбаки. Подмножество P (K) в M (K), состоящее из неотрицательных мер массы 1 (вероятностных мер ), является выпуклым w * -замкнутым подмножеством единичного шара в M (K). крайними точками P (K) являются меры Дирака на K. Множество мер Дирака на K, снабженное w * -топологией, гомеоморфно к K.

Теорема Банаха – Стоуна. Если K и L - компактные хаусдорфовы пространства и если C (K) и C (L) изометрически изоморфны, то топологические пространства K и L гомеоморфный.

Результат был расширен Амиром и Камберном на случай, когда мультипликативное расстояние Банаха – Мазура между C (K) и C (L) равно < 2. The theorem is no longer true when the distance is = 2.

в коммутативном Банахова алгебра C (K), максимальные идеалы являются в точности ядрами мер Дирака на K,

$I\; x\; =\; ker\; \; \delta \; x\; =\; \{f\; \in \; C\; (K):\; f\; (\; x)\; =\; 0\},\; x\; \in \; K.\; \{\backslash \; displaystyle\; I\_\; \{x\}\; =\; \backslash \; ker\; \backslash \; delta\; \_\; \{x\}\; =\; \backslash \; \{f\; \backslash \; in\; C\; (K):\; f\; (x)\; =\; 0\; \backslash \},\; \backslash \; quad\; x\; \backslash \; in\; K.\}$

В общем, по теореме Гельфанда – Мазура максимальные идеалы унитальной коммутативной банаховой алгебры можно отождествить с ее символами - не просто как множества, но как топологические пространства: первые с топология оболочка-ядро и последняя с топологией w *. В этом отождествлении максимальное идеальное пространство можно рассматривать как w * -компактное подмножество единичного шара в двойственном A '.

Теорема. Если K - компактное хаусдорфово пространство, то пространство максимальных идеалов Ξ банаховой алгебры C (K) гомеоморфно K.

Не всякая коммутативная банахова алгебра с единицей имеет вид C (K) для некоторого компактного хаусдорфова пространства K. Однако это утверждение верно, если поместить C (K) в меньшую категорию коммутативных C * -алгебр. Теорема Гельфанда о представлении для коммутативных C * -алгебр утверждает, что каждая коммутативная унитальная C * -алгебра A изометрически изоморфна C (K) пространству. Хаусдорфово пространство K здесь снова является пространством максимальных идеалов, также называемым спектром алгебры A в контексте C * -алгебры.

Двуал

Если X - нормированное пространство, (непрерывный) двойственный X ′ ′ двойного X ′ называется двунаправленным или вторым двойственным X. Для любого нормированного пространства X существует естественное отображение

$\{FX:\; X\; \to \; X\; ″\; FX\; (x)\; (f)\; =\; f\; (x)\; \forall \; x\; \in \; X,\; \forall \; f\; \in \; X\; \prime \; \{\; \backslash \; Displaystyle\; \{\backslash \; begin\; \{cases\}\; F\_\; \{X\}:\; X\; \backslash \; to\; X\; \text{'}\text{'}\; \backslash \backslash \; F\_\; \{X\}\; (x)\; (f)\; =\; f\; (x)\; \backslash \; forall\; x\; \backslash \; in\; X,\; \backslash \; forall\; f\; \backslash \; in\; X\; \text{'}\backslash \; end\; \{cases\}\}\}$

Это определяет F X (x) как непрерывный линейный функционал на X ′, то есть элемент X ′ ′. Отображение F X : x → F X (x) является линейным отображением от X до X ′ ′. Как следствие существования нормирующего функционала f для каждого x в X, это отображение F X изометрично, поэтому инъективно.

Например, двойственное X = c 0 отождествляется с, а двойственное к отождествляется с ℓ, пространством ограниченных скалярных последовательностей. Под этими идентификациями F X - это карта включения от c 0 до ℓ. Он действительно изометрический, но не на.

Если F X является сюръективным, то нормированное пространство X называется рефлексивным (см. ниже ). Будучи двойственным к нормированному пространству, двузначное X ′ ′ полно, поэтому каждое рефлексивное нормированное пространство является банаховым пространством.

Используя изометрическое встраивание F X, принято рассматривать нормированное пространство X как подмножество его двумерного числа. Когда X - банахово пространство, оно рассматривается как замкнутое линейное подпространство в X ′ ′. Если X не рефлексивно, единичный шар X является собственным подмножеством единичного шара X ′ ′. Теорема Голдстайна утверждает, что единичный шар нормированного пространства слабо * -плотен в единичном шаре двузначного числа. Другими словами, для каждого x ′ ′ в двузначном выражении существует net {xj} в X, так что

$sup\; j\; \Vert \; xj\; \Vert \; \le \; \Vert \; x\; ″\; \Vert ,\; x\; ″\; (f)\; =\; lim\; jf\; (xj),\; f\; \in \; X\; \prime .\; \{\backslash \; Displaystyle\; \backslash \; sup\; \_\; \{j\}\; \backslash \; |\; x\_\; \{j\}\; \backslash \; |\; \backslash \; leq\; \backslash \; |\; x\; \text{'}\text{'}\; \backslash \; |,\; \backslash \; \backslash \; x\; \text{'}\text{'}\; (f)\; =\; \backslash \; lim\; \_\; \{j\}\; f\; (x\_\; \{j\}),\; \backslash \; quad\; f\; \backslash \; in\; X\; \text{'}.\}$

Сеть может быть заменена слабо * -сходящейся последовательностью, когда двойственное X' отделимо. С другой стороны, элементы двузначного числа, не входящие в ℓ, не могут быть слабым * -пределом последовательностей в, так как ℓ является слабо последовательно полными.

теоремами Банаха

Вот Основные общие результаты о банаховых пространствах, которые восходят к временам книги Банаха (Banach (1932)) и связаны с теоремой Бэра о категориях. Согласно этой теореме полное метрическое пространство (например, банахово пространство, пространство Фреше или F-пространство ) не может быть равно объединению счетного числа замкнутых подмножеств с пустыми интерьеры. Следовательно, банахово пространство не может быть объединением счетного числа замкнутых подпространств, если оно уже не равно одному из них; банахово пространство со счетным базисом Гамеля конечномерно.

Теорема Банаха – Штейнгауза. Пусть X - банахово пространство, а Y - нормированное векторное пространство. Предположим, что F - набор непрерывных линейных операторов из X в Y. Принцип равномерной ограниченности утверждает, что если для всех x в X выполняется sup T∈F || T (x) || Y< ∞, then supT∈F || T || Y< ∞.

Теорема Банаха – Штейнгауза не ограничивается банаховыми пространствами. Его можно распространить, например, на случай, когда X является пространством Фреше, при условии, что вывод изменен следующим образом: при той же гипотезе существует окрестность U 0 в X такая, что все T в F равномерно ограничены на U,

Теорема об открытом отображении. Пусть X и Y банаховы пространства и T: X → Y - сюръективный непрерывный линейный оператор, то T - открытое отображение.

Следствие. Любой взаимно однозначный ограниченный линейный оператор из банахова пространства на банахово пространство является изоморфизмом.

Первая теорема об изоморфизме для банаховых пространств. Предположим, что X и Y - банаховы пространства и T ∈ B (X, Y). Предположим далее, что образ T замкнут в Y. Тогда X / Ker (T) изоморфно T (X).

Этот результат является прямым следствием предыдущей теоремы об изоморфизме Банаха и канонической факторизации ограниченных линейных карты.

Следствие. Если банахово пространство X является внутренней прямой суммой замкнутых подпространств M 1,..., M n, то X изоморфно M 1 ⊕... ⊕ M n.

Это еще одно следствие теоремы Банаха об изоморфизме, примененное к непрерывной биекции из M 1 ⊕... ⊕ M n на X, отправляя (m 1,..., m n) на сумму m 1 +... + m n.

Замкнутый график Теорема. Пусть T: X → Y - линейное отображение между банаховыми пространствами. График T замкнут в X × Y тогда и только тогда, когда T непрерывен.

Рефлексивность

Нормированное пространство X называется рефлексивным, когда естественное карта

$\{FX:\; X\; \to \; X\; ″\; FX\; (x)\; (f)\; =\; f\; (x)\; \forall \; x\; \in \; X,\; \forall \; f\; \in \; X\; \prime \; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{cases\}\; F\_\; \{X\}:\; X\; \backslash \; to\; X\; \text{'}\text{'}\; \backslash \backslash \; F\_\; \{X\}\; (x)\; (f)\; =\; f\; (x)\; \backslash \; forall\; x\; \backslash \; in\; X,\; \backslash \; forall\; f\; \backslash \; in\; X\; \text{'}\backslash \; end\; \{ases\}\}$

сюръективно. Рефлексивные нормированные пространства - это банаховы пространства.

Теорема. Если X - рефлексивное банахово пространство, каждое замкнутое подпространство X и каждое фактор-пространство X рефлексивны.

Это следствие теоремы Хана – Банаха. Далее, по теореме об открытом отображении, если существует ограниченный линейный оператор из банахова пространства X на банахово пространство Y, то Y рефлексивен.

Теорема. Если X - банахово пространство, то X рефлексивно тогда и только тогда, когда X ′ рефлексивно.

Следствие. Пусть X - рефлексивное банахово пространство. Тогда X сепарабельно тогда и только тогда, когда X ′ сепарабелен.

В самом деле, если двойственное Y ′ банахова пространства Y сепарабельно, то Y сепарабельно. If X is reflexive and separable, then the dual of X ′ is separable, so X ′ is separable.

Theorem.Suppose that X1,..., Xnare normed spaces and that X = X1⊕... ⊕ Xn. Then X is reflexive if and only if each Xjis reflexive.

Hilbert spaces are reflexive. The L spaces are reflexive when 1 < p < ∞. More generally, uniformly convex spaces are reflexive, by the Milman–Pettis theorem. The spaces c0, ℓ, L([0, 1]), C([0, 1]) are not reflexive. In these examples of non-reflexive spaces X, the bidual X ′′ is "much larger" than X. Namely, under the natural isometric embedding of X into X ′′ given by the Hahn–Banach theorem, t Фактор X ′ ′ / X бесконечномерен и даже неразделим. Однако Роберт С. Джеймс построил пример нерефлексивного пространства, обычно называемого «пространством Джеймса» и обозначаемого J, такое, что фактор J ′ ′ / J является одномерным. Более того, это пространство J изометрически изоморфно своему бидуалу.

Теорема. Банахово пространство X рефлексивно тогда и только тогда, когда его единичный шар компактен в слабой топологии.

Когда X рефлексивно, отсюда следует, что все замкнутые и ограниченные выпуклые подмножества в X слабо компактны. В гильбертовом пространстве H слабая компактность единичного шара очень часто используется следующим образом: любая ограниченная последовательность в H имеет слабо сходящиеся подпоследовательности.

Слабая компактность единичного шара предоставляет инструмент для поиска решений в рефлексивных пространствах некоторых задач оптимизации. Например, каждая выпуклая непрерывная функция на единичном шаре B рефлексивного пространства достигает своего минимума в некоторой точке в B.

Как частный случай предыдущего результата, когда X является в рефлексивном пространстве над R каждый непрерывный линейный функционал f в X ′ достигает своего максимума || f || на единичном шаре X. Следующая теорема Роберта С. Джеймса дает обратное утверждение.

Теорема Джеймса. Для банахова пространства следующие два свойства эквивалентны:

• X рефлексивно.
• для всех f в X ′ существует x в X с | | x || ≤ 1, так что f (x) = || f ||.

Теорема может быть расширена, чтобы дать характеристику слабо компактных выпуклых множеств.

На каждом нерефлексивном банаховом пространстве X существуют непрерывные линейные функционалы, не достигающие нормы. Однако теорема Бишопа - Фелпса утверждает, что функционалы, достигающие нормы, плотны по норме в двойственном X ′ к X.

Слабые сходимости последовательностей

Последовательность {x n } в банаховом пространстве X слабо сходится к вектору x ∈ X, если f (x n) сходится к f ( x) для любого непрерывного линейного функционала f из двойственного X ′. Последовательность {x n } является слабо последовательностью Коши, если f (x n) сходится к скалярному пределу L (f) для каждого f в X ′. Последовательность {f n } в двойственном X ′ слабо * сходится к функционалу f ∈ X ′, если f n (x) сходится к f ( x) для любого x из X. Слабо-сходящиеся и слабо * сходящиеся последовательности ограничены по норме как следствие теоремы Банаха – Штейнхауза.

Когда последовательность {x n } в X является слабо последовательностью Коши, предел L, указанный выше, определяет ограниченный линейный функционал на двойственном X ', т. Е. Элемент L двузначного X, а L - предел {x n } в слабой * -топологии двузначного числа. Банахово пространство X является слабо секвенциально полным, если каждая слабо сходящаяся в X последовательность Коши. Из предыдущего обсуждения следует, что рефлексивные пространства слабо секвенциально полны.

Теорема. Для любой меры μ пространство L (μ) является слабо секвенциально полным.

Ортонормированная последовательность в гильбертовом пространстве - простой пример слабо сходящейся последовательности с пределом, равным 0 вектор. Базис единичного вектора из ℓ, 1 < p < ∞, or of c0является другим примером слабо нулевой последовательности, то есть последовательности, которая слабо сходится к 0 . Для каждой слабо нулевой последовательности в банаховом пространстве существует последовательность выпуклых комбинаций векторов из данной последовательности, сходящаяся по норме к 0.

Базис единичных векторов в ℓ не является слабо Коши. Слабо последовательности Коши в слабо сходятся, так как L-пространства слабо секвенциально полны. На самом деле, слабо сходящиеся последовательности в сходятся по норме. Это означает, что ℓ удовлетворяет свойству Шура..

Результаты, включающие базис

Слабые последовательности Коши и базис are, являются противоположными случаями дихотомии, установленной в следующем глубоком результате HP Rosenthal.

Теорема. Пусть {x n } - ограниченная последовательность в банаховом пространстве. Либо {x n } имеет слабо подпоследовательность Коши, либо допускает подпоследовательность , эквивалентную стандартную базису единичных векторов ℓ.

Дополнение к этому результату принадлежит Оделлу и Розенталь (1975).

Теорема. Пусть X - сепарабельное банахово пространство. Следующие эквивалентны:

• Пространство X не содержит замкнутого подпространства, изоморфного ℓ.
• Каждый элемент двумерного X ′ ′ является слабым * -пределом отслеживает {x n } в X.

По теореме Голдстайна каждый элемент единичного шара B ′ ′ в X ′ ′ является слабым * -пределом сети в единичном шаре X. Когда X не содержат ℓ, элемент B ′ ′ является слабым * -пределом следовать в единичном шаре X.

Когда банахово пространство X отделимо, единичный шар двойного X ′, снабженный * -топология, является метризуемым компактным пространством K, и элемент x ′ ′ в двузначном X ′ ′ определяет ограниченную каждую функцию на K:

$x\; \prime \; \in \; K\; \mapsto \; x\; ″\; (x\; \prime ),\; |\; x\; ″\; (x\; \prime )\; |\; \le \; \Vert \; x\; ″\; \Vert .\; \{\backslash \; displaystyle\; x\; \text{'}\backslash \; in\; K\; \backslash \; mapsto\; x\text{'}\; \text{'}(x\text{'}),\; \backslash \; quad\; \backslash \; left\; |\; х\; \text{'}\text{'}\; (х\; \text{'})\; \backslash \; право\; |\; \backslash \; leq\; \backslash \; left\; \backslash \; |\; x\; \text{'}\text{'}\; \backslash \; right\; \backslash \; |.\}$

Эта функция непрерывна для компактной топологии K тогда и только тогда, когда x ′ ′ действительно находится в X, рассматриваемом как подмножество X ′ ′. Предположим дополнительно для остальной части абзаца, что X не содержит. Согласно предыдущему результату Оделла и Розенталя, функция x ′ ′ является поточечным пределом на K следить {x n } ⊂ X непрерывных функций на K, поэтому она является первой функцией класса Бэра на K. Единичный шарнир двузначного числа представляет точечно компактное подмножество первого класса Бэра на K.

Последовательность, слабые и слабые * компактность

Когда X сепарабельно, единичный шар дуального является слабым * -компактным по Банаху - Алаоглу и метризуемым для слабой * топологии, следовательно, любая ограниченная последовательность в государственном двойном слабо * сходящиеся подпоследовательности. Это применимо к сепарабельным рефлексивным пространствам, но в этом случае верно больше, как указано ниже.

Слабая топология банахова пространства X метризуема тогда и только тогда, когда X предназначено. Если двойное X ′ сепарабельно, слабая топология единичного шара X метризуема. В частности, это относится к сепарабельным рефлексивным банаховым пространствам. Хотя слабая топология единичного шара, вообще говоря, не является метризуемой, слабую компактность можно охарактеризовать с помощью последовательностей.

Теорема Эберлейна - Шмулиана. Множество A в банаховом взаимодействии относительно слабо компактно тогда, когда последовательность имеет последовательность {a n } в слабо сходящейся подпоследовательности.

Банахово X рефлексивно тогда и только тогда, когда каждое ограниченное пространство в X имеет слабо сходящуюся подпоследовательность.

Слабо компактное подмножество A в компактно по норме. Действительно, каждая последовательность в A имеет слабо сходящиеся подпоследовательности по Эберлейну - Шмулиану, сходящиеся по норме в силу свойств Шура следуют.

A Базис Шаудера в банаховом пространстве X - это последовательность {e n}n ≥ 0 векторов в X со своимством, что для каждого вектора x в X, существуют однозначно современные скаляры {x n}n ≥ 0, зависящие от x, такие, что

$x\; =\; \sum \; n\; =\; 0\; \infty \; xnen,\; т.\; е.\; x\; =\; lim\; n\; P\; n\; (x),\; P\; n\; (x):\; =\; \sum \; k\; =\; 0\; nxkek.\; \{\backslash \; displaystyle\; x\; =\; \backslash \; sum\; \_\; \{n\; =\; 0\}\; ^\; \{\backslash \; infty\}\; x\_\; \{n\}\; e\_\; \{n\},\; \backslash \; quad\; \{\backslash \; textit\; \{т.е.\}\}\; \backslash \; quad\; x\; =\; \backslash \; lim\; \_\; \{n\}\; P\_\; \{n\}\; (x),\; \backslash \; P\_\; \{n\}\; (x):\; =\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; ^\; \{n\}\; x\_\; \{k\}\; e\_\; \{k\}.\}$

Банаховы пространства с базисом Шаудера обязательно посредством счетного множества конечных линейных комбинаций с рациональными коэффициентами (скажем) плотно.

Из теоремы Банаха - Штейнгауза следует, что линейные представления {P n } равномерно ограничены некоторой константой C. Пусть {e. n} обозначает координатные функции, которые присваиваются каждый x в X - координата x n x в приведенном выше расширении. Их называют биортогональными функционалами . Когда базисные стандарты имеют норму 1, координатные функционалы {e. n} имеют норму ≤ 2C в двойном к X.

Большинство классических разделимых пространств имеют явные базы. Система Хаара {hn} является базисом для L ([0, 1]), 1 ≤ p <∞. тригонометрическая система является базисом в L (T ), когда 1 < p < ∞. The система Шаудера является базисом в пространстве C ([0, 1]). Вопрос о том, имеет ли дисковая алгебра A (D ) базис, оставался открытым более сорока лет, пока Бочкарев не показал в 1974 году, что A (D ) допускает базис, построенный из Система Франклина.

всегда каждый вектор x в банахном пространстве X с базисом является пределом P n (x), причем P n конечного ранга и пространно ограничено, пространство X удовлетворяет свойству ограниченная аппроксимации. Первый пример Энфло пространства, не обладающего своим аппроксимацией, был в то же время первым примером сепарабельного банахова пространства без базиса Шаудера.

Роберт С. Джеймс охарактеризовал рефлексивность в банахе пространства с базисом: пространство X с базисом Шаудера рефлексивно тогда и только тогда, когда базис является сжимающимся и ограниченно полным. В этом случае биортогональные функционалы образуют базис двойного к X.

Пусть X и Y - два K -векторных пространств. тензорное произведение X ⊗ Y элементов X и Y является K -векторным пространством Z с билинейным отображением T: X × Y → Z, обладающим следующим универсальным свойством :

Если T 1 : X × Y → Z 1 - любое билинейное отображение в K -векторное пространство существует Z 1, то единственное линейное отображение f: Z → Z 1 такое, что T 1 = f ∘ T.

Образ под T пары (x, y) в X × Y обозначается x ⊗ y и называется простым тензором . Каждый элемент z в X ⊗ Y является конечной суммой таких простых тензоров.

Существуют нормы, которые могут быть применены к тензорному произведению лежащих в основе векторных пространств, среди прочего проективная перекрестная норма и инъективная перекрестная норма, введенная А. Гротендик в 1955 году.

В общем, тензорное произведение полных пространств снова является не полным. При работе с банаховыми пространствами принято говорить, что проективное тензорное произведение двух банаховых пространств X и Y является пополнением $X\; \otimes \; ^\; \pi \; Y\; \{\backslash \; displaystyle\; X\; \{\backslash \; widehat\; \{\backslash \; otimes\}\}\; \_\; \{\backslash \; pi\; \}\; Y\}$алгебраического тензорного произведения X ⊗ Y, снабженного проективной тензорной нормой, и аналогично для инъективного тензорного произведения $X\; \otimes \; ^\; \epsilon \; Y\; \{\backslash \; displaystyle\; X\; \{\backslash \; widehat\; \{\backslash \; otimes\}\}\; \_\; \{\backslash \; varepsilon\}\; Y\}$. Гротендик доказал, в частности, что

$C\; (K)\; \otimes \; ^\; \epsilon \; Y\; \simeq \; C\; (K,\; Y),\; L\; 1\; ([0,\; 1])\; \otimes \; ^\; \pi \; Y\; \simeq \; L\; 1\; ([0,\; 1],\; Y),\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; C\; (K)\; \{\backslash \; widehat\; \{\backslash \; otimes\}\}\; \_\; \{\backslash \; varepsilon\}\; Y\; \backslash \; simeq\; C\; (K,\; Y),\; \backslash \backslash \; L\; ^\; \{1\}\; ([0,\; 1])\; \{\backslash \; widehat\; \{\backslash \; otimes\}\}\; \_\; \{\backslash \; pi\}\; Y\; \backslash \; simeq\; L\; ^\; \{1\}\; ([0,1],\; Y),\; \backslash \; end\; \{align\}\}\}$

где K - компактное хаусдорфово пространство, C (K, Y) банахово пространство непрерывных функций из K в Y и L ([0, 1], Y) пространство измеримых по Бохнеру и интегрируемых функций из [0, 1] в Y, причем изоморфизмы изометричны. Два приведенных выше изоморфизма реализуются расширениями карты, переводящей тензор f ⊗ y в вектор-функцию s ∈ K → f (s) y ∈ Y.

Теневые произведения и свойство аппроксимации

Пусть X - банахово пространство. Тензорное произведение $X\; \prime \; \otimes \; ^\; \epsilon \; X\; \{\backslash \; displaystyle\; X\; \text{'}\{\backslash \; widehat\; \{\backslash \; otimes\}\}\; \_\; \{\backslash \; varepsilon\}\; X\}$изометрически идентифицируется с замыканием в B (X) множеством операторов конечного ранга. Когда X имеет свойство аппроксимации, это замыкание совпадает с пространством компактных операторов на X.

Для любого банахова пространства Y существует естественная норма 1 линейная карта

$Y\; \otimes \; ^\; \pi \; X\; \to \; Y\; \otimes \; ^\; \epsilon \; X\; \{\backslash \; displaystyle\; Y\; \{\backslash \; widehat\; \{\backslash \; otimes\}\}\; \_\; \{\backslash \; pi\}\; X\; \backslash \; to\; Y\; \{\backslash \; widehat\; \{\backslash \; otimes\}\}\; \_\; \{\backslash \; varepsilon\}\; X\}$

, полученный расширением тождественного отображения алгебраического тензорного произведения. Гротендик связующей проблемы является ли это отображение взаимно однозначным, когда Y является двойным двойным X. Точно, для каждого банахова пространства X отображение

$X\; \prime \; \otimes \; ^\; \pi \; Икс\; ⟶\; Икс\; \prime \; \otimes \; ^\; \epsilon \; Икс\; \{\backslash \; Displaystyle\; X\; \text{'}\{\backslash \; widehat\; \{\backslash \; otimes\}\}\; \_\; \{\backslash \; pi\}\; X\; \backslash \; \backslash \; longrightarrow\; X\text{'}\; \{\backslash \; widehat\; \{\backslash \; otimes\}\}\; \_\; \{\backslash \; varepsilon\}\; X\}$

взаимно однозначно тогда и только тогда, когда X обладает своим аппроксимации.

Гротендик предположил, что $X\; \otimes \; ^\; \pi \; Y\; \{\backslash \; displaystyle\; X\; \{\backslash \; widehat\; \{\backslash \; otimes\}\}\; \_\; \{\backslash \; pi\}\; Y\}$и $X\; \otimes \; ^\; \epsilon \; Y\; \{\backslash \; displaystyle\; X\; \{\backslash \; widehat\; \{\backslash \; otimes\}\}\; \_\; \{\backslash \; varepsilon\}\; Y\}$должны быть разными, если X и Y бесконечномерные банаховы пространства. Это было опровергнуто Жилем Пизье в 1983 году. Пизье построил бесконечномерное банахово пространство X такое, что $X\; \otimes \; ^\; \pi \; X\; \{\backslash \; displaystyle\; X\; \{\backslash \; widehat\; \{\backslash \; otimes\}\}\; \_\; \{\backslash \; pi\}\; X\}$и $X\; \otimes \; ^\; \epsilon \; X\; \{\backslash \; displaystyle\; X\; \{\backslash \; widehat\; \{\backslash \; otimes\}\}\; \_\; \{\backslash \; varepsilon\}\; X\}$равны. Более, как и в примере Энфло, это пространство X является пространством "ручной работы", которое не имеет свойств того аппроксимации. С другой стороны, Шанковский доказал, что классическое пространство B (ℓ) не обладает своим аппроксимации.

Характеризация гильбертова пространства среди банаховых пространств

Необходимым и достаточным условием сопоставления норм банахова пространства X со скалярным произведением тождество параллелограмма :

$\forall \; x,\; y\; \in \; X:\; \Vert \; x\; +\; y\; \Vert \; 2\; +\; \Vert \; x\; -\; y\; \Vert \; 2\; =\; 2\; (\Vert \; x\; \Vert \; 2\; +\; \Vert \; y\; \Vert \; 2).\; \{\backslash \; displaystyle\; \backslash \; forall\; x,\; y\; \backslash \; in\; X:\; \backslash \; qquad\; \backslash \; |\; х\; +\; у\; \backslash \; |\; ^\; \{2\}\; +\; \backslash \; |\; ху\; \backslash \; |\; ^\; \{2\}\; =\; 2\; \backslash \; left\; (\backslash \; |\; x\; \backslash \; |\; ^\; \{2\}\; +\; \backslash \; |\; y\; \backslash \; |\; ^\; \{2\}\; \backslash \; right).\}$

Отсюда следует, например, что пространство Лебега L ([0, 1]) является гильбертовым пространством только тогда, когда p = 2, когда эта идентичность удовлетворяется, внутренний продукт задается поляризационной идентичностью . В случае вещественных скаляров это дает:

$⟨x,\; y⟩\; =\; 1\; 4\; (\Vert \; x\; +\; y\; \Vert \; 2\; -\; \Vert \; x\; -\; y\; \Vert \; 2).\; \{\backslash \; displaystyle\; \backslash \; langle\; x,\; y\; \backslash \; rangle\; =\; \{\backslash \; tfrac\; \{1\}\; \{4\}\}\; \backslash \; left\; (\backslash \; |\; x\; +\; y\; \backslash \; |\; ^\; \{2\}\; -\; \backslash \; |\; xy\; \backslash \; |\; ^\; \{2\}\; \backslash \; right).\}$

Для сложных скаляров, определяя внутренний продукт так, чтобы он был C -линейным по x, антилинейным по y, идентичность поляризации дает:

$⟨X,\; y⟩\; =\; 1\; 4\; (\Vert \; x\; +\; y\; \Vert \; 2\; -\; \Vert \; x\; -\; y\; \Vert \; 2\; +\; i\; (\Vert \; x\; +\; iy\; \Vert \; 2\; -\; \Vert \; x\; -\; iy\; \Vert \; 2)).\; \{\backslash \; displaystyle\; \backslash \; langle\; x,\; y\; \backslash \; rangle\; =\; \{\backslash \; tfrac\; \{1\}\; \{4\}\}\; \backslash \; left\; (\backslash \; |\; x\; +\; y\; \backslash \; |\; ^\; \{2\}\; -\; \backslash \; |\; xy\; \backslash \; |\; ^\; \{2\}\; +\; i\; \backslash \; left\; (\; \backslash \; |\; x\; +\; iy\; \backslash \; |\; ^\; \{2\}\; -\; \backslash \; |\; x-iy\; \backslash \; |\; ^\; \{2\}\; \backslash \; right)\; \backslash \; right).\}$

Чтобы убедиться в достаточности закона параллелограмма, в вещественном случае наблюдаем, что < x, y>является симметричным, а в сложном случае удовлетворяет свойству эрмитовой симметрии и < ix, y>= i < x, y>. Из закона параллелограмма следует, что < x, y>аддитивен по x. Отсюда следует, что она линейна по рациональным числам, а значит, линейна по непрерывности.

Доступно несколько характеристик пространств, изоморфных (а не изометричных) гильбертовым пространствам. Закон может быть расширен более чем на два случая и ослаблен введением двустороннего неравенства с константой c ≥ 1: Квапень доказал, что если

$c\; -\; 2\; \sum \; k\; =\; 1\; n\; \Vert \; xk\; \Vert \; 2\; \le \; Ave\; \pm \; \; \Vert \; \sum \; К\; знак\; равно\; 1\; n\; \pm \; xk\; \Vert \; 2\; \le \; с\; 2\; \sum \; К\; знак\; равно\; 1\; N\; \Vert \; xk\; \Vert \; 2\; \{\backslash \; displaystyle\; c\; ^\; \{-\; 2\}\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{n\}\; \backslash \; left\; \backslash \; |\; x\_\; \{k\}\; \backslash \; right\; \backslash \; |\; ^\; \{2\}\; \backslash \; leq\; \backslash \; operatorname\; \{Ave\}\; \_\; \{\backslash \; pm\}\; \backslash \; left\; \backslash \; |\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{n\}\; \backslash \; pm\; x\_\; \{k\}\; \backslash \; right\; \backslash \; |\; ^\; \{2\}\; \backslash \; leq\; c\; ^\; \{2\}\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{n\}\; \backslash \; left\; \backslash \; |\; x\_\; \{k\}\; \backslash \; right\; \backslash \; |\; ^\; \{2\}\}$

для любого целого числа n и всех семейств векторов {x 1,..., x n } ⊂ X, то банахово пространство X изоморфно гильбертову пространству. Здесь Ave ± обозначает среднее значение по возможности решения той возможности выбора знаков ± 1. В той же статье Квапень доказал, что справедливость банаховозначной теоремы Парсеваля для преобразования Фурье характеризует банахные гильбертовым пространствам.

Линденштраус и Цафрири доказали, что банахово пространство, в котором находится замкнутое линейное подпространство дополняется (то есть есть ограниченным образом линейного проектора), изоморфно гильбертову пространству. Доказательство опирается на теорему Дворецкого о евклидовых сечениях многомерных центрально-симметричных выпуклых тел. Другими словами, теорема Дворецкого утверждает, что для любого целого, любое конечное нормированное пространство с размерностью, достаточно большой по сравнению с n, содержит подпространства, почти изометричные n-мерному евклидову пространству.

Следующий результат дает решение так называемой задачи однородного пространства. Бесконечномерное банахово пространство X называется однородным, если оно изоморфно всем своим бесконечным замкнутым подпространствам. Банахово пространство, изоморфное, является однородным, и Банах требовал обратного.

Теорема. Банахово пространство, изоморфное всем своим бесконечным замкнутым подпространствам, изоморфно сепарабельному гильбертову пространству.

Бесконечное- размерное банахово пространство наследственно неразложимо, когда никакое его подпространство может быть изоморфно прямым сумме двух бесконечномерных банаховых пространств. Теорема о дихотомии Гауэрса утверждает, что любое бесконечное номерное банахово пространство X содержит либо подпространство Y с безусловным базисом, либо наследственно неразложимое подпространство Z, и, в частности, Z не изоморфно к его замкнутым гиплоерпскостям. Если X однороден, значит, он должен иметь безусловную основу. Тогда из частичного решения, полученного Коморовским и Томчаком - Ягерманом для пространств с безусловным базисом, следует, что X изоморфно.

Метрическая классификация

Если $T:\; X\; \to \; Y\; \{\backslash \; displaystyle\; T:\; X\; \backslash \; to\; Y\}$является изометрией из Банахово пространства $X\; \{\backslash \; displaystyle\; X\}$на банахово пространство $Y\; \{\backslash \; displaystyle\; Y\}$(где оба $X\; \{\backslash \; displaystyle\; X\}$и $Y\; \{\backslash \; displaystyle\; Y\}$- безопасность пространства над $R\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{R\}\}$), Теорема Мазура-Улама утверждает, что $T\; \{\backslash \; displaystyle\; T\}$должно быть аффинным преобразованием. В частности, если $T\; (0\; X)\; =\; 0\; Y\; \{\backslash \; displaystyle\; T\; (0\_\; \{X\})\; =\; 0\_\; \{Y\}\}$, это $T\; \{\backslash \; displaystyle\; T\}$сопоставляет ноль $X\; \{\backslash \; displaystyle\; X\}$с нулем $Y\; \{\backslash \; displaystyle\; Y\}$, $T\; \{\backslash \; displaystyle\; T\}$должен быть линейным. Этот результат означает, что метрика в банаховых пространствах, и в более общем плане в нормированных пространствах, полностью отражает их линейную структуру.

Топологическая классификация

Конечномерные бановы пространства гомеоморфны как топологические пространства, если и только если они имеют ту же размерность, что и реальные уровни пространства.

Теорема Андерсона - Кадека (1965–66) доказывает, что любые два бесконечномерных сепарабельных банаховых пространств гомеоморфны как топологические пространства. Теорема Кадека была расширена Торунчиком, который доказал, что любые два банаховых пространства гомеоморфны тогда и только тогда, когда они имеют одинаковый характер плотности, минимальную мощность плотного подмножества.

Пространства непрерывных функций

Когда два компактных хаусдорфовых пространства K 1 и K 2 гомеоморфны, банаховы пространства C (K 1) и C (K 2) изометричны. И наоборот, когда K 1 не гомеоморфно K 2, (мультипликативное) расстояние Банаха-Мазура между C (K 1) и C (K 2) должно быть больше или равно 2, см. Выше результаты Амира и Камберна. Хотя несчетные компактные метрические пространства могут иметь разные типы гомеоморфности, один из них получил следующий результат Милютина:

Теорема. Пусть K - несчетное компактное метрическое пространство. Тогда C (K) изоморфна C ([0, 1]).

Иная ситуация для счетно бесконечных компактных хаусдорфовых пространств. Каждый счетно-бесконечный компакт K гомеоморфен некоторому отрезку порядковых чисел

$⟨1,\; \alpha ⟩\; =\; \{\gamma :\; 1\; \le \; \gamma \; \le \; \alpha \}\; \{\backslash \; displaystyle\; \backslash \; langle\; 1,\; \backslash \; alpha\; \backslash \; rangle\; =\; \backslash \; \{\backslash \; gamma\; \backslash :\; \backslash \; 1\; \backslash \; leq\; \backslash \; gamma\; \backslash \; leq\; \backslash \; alpha\; \backslash \}\}$

с топологией порядка , где α - счетно бесконечный ординал. Тогда банахово пространство C (K) изометрично C (<1, α>). Когда α, β - два счетно бесконечных ординала и предполагая, что α ≤ β, пространства C (<1, α>) и C (<1, β>) изоморфны тогда и только тогда, когда β < α. For example, the Banach spaces

$C\; (⟨1,\; \omega ⟩),\; C\; (⟨1,\; \omega \; \omega ⟩),\; C\; (⟨1,\; \omega \; \omega \; 2⟩),\; C\; (⟨1,\; \omega \; \omega \; 3⟩),\; \cdots ,\; C\; (⟨1,\; \omega \; \omega \; \omega ⟩),\; \cdots \; \{\backslash \; displaystyle\; C\; (\backslash \; langle\; 1,\; \backslash \; omega\; \backslash \; rangle),\; \backslash \; C\; (\backslash \; langle\; 1,\; \backslash \; omega\; ^\; \{\backslash \; omega\}\; \backslash \; rangle),\; \backslash \; C\; (\backslash \; langle\; 1,\; \backslash \; omega\; ^\; \{\backslash \; omega\; ^\; \{2\}\}\; \backslash \; rangle),\; \backslash \; C\; (\backslash \; langle\; 1,\; \backslash \; omega\; ^\; \{\backslash \; omega\; ^\; \{3\}\}\; \backslash \; rangle),\; \backslash \; cdots,\; C\; (\backslash \; langle\; 1,\; \backslash \; omega\; ^\; \{\backslash \; omega\; ^\; \{\backslash \; omega\}\}\; \backslash \; rangle),\; \backslash \; cdots\; \}$

взаимно неизоморфны.

Словарь символов:

• K= R, C;
• X - компактное хаусдорфово пространство ;
• I - замкнутый и ограниченный интервал [a, b];
• p, q - действительные числа с 1 < p, q < ∞ so that 1/p + 1/q = 1.
• Σ - σ-алгебра множеств;
• Ξ - алгебра множеств ( для пространств, требующих только конечной аддитивности, таких как ba пространство );
• μ является мерой с вариацией | μ |.

Классические банаховы пространства
	Dual пробел	Рефлексивно	слабо последовательно завершено	Норма	Примечания
K	K	Да	Да	$\Vert \; x\; \Vert \; 2\; =\; (\sum \; i\; =\; 1\; n\; |\; xi\; |\; 2)\; 1\; /\; 2\; \{\backslash \; displaystyle\; \backslash \; |\; x\; \backslash \; |\; \_\; \{2\}\; =\; \backslash \; left\; (\backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; |\; x\_\; \{i\}\; |\; ^\; \{2\}\; \backslash \; right)\; ^\; \{1/2\}\}$	Евклидово пространство
ℓ. p	ℓ. q	Да	Да	$\Vert \; x\; \Vert \; p\; =\; (\sum \; i\; =\; 1\; n\; |\; xi\; |\; p)\; 1\; p\; \{\backslash \; displaystyle\; \backslash \; |\; x\; \backslash \; |\; \_\; \{p\}\; =\; \backslash \; left\; (\backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; |\; x\_\; \{i\}\; |\; ^\; \{p\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{1\}\; \{p\}\}\}$
ℓ. ∞	ℓ. 1	Да	Да	$\Vert \; Икс\; \Vert \; \infty \; =\; макс\; 1\; \le \; я\; \le \; N\; |\; xi\; |\; \{\backslash \; displaystyle\; \backslash \; |\; x\; \backslash \; |\; \_\; \{\backslash \; infty\}\; =\; \backslash \; max\; \backslash \; nolimits\; \_\; \{1\; \backslash \; leq\; i\; \backslash \; leq\; n\}\; |\; x\_\; \{i\; \}\; |\}$
ℓp	ℓq	Да	Да	$\Vert \; x\; \Vert \; p\; =\; (\sum \; i\; =\; 1\; \infty \; |\; xi\; |\; p)\; 1\; p\; \{\backslash \; dis\; playstyle\; \backslash \; |\; x\; \backslash \; |\; \_\; \{p\}\; =\; \backslash \; left\; (\backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{\backslash \; infty\}\; |\; x\_\; \{i\}\; |\; ^\; \{p\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{1\}\; \{\; p\}\; \}\}$
ℓ1	ℓ∞	No	Да	$\Vert \; x\; \Vert \; 1\; =\; \sum \; i\; =\; 1\; \infty \; |\; х\; я\; |\; \{\backslash \; displaystyle\; \backslash \; |\; х\; \backslash \; |\; \_\; \{1\}\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{\backslash \; infty\}\; |\; x\_\; \{i\}\; |\}$
ℓ∞	ba	No	No	$\Vert \; x\; \Vert \; \infty \; =\; sup\; i\; |\; х\; я\; |\; \{\backslash \; Displaystyle\; \backslash \; |\; х\; \backslash \; |\; \_\; \{\backslash \; infty\}\; =\; \backslash \; sup\; \backslash \; nolimits\; \_\; \{i\}\; |\; x\_\; \{i\}\; |\}$
c	ℓ1	No	No	$\Vert \; x\; \Vert \; \infty \; =\; sup\; i\; |\; х\; я\; |\; \{\backslash \; displaystyle\; \backslash \; |\; х\; \backslash \; |\; \_\; \{\backslash \; infty\}\; =\; \backslash \; sup\; \backslash \; nolimits\; \_\; \{i\}\; |\; x\_\; \{i\}\; |\}$
c0	ℓ1	No	No	$\Vert \; x\; \Vert \; \infty \; =\; sup\; i\; |\; х\; я\; |\; \{\backslash \; displaystyle\; \backslash \; |\; х\; \backslash \; |\; \_\; \{\backslash \; infty\}\; =\; \backslash \; sup\; \backslash \; nolimits\; \_\; \{i\}\; |\; x\_\; \{i\}\; |\}$	Изоморфно, но не изометрично c.
bv	ℓ∞	No	Да	$\Vert \; x\; \Vert \; b\; v\; =\; |\; х\; 1\; |\; +\; \sum \; i\; =\; 1\; \infty \; |\; х\; я\; +\; 1\; -\; х\; я\; |\; \{\backslash \; displaystyle\; \backslash \; |\; х\; \backslash \; |\; \_\; \{bv\}\; =\; |\; x\_\; \{1\}\; |\; +\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{\backslash \; infty\}\; |\; x\_\; \{i\; +\; 1\}\; -x\_\; \{i\}\; |\}$	Изометрически изоморфно ℓ 1.
bv0	ℓ∞	No	Да	$\Vert \; x\; \Vert \; bv\; 0\; =\; \sum \; i\; =\; 1\; \infty \; |\; х\; я\; +\; 1\; -\; х\; я\; |\; \{\backslash \; displaystyle\; \backslash \; |\; х\; \backslash \; |\; \_\; \{bv\_\; \{0\}\}\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{\backslash \; infty\}\; |\; x\_\; \{i\; +\; 1\}\; -x\_\; \{i\}\; |\}$	Изометрически изоморфен ℓ 1.
bs	ba	No	No	$\Vert \; x\; \Vert \; bs\; =\; sup\; n\; |\; \sum \; i\; =\; 1\; n\; x\; i\; |\; \{\backslash \; displaystyle\; \backslash \; |\; х\; \backslash \; |\; \_\; \{bs\}\; =\; \backslash \; sup\; \backslash \; nolimits\; \_\; \{n\}\; \backslash \; left\; |\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; x\_\; \{i\}\; \backslash \; right\; |\}$	Изометрически изоморфно ℓ ∞.
cs	ℓ1	No	No	$\Vert \; x\; \Vert \; bs\; =\; sup\; n\; |\; \sum \; i\; =\; 1\; n\; x\; i\; |\; \{\backslash \; displaystyle\; \backslash \; |\; х\; \backslash \; |\; \_\; \{bs\}\; =\; \backslash \; sup\; \backslash \; nolimits\; \_\; \{n\}\; \backslash \; left\; |\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; x\_\; \{i\}\; \backslash \; right\; |\}$	Изометрически изоморфно c.
B (X, Ξ)	ba (Ξ)	No	No	$\Vert \; f\; \Vert \; B\; =\; sup\; x\; \in \; X\; |\; f\; (x)\; |\; \{\backslash \; Displaystyle\; \backslash \; |\; е\; \backslash \; |\; \_\; \{B\}\; =\; \backslash \; sup\; \backslash \; nolimits\; \_\; \{x\; \backslash \; in\; X\}\; |\; f\; (x)\; |\}$
C (X)	rca (X)	No	No	$\Vert \; x\; \Vert \; C\; (X)\; =\; max\; x\; \in \; X\; |\; f\; (x)\; |\; \{\backslash \; displaystyle\; \backslash \; |\; х\; \backslash \; |\; \_\; \{C\; (X)\}\; =\; \backslash \; max\; \backslash \; nolimits\; \_\; \{x\; \backslash \; in\; X\}\; |\; f\; (x)\; |\}$
ba (Ξ)	?	No	Да	$\Vert \; \mu \; \Vert \; Ba\; =\; sup\; A\; \in \; \Sigma \; |\; \mu \; |\; (A)\; \{\backslash \; displaystyle\; \backslash \; |\; \backslash \; mu\; \backslash \; |\; \_\; \{ba\}\; =\; \backslash \; sup\; \backslash \; nolimits\; \_\; \{A\; \backslash \; in\; \backslash \; Sigma\}\; |\; \backslash \; му\; |\; (A)\}$
ca (Σ)	?	No	Да	$\Vert \; {\rm M}\; \Vert \; ba\; =\; sup\; A\; \in \; \Sigma \; |\; \mu \; |\; (A)\; \{\backslash \; displaystyle\; \backslash \; |\; \backslash \; mu\; \backslash \; |\; \_\; \{ba\}\; =\; \backslash \; sup\; \backslash \; nolimits\; \_\; \{A\; \backslash \; in\; \backslash \; Sigma\}\; |\; \backslash \; му\; |\; (A)\}$	Замкнутое подпространство ba (Σ).
rca (Σ)	?	No	Да	$\Vert \; \mu \; \Vert \; b\; a\; =\; sup\; A\; \in \; \Sigma \; |\; \mu \; |\; (A)\; \{\backslash \; displaystyle\; \backslash \; |\; \backslash \; mu\; \backslash \; |\; \_\; \{ba\}\; =\; \backslash \; sup\; \backslash \; nolimits\; \_\; \{A\; \backslash \; in\; \backslash \; Sigma\}\; |\; \backslash \; му\; |\; (A)\}$	Замкнутое подпространство в ca (Σ).
L(μ)	L(μ)	Да	Да	$\Vert \; f\; \Vert \; p\; =\; (\int \; |\; f\; |\; pd\; \mu )\; 1\; p\; \{\backslash \; displaystyle\; \backslash \; |\; f\; \backslash \; |\; \_\; \{p\}\; =\; \backslash \; left\; (\backslash \; int\; |\; f\; |\; ^\; \{p\}\; \backslash ,\; d\; \backslash \; mu\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{1\}\; \{p\}\}\}$
L (μ)	L (μ)	No	Да	$\Vert \; f\; \Vert \; 1\; =\; \int \; |\; f\; |\; d\; \mu \; \{\backslash \; displaystyle\; \backslash \; |\; f\; \backslash \; |\; \_\; \{1\}\; =\; \backslash \; int\; |\; f\; |\; \backslash ,\; d\; \backslash \; mu\}$	Двойственное - L (μ), если μ σ-конечное.
BV ( I)	?	No	Да	$\Vert \; е\; \Vert \; BV\; =\; V\; f\; (I)\; +\; lim\; x\; \to \; a\; +\; f\; (x)\; \{\backslash \; displaystyle\; \backslash \; |\; f\; \backslash \; |\; \_\; \{BV\}\; =\; V\_\; \{f\}\; (I)\; +\; \backslash \; lim\; \backslash \; nolimits\; \_\; \{x\; \backslash \; to\; a\; ^\; \{+\}\}\; f\; (x)\}$	Vf(I) - это общая вариация f
NBV (I)	?	No	Да	$\Vert \; е\; \Vert \; BV\; =\; V\; е\; (I)\; \{\backslash \; displaystyle\; \backslash \; |\; f\; \backslash \; |\; \_\; \{BV\}\; =\; V\_\; \{f\}\; (I)\}$	NBV (I) состоит из функций BV (I), таких что $lim\; x\; \to \; a\; +\; f\; (x)\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; lim\; \backslash \; nolimits\; \_\; \{x\; \backslash \; to\; a\; ^\; \{+\}\}\; f\; (x)\; =\; 0\}$
AC (I)	K+ L (I)	No	Да	$\Vert \; е\; \Vert \; BV\; =\; V\; f\; (I)\; +\; lim\; x\; \to \; a\; +\; f\; (x)\; \{\backslash \; displaystyle\; \backslash \; |\; f\; \backslash \; |\; \_\; \{BV\}\; =\; V\_\; \{f\}\; (I)\; +\; \backslash \; lim\; \backslash \; nolimits\; \_\; \{x\; \backslash \; to\; a\; ^\; \{+\}\}\; f\; (x)\}$	Изоморфно пространству Соболева W (I).
C ([a, b])	rca ([a, b])	No	No	$\Vert \; f\; \Vert \; =\; \sum \; i\; =\; 0\; n\; sup\; x\; \in \; [a,\; b]\; |\; f\; (i)\; (x)\; |\; \{\backslash \; Displaystyle\; \backslash \; |\; е\; \backslash \; |\; =\; \backslash \; сумма\; \_\; \{я\; =\; 0\}\; ^\; \{n\}\; \backslash \; sup\; \backslash \; nolimits\; \_\; \{x\; \backslash \; in\; [a,\; b]\}\; \backslash \; left\; |\; f\; ^\; \{(i)\}\; (x)\; \backslash \; right\; |\}$	Изоморфно R ⊕ C ([a, b]), по существу, по теореме Тейлора.

Можно определить несколько концепций производной на банаховом пространстве. См. Статьи о производном от Фреше и о производном от Гато. Производная Фреше позволяет распространить понятие полной производной на банаховы пространства. Производная Гато позволяет расширить производную по направлению до локально выпуклых топологических векторных пространств. Дифференцируемость по Фреше - более сильное условие, чем дифференцируемость по Гато. квазипроизводная - это еще одно обобщение производной по направлениям, которое подразумевает более сильное условие, чем дифференцируемость по Гато, но более слабое, чем дифференцируемость по Фреше.

Несколько важных пространств в функциональном анализе, например, пространство всех бесконечно часто дифференцируемых функций R→ Rили пространство всех распределений на R полны, но не являются нормированными векторными пространствами и, следовательно, не банаховыми пространствами. В пространствах Фреше все еще есть полная метрика, а LF-пространства - это полные однородные векторные пространства, возникающие как пределы пространств Фреше.

• Пространство (математика) - Математическое множество с некоторой дополнительной структурой
  • Пространство Фреше - Локально выпуклое топологическое векторное пространство, которое также является полным метрическим пространством
  • Пространство Харди
  • Гильбертово пространство - внутреннее пространство произведения, которое является метрически полным; банахово пространство, норма которого индуцирует скалярное произведение (норма удовлетворяет тождеству параллелограмма)
  • L-полускалярное произведение - Обобщение скалярных произведений, которое применяется ко всем нормированным пространствам
  • L пространство - Функция пространства, обобщающие конечномерные пространства с p нормой
  • пространство Соболева - банахово пространство функций с нормой, объединяющее Lᵖ-нормы функции и ее производных
• Проблема искажения
• пространство интерполяции
• Локально выпуклый топологический вектор space - векторное пространство с топологией, определяемой выпуклыми открытыми множествами
• пространство Смита
• Топологическое векторное пространство - векторное пространство с понятием близости

• Банах, Стефан (1932). Теория линейных операций [Теория линейных операций] (PDF). Monografie Matematyczne (на французском языке). 1 . Варшава: Subwencji Funduszu Kultury Narodowej. Zbl 0005.20901. Архивировано из оригинального (PDF) 11 января 2014 года. Проверено 11 июля 2020 г.
• Бозами, Бернард (1985) [1982], Введение в банаховы пространства и их геометрию (второе исправленное издание), Северная Голландия.
• Бурбаки, Николас (1987) [ 1981]. Топологические векторные пространства: главы 1–5 [Sur specific espaces vectoriels topologiques]. Annales de l'Institut Fourier. Éléments de mathématique. 2. Перевод Eggleston, H.G.; Мадан, С. Берлин Нью-Йорк: Springer-Verlag. ISBN 978-3-540-42338-6. OCLC 17499190.
• Карозерс, Нил Л. (2005), Краткий курс теории банахового пространства, Тексты студентов Лондонского математического общества, 64, Кембридж: Cambridge University Press, стр. xii + 184, ISBN 0-521-84283-2.
• Конвей, Джон (1990). Курс функционального анализа. Тексты для выпускников по математике. 96(2-е изд.). Нью-Йорк: Спрингер-Верлаг. ISBN 978-0-387-97245-9. OCLC 21195908.
• Дистел, Джозеф (1984), Последовательности и серии в банаховых пространствах, Graduate Texts in Mathematics, 92, New York: Springer-Verlag, pp. xii + 261, ISBN 0-387-90859-5.
• Dunford, Nelson; Шварц, Якоб Т. с помощью У. Г. Бейда и Р. Г. Бартла (1958), Линейные операторы. I. Общая теория, чистая и прикладная математика, 7, Нью-Йорк: Interscience Publishers, Inc., MR 0117523
• Эдвардс, Роберт Э. (1995). Функциональный анализ: теория и приложения. Нью-Йорк: Dover Publications. ISBN 978-0-486-68143-6. OCLC 30593138.
• Гротендик, Александр (1973). Топологические векторные пространства. Перевод Чалджуба, Орландо. Нью-Йорк: издательство Gordon and Breach Science. ISBN 978-0-677-30020-7. OCLC 886098.
• Ярчоу, Ханс (1981). Локально выпуклые пространства. Штутгарт: B.G. Teubner. ISBN 978-3-519-02224-4. OCLC 8210342.
• Khaleelulla, S.M. (1982). Написано в берлинском Гейдельберге. Контрпримеры в топологических векторных пространствах. Конспект лекций по математике. 936 . Берлин, Нью-Йорк: Springer-Verlag. ISBN 978-3-540-11565-6. OCLC 8588370.
• Кете, Готфрид (1969). Топологические векторные пространства I. Grundlehren der Mathematischen Wissenschaften. 159 . Перевод Гарлинга, Д.Дж.Х. Нью-Йорк: Springer Science Business Media. ISBN 978-3-642-64988-2. MR 0248498. OCLC 840293704.
• Линденштраус, Джорам ; Цафрири, Лиор (1977), Classical Banach Spaces I, Sequence Spaces, Ergebnisse der Mathematik und ihrer Grenzgebiete, 92, Berlin: Springer-Verlag, ISBN 3-540- 08072-4.
• Меггинсон, Роберт Э. (1998), Введение в теорию банахового пространства, Graduate Texts in Mathematics, 183, New York: Springer-Verlag, pp. Xx + 596, ISBN 0-387-98431-3.
• ; (2011). Топологические векторные пространства. Чистая и прикладная математика (Второе изд.). Бока-Ратон, Флорида: CRC Press. ISBN 978-1584888666. OCLC 144216834.
• Робертсон, Алекс П.; Робертсон, Венди Дж. (1980). Топологические векторные пространства.. 53 . Кембридж, Англия: Cambridge University Press. ISBN 978-0-521-29882-7. OCLC 589250.
• Рудин, Вальтер (1991). Функциональный анализ. Международная серия по чистой и прикладной математике. 8 (Второе изд.). Нью-Йорк, Нью-Йорк: McGraw-Hill Science / Engineering / Math. ISBN 978-0-07-054236-5. OCLC 21163277.
• Райан, Раймонд А. (2002), Введение в тензорные произведения банаховых пространств, Монографии Springer по математике, Лондон: Springer-Verlag, стр. Xiv + 225, ISBN 1-85233-437-1.
• Шефер, Гельмут Х. ; (1999). Топологические векторные пространства. GTM. 8(Второе изд.). Нью-Йорк, штат Нью-Йорк: Springer New York Выходные данные Springer. ISBN 978-1-4612-7155-0. OCLC 840278135.
• Swartz, Charles (1992). Введение в функциональный анализ. Нью-Йорк: М. Деккер. ISBN 978-0-8247-8643-4. OCLC 24909067.
• Trèves, François (2006) [1967]. Топологические векторные пространства, распределения и ядра. Минеола, Нью-Йорк: Dover Publications. ISBN 978-0-486-45352-1. OCLC 853623322.
• Вилански, Альберт (2013). Современные методы в топологических векторных пространствах. Минеола, Нью-Йорк: Dover Publications, Inc. ISBN 978-0-486-49353-4. OCLC 849801114.
• Войтащик, Пшемыслав (1991), Пространства Банаха для аналитиков, Кембриджские исследования по высшей математике, 25, Кембридж: Cambridge University Press, стр. Xiv + 382, ISBN 0-521-35618-0.

Викискладе есть материалы, связанные с банаховыми пространствами.

• , Энциклопедия математики, EMS Press, 2001 [1994]
• Weisstein, Eric W. "Banach Space". MathWorld.

.