Компактное пространство

редактировать

Топологические представления о том, что все точки "близки"

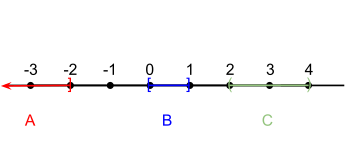
В соответствии с критериями компактности для евклидова пространства, изложенными в Гейне –Теорема Бореля, интервал A = (−∞, −2] не компактен, потому что он не ограничен. Интервал C = (2, 4) не компактен, потому что он не замкнут. Интервал B = [ 0, 1] компактно, потому что оно одновременно замкнуто и ограничено.

В математике, более конкретно в общей топологии, компактность - это свойство, которое обобщает понятие подмножества евклидова пространства, являющегося закрытым (т. е. содержащим все его предельные точки ) и ограниченным (т. е. имеющим все его точки находятся на некотором фиксированном расстоянии друг от друга). Примеры включают закрытый интервал, прямоугольник или конечный набор точек. Это понятие определено для более общего топологические пространства, чем евклидово пространство разными способами.

Одно из таких общих Принцип состоит в том, что топологическое пространство является последовательно компактным, если каждая бесконечная последовательность точек, выбранных из пространства, имеет бесконечную подпоследовательность, которая сходится к некоторой точке пространства. Теорема Больцано – Вейерштрасса утверждает, что подмножество евклидова пространства компактно в этом последовательном смысле тогда и только тогда, когда оно замкнуто и ограничено. Таким образом, если выбрать бесконечное количество точек в замкнутом единичном интервале [0, 1], некоторые из этих точек будут произвольно приближаться к некоторому действительному числу в этом пространстве. Например, некоторые числа в последовательности 1/2, 4/5, 1/3, 5/6, 1/4, 6/7,… накапливаются до 0 (в то время как другие накапливаются до 1). Один и тот же набор точек не может накапливаться ни в одной точке открытого единичного интервала (0, 1); поэтому открытый единичный интервал не является компактным. Само евклидово пространство не компактно, поскольку не ограничено. В частности, последовательность точек 0, 1, 2, 3,…, которая не ограничена, не имеет подпоследовательности, сходящейся к какому-либо действительному числу.

Помимо замкнутых и ограниченных подмножеств евклидова пространства, типичные примеры компактных пространств встречаются в математическом анализе, где свойство компактности некоторых топологических пространств возникает в гипотезах или выводах многих фундаментальных теорем, таких как теорема Больцано – Вейерштрасса, теорема об экстремальных значениях, теорема Арцела – Асколи и теорема существования Пеано. Другой пример - определение распределений, в котором используется пространство гладких функций, которые равны нулю вне некоторого (неуказанного) компактного пространства.

Различные эквивалентные понятия компактности, включая последовательную компактность и компактность предельной точки, могут быть развиты в общих метрических пространствах. Однако в общих топологических пространствах различные понятия компактности не обязательно эквивалентны. Наиболее полезное понятие, которое является стандартным определением безоговорочного термина «компактность», сформулировано в терминах существования конечных семейств открытых множеств, которые «покрывают » пространство в смысле что каждая точка пространства лежит в некотором множестве, содержащемся в семействе. Это более тонкое понятие, введенное Павлом Александровым и Павлом Урысоном в 1929 году, демонстрирует компактные пространства как обобщения конечных множеств. В пространствах, которые компактны в этом смысле, часто можно объединить информацию, которая хранится локально, то есть в окрестности каждой точки, в соответствующие утверждения, которые выполняются во всем пространстве, и многие теоремы являются этого персонажа.

Термин компактный набор иногда используется как синоним компактного пространства, но часто также относится к компактному подпространству топологического пространства.

Содержание

1 Историческое развитие
2 Основные примеры
3 Определения
- 3.1 Определение открытой крышки
- 3.2 Компактность подмножеств
- 3.3 Эквивалентные определения
  - 3.3.1 Евклидово пространство
  - 3.3.2 Метрические пространства
  - 3.3.3 Характеризация непрерывными функциями
  - 3.3.4 Гиперреальное определение
4 Достаточные условия
5 Свойства компактных пространств
- 5.1 Функции и компактные пространства
- 5.2 Компактификации
- 5.3 Упорядоченные компактные пространства
6 Примеры
- 6.1 Алгебраические примеры
7 См. Также
8 Примечания
9 Ссылки
10 Библиография
11 Внешние ссылки

Историческое развитие

В 19 веке были поняты несколько разрозненных математических свойств, которые позже будут рассматриваться как следствия компактности. С одной стороны, Бернар Больцано (1817) знал, что любая ограниченная последовательность точек (например, на прямой или плоскости) имеет подпоследовательность, которая в конечном итоге должна быть произвольно близкой в некоторую другую точку, называемую предельной точкой. Доказательство Больцано опиралось на метод деления пополам : последовательность была помещена в интервал, который затем был разделен на две равные части, и была выбрана часть, содержащая бесконечно много членов последовательности. Затем процесс можно было бы повторить, разделив полученный меньший интервал на все меньшие и меньшие части - до тех пор, пока он не приблизится к желаемой предельной точке. Полное значение теоремы Больцано и метода ее доказательства проявится лишь спустя почти 50 лет, когда она была заново открыта Карлом Вейерштрассом.

. В 1880-х годах стало ясно, что результаты аналогичны к теореме Больцано – Вейерштрасса можно было бы сформулировать для пространств функций, а не только для чисел или геометрических точек. Идея рассматривать функции как точки обобщенного пространства восходит к исследованиям Джулио Асколи и Чезаре Арзела. Кульминация их исследований, теорема Арцела – Асколи, явилась обобщением теоремы Больцано – Вейерштрасса на семейства непрерывных функций, точный вывод из которого состоял в том, что возможно извлечь равномерно сходящуюся последовательность функций из подходящего семейства функций. Тогда равномерный предел этой последовательности играл в точности ту же роль, что и «предельная точка» Больцано. К началу двадцатого века результаты, аналогичные результатам Арцела и Асколи, начали накапливаться в области интегральных уравнений, как исследовали Дэвид Гильберт и Эрхард Шмидт. Для определенного класса функций Грина, возникающих из решений интегральных уравнений, Шмидт показал, что свойство, аналогичное теореме Арцела – Асколи, имеет место в смысле сходимости в среднем - или сходимости в что позже будет названо гильбертовым пространством. В конечном итоге это привело к понятию компактного оператора как ответвлению общего понятия компактного пространства. Это был Морис Фреше, который в 1906 выявил сущность свойства Больцано-Вейерштрасса и ввел термин компактность для обозначения этого общего явления (он использовал этот термин уже в своей Статья 1904 г., которая привела к знаменитой диссертации 1906 г.).

Однако совершенно другое понятие компактности в целом также медленно появилось в конце XIX века из исследования континуума, которое считалось фундаментальным для строгой формулировки анализа. В 1870 году Эдуард Гейне показал, что непрерывная функция, определенная на замкнутом и ограниченном интервале, на самом деле равномерно непрерывна. В ходе доказательства он использовал лемму о том, что из любого счетного покрытия интервала меньшими открытыми интервалами можно выбрать конечное число из них, которые также покрывают его. Значение этой леммы было признано Эмилем Борелем (1895), и она была обобщена на произвольные наборы интервалов (1895) и Анри Лебегом (1904). Теорема Гейне – Бореля, как теперь известен результат, является еще одним особым свойством, которым обладают замкнутые и ограниченные множества действительных чисел.

Это свойство было важным, поскольку оно позволяло переход от локальной информации о наборе (такой как непрерывность функции) к глобальной информации о наборе (такой как равномерная непрерывность функция). Это мнение было выражено Лебегом (1904), который также использовал его при разработке интеграла, теперь носящего его имя. В конце концов, русская школа точечной топологии под руководством Павла Александрова и Павла Урысона сформулировала компактность Гейне-Бореля таким образом, чтобы применительно к современному понятию топологического пространства. Александров и Урысон (1929) показали, что более ранняя версия компактности, обусловленная Фреше, теперь называемая (относительной) последовательной компактностью, при соответствующих условиях, вытекающих из версии компактности, сформулированной в условия существования конечных субпокрытий. Именно это понятие компактности стало доминирующим, потому что это было не только более сильным свойством, но и его можно было сформулировать в более общем контексте с минимумом дополнительных технических средств, поскольку оно опиралось только на структуру открытых множеств. в пространстве.

Основные примеры

Любое конечное пространство тривиально компактно. Нетривиальным примером компактного пространства является (замкнутый) единичный интервал [0,1] действительных чисел. Если выбрать бесконечное количество различных точек в единичном интервале, тогда в этом интервале должна быть некоторая точка накопления. Например, члены с нечетными номерами последовательности 1, 1/2, 1/3, 3/4, 1/5, 5/6, 1/7, 7/8,... становятся сколь угодно близкими к 0, в то время как четные становятся произвольно близкими к 1. Данная последовательность примеров показывает важность включения граничных точек интервала, поскольку предельные точки должны находиться в самом пространстве - открытый (или полуоткрытый) интервал действительных чисел не является компактным. Также очень важно, чтобы интервал был ограничен, поскольку в интервале [0, ∞) можно было выбрать последовательность точек 0, 1, 2, 3,..., из которых не было под- последовательность в конечном итоге становится произвольно близкой к любому заданному действительному числу.

В двух измерениях замкнутые диски компактны, поскольку для любого бесконечного числа точек, взятых с диска, некоторое подмножество этих точек должно быть произвольно близко либо к точке на диске, либо до точки на границе. Однако открытый диск не является компактным, потому что последовательность точек может стремиться к границе, не приближаясь произвольно к какой-либо точке внутри. Точно так же сферы компактны, но сфера, в которой отсутствует точка, - нет, поскольку последовательность точек все еще может стремиться к отсутствующей точке, тем самым не приближаясь произвольно к любой точке в пространстве. Линии и плоскости не являются компактными, поскольку можно взять набор равноотстоящих точек в любом заданном направлении, не приближаясь к какой-либо точке.

Определения

В зависимости от уровня общности могут применяться различные определения компактности. Подмножество евклидова пространства, в частности, называется компактным, если оно закрытое и ограниченное. Это означает, по теореме Больцано – Вейерштрасса, что любая бесконечная последовательность из множества имеет подпоследовательность, которая сходится к точке в множестве. Различные эквивалентные понятия компактности, такие как последовательная компактность и компактность предельной точки, могут быть развиты в общем метрических пространств.

Напротив, различные понятия компактности не являются в целом эквивалентны топологическим пространствам, а наиболее полезное понятие компактности - первоначально называвшееся бикомпактностью - определяется с помощью покрытий, состоящих из открытых множеств (см. определение открытого покрытия ниже). То, что эта форма компактности выполняется для замкнутых и ограниченных подмножеств евклидова пространства, известно как теорема Гейне – Бореля. Компактность, определенная таким образом, часто позволяет взять информацию, которая известна локально - в окрестности каждой точки пространства - и расширить ее до информации, которая хранится глобально. во всем пространстве. Примером этого явления является теорема Дирихле, к которой она была первоначально применена Гейне, о том, что непрерывная функция на компактном интервале равномерно непрерывна ; здесь непрерывность - это локальное свойство функции, а равномерная непрерывность - соответствующее глобальное свойство.

Определение открытого покрытия

Формально, топологическое пространство X называется компактным, если каждое из его открытых покрытий имеет конечное прикрытие. То есть X компактно, если для каждого набора C открытых подмножеств X такого, что

X = ⋃ x ∈ C x {\ displaystyle X = \ bigcup _ {x \ in C} x}

X=\bigcup _{x\in C}x

существует конечное подмножество F в C такое, что

X = ⋃ x ∈ F x. {\ displaystyle X = \ bigcup _ {x \ in F} x.}

X=\bigcup _{x\in F}x.

Некоторые разделы математики, такие как алгебраическая геометрия, обычно находящиеся под влиянием французской школы Бурбаки, используйте термин квазикомпактный для общего понятия и оставьте термин компактный для топологических пространств, которые одновременно хаусдорфовы и квазикомпактны. Компактное множество иногда называют компактом множественного числа.

Компактность подмножеств

Подмножество K топологического пространства X называется компактным, если оно компактно как подпространство (в топологии подпространств ). То есть K компактно, если для любого произвольного набора C открытых подмножеств X такого, что

K ⊆ ⋃ c ∈ C c {\ displaystyle K \ substeq \ bigcup _ {c \ in C} c}

K\subseteq \bigcup _{c\in C}c

существует представляет собой конечное подмножество F в C такое, что

K ⊆ ⋃ c ∈ F c {\ displaystyle K \ substeq \ bigcup _ {c \ in F} c}

K\subseteq \bigcup _{c\in F}c

Компактность - это "топологический " свойство. То есть, если $K ⊂ Z ⊂ Y {\ displaystyle K \ subset Z \ subset Y}$ $K\subset Z\subset Y$ , с подмножеством Z, снабженным топологией подпространства, то K компактно в Z тогда и только тогда, когда K компактно в Y.

Эквивалентные определения

Следующие эквивалентны:

Топологическое пространство X компактно.
Каждая открытая крышка из X имеет конечное подпокрытие .
X имеет такую подбазу, что каждое покрытие пространства членами подбазы имеет конечное подпокрытие (теорема Александера о подбазе )
Любое совокупность замкнутых подмножеств X со свойством конечного пересечения имеет непустое пересечение.
Каждая сеть на X имеет сходящуюся подсеть (см. статью о сетях для доказательства).
Каждый фильтр на X имеет сходящееся уточнение.
Каждая сеть на X имеет точку кластера.
Каждый фильтр на X имеет точку кластера.
Каждый ультрафильтр на X сходится по крайней мере к одной точке.
Каждое бесконечное подмножество X имеет полное накопление точка.

Евклидово пространство

Для любого подмножества A из евклидова пространства ℝ, A компактно тогда и только тогда, когда оно закрыто и ограниченный ; это теорема Гейне – Бореля.

Поскольку евклидово пространство является метрическим пространством, условия следующего подраздела также применимы ко всем его подмножествам. Из всех эквивалентных условий на практике проще всего проверить, что подмножество замкнуто и ограничено, например, для замкнутого интервала или замкнутого n-шара.

Метрические пространства

Для любого метрического пространства (X, d) следующие условия эквивалентны (при условии счетного выбора ):

(X, d) компактно.
(X, d) является полным и полностью ограниченным (это также эквивалентно компактности для равномерных пространств ).
(X, d) является последовательно компактным; то есть каждая последовательность в X имеет сходящуюся подпоследовательность, предел которой находится в X (это также эквивалентно компактности для first-countable равномерных пространств ).
(X, d) компактно по предельной точке (также называемое счетно компактным); то есть каждое бесконечное подмножество X имеет по крайней мере одну предельную точку в X.
(X, d) является образом непрерывной функции из канторова множества.

Компактное метрическое пространство (X, d) также удовлетворяет следующим свойствам:

Числовая лемма Лебега : для любого открытого покрытия X, существует такое число δ>0, что каждое подмножество X диаметра < δ is contained in some member of the cover.
(X, d) является подсчитываемым по секундам, отделимым и Линделёфом - эти три условия эквивалентны для метрических пространств. Обратное неверно; например, счетное дискретное пространство удовлетворяет этим трем условиям, но не является компактным.
X замкнуто и ограничено (как подмножество любого метрического пространства, ограниченная метрика которого равна d). Обратное может быть неверным для неевклидова пространства; например вещественная линия, снабженная дискретной метрикой, замкнута и ограничена, но не компактна, так как совокупность всех синглтонов пространства является открытой крышкой, которая не допускает конечное подпокрытие. Оно полное, но не полностью ограничено.

Характеризация непрерывными функциями

Пусть X - топологическое пространство, а C (X) - кольцо вещественных непрерывных функций на X. Для каждого p ∈ X оценочное отображение $ev p: C (X) → R {\ displaystyle \ operatorname {ev} _ {p} \ двоеточие C (X) \ to \ mathbf {R}}$ $\operatorname {ev} _{p}\colon C(X)\to \mathbf {R}$ задано ev p (f) = f (p) - гомоморфизм колец. ядро ev p является максимальным идеалом, поскольку поле вычетов C (X) / ker ev p - это поле действительных чисел, согласно первой теореме об изоморфизме . Топологическое пространство X является псевдокомпактным тогда и только тогда, когда каждый максимальный идеал в C (X) имеет поле вычетов действительных чисел. Для полностью регулярных пространств это эквивалентно тому, что каждый максимальный идеал является ядром оценочного гомоморфизма. Однако есть псевдокомпактные пространства, которые не являются компактными.

В общем, для непсевдокомпактных пространств всегда существуют максимальные идеалы m в C (X) такие, что поле вычетов C (X) / m является (неархимедовым ) гиперреальное поле. Структура нестандартного анализа допускает следующую альтернативную характеристику компактности: топологическое пространство X компактно тогда и только тогда, когда каждая точка x естественного расширения * X бесконечно близка в точку x 0 X (точнее, x содержится в монаде x 0).

Гиперреальное определение

Пространство X компактно, если его гиперреальное расширение * X (построенное, например, с помощью сверхстепенной конструкции ) имеет свойство, что каждая точка из * X бесконечно близка к некоторой точке из X⊂ * X. Например, открытый вещественный интервал X = (0, 1) не является компактным, потому что его гиперреальное расширение * (0,1) содержит бесконечно малые значения, бесконечно близкие к 0, который не является точкой X.

Достаточные условия

Замкнутое подмножество компакта компактно.
Конечное объединение компактов компактно.
A непрерывный образ компактного пространства есть компактный.
Пересечение любого набора компактных подмножеств хаусдорфового пространства компактно (и замкнуто);
- Если X не хаусдорфово, то пересечение двух компактных подмножеств может не быть компактным (см., Например, сноску).
произведение любого набора компактных пространств компактно. (Это теорема Тихонова, которая эквивалентна аксиоме выбора .)
В метризуемом пространстве подмножество компактно тогда и только тогда, когда оно последовательно компактное (при условии счетного выбора )
Конечное множество, снабженное любой топологией, компактно.

Свойства компактных пространств

Компактное подмножество хаусдорфова пространства X является закрыто.
- Если X не хаусдорфово, то компактное подмножество X может не быть замкнутым подмножеством X (см., например, сноску).
- Если X не хаусдорфово, то закрытие компактный набор может не быть компактным (см., например, сноску).
В любом топологическом векторном пространстве (TVS) компактное подмножество является полным. Однако каждое не- Хаусдорфова TVS содержит компактные (и, следовательно, полные) подмножества, которые не являются замкнутыми.
Если A и B - непересекающиеся компактные подмножества хаусдорфового пространства X, то существуют непересекающиеся открытые множества U и V в X такие, что A ⊆ U и B ⊆ V.
Непрерывная биекция из компактного sp ace в хаусдорфово пространство является гомеоморфизмом.
Компактное хаусдорфово пространство нормально и регулярно.
Если пространство X компактно и хаусдорфово, то более тонкая топология на X не является компактная и не более грубая топология на X хаусдорфова.
Если подмножество метрического пространства (X, d) компактно, то оно d-ограничено.

Функции и компактные пространства

Так как непрерывный образ компактного пространства компактен, теорема об экстремальном значении : непрерывная вещественнозначная функция на непустом компактном пространстве ограничена сверху и достигает своей верхней грани. (В более общем смысле, это верно для полунепрерывной сверху функции.) Как своего рода обратное к приведенным выше утверждениям, прообраз компактного пространства под правильным отображением является компактным.

Компактификации

Каждое топологическое пространство X является открытым плотным подпространством компактного пространства, имеющего не более чем на одну точку больше, чем X, на одну точку Александрова. компактификация. По той же конструкции любое локально компактное хаусдорфово пространство X является открытым плотным подпространством компактного хаусдорфова пространства, имеющего не более одной точки больше, чем X.

Упорядоченные компактные пространства

Непустое компактное подмножество вещественных чисел имеет наибольший элемент и наименьший элемент.

Пусть X будет просто упорядоченным набором, наделенным топологией порядка . Тогда X является компактным тогда и только тогда, когда X является полной решеткой (т.е. все подмножества имеют верхнюю и нижнюю границу).

Примеры

Любое конечное топологическое пространство, включая пустой набор, является компактным. В более общем смысле, любое пространство с конечной топологией (только конечное число открытых множеств) компактно; это включает, в частности, тривиальную топологию.
Любое пространство, несущее конфинитную топологию, компактно.
Любое локально компактное пространство Хаусдорфа можно превратить в компактное пространство, добавив к нему одну точку с помощью одноточечной компактификации Александрова. Одноточечная компактификация гомеоморфна окружности S ; одноточечная компактификация гомеоморфна сфере S . Используя одноточечную компактификацию, можно также легко построить компактные пространства, не являющиеся хаусдорфовыми, начав с нехаусдорфова пространства.
Топология правого порядка или левого порядка топология на любом ограниченном вполне упорядоченном множестве компактна. В частности, пространство Серпинского компактно.
Никакое дискретное пространство с бесконечным числом точек не компактно. Совокупность всех синглтонов пространства представляет собой открытое покрытие, не допускающее конечного подпокрытия. Конечные дискретные пространства компактны.
В ℝ, несущем топологию нижнего предела, никакое несчетное множество не является компактным.
В сосчетной топологии на бесчисленное множество, никакое бесконечное множество не бывает компактным. Как и в предыдущем примере, пространство в целом не локально компактно, но по-прежнему является Линделёфом.
. Замкнутый единичный интервал [0,1] компактный. Это следует из теоремы Гейне – Бореля. Открытый интервал (0,1) не является компактным: открытая крышка $(1 n, 1 - 1 n) {\ displaystyle \ left ({\ frac {1} {n}}, 1 - {\ frac {1} {n}} \ right)}$ $\left({\frac {1}{n}},1-{\frac {1}{n}}\right)$ для n = 3, 4,… не имеет конечного подпокрытия. Аналогично, множество рациональных чисел на отрезке [0,1] не является компактным: множества рациональных чисел на отрезках $[0, 1 π - 1 n] и [1 π + 1 n, 1] {\ displaystyle \ left [0, {\ frac {1} {\ pi}} - {\ frac {1} {n}} \ right] \ {\ text {и}} \ \ left [{\ frac {1} {\ pi}} + {\ frac {1} {n}}, 1 \ right]}$ $\left[0,{\frac {1}{\pi }}-{\frac {1}{n}}\right]\ {\text{and}}\ \left[{\frac {1}{\pi }}+{\frac {1}{n}},1\right]$ покрывают все рациональные числа в [0, 1] для n = 4, 5,... но это покрытие не имеет конечного подпокрытия. Здесь множества открыты в топологии подпространства, даже если они не открыты как подмножества.
Множество ℝ всех действительных чисел не компактно, так как существует покрытие открытых интервалов, не имеющее конечное подпокрытие. Например, интервалы (n − 1, n + 1), где n принимает все целые значения в Z, покрывают ℝ, но нет конечного подпокрытия.
С другой стороны, строка с расширенными действительными числами, несущая аналогичную топологию, компактна; обратите внимание, что описанная выше крышка никогда не достигнет бесконечно удаленных точек. Фактически, набор имеет гомеоморфизм в [-1,1] отображения каждой бесконечности в соответствующую единицу и каждое действительное число в его знак, умноженный на уникальное число в положительной части интервала, что приводит к его абсолютное значение при делении на единицу минус само по себе, и поскольку гомеоморфизмы сохраняют покрытия, можно вывести свойство Гейне-Бореля.
Для каждого натурального числа n n-сфера компактный. Снова из теоремы Гейне – Бореля, замкнутый единичный шар любого конечномерного нормированного векторного пространства компактен. Это неверно для бесконечных измерений; фактически, нормированное векторное пространство конечномерно тогда и только тогда, когда его замкнутый единичный шар компактен.
С другой стороны, замкнутый единичный шар двойственного к нормированному пространству компактна для слабой * топологии. (Теорема Алаоглу )
Канторовское множество компактно. Фактически, каждое компактное метрическое пространство является непрерывным образом Канторовского множества.
Рассмотрим множество K всех функцийf : ℝ → [0,1] от прямой до замкнутого единичного интервала и определите топологию на K так, чтобы последовательность ${fn} {\ displaystyle \ {f_ {n} \}}$ $\{f_{n}\}$ в K сходится к f ∈ K тогда и только тогда, когда ${fn (x)} {\ displaystyle \ {f_ {n} (x) \}}$ $\{f_{n}(x)\}$ сходится к f (x) для всех действительных чисел x. Такая топология только одна; она называется топологией точечной сходимости или топологией произведения. Тогда K - компактное топологическое пространство; это следует из Теорема Тихонова.
Рассмотрим множество K всех функций f: [0,1] → [0,1], удовлетворяющих условию Липшица | f (x) - f (y) | ≤ | x - y | для всех x, y ∈ [0,1]. Рассмотрим на K метрику, индуцированную равномерным расстоянием $d (f, g) = sup x ∈ [0, 1 ] | е (х) - г (х) |, {\ displaystyle d (f, g) = \ sup _ {x \ in [0,1]} | f (x) -g (x) |.}$ $d(f,g)=\sup _{x\in [0,1]}|f(x)-g(x)|.$ Тогда по теореме Арзела – Асколи пространство K компактно.
Спектр любого линейного ограниченного оператора в банаховом пространстве является непустым компактным подмножеством комплексных чисел ℂ. Наоборот, любое компактное подмножество возникает таким образом как спектр некоторого ограниченного линейного оператора. Например, диагональный оператор в гильбертовом пространстве $ℓ 2 {\ displaystyle \ ell ^ {2}}$ $\ell ^{2}$ может иметь любое компактное непустое подмножество ℂ в качестве спектра.

Алгебраические примеры

Компактные группы, такие как ортогональная группа, являются компактными, в то время как группы, такие как общая линейная группа, нет.
Поскольку p-адическая целые числа гомеоморфны множеству Кантора, они образуют компактное множество.
Спектр любого коммутативного кольца с Топология Зариского (то есть множество всех простых идеалов) компактна, но никогда не Хаусдорфа (кроме тривиальных случаев). В алгебраической геометрии такие топологические пространства являются примерами квазикомпактных схем, «квази», относящихся к нехаусдорфовой природе топологии.
Компактность, факт, который является частью из теоремы Стоуна о представлении. Каменные пространства, компактные полностью несвязные хаусдорфовы пространства образуют абстрактную основу, в которой изучаются эти спектры. Такие пространства также полезны при изучении проконечных групп.
структурное пространство коммутативной унитальной банаховой алгебры является компактным хаусдорфовым пространством.
куб Гильберта компактен, что опять же является следствием теоремы Тихонова.
A проконечная группа (например, группа Галуа ) компактна.

См. Также

Примечания

Ссылки

Библиография

Александров, Павел ; Урысон, Павел (1929), "Mémoire sur les espaces topologiques compacts", Koninklijke Nederlandse Akademie van Wetenschappen Te Amsterdam, Труды Секции математических наук, 14.
Архангельский А.В.; Федорчук, В. (1990), «Основные понятия и конструкции общей топологии», Архангельский, А.В.; Понтрягин, Л. (ред.), Общая топология I, Энциклопедия математических наук, 17, Springer, ISBN 978-0-387-18178-3.
Архангельский, AV (2001) [1994], Encyclopedia of Mathematics, EMS Press.
Bolzano, Bernard (1817), Rein analytischer Beweis des Lehrsatzes, dass zwischen je zwey Werthen, die ein entgegengesetzes Resultat gewähren, wenigstens eine reele Wurzel der Gleichung liege, Wilhelm Engelmann (Чисто аналитическое доказательство теоремы о том, что между любыми двумя значениями, дающими результаты с противоположным знаком, лежит по крайней мере одно действительное корень уравнения).
Борель, Эмиль (1895), "Sur quelques points de la théorie des fonctions", Annales Scientifiques de l'École Normale Supérieure, 3, 12 : 9–55, doi : 10.24033 / asens.406, JFM 26.0429.03
Бойер, Карл Б. (1959), История исчисления и его концептуальное развитие, Нью-Йорк: Dover Publications, MR 0124178.
Бойер, Карл Бенджамин ; Merzbach, Uta C (1991), История математики (2-е изд.), John Wiley Sons, Inc., ISBN 978- 0-471-54397-8.
Arzelà, Cesare (1895), "Sulle funzioni di linee", Mem. Accad. Sci. Ist. Болонья Cl. Sci. Fis. Матем., 5 (5): 55–74.
Arzelà, Cesare (1882–1883), «Un'osservazione intorno all serie di funzioni», Rend. Dell 'Accad. R. Delle Sci. dell'Istituto di Bologna: 142–159.
Ascoli, G. (1883–1884), «Le curve limiti di una varietà data di curve», Атти делла Р. Аккад. Dei Lincei Memorie della Cl. Sci. Fis. Мат. Nat., 18 (3): 521–586.
Fréchet, Maurice (1906), «Sur quelques points du Calcul fonctionnel», Rendiconti del Circolo Matematico di Palermo, 22(1): 1–72, doi : 10.1007 / BF03018603, hdl : 10338.dmlcz / 100655, S2CID 123251660.
Гиллман, Леонард; Jerison, Meyer (1976), Rings of continuous functions, Springer-Verlag.
Kelley, John (1955), General topology, Graduate Texts in Mathematics, 27, Springer-Verlag.
Kline, Morris (1972), Mathematical thought from ancient to modern times (3rd ed.), Oxford University Press (published 1990), ISBN 978-0-19-506136-9.
Lebesgue, Henri (1904), Leçons sur l'intégration et la recherche des fonctions primitives, Gauthier-Villars.
Robinson, Abraham (1996), Non-standard analysis, Princeton University Press, ISBN 978-0-691-04490-3, MR 0205854.
Scarborough, C.T.; Stone, A.H. (1966), "Products of nearly compact spaces" (PDF), Transactions of the American Mathematical Society, Transactions of the American Mathematical Society, Vol. 124, No. 1, 124(1): 131–147, doi :10.2307/1994440, JSTOR 1994440.
Steen, Lynn Arthur ; Seebach, J. Arthur Jr. (1995) [1978], Counterexamples in Topology (Dover Publications reprint of 1978 ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-486-68735-3, MR 0507446
Willard, Stephen (1970), General Topology, Dover publications, ISBN 0-486-43479-6

External links

Countably compact at PlanetMath.org.
Sundström, Manya Raman (2010). "A pedagogical history of compactness". arXiv :1006.4131v1 [math.HO ].Cite has empty unknown parameter: |version=()

This article incorporates material from Examples of compact spaces on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.