Набор Кантора

Набор точек на отрезке линии

В математике, Кантор set - это набор точек, лежащих на одном отрезке линии, который имеет ряд замечательных и глубоких свойств. Он был открыт в 1874 году Генри Джоном Стивеном Смитом и представлен немецким математиком Георгом Кантором в 1883 году.

Рассмотрев этот набор, Кантор и другие помогли заложить основы современной точечной топологии. Хотя сам Кантор определен набор в общем, абстрактном смысле, наиболее распространенной современной конструкцией является троичный набор Кантора, построенный путем стандартной трети линейного сегмента и последующего повторения процесса оставшимися более короткими сегментами.. Сам Кантор представил троичную конструкцию лишь в качестве примера более общего множественного множества, нигде не плотно.

Увеличить масштаб множества Кантора. Каждая точка в наборе представлена ​​здесь вертикальной линией.

• 1 Построение и формула троичного набора
• 2 Состав
• 3 Свойства
  • 3.1 Мощность
  • 3.2 Самоподобие
  • 3.3 Закон сохранение
  • 3.4 Топологические и аналитические свойства
  • 3.5 Мера и вероятность
  • 3.6 Числа Кантора
  • 3.7 Теория дескриптивных множеств
• 4 варианта
  • 4.1 Множество Смита - Вольтерра - Кантора
  • 4.2 Стохастический набор Кантора
  • 4.3 Канторовская пыль
• 5 Исторические заметки
• 6 См. Также
• 7 Примечания
• 8 Ссылки
• 9 Внешние ссылки

троичный набор Кантора $C\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{C\}\}\}$создается путем итеративного удаления открытый средней трети из набора отрезки линии. Первый начинается с удаления открытой средней трети (1/3, 2/3) из интервала [0, 1], оставляя два отрезка линии: [0, 1/3] ∪ [2/3, 1]. Затем открылась средняя часть из этих оставшихся сегментов: [0, 1/9] ∪ [2/9, 1/3] ∪ [2/3, 7/9] ∪ [8/9, 1 ]. Этот процесс продолжается до бесконечности, где n-й набор равен

$C\; n\; =\; C\; n\; -\; 1\; 3\; \cup \; (2\; 3\; +\; C\; n\; -\; 1\; 3)\; для\; n\; \ge \; 1,\; а\; C\; 0\; =\; [\; 0,\; 1].\; \{\backslash \; displaystyle\; C\_\; \{n\}\; =\; \{\backslash \; frac\; \{C\_\; \{n-1\}\}\; \{3\}\}\; \backslash \; cup\; \backslash \; left\; (\{\backslash \; frac\; \{2\}\; \{3\}\}\; +\; \{\backslash \; frac\; \{C\_\; \{n-1\}\}))\; \{3\}\}\; \backslash \; right)\; \{\backslash \; text\; \{for\}\}\; n\; \backslash \; geq\; 1,\; \{\backslash \; text\; \{and\}\}\; C\_\; \{0\}\; =\; [0,1].\}$

Тернарный набор Кантора содержит все точки в интервале [0, 1], которые не удаляются ни на одном этапе этого бесконечного процесса:

$C:\; =\; \bigcap \; n\; =\; 1\; \infty \; C\; n.\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{C\}\}:\; =\; \backslash \; bigcap\; \_\; \{n\; =\; 1\}\; ^\; \{\backslash \; infty\}\; C\_\; \{n\}.\}$

Первые шесть шагов этого процесса показаны ниже.

Используя идею самоподобных преобразований, $TL\; (x)\; =\; x\; /\; 3,\; TR\; (x)\; =\; (2\; +\; x)\; /\; 3\; \{\backslash \; displaystyle\; T\_\; \{L\}\; (x)\; =\; x\; /\; 3,\; T\_\; \{R\; \}\; (x)\; =\; (2\; +\; x)\; /\; 3\}$и $C\; n\; =\; TL\; (C\; n\; -\; 1)\; \cup \; TR\; (C\; n\; -\; 1),\; \{\backslash \; displaystyle\; C\_\; \{n\}\; =\; T\_\; \{L\}\; (C\_\; \{n-1\})\; \backslash \; cup\; T\_\; \{R\}\; (C\_\; \{n-1\}),\}$явные закрытые формулы для набора Кантора:

$С\; знак\; равно\; [0,\; 1]\; \setminus \; \bigcup \; N\; знак\; равно\; 0\; \infty \; \bigcup \; К\; знак\; равно\; 0\; 3\; N\; -\; 1\; (3\; К\; +\; 1\; 3\; N\; +\; 1,\; 3\; К\; +\; 2\; 3\; N\; +\; 1),\; \{\backslash \; Displaystyle\; \{\backslash \; mathcal\; \{C\}\}\; =\; [\; 0,1]\; \backslash \; smallsetminus\; \backslash \; bigcup\; \_\; \{n\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \backslash \; bigcup\; \_\; \{k\; =\; 0\}\; ^\; \{3\; ^\; \{n\}\; -1\}\; \backslash \; left\; (\{\backslash \; frac\; \{3k\; +\; 1\}\; \{3\; ^\; \{n\; +\; 1\}\}\},\; \{\backslash \; frac\; \{3k\; +\; 2\}\; \{3\; ^\; \{n\; +\; 1\}\}\}\; \backslash \; right),\}$

где каждая средняя треть удаляется как открытый интервал $(3\; к\; +\; 1\; 3\; n\; +\; 1,\; 3\; к\; +\; 2\; 3\; n\; +\; 1)\; \{\backslash \; displaystyle\; \backslash \; textstyle\; \backslash \; left\; (\{\backslash \; frac\; \{3k\; +\; 1\}\; \{3\; ^\; \{n\; +\; 1\}\}\},\; \{\backslash \; frac\; \{3k\; +\; 2\})\; \{3\; ^\; \{n\; +\; 1\}\}\}\; \backslash \; right)\}$из закрытого интервала $[3\; k\; +\; 0\; 3\; n\; +\; 1,\; 3\; k\; +\; 3\; 3\; n\; +\; 1]\; =\; [к\; +\; 0\; 3\; N,\; К\; +\; 1\; 3\; N]\; \{\backslash \; displaystyle\; \backslash \; textstyle\; \backslash \; left\; [\{\backslash \; frac\; \{\; 3k\; +\; 0\}\; \{3\; ^\; \{n\; +\; 1\}\}\},\; \{\backslash \; frac\; \{3k\; +\; 3\}\; \{3\; ^\; \{n\; +\; 1\}\}\}\; \backslash \; right]\; =\; \backslash \; left\; [\{\backslash \; frac\; \{k\; +\; 0\}\; \{3\; ^\; \{n\}\}\},\; \{\backslash \; frac\; \{k\; +\; 1\}\; \{3\; ^\; \{n\}\}\}\; \backslash \; right]\}$вокруг него, или

$C\; =\; \bigcap \; n\; =\; 1\; \infty \; \bigcup \; k\; =\; 0\; 3\; n\; -\; 1\; -\; 1\; ([3\; k\; +\; 0\; 3\; n,\; 3\; k\; +\; 1\; 3\; n]\; \cup \; [3\; k\; +\; 2\; 3\; n,\; 3\; k\; +\; 3\; 3\; n]),\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{C\}\; \}\; =\; \backslash \; bigcap\; \_\; \{n\; =\; 1\}\; ^\; \{\backslash \; infty\}\; \backslash \; bigcup\; \_\; \{k\; =\; 0\}\; ^\; \{3\; ^\; \{n-1\}\; -1\}\; \backslash \; left\; (\backslash \; left\; [\{\backslash \; frac\; \{3k\; +\; 0\}\; \{\; 3\; ^\; \{n\}\}\},\; \{\backslash \; frac\; \{3k\; +1\}\; \{3\; ^\; \{n\}\}\}\; \backslash \; right]\; \backslash \; cup\; \backslash \; left\; [\{\backslash \; frac\; \{3k\; +\; 2\}\; \{3\; ^\; \{n\}\}\},\; \{\; \backslash \; frac\; \{3k\; +\; 3\}\; \{3\; ^\; \{n\}]\}\}\; \backslash \; right]\; \backslash \; right),\}$

где средняя треть $(3\; k\; +\; 1\; 3\; n,\; 3\; k\; +\; 2\; 3\; n)\; \{\backslash \; displaystyle\; \backslash \; textstyle\; \backslash \; left\; (\{\backslash \; frac\; \{3k\; +\; 1\}\; \{3\; ^\; \{n\}\}\},\; \{\backslash \; frac\; \{3k\; +\; 2\}\; \{3\; ^\; \{n\}\}\}\; \backslash \; right)\}$предыдущий закрытого интервала $[k\; +\; 0\; 3\; n\; -\; 1,\; к\; +\; 1\; 3\; n\; -\; 1]\; =\; [3\; k\; +\; 0\; 3\; n,\; 3\; k\; +\; 3\; 3\; n]\; \{\backslash \; displaystyle\; \backslash \; textstyle\; \backslash \; left\; [\{\backslash \; frac\; \{\; k\; +\; 0\}\; \{3\; ^\; \{n-1\}\}\},\; \{\backslash \; frac\; \{k\; +\; 1\}\; \{3\; ^\; \{n-1\}\}\}\; \backslash \; right]\; =\; \backslash \; left\; [\{\backslash \; frac\; \{3k\; +\; 0\}\; \{3\; ^\; \{n\}\}\},\; \{\backslash \; frac\; \{3k\; +\; 3\}\; \{3\; ^\; \{n\}\}\}\; \backslash \; right]\}$у даляется пересечением с $[3\; k\; +\; 0\; 3\; n,\; 3\; k\; +\; 1\; 3\; n]\; \cup \; [3\; k\; +\; 2\; 3\; n,\; 3\; k\; +\; 3\; 3\; n].\; \{\backslash \; displaystyle\; \backslash \; textstyle\; \backslash \; left\; [\{\backslash \; frac\; \{3k\; +\; 0\}\; \{3\; ^\; \{n\}\}\},\; \{\backslash \; frac\; \{3k\; +\; 1\}\; \{3\; ^\; \{n\}\}\}\; \backslash \; right]\; \backslash \; cup\; \backslash \; left\; [\{\; \backslash \; frac\; \{3k\; +\; 2\}\; \{3\; ^\; \{n\}\}\},\; \{\backslash \; frac\; \{3k\; +\; 3\}\; \{3\; ^\; \{n\}\}\}\; \backslash \; right].\}$

Этот процесс среднего третей является простым правилом примера конечного подразделения. Тройной набор Кантора является примером фрактальной строки.

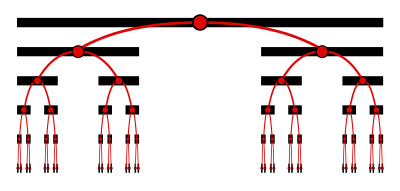
В арифметических терминах набор Кантора состоит из всех действующих чисел единичного интервала $[0,\; 1]\; \{\backslash \; displaystyle\; [0,1]\}$, которые не требуют цифры 1, чтобы быть выраженными как троичная (основание 3) дробь. Как показано на приведенной выше диаграмме, каждая точка в каждой точке на каком-либо уровне удаленного сегмента находится точка находится в бесконечно глубоком двоичном дереве, где путь проходит влево или вправо на каждом уровне в зависимости от того, на какой стороне удаленного сегмента находится точка. Представление каждого поворота влево с помощью 2 дает троичную дробь для точки. Замена цифр «2» в этих дробях цифрами «1» дает сюръективное (а не инъективное ) отображение между набором Кантора и набором двоичных дробей в интервале [0, 1].

Набор Кантора определен как набор не исключенных точек, доля (т. Е. такт ) оставшегося единичного интервала может быть найдена по общему длине удалена. Эта сумма равна геометрической прогрессии

$\sum \; n\; =\; 0\; \infty \; 2\; n\; 3\; n\; +\; 1\; =\; 1\; 3\; +\; 2\; 9\; +\; 4\; 27\; +\; 8\; 81\; +\; \cdots \; =\; 1\; 3\; (1\; 1\; -\; 2\; 3)\; =\; 1.\; \{\; \backslash \; displaystyle\; \backslash \; sum\; \_\; \{n\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{2\; ^\; \{n\}\}\; \{3\; ^\; \{n\; +\; 1\}\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; +\; \{\backslash \; frac\; \{2\}\; \{9\}\}\; +\; \{\backslash \; frac\; \{4\}\; \{27\}\}\; +\; \{\backslash \; frac\; \{8\}\; \{81\}\}\; +\; \backslash \; cdots\; =\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{\; 1\}\; \{1\; -\; \{\backslash \; frac\; \{2\}\; \{3\}\}\}\}\; \backslash \; right)\; =\; 1.\}$

Таким образом, соотношение слева равно 1 - 1 = 0.

Этот расчет предполагает, что набор Кантора не может содержать какой-либо интервал ненулевой длины. Может показаться удивительным, что что-то остаться - сумма удаленных интервалов равна длине исходного интервала. Однако более пристальный взгляд на процесс показывает, что происходит удаление «средней трети» каждого интервала связано с удалением открытых (наборов, которые не включают свои конечные точки). Таким образом, удаление отрезка (⁄ 3, ⁄ 3) из исходного интервала [0, 1] оставляет позади точки ⁄ 3 и ⁄ 3. Последующие шаги не удаляют эти (или другие) конечные точки, поскольку удаленные интервалы всегда являются внутренними по оставшимся интервалам. Таким образом, множество каналов не является пустым и включает в себя бесчисленное бесконечное количество точек (как следует из приведенного выше описания в терминах путей в бесконечном двоичном дереве).

Может показаться, что остались только концы строительных сегментов, но это тоже не так. Число ⁄ 4, например, имеет уникальную троичную форму 0,020202... = 0,02. Он находится в нижней трети, и в верхней трети этой трети, и в нижней трети этой верхней трети, и так далее. Он никогда не находится в одном из средних сегментов, он никогда не удаляется. Тем не менее, он не является конечной точкой какого-либо среднего сегмента, что он не является кратен какой-либо степени 1/3. Все конечные точки отрезков являются конечными троичными дробями и имеющимся в множестве

$\{x\; \in \; [0,\; 1]\; \mid \; \exists \; i\; \in \; N\; 0:\; x\; 3\; i\; \in \; Z\}\; (\subset \; N\; 0\; 3\; -\; N\; 0)\; \{\backslash \; displaystyle\; \backslash \; \{\; x\; \backslash \; in\; [0,1]\; \backslash \; mid\; \backslash \; exists\; i\; \backslash \; in\; \backslash \; mathbb\; \{N\}\; \_\; \{0\}:\; x\; \backslash ,\; 3\; ^\; \{i\}\; \backslash \; in\; \backslash \; mathbb\; \{Z\}\; \backslash \}\; \backslash \; qquad\; \{\backslash \; Bigl\; (\}\; \backslash \; subset\; \backslash \; mathbb\; \{N\}\; \_\; \{0\}\; \backslash ,\; 3\; ^\; \{-\; \backslash \; mathbb\; \{N\}\; \_\; \{0\}\}\; \{\backslash \; Bigr)\}\}$

который представляет собой счетно бесконечное множество. Что касается мощности, почти все элементы набора Кантора не являются конечными точками интервалов, и весь набор Кантора является не счетным.

Мощность

Можно показать, что в этом процессе осталось столько же точек, сколько было вначале, и, следовательно, множество Кантора бесчисленное множество. Чтобы убедиться в этом, мы показываем, что существует функция из набора Кантора $C\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{C\}\}\}$до закрытого интервала [0,1], который равен сюръективный (т.е. отображает из $C\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{C\}\}\}$на [0,1]), так что мощность $C\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{C\}\}\}$не меньше, чем [0,1]. $C\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{C\}\}\}$является подмножеством [0,1], его мощность также не больше, поэтому две мощности должны быть фактически равны, теорема Кантора - Бернштейна - Шредера.

Чтобы построить эту функцию, рассмотрим точки в интервале [0, 1] в терминах системы счисления с основанием 3 (или тро ). Напомним, что правильные троичные дроби, точнее: элементы $(Z\; \setminus \; \{0\})\; \cdot \; 3\; -\; N\; 0\; \{\backslash \; displaystyle\; \{\backslash \; bigl\; (\}\; \backslash \; mathbb\; \{Z\}\; \backslash \; smallsetminus\; \backslash \; \{0\; \backslash \}\; \{\backslash \; bigr)\}\; \backslash \; cdot\; 3\; ^\; \{-\; \backslash \; mathbb\; \{N\}\; \_\; \{0\}\}\}$, допускайте более одного представления в этой нотации, например, ⁄ 3, которые могут записывается как 0,1 3 = 0,10 3, но также как 0,0222... 3 = 0,02 3 и ⁄ 3, который можно записать как 0,2 3 = 0,20 3, но также как 0,1222... 3 = 0, 12 3. Когда мы удаляем среднюю третье, она содержит число с троичными цифрами вида 0.1xxxxx... 3, где xxxxx... 3 находится строго между 00000... 3 и 22222... 3. Таким образом, числа, оставшиеся после первого шага, состоят из

• чисел 0,0xxxxx... 3 (включая 0,022222... 3 = 1/3)
• Числа вида 0,2xxxxx... 3 (включая 0,222222... 3 = 1)

Это можно резюмировать, сказав, что эти число с троичными такое представление, что первая цифра после точки счисления не равно 1, - это цифры, оставшиеся после первого шага.

На втором этапе удаляются числа вида 0,01xxxx... 3 и 0,21xxxx... 3, и (с должным вниманием к конечным точкам) сделать вывод, что оставшиеся числа - это число с троичными числами, где ни одна из первых двух цифр не равна 1.

Продолжая таким образом, чтобы число не было исключено на шаге n, оно должно иметь троичную форму. Представление, n-я цифра, которого не соответствует 1. число входило в набор каналов, его нельзя исключить ни на каком этапе.

Следует отметить, что числа типа 1, ⁄ 3 = 0,1 3 и ⁄ 9 = 0,21 3 находятся в наборе Кантора, так как они имеют троичные числа, состоящие полностью из нулей и двоек: 1 = 0,222... 3 = 0,2 3, ⁄ 3 = 0,0222... 3 = 0,02 3 и ⁄ 9 = 0,20222... 3 = 0,202 3. Все последние числа являются «конечными точками», и эти примеры являются правильными предельными точками из $C\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{C\}\}\}$. То же самое верно для левых предельных точек $C\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{C\}\}\}$, e. грамм. ⁄ 3 = 0,1222... 3 = 0,12 3 = 0,20 3 и ⁄ 9 = 0,21222... 3 = 0,212 3 = 0,220 3. Все эти конечные точки являются собственно троичными дробями (элементы $Z\; \cdot \; 3\; -\; N\; 0\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{Z\}\; \backslash \; cdot\; 3\; ^\; \{-\; \backslash \; mathbb\; \{N\}\; \_\; \{0\}\}\}$) вида ⁄ q, где знаменатель q представляет собой степень 3, когда дробь находится в его несократимой форме. Тернарное представление этих дробей завершается (т. Конечно Е.) или - напомним, что каждая отдельная троичная дробь имеет 2 представления - бесконечно и «конечным» либо бесконечным числом повторяющихся нулей, либо бесконечным числом повторяющихся двоек. Такая дробь является левой предельной точкой $C\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{C\}\}\}$, если ее троичное представление не содержит элементов и «конечных» бесконечных повторяющихся нули. Точно так же правильная троичная дробь является правой предельной точкой $C\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{C\}\}\}$, если ее троичное расширение снова не содержит единиц и «конечных» бесконечным числом повторяющихся 2с.

Этот набор конечных точек плотный в $C\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{C\}\}\}$(но не плотный в [0, 1]) и составляет счетно бесконечное множество. Числа в $C\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{C\}\}\}$, которые не являются конечными точками, также имеют 0 и 2 в их троичном представлении, но они не могут заканчиваться бесконечным повторением. 0, ни цифры 2, потому что тогда это будет конечная точка.

Функция от $C\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{C\}\}\}$до [0,1] определяется путем взятия троичных чисел, которые полностью состоят из нулей и 2s, заменяя все 2 на 1 и интерпретировать последовательность как двоичное представление действительного числа. В формуле

$е\; (\sum \; k\; \in \; N\; ak\; 3\; -\; k)\; =\; \sum \; k\; \in \; N\; ak\; 2\; 2\; -\; k\; \{\backslash \; displaystyle\; f\; \{\backslash \; bigg\; (\}\; \backslash \; sum\; \_\; \{k\; \backslash \; in\; \backslash \; mathbb\; \{N\}\}\; a\_\; \{\; k\}\; 3\; ^\; \{-\; k\}\; \{\backslash \; bigg)\}\; =\; \backslash \; sum\; \_\; \{k\; \backslash \; in\; \backslash \; mathbb\; \{N\}\}\; \{\backslash \; frac\; \{a\_\; \{k\}\}\; \{2\}\}\; 2\; ^\; \{-\; k\}\}$, где $\forall \; k\; \in \; N:\; ak\; \in \; \{0,\; 2\}.\; \{\backslash \; displaystyle\; \backslash \; forall\; k\; \backslash \; in\; \backslash \; mathbb\; \{N\}:\; a\_\; \{k\}\; \backslash \; in\; \backslash \; \{0,2\; \backslash \}.\}$

Для любого числа y в [0,1] его двоичное представление можно преобразовать в троичное представление числа x в $C\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{C\}\}\}$путем замены всех единиц на 2. При этом f (x) = y, так что y находится в диапазоне е. Например, если y = ⁄ 5 = 0,100110011001... 2 = 0,1001, мы пишем x = 0.2002 = 0.200220022002... 3 = ⁄ 10. Следовательно, ф сюръективен. Однако f не является инъективным - значения, для которых f (x) совпадает, являются значениями на противоположных концах одной из удаленных средних третей. Например, возьмите

⁄3= 0,02 3 (что является правой предельной точкой $C\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{C\}\}\}$и левой предельной точкой средней трети [⁄ 3,⁄3]) и

⁄3= 0,20 3 (что является левой предельной точкой $C\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{C\}\}\}$и правая граничная точка средней трети [⁄ 3,⁄3])

поэтому

$f\; (1/3)\; =\; f\; (0,0\; 2\; ¯\; 3)\; =\; 0,0\; 1\; ¯\; 2\; =\; 0,1\; 2\; =\; 0,1\; 0\; ¯\; 2\; =\; е\; (0,2\; 0\; ¯\; 3)\; =\; е\; (2/3).\; \parallel \; 1/2\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{array\}\; \{lcl\}\; f\; \{\backslash \; bigl\; (\}\; \{\}\; ^\; \{1\}\; \backslash !\; \backslash !\; /\; \backslash !\; \_\; \{3\}\; \{\backslash \; bigr)\}\; =\; f\; (0,0\; \{\backslash \; overline\; \{2\}\}\; \_\; \{3\})\; =\; 0,0\; \{\backslash \; overline\; \{1\}\}\; \_\; \{2\}\; =\; \backslash !\; \backslash !\; \backslash !\; \backslash !\; 0.1\_\; \{2\}\; \backslash !\; \backslash !\; \backslash !\; \backslash !\; =\; 0,1\; \{\backslash \; overline\; \{0\}\}\; \_\; \{2\}\; =\; f\; (0,2\; \{\backslash \; overline\; \{0\}\}\; \_\; \{3\})\; =\; f\; \{\backslash \; bigl\; (\}\; \{\}\; ^\; \{2\}\; \backslash !\; \backslash !\; /\; \backslash !\; \_\; \{3\}\; \{\backslash \; bigr)\}.\; \backslash \backslash \; \backslash \; parallel\; \backslash \backslash \; \{\}\; ^\; \{1\}\; \backslash !\; \backslash !\; /\; \backslash !\; \_\; \{2\}\; \backslash \; end\; \{array\}\}\}$

Таким образом, количество точек вборе Кантора равно количеству точек в интервале [0, 1] (который имеет несчетное мощность $c\; =\; 2\; \aleph \; 0\; \{\backslash \; Displaystyle\; \{\backslash \; mathfrak\; \{с\; \}\}\; =\; 2\; ^\; \{\backslash \; aleph\; \_\; \{0\}\}\}$). Однако набор конечных точек удаленных интервалов равен countab le, поэтому в наборе каналов должно быть несчетное количество чисел, которые не являются конечными точками интервала. Как упомянуто выше, одним из примеров такого числа является ⁄ 4, которое может быть записано как 0,020202... 3 = 0,02 в троичной системе счисления. Фактически, для любого $a\; \in \; [-\; 1,\; 1]\; \{\backslash \; displaystyle\; a\; \backslash \; in\; [-1,1]\}$существует $x,\; y\; \in \; C\; \{\backslash \; displaystyle\; x,\; y\; \backslash \; в\; \{\backslash \; mathcal\; \{C\}\}\}$такой, что $a\; =\; y\; -\; x\; \{\backslash \; displaystyle\; a\; =\; yx\}$. Впервые это было продемонстрировано Штейнхаусом в 1917 году, доказал геометрический аргумент эквивалентное утверждение, что $\{(x,\; y)\; \in \; R\; 2\; |\; Y\; знак\; равно\; Икс\; +\; а\}\; \cap \; (С\; \times \; С)\; \ne \; \varnothing \; \{\backslash \; Displaystyle\; \backslash \; \{(х,\; у)\; \backslash \; в\; \backslash \; mathbb\; \{R\}\; ^\; \{2\}\; \backslash ,\; |\; \backslash ,\; у\; =\; х\; +\; а\; \backslash \}\; \backslash ;\; \backslash \; крышка\; \backslash ;\; (\{\backslash \; mathcal\; \{C\}\}\; \backslash \; times\; \{\backslash \; mathcal\; \{C\}\})\; \backslash \; neq\; \backslash \; emptyset\}$для каждого $a\; \in \; [-\; 1,\; 1]\; \{\backslash \; displaystyle\; a\; \backslash \; в\; [-\; 1,1]\}$. Эта установка обеспечивает инъекцию из $[-\; 1,\; 1]\; \{\backslash \; displaystyle\; [-1,1]\}$в $C\; \times \; C\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{C\}\}\; \backslash \; раз\; \{\backslash \; mathcal\; \{C\}\}\}$, мы имеем $|\; C\; \times \; C\; |\; \ge \; |\; [-\; 1,\; 1]\; |\; =\; с\; \{\backslash \; Displaystyle\; |\; \{\backslash \; mathcal\; \{C\}\}\; \backslash \; times\; \{\backslash \; mathcal\; \{C\}\}\; |\; \backslash \; geq\; |\; [-1,1]\; |\; =\; \{\backslash \; mathfrak\; \{c\}\}\}$как непосредственное следствие. Предполагая, что $|\; A\; \times \; A\; |\; =\; |\; А\; |\; \{\backslash \; displaystyle\; |\; А\; \backslash \; раз\; А\; |\; =\; |\; A\; |\}$для любого бесконечного множества $A\; \{\backslash \; displaystyle\; A\}$(выражение, эквивалентное аксиома выбора Тарского ), это еще одна демонстрация того, что $|\; C\; |\; =\; с\; \{\backslash \; Displaystyle\; |\; \{\backslash \; mathcal\; \{C\}\}\; |\; =\; \{\backslash \; mathfrak\; \{c\}\}\}$.

Набор Кантора содержит количество точек, сколько интервал, из которого он взят, но сам по себе не содержит интервалов ненулевой длины. У иррациональных чисел такое же свойство, но у числа Кантора есть дополнительное свойство замкнутости, поэтому оно даже не плотное в любом интервале, в отличие от иррациональных чисел, которые плотны в каждом интервале.

Было высказано предположение, что все алгебраические иррациональные числа являются нормальными. Все члены набора кантора не являются стандартными средствами набора, либо трансцендентны.

Самоподобие

Набор Кантора является прототипом фрактал. Это самоподобный, потому что он равен двум копиям самого себя, если каждая копия будет уменьшена в 3 и переведена. Точнее, множество каналов равно объединению двух функций, левого и правого преобразователя самоподобия, $TL\; (x)\; =\; x\; /\; 3\; \{\backslash \; displaystyle\; T\_\; \{L\}\; (x)\; =\; x\; /\; 3\}$и $TR\; (x)\; =\; (2\; +\; x)\; /\; 3\; \{\backslash \; displaystyle\; T\_\; \{R\}\; (x)\; =\; (2\; +\; x)\; /\; 3\}$, которые оставляют канторовское множество инвариантным с точностью до гомеоморфизма : $TL\; (C)\; \cong \; TR\; (C)\; \cong \; C\; =\; TL\; (C)\; \cup \; TR\; (C).\; \{\backslash \; displaystyle\; T\_\; \{L\}\; (\{\backslash \; mathcal\; \{C\}\})\; \backslash \; cong\; T\_\; \{R\}\; (\{\backslash \; mathcal\; \{C\}\})\; \backslash \; cong\; \{\backslash \; mathcal\; \{C\}\}\; =\; T\_\; \{L\}\; (\{\backslash \; mathcal\; \{\; C\}\})\; \backslash \; cup\; T\_\; \{R\}\; (\{\backslash \; mathcal\; \{C\}\}).\}$

Повторяющаяся итерация из $TL\; \{\backslash \; displaystyle\; T\_\; \{L\}\}$и $TR\; \{\backslash \; displaystyle\; T\_\; \{R\}\}$можно визуализировать как бесконечное двоичное дерево. То есть в каждом узле дерева можно рассматривать поддерево слева или справа. Если взять набор $\{TL,\; TR\}\; \{\backslash \; displaystyle\; \backslash \; \{T\_\; \{L\},\; T\_\; \{R\}\; \backslash \}\}$вместе с композицией функций, образует моноид, диадический моноид.

автоморфизмы двоичного дерева обеспечивают его гиперболическими вращениями и задаются модульной группой. Таким образом, множество Кантора представляет собой однородное пространство в том смысле, что для любых двух точек $x\; \{\backslash \; displaystyle\; x\}$и $y\; \{\backslash \; displaystyle\; y\}$в наборе Кантора $C\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{C\}\}\}$существует гомеоморфизм $h:\; C\; \to \; C\; \{\backslash \; displaystyle\; h:\; \{\backslash \; mathcal\; \{C\}\; \}\; \backslash \; to\; \{\backslash \; mathcal\; \{C\}\}\}$с $h\; (x)\; =\; y\; \{\backslash \; displaystyle\; h\; (x)\; =\; y\}$. Явное построение $h\; \{\backslash \; displaystyle\; h\}$будет проще описать, если мы рассмотрим набор каналов как пространство произведения счетного числа копий дискретного пространства $\{0,\; 1\}\; \{\backslash \; displaystyle\; \backslash \; \{0,1\; \backslash \}\}$. Тогда карта $h:\; \{0,\; 1\}\; N\; \to \; \{0,\; 1\}\; N\; \{\backslash \; displaystyle\; h:\; \backslash \; \{0,1\; \backslash \}\; ^\; \{\backslash \; mathbb\; \{N\}\}\; \backslash \; to\; \backslash \; \{0,1\; \backslash \}\; ^\; \{\backslash \; m\; athbb\; \{N\}\}\}$определено $hn\; (u):\; =\; un\; +\; xn\; +\; yn\; mod\; 2\; \{\backslash \; displaystyle\; h\_\; \{n\}\; (u):\; =\; u\_\; \{n\}\; +\; x\_\; \{n\}\; +\; y\_\; \{n\}\; \backslash \; mod\; 2\}$- инволютивный гомеоморфизм, заменяющий $x\; \{\backslash \; displaystyle\; x\}$и $y\; \{\backslash \; displaystyle\; y\}$.

Закон сохранение

Было обнаружено, что некоторая форма сохранения всегда отвечает за масштаб и самоподобие. В случае набора Кантора можно видеть, что $df\; \{\backslash \; displaystyle\; d\_\; \{f\}\}$th момент (где $df\; =\; ln\; \; (2)\; /\; ln\; \; (3)\; \{\backslash \; displaystyle\; d\_\; \{f\}\; =\; \backslash \; ln\; (2)\; /\; \backslash \; ln\; (3)\}$- фрактальная размерность) всех уцелевших интервалов на любом этапе построения равно константе, которая равна единице в множестве Кантора. Мы знаем, что существуют $N\; =\; 2\; n\; \{\backslash \; displaystyle\; N\; =\; 2\; ^\; \{n\}\}$интервалы размером $1/3\; n\; \{\backslash \; displaystyle\; 1/3\; ^\; \{n\}\}$присутствует в системе на $n\; \{\backslash \; displaystyle\; n\}$-м шаге ее построения. Затем, если мы обозначим оставшиеся интервалы как $x\; 1,\; x\; 2,\dots ,\; x\; 2\; n\; \{\backslash \; displaystyle\; x\_\; \{1\},\; x\_\; \{2\},\; \backslash \; ldots,\; x\_\; \{2\; ^\; \{n\}\}\}$тогда $df\; \{\backslash \; displaystyle\; d\_\; \{f\}\}$th момент равен $x\; 1\; df\; +\; x\; 2\; df\; +\; \cdots \; +\; x\; 2\; ndf\; =\; 1\; \{\backslash \; displaystyle\; x\_\; \{1\}\; ^\; \{d\_\; \{f\}\}\; +\; x\_\; \{2\}\; ^\; \{d\_\; \{f\}\}\; +\; \backslash \; cdots\; +\; x\_\; \{2\; ^\; \{n\}\}\; ^\; \{d\_\; \{f\}\}\; =\; 1\}$поскольку $Икс\; 1\; =\; Икс\; 2\; =\; \cdots \; =\; Икс\; 2\; N\; =\; 1/3\; n\; \{\backslash \; Displaystyle\; x\_\; \{1\}\; =\; x\_\; \{2\}\; =\; \backslash \; cdots\; =\; x\_\; \{2\; ^\; \{n\}\}\; =\; 1/3\; ^\; \{n\}\}$.

Размерность Хаусдорфа канторовского числа равна ln (2) / ln (3) ≈ 0,631.

Топологические и аналитические свойства

Хотя "канторовское множество обычно относится к исходному канторовскому множеству средней трети, описанному выше, топологи часто говорят о" "канторовском множестве, что означает любое топологическое пространство то есть гомеоморфно (топологически эквивалентно) ему.

Как показывает приведенный выше аргумент суммирования, множество Кантора неисчислимо, но имеет меру Лебега 0. Множество Кантора является дополнением союз из открытого множеств, оно является само закрытым подмножеством вещественных чисел и, следовательно, полным метрическое пространство. Он также вполне ограничен, теорема Гейне - Бореля гласит, что он должен компактным.

Для любой точки множества канального и любого сколь угодно малой окрестности точки, есть другое число с троичными числами, состоящее только из нулей и двоек, а также числа, троичные цифры содержат единицы. Следовательно, каждая точка в наборе Кантора является точкой накопления (также называемой точкой кластера или предельной точкой) Кантора, но ни одна из них не является точкой набора. Замкнутое множество, в каждой точке которого является точка накопления, также называется совершенным множеством в топологии, в то время как замкнутое подмножество интервала без внутренних точек нигде не плотно антракте.

Каждая точка набора Кантора также является точкой набора дополнения набора Кантора.

Для любых двух точек в наборе Кантора будет некоторая троичная цифра, где они различаются - одна будет иметь 0, а другую 2. Путем разделения набора Кантора на «половинки» в зависимости от значений этой цифры, получается разбиение множества Кантора на два замкнутых числа, разделяющих исходные две точки. В относительной топологии в наборе Кантора точки были разделены закрытым набором. Следовательно, набор Кантора полностью отключен. Как компактное полностью несвязное хаусдорфово пространство, множество Кантора является примером каменного пространства.

В качестве топологического пространства множество Кантора естественно гомеоморфно к продукту из счетного числа копий пространства $\{0,\; 1\}\; \{\backslash \; displaystyle\; \backslash \; \{0,1\; \backslash \}\}$, где каждая копия несет в себе дискретную топологию . Это пространство всех последовательностей из двух цифр

$2\; N\; =\; \{(xn)\; \mid \; xn\; \in \; \{0,\; 1\}\; для\; n\; \in \; N\}\; \{\backslash \; displaystyle\; 2\; ^\; \{\backslash \; mathbb\; \{N\}\}\; =\; \backslash \; \{(x\_\; \{n\})\; \backslash \; mid\; x\_\; \{n\}\; \backslash \; in\; \backslash \; \{0,1\; \backslash \}\; \{\backslash \; text\; \{for\}\}\; n\; \backslash \; in\; \backslash \; mathbb\; \{N\}\; \backslash \}\}$,

который также может быть идентифицируется с набором 2-адических целых чисел. Основой для открытых наборов топологии продукта являются цилиндрические наборы ; гомеоморфизм отображает их в топологию подпространства , которую канторовский набор наследует от топологии на прямой действительной числовой линии. Эта характеристика канторовского пространства как произведения компактных пространств дает второе доказательство компактности канторовского пространства с теоремы Тихонова.

. Из приведенной выше характеристики канторов множества гомеоморфно p-адические числа, и, если из него удалить одну точку, на p-адические числа.

, Множество Кантора - это подмножество вещественных чисел, которые являются метрическим пространством по отношению к метрике обычного расстояния ; Следовательно, множество средств само по себе по метрическому пространству с использованием той же метрики. В качестве альтернативы можно использовать p-адическую метрику на $2\; N\; \{\backslash \; displaystyle\; 2\; ^\; \{\backslash \; mathbb\; \{N\}\}\}$: с учетом двух последовательностей $(xn),\; (yn)\; \in \; 2\; N\; \{\backslash \; displaystyle\; (x\_\; \{n\}),\; (y\_\; \{n\})\; \backslash \; in\; 2\; ^\; \{\backslash \; mathbb\; \{N\}\}\}$, расстояние между ними $d\; ((xn),\; (yn))\; =\; 2\; -\; k\; \{\backslash \; displaystyle\; d\; ((x\_\; \{n\}),\; (y\_\; \{n\}))\; =\; 2\; ^\; \{-\; k\}\}$, где $k\; \{\backslash \; displaystyle\; k\}$- наименьший индекс, такой что $xk\; \ne \; yk\; \{\backslash \; displaystyle\; x\_\; \{k\}\; \backslash \; neq\; y\_\; \{k\}\}$; если такого указателя нет, то две совпадают, и одна определяет расстояние равным нулю. Эти две метрики генерируют одинаковую топологию на множестве Кантора.

Выше мы видели, что оно полностью несвязным совершенным компактным метрическим пространством. В самом деле, в некотором смысле оно единственное: всякое непустое вполне несвязное совершенное компактное метрическое пространство гомеоморфно канторову множеству. См. пространство Кантора для постоянной информации о пространствех, гомеоморфных множеств Кантора.

Каналовское множество иногда считается "универсальным" в категории из компактных метрических пространств, любое компактное метрическое пространство является непрерывным изображением множества Кантора; однако эта конструкция не уникальна, и поэтому множество каналов не является универсальным в точном категориальном смысле. «Универсальное» свойство имеет важные приложения в функциональном анализе, где оно иногда известно как теорема представления для компактных метрических пространств.

Для любого целого числа q ≥ 2 топология в группе G = Zq(счетная прямая сумма) дискретна. Хотя дуальный по Понтрягину Γ также является Zq, топология Γ компактна. Видно, что Γ полностью несвязна и совершенна, а значит, гомеоморфна канторову множеству. Гомеоморфизм проще всего выписать явно в случае q = 2. (См. Рудин 1962, стр. 40.)

Среднее геометрическое набора Кантора составляет приблизительно 0,274974.

Мера и вероятность

Набор Кантора можно рассматривать как компактную группу двоичных последовательностей, и, как таковую, она наделена естественной мерой Хаара. При нормализации таким образом, что размер набора равен 1, он представляет собой модель бесконечной последовательности подбрасываний монеты. Кроме того, можно показать, что обычная мера Лебега на интервале является мерой Хаара на канторовом множестве, в то время как естественная инъекция в тройном множестве каноническим примером сингулярной меры. Также можно показать, что мера Хаара является образом любой вероятности, что в некотором смысле делает множество кантора универсальным вероятностным пространством.

В теории меры Лебега множество Кантора примером несчетного множества с нулевой мерой.

Числа Кантора

Если определено число Кантора как член набора Кантора, тогда

• (1) Каждое действительное число в [0, 2] является суммой двух чисел Кантора.
• (2) Между любыми числами существует число, не являющееся числом Кантора.

Теория описательных множеств

Набор Кантора - это скудный набор (или набор первой категории) как подмножество [0, 1] (хотя и не как подмножество самого себя, поскольку это пространство Бэра ). Таким образом, множество Кантора демонстрирует, что понятия «размер» с точки зрения, меры и категории (Бэра). Как и набор $Q\; \cap \; [0,\; 1]\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{Q\}\; \backslash \; cap\; [0,1]\}$, набор Кантора $C\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{C\; \}\}\}$является «маленьким» в том смысле, что это нулевой набор (набор нулевой меры), и это скудное подмножество [0,1]. Однако, в отличие от $Q\; \cap \; [0,\; 1]\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{Q\}\; \backslash \; cap\; [0,1]\}$, который является счетным и имеет «маленькую» мощность, $\aleph \; 0\; \{\backslash \; displaystyle\; \backslash \; aleph\; \_\; \{0\}\}$, мощность $C\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{C\}\}\}$такая же, как у [0, 1], континуум $c\; \{\backslash \; displaystyle\; \{\backslash \; mathfrak\; \{c\}\}\}$, и является «большим» в смысле мощности. Фактически, также возможно построить подмножество [0,1], которое является скудным, но с положительной мерой, и подмножество, которое не является скудным, но с нулевой мерой: взяв счетное объединение «толстых» канторовских множеств $С\; (n)\; \{\; \backslash \; displaystyle\; \{\backslash \; mathcal\; \{C\}\}\; ^\; \{(n)\}\}$меры $\lambda \; =\; (n\; -\; 1)\; /\; n\; \{\backslash \; displaystyle\; \backslash \; lambda\; =\; (n\; -1)\; /\; n\}$(см. Набор Смита - Вольтерры - Кантора ниже для построения), мы получаем набор $A:\; =\; \bigcup \; n\; =\; 1\; \infty \; C\; (n)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{A\}\}:\; =\; \backslash \; bigcup\; \_\; \{n\; =\; 1\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; mathcal\; \{C\}\}\; ^\; \{(n)\}\}$с положительной мерой (равной 1) но скудный в [0,1], поскольку каждый $C\; (n)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{C\}\}\; ^\; \{(n)\}\}$нигде является не плотным. Затем рассмотрим набор $A\; c\; =\; [0,\; 1]\; \setminus \; \bigcup \; n\; =\; 1\; \infty \; C\; (n)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{A\}\}\; ^\; \{\backslash \; mathrm\; \{c\}\}\; =\; [0,1]\; \backslash \; setminus\; \backslash \; bigcup\; \_\; \{n\; =\; 1\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; mathcal\; \{C\}\}\; ^\; \{(n)\}\}$. $A\; \cup \; A\; c\; =\; [0,\; 1]\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{A\}\}\; \backslash \; cup\; \{\backslash \; mathcal\; \{A\}\}\; ^\; \{\backslash \; mathrm\; \{c\}\}\; =\; [0,1]\}$, $A\; c\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{A\}\}\; ^\; \{\backslash \; mathrm\; \{c\}\}\}$не может быть скудным, но поскольку $\mu \; (A)\; =\; 1\; \{\backslash \; displaystyle\; \backslash \; mu\; (\; \{\backslash \; mathcal\; \{A\}\})\; =\; 1\}$, $A\; c\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{A\}\}\; ^\; \{\backslash \; mathrm\; \{c\}\}\}$должен иметь нулевую меру.

Набор Смита - Вольтерры - Кантора

Вместо многократного удаления средней трети каждого элемента, как в наборе Кантора, мы могли бы также удалить любой другой фиксированный процент (кроме 0 % и 100%) от середины. В случае, когда середина ⁄ 10 интервала удалена, мы получаем замечательно доступный случай - набор из всех чисел в [0,1], которые могут быть записаны в виде десятичной дроби, состоящей полностью из нулей. и 9с. Если фиксированный процент удаляется на каждом этапе, то ограничивающий набор будет иметь нулевую меру, поскольку длина остатка $(1\; -\; f)\; n\; \to \; 0\; \{\backslash \; displaystyle\; (1-f)\; ^\; \{n\}\; \backslash \; to\; 0\}$как $n\; \to \; \infty \; \{\backslash \; displaystyle\; n\; \backslash \; to\; \backslash \; infty\}$для любого такого, что .

с другой стороны, «толстые наборы Кантора» положительных мера может быть сгенерирована удалением более мелких частей середины сегмента на каждую итерации. Таким образом, можно построить множество, гомеоморфные множеству Кантора, которые имеют положительную меру Лебега, но при этом нигде не плотны. Если интервал длины297>rn {\ displaystyle r ^ {n}}($r\; \le \; 1/3\; \{\backslash \; displaystyle\; r\; \backslash \; leq\; 1/3\}$) удаляется из середины каждого сегмент на n-й итерации, тогда общая удаленная длина равна $\sum \; n\; =\; 1\; \infty \; 2\; n\; -\; 1\; rn\; =\; r\; /\; (1-2\; r)\; \{\backslash \; textstyle\; \backslash \; sum\; \_\; \{n\; =\; 1\}\; ^\; \{\backslash \; infty\}\; 2\; ^\; \{\; n-1\}\; r\; ^\; \{n\}\; =\; r\; /\; (1-2r)\}$, и предельный набор будет иметь меру Лебега, равную $\lambda \; =\; (1\; -\; 3\; r)\; /\; (1-2\; r)\; \{\backslash \; displaystyle\; \backslash \; lambda\; =\; (1-3r)\; /\; (1-2r)\}$. Таким образом, в некотором смысле канторовский набор средних третей является предельным случаем с $r\; =\; 1/3\; \{\backslash \; displaystyle\; r\; =\; 1/3\}$. Если , то остаток будет иметь положительную величину с . Случай $r\; =\; 1/4\; \{\backslash \; displaystyle\; r\; =\; 1/4\}$известен как набор Смита – Вольтерра – Кантора, у которого мера Лебега $1/2\; \{\backslash \; displaystyle\; 1/2\}$.

Стохастический набор Кантора

Можно изменить конструкцию набора Кантора путем случайного деления, а не равного. Кроме того, чтобы включить время, мы можем разделить только один из доступных интервалов на каждом шаге вместо того, чтобы делить все доступные интервалы. В случае стохастического триадного множества Кантора результирующий процесс можно описать следующим уравнением скорости

$\partial \; c\; (x,\; t)\; \partial \; t\; =\; -\; x\; 2\; 2\; c\; (x,\; t)\; +\; 2\; \int \; x\; \infty \; (y\; -\; х)\; с\; (y,\; t)\; dy,\; \{\backslash \; displaystyle\; \{\{\backslash \; partial\; c\; (x,\; t)\}\; \backslash \; over\; \{\backslash \; partial\; t\}\}\; =\; -\; \{\{x\; ^\; \{2\}\}\; \backslash \; over\; \{2\}\}\; c\; (\; x,\; t)\; +2\; \backslash \; int\; \_\; \{x\}\; ^\; \{\backslash \; infty\}\; (yx)\; c\; (y,\; t)\; \backslash ,\; dy,\}$

и для стохастического диадического множества Кантора

$\partial \; c\; (x,\; t)\; \partial \; T\; знак\; равно\; -\; xc\; (x,\; t)\; +\; (1\; +\; p)\; \int \; x\; \infty \; c\; (y,\; t)\; dy,\; \{\backslash \; displaystyle\; \{\{\backslash \; partial\; c\; (x,\; t)\}\; \backslash \; over\; \{\backslash \; partial\; t\}\}\; =\; -xc\; (x,\; t)\; +\; (1\; +\; p)\; \backslash \; int\; \_\; \{x\}\; ^\; \{\backslash \; infty\}\; c\; (y,\; t)\; \backslash ,\; dy,\}$

где $c\; (x,\; t)\; dx\; \{\backslash \; displaystyle\; c\; (x,\; t)\; dx\}$- количество интервалов размера между $x\; \{\backslash \; displaystyle\; x\}$и $x\; +\; dx\; \{\backslash \; displaystyle\; х\; +\; dx\}$. В случае триадического набора Кантора фрактальная размерность равна $0,5616\; \{\backslash \; displaystyle\; 0,5616\}$, что меньше его детерминированного аналога $0,6309\; \{\backslash \; displaystyle\; 0.6309\}$. В случае стохастического диадического набора Кантора фрактальная размерность равна $p\; \{\backslash \; displaystyle\; p\}$, что снова меньше, чем у его детерминированного аналога $ln\; \; (1\; +\; p)\; /\; ln\; \; 2\; \{\backslash \; Displaystyle\; \backslash \; ln\; (1\; +\; p)\; /\; \backslash \; ln\; 2\}$. В случае стохастического диадического метода Кантора установить решение для $c\; (x,\; t)\; \{\backslash \; displaystyle\; c\; (x,\; t)\}$демонстрирует динамическое масштабирование в качестве своего решения в долгосрочное ограничение составляет $t\; -\; (1\; +\; df)\; e\; -\; xt\; \{\backslash \; displaystyle\; t\; ^\; \{-\; (1\; +\; d\_\; \{f\})\}\; e\; ^\; \{-\; xt\}\}$где фрактал размерность стохастического диадического набора Кантора $df\; =\; p\; \{\backslash \; displaystyle\; d\_\; \{f\}\; =\; p\}$. В любом случае, как и триадный набор Кантора, $df\; \{\backslash \; displaystyle\; d\_\; \{f\}\}$th момент ($\int \; xdfc\; (x,\; t)\; dx\; =\; constant\; \{\backslash \; displaystyle\; \backslash \; int\; x\; ^\; \{d\_\; \{f\}\}\; c\; (x,\; t)\; dx\; =\; \{\backslash \; text\; \{constant\}\}\}$) стохастического триадического и диадического канторовского множества также являются сохраняемыми величинами.

пыль Кантора

пыль Кантора - это многомерная версия множества Кантора. Его можно сформировать, взяв на себя конечное декартово произведение канторовского множества, сделав его канторовым пространством. Как и в наборе Кантора, пыль Кантора имеет нулевую меру.

кубы Кантора прогрессию рекурсии в сторону пыли Кантора

пыль Кантора (2D)

пыль Кантора (3D)

Другой 2D-аналог набора Кантора - ковер Серпинского, где квадрат разделен на девять меньших квадратов, средний удален. Затем оставшиеся квадраты делятся на девять, а середина удаляется, и так оставшиеся до бесконечности. Одним из трехмерных аналогов этого является губка Менгера.

. Кристофер Домас представил интерактивный инструмент двоичной визуализации на основе канторской пыли на Black Hat USA 2012.

Заглавная буква столбца с рисунком, напоминающим набором Кантора, но выраженная в двоичной, а не троичной форме. Гравюра Иль-де-Фил из «Описание египта» Жана-Батиста Проспера Жоллуа и Эдуарда Девилье, Imprimerie Impériale, Париж, 1809-1828 гг.

Сам Кантор определил в общем, абстрактном смысле и абстрактном тройную конструкцию в качестве примера более общей идеи, идеальное множество , которое является нигде не плотным. В оригинальной статье представлены несколько различных конструкций абстрактной концепции.

Этот набор считался абстрактным в то время, когда его изобрел Кантор. Сам Кантор пришел к этому из-за практических соображений по поводу набора точек, в которых тригонометрический ряд может не сойтись. Это открытие во многом подтолкнуло его к разработке абстрактной общей теории бесконечных множеств.

• Множество Смита - Вольтерры - Кантора
• Гексаграммы (И Цзин)
• Функция Кантора
• Куб Кантора
• Ожерелье Антуана
• Снежинка Коха
• Веер Кнастера - Куратовски
• Список фракталов по измерению Хаусдорфа
• Последовательность Мозера - де Брейна

• , Энциклопедия математики, EMS Press, 2001 [ 1994]
• Наборы Кантора и Наборы и функции Кантора в резать узел
• Сет Кантора в Платонических царствах