| Алгебраические структуры |
|---|
| Группа -как Теория групп |
Кольцо -как
|
| Lattice -как |
| Модуль- подобный |
| Алгебра- подобный |
|
 Алгебраические структуры между магмами и группами. Например, моноиды - это полугруппы с идентичностью.
Алгебраические структуры между магмами и группами. Например, моноиды - это полугруппы с идентичностью. В абстрактной алгебре, разделе математики, моноид - это набор, снабженный ассоциативной бинарной операцией и элементом идентичности.
Моноиды - это полугруппы с единицей. Такие алгебраические структуры встречаются в нескольких разделах математики.
Например, функции из набора в себя образуют моноид по отношению к композиции функций. В более общем плане в теории категорий морфизмы объекта к самому себе образуют моноид, и, наоборот, моноид можно рассматривать как категорию с одним объектом.
В информатике и программировании набор строк, построенных из заданного набора символов, является свободным моноидом. Моноиды перехода и синтаксические моноиды используются при описании конечных автоматов. Микроэлементы моноиды и история моноиды обеспечивают основу для процесса конкрементов и параллельного вычисления.
В теоретической информатике изучение моноидов является фундаментальным для теории автоматов ( теория Крона – Родса ) и теории формального языка ( проблема высоты звезды ).
Историю предмета и некоторые другие общие свойства моноидов см. В разделе « Полугруппа».
Набор S оснащен бинарной операцией S × S → S, который мы будем обозначать • является моноид, если она удовлетворяет следующим двум аксиомам:
Другими словами, моноид - это полугруппа с единичным элементом. Его также можно рассматривать как магму с ассоциативностью и идентичностью. Единичный элемент моноида уникален. По этой причине идентичность рассматривается как постоянная, то есть 0-арная (или нулевая) операция. Таким образом, моноид характеризуется заданием тройки ( S, •, e).
В зависимости от контекста, символ двоичной операции может быть опущен, так что операция обозначается сопоставлением; например, аксиомы моноида могут быть записаны как ( ab) c = a ( bc) и ea = ae = a. Это обозначение не означает, что это умножаемые числа.
Моноид, в котором каждый элемент имеет обратный, является группой.
Подмоноид моноида ( М, •) является подмножеством N из M, замкнутая относительно операций моноидных и содержит единичный элемент е из М. Символично, Н является подмоноид M, если N ⊆ М, х • у ∈ N всякий раз, когда х, у ∈ N, и е ∈ N. В этом случае N является моноидом под бинарной операцией, унаследованной от М.
С другой стороны, если N - подмножество моноида, которое закрывается при операции моноида, и является моноидом для этой унаследованной операции, то N не всегда является подмоноидом, поскольку элементы идентичности могут различаться. Например, одноэлементный набор {0} замкнут относительно умножения и не является подмоноидом (мультипликативного) моноида неотрицательных целых чисел.
Подмножество S из М называется генерации М, если наименьшая подмоноид М, содержащий S является М. Если существует конечное множество, порождающее M, то M называется конечно порожденным моноидом.
Моноид, операция которого коммутативна, называется коммутативным моноидом (или, реже, абелевым моноидом). Коммутативные моноиды часто пишутся аддитивно. Любой коммутативный моноид наделен своим алгебраическим предпорядком ≤, определяемым как x ≤ y, если существует z такое, что x + z = y. Порядковая единица коммутативного моноида M - это такой элемент u из M, что для любого элемента x из M существует v в множестве, порожденном u, такое, что x ≤ v. Это часто используется в случае, если М представляет собой положительный конус из частично упорядоченной абелевой группы G, и в этом случае мы говорим, что у есть порядок-единица G.
Моноид, для которого операция коммутативна для некоторых, но не для всех элементов, является моноидом следа ; Моноиды трассировки обычно встречаются в теории параллельных вычислений.
Из аксиом моноида следует, что единичный элемент e уникален: если e и f - единичные элементы моноида, то e = ef = f.
Для каждого неотрицательного целого числа n можно определить произведение любой последовательности из n элементов моноида рекурсивно: пусть p 0 = e и пусть p m = p m −1 • a m для 1 ≤ m ≤ n.
В качестве частного случая можно определить целые неотрицательные степени элемента x моноида: x 0 = 1 и x n = x n −1 • x для n ≥ 1. Тогда x m + n = x m • x n для всех m, n ≥ 0.
Элемент x называется обратимым, если существует такой элемент y, что x • y = e и y • x = e. Элемент y называется обратным к x. Обратные, если они существуют, уникальны: если y и z являются обратными x, то по ассоциативности y = ey = ( zx) y = z ( xy) = ze = z.
Если x обратим, скажем, с обратным y, то можно определить отрицательные степени x, положив x - n = y n для каждого n ≥ 1 ; это делает уравнение х т + п = х м • х п выполняться для всех т, п ∈ Z.
Множество всех обратимых элементов в моноиде вместе с операцией • образует группу.
Не каждый моноид находится внутри группы. Например, вполне возможно иметь моноид, в котором существуют два элемента a и b, такие, что выполняется a • b = a, даже если b не является тождественным элементом. Такой моноид не может быть вложен в группу, потому что в группе умножение обеих сторон на обратное к a приведет к тому, что b = e, что неверно.
Моноид ( M, •) обладает свойством сокращения (или является сокращающим), если для всех a, b и c в M равенство a • b = a • c влечет b = c, а равенство b • a = c • a влечет b = c.
Коммутативный моноид со свойством сокращения всегда может быть вложен в группу с помощью групповой конструкции Гротендика. Таким образом аддитивная группа целых чисел (группа с операцией +) строится из аддитивного моноида натуральных чисел (коммутативный моноид с операцией + и свойством сокращения). Однако некоммутативный сократительный моноид не обязательно должен быть вложен в группу.
Если моноид обладает свойством сокращения и конечен, то это фактически группа.
Правый и левый сократительные элементы моноида, каждый, в свою очередь, образуют подмоноид (т. Е. Замкнуты относительно операции и, очевидно, включают тождество). Это означает, что сокращающие элементы любого коммутативного моноида могут быть расширены до группы.
Свойство сокращения в моноиде не обязательно для выполнения конструкции Гротендика - достаточно коммутативности. Однако, если коммутативный моноид не обладает свойством сокращения, гомоморфизм моноида в его группу Гротендика не инъективен. Точнее, если a • b = a • c, то b и c имеют один и тот же образ в группе Гротендика, даже если b ≠ c. В частности, если моноид имеет поглощающий элемент, то его группа Гротендика является тривиальной группой.
Обратный моноид это моноид, где для каждого а в М, существует единственное A -1 в М таким образом, что = • -1 • и -1 = -1 • • -1. Если обратный моноид сокращается, то это группа.
В противоположном направлении, моноид без нуля представляет собой аддитивно записанный моноид, в котором a + b = 0 означает, что a = 0 и b = 0: эквивалентно, что никакой элемент, отличный от нуля, не имеет аддитивного обратного.
Пусть M - моноид, бинарная операция которого обозначается символом •, а единичный элемент - буквой e. Тогда (левый) M -акт (или левый полигон над M) - это множество X вместе с операцией ⋅: M × X → X, которая совместима со структурой моноида следующим образом:
Это аналог действия (левой) группы в теории моноидов. Аналогично определяются правые M -акты. Моноид с актом также известен как операторный моноид. Важные примеры включают переходные системы из semiautomata. Преобразование полугруппа может быть превращена в операторе моноид присоединения тождественного преобразования.
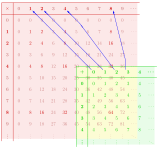 Пример гомоморфизма моноида x ↦ 2 x из ( N, +, 0) в ( N, ×, 1). Это инъективно, но не сюръективно.
Пример гомоморфизма моноида x ↦ 2 x из ( N, +, 0) в ( N, ×, 1). Это инъективно, но не сюръективно. Гомоморфизм между двумя моноидами ( М, *) и ( N, •) является функцией F : M → N такое, что
где e M и e N - тождества на M и N соответственно. Гомоморфизмы моноидов иногда называют просто морфизмами моноидов.
Не каждый гомоморфизм полугрупп между моноидами является гомоморфизмом моноидов, так как он может не отображать идентичность в идентичность целевого моноида, даже если идентичность является идентичностью образа гомоморфизма. Например, рассмотрим набор классов вычетов по модулю, снабженный умножением. В частности, классом является тождество. Функция, заданная в, является гомоморфизмом полугрупп, как в. Однако, таким образом, гомоморфизм моноидов - это гомоморфизм полугрупп между моноидами, который отображает идентичность первого моноида в идентичность второго моноида, и последнее условие не может быть опущено.
Напротив, гомоморфизм полугруппы между группами всегда является гомоморфизмом группы, поскольку он обязательно сохраняет идентичность (потому что в группе идентичность - единственный элемент, такой что x ⋅ x = x).
Биективен Моноид гомоморфизм называется моноидом изоморфизмом. Два моноида называются изоморфными, если между ними существует изоморфизм моноидов.
Моноидам можно дать представление, почти так же, как группы могут быть определены посредством группового представления. Это достигается путем задания набора образующих Σ и набора отношений на свободном моноиде Σ ∗. Это можно сделать, расширив (конечные) бинарные отношения на Σ ∗ до моноидных конгруэнций, а затем построив фактор-моноид, как указано выше.
Для бинарного отношения R ⊂ Σ ∗ × Σ ∗ его симметричное замыкание определяется как R ∪ R −1. Это может быть расширено до симметричного отношения E ⊂ Σ ∗ × Σ ∗, определяя x ∼ E y тогда и только тогда, когда x = sut и y = svt для некоторых строк u, v, s, t ∈ Σ ∗ с ( u, v) ∈ R ∪ R −1. Наконец, берется рефлексивное и транзитивное замыкание E, которое тогда является моноидной конгруэнцией.
В типичной ситуации отношение R просто задается в виде набора уравнений, так что. Так, например,
является эквациональным представлением бициклического моноида, а
- пластический моноид степени 2 (бесконечный порядок). Элементы этого пластического моноида могут быть записаны как целые числа i, j, k, поскольку соотношения показывают, что ba коммутирует как с a, так и с b.
| Групповые структуры | |||||
|---|---|---|---|---|---|
| Тотальность | Ассоциативность | Личность | Обратимость | Коммутативность | |
| Полугрупоидный | Ненужный | Необходимый | Ненужный | Ненужный | Ненужный |
| Малая категория | Ненужный | Необходимый | Необходимый | Ненужный | Ненужный |
| Группоид | Ненужный | Необходимый | Необходимый | Необходимый | Ненужный |
| Магма | Необходимый | Ненужный | Ненужный | Ненужный | Ненужный |
| Квазигруппа | Необходимый | Ненужный | Ненужный | Необходимый | Ненужный |
| Единая Магма | Необходимый | Ненужный | Необходимый | Ненужный | Ненужный |
| Петля | Необходимый | Ненужный | Необходимый | Необходимый | Ненужный |
| Полугруппа | Необходимый | Необходимый | Ненужный | Ненужный | Ненужный |
| Моноид | Необходимый | Необходимый | Необходимый | Ненужный | Ненужный |
| Коммутативный моноид | Необходимый | Необходимый | Необходимый | Ненужный | Необходимый |
| Группа | Необходимый | Необходимый | Необходимый | Необходимый | Ненужный |
| Абелева группа | Необходимый | Необходимый | Необходимый | Необходимый | Необходимый |
| ^ α Замыкание, которое используется во многих источниках, является аксиомой, эквивалентной тотальности, хотя и определяется по-другому. | |||||
Моноиды можно рассматривать как особый класс категорий. В самом деле, аксиомы, требуемые от операции моноида, в точности соответствуют аксиомам композиции морфизмов, если они ограничены набором всех морфизмов, источником и целью которых является данный объект. То есть,
Точнее, учитывая моноидом ( М, •), можно построить небольшую категорию только с одним объектом и морфизмами являются элементами M. Композиция морфизмов задается операцией моноида •.
Точно так же гомоморфизмы моноидов - это просто функторы между категориями отдельных объектов. Так эта конструкция дает эквивалентность между категорией (малых) моноидах пн и полной подкатегории категории (малые) Категории Cat. Точно так же категория групп эквивалентна другой полной подкатегории Cat.
В этом смысле теорию категорий можно рассматривать как расширение концепции моноида. Многие определения и теоремы о моноидах можно обобщить на небольшие категории с более чем одним объектом. Например, частное категории с одним объектом - это просто частный моноид.
Моноиды, как и другие алгебраические структуры, также образуют свою собственную категорию Mon, объекты которой являются моноидами, а морфизмы - гомоморфизмами моноидов.
Существует также понятие моноидного объекта, которое является абстрактным определением того, что является моноидом в категории. Моноидный объект в Set - это просто моноид.
В информатике многие абстрактные типы данных могут иметь моноидную структуру. В обычном шаблоне последовательность элементов моноида « складывается » или «накапливается» для получения окончательного значения. Например, многим итеративным алгоритмам необходимо обновлять некоторую «промежуточную сумму» на каждой итерации; этот образец может быть элегантно выражен моноидной операцией. В качестве альтернативы, ассоциативность моноидных операций гарантирует, что операцию можно распараллелить, используя сумму префиксов или аналогичный алгоритм, чтобы эффективно использовать несколько ядер или процессоров.
Для данной последовательности значений типа M с элементом идентичности и ассоциативной операцией операция сворачивания определяется следующим образом:
Кроме того, любая структура данных может быть «свернута» аналогичным образом, учитывая сериализацию ее элементов. Например, результат «сворачивания» бинарного дерева может отличаться в зависимости от обхода дерева предварительного или последующего заказа.
Применение моноидов в информатике - это так называемая модель программирования MapReduce (см. Кодирование Map-Reduce как моноида с левым складыванием ). В вычислениях MapReduce состоит из двух или трех операций. Для данного набора данных «Карта» состоит из сопоставления произвольных данных с элементами определенного моноида. "Reduce" состоит из сворачивания этих элементов, так что в итоге мы получаем только один элемент.
Например, если у нас есть мультимножество, в программе оно представлено в виде карты от элементов к их номерам. Элементы в этом случае называются ключами. Количество отдельных ключей может быть слишком большим, и в этом случае мультимножество сегментируется. Чтобы правильно завершить редукцию, на этапе «Перемешивание» данные перегруппировываются между узлами. Если этот шаг нам не нужен, вся Map / Reduce состоит из сопоставления и сокращения; обе операции являются параллелизируемыми, первая из-за ее поэлементного характера, вторая из-за ассоциативности моноида.
Полная моноид является коммутативным моноид оснащен инфинитарной операцией суммы для любого индекса установлен я так, что:
а также
Непрерывный моноид является упорядоченным коммутативным моноидом, в котором каждое направленном множество имеет минимум верхней границы совместим с операцией моноидной:
Эти два понятия тесно связаны: непрерывный моноид - это полный моноид, в котором бесконечная сумма может быть определена как
где супремум справа пробегает все конечные подмножества E в I, а каждая сумма справа является конечной суммой в моноиде.