Префиксная сумма

В информатике префиксная сумма, кумулятивная сумма, включительно сканирование или просто сканирование последовательности чисел x 0, x 1, x 2,... - вторая последовательность чисел y 0, y 1, y 2,..., суммы префиксов (промежуточные суммы ) входной последовательности:

y0= x 0

y1= x 0 + x 1

y2= x 0 + x 1 + x 2

...

Например, префиксные суммы натуральных чисел являются треугольными числами :

входные числа	1	2	3	4	5	6	...
префиксные суммы	1	3	6	10	15	21	...

Префиксные суммы тривиально вычислить в последовательных моделях вычислений, используя формулу y i = y i - 1 + x i для вычисления каждого выходного значения в порядке последовательности. Однако, несмотря на простоту вычисления, префиксные суммы являются полезным примитивом в некоторых алгоритмах, таких как сортировка подсчета, и они формируют основу функции высшего порядка scan в функциональное программирование языков. Суммы префиксов также широко изучались в параллельных алгоритмах, как в качестве тестовой задачи, которая должна быть решена, так и в качестве полезного примитива для использования в качестве подпрограммы в других параллельных алгоритмах.

В абстрактном смысле, a Для суммирования префикса требуется только бинарный ассоциативный оператор ⊕, что делает его полезным для многих приложений, от вычисления разложений пар точек до обработки строк.

Математически операцию взятия префиксных сумм можно обобщить от конечных до бесконечных последовательностей; в этом контексте префиксная сумма известна как частичная сумма ряда серии. Префиксное суммирование или частичное суммирование формируют линейные операторы в векторных пространствах конечных или бесконечных последовательностей; их обратные - операторы конечных разностей.

• 1 Сканирование функции высшего порядка
  • 1.1 Инклюзивное и исключающее сканирование
• 2 Параллельные алгоритмы
  • 2.1 Алгоритм 1: Более короткий интервал, более параллельный
  • 2.2 Алгоритм 2: Эффективно с точки зрения работы
  • 2.3 Обсуждение
  • 2.4 Конкретные реализации алгоритмов суммирования префиксов
    • 2.4.1 Общая память: двухуровневый алгоритм
    • 2.4.2 Распределенная память: алгоритм гиперкуба
    • 2.4.3 Большие размеры сообщений: конвейерное двоичное дерево
      • 2.4.3.1 Конвейерная обработка
• 3 Структуры данных
• 4 Приложения
• 5 См. Также
• 6 Ссылки
• 7 Внешние ссылки

В термины функционального программирования, сумма префикса может быть обобщена для любой двоичной операции (не только для операции сложения ); функция высшего порядка, полученная в результате этого обобщения, называется сканированием, и она тесно связана с операцией свернуть. И сканирование, и операции сворачивания применяют данную бинарную операцию к одной и той же последовательности значений, но отличаются тем, что сканирование возвращает всю последовательность результатов бинарной операции, тогда как свертка возвращает только окончательный результат. Например, последовательность чисел факториала может быть сгенерирована путем сканирования натуральных чисел с использованием умножения вместо сложения:

входные числа	1	2	3	4	5	6	...
префикс продуктов	1	2	6	24	120	720	...

Инклюзивное и исключающее сканирование

Реализация сканирования на языке программирования и библиотеках может быть включающим или исключающим. Инклюзивное сканирование включает ввод x i при вычислении вывода y i (т.е. $yi\; =\; ⨁\; j\; =\; 0\; I\; xj\; \{\backslash \; displaystyle\; y\_\; \{i\}\; =\; \backslash \; bigoplus\; \_\; \{\; j\; =\; 0\}\; ^\; \{I\}\; x\_\; \{j\}\}$), а исключительное сканирование - нет (т. е. $yi\; =\; ⨁\; j\; =\; 0\; i\; -\; 1\; xj\; \{\backslash \; displaystyle\; y\_\; \{i\}\; =\; \backslash \; bigoplus\; \_\; \{j\; =\; 0\}\; ^\; \{i-1\}\; x\_\; \{j\}\}$). В последнем случае реализации либо оставляют y 0 неопределенным, либо принимают отдельное значение «x -1 », которым заполняется сканирование. Эксклюзивное сканирование является более общим в том смысле, что инклюзивное сканирование всегда может быть реализовано в терминах эксклюзивного сканирования (путем последующего объединения x i с y i), но эксклюзивное сканирование не может всегда реализовываться в терминах инклюзивного сканирования, как в случае, когда ⊕ равно max.

В следующей таблице перечислены примеры включающих и эксклюзивных функций сканирования, предоставляемых несколькими языками программирования и библиотеками:

Язык / библиотека	Инклюзивное сканирование	Исключительное сканирование
Haskell	scanl1	scanl
MPI	MPI_Scan	MPI_Exscan
C ++	std: : inclusive_scan	std :: exclusive_scan
Scala	scan
Rust	scan

Есть два ключевых алгоритма для параллельного вычисления суммы префиксов. Первый предлагает более короткий промежуток и больший параллелизм, но неэффективен для работы. Второй вариант эффективен в работе, но требует удвоения диапазона и меньшего параллелизма. Они по очереди представлены ниже.

Алгоритм 1: Более короткий промежуток, более параллельный

Представление схемы высокопараллельной суммы параллельных префиксов с 16 входами

Hillis и Steele представляют следующую сумму параллельных префиксов алгоритм:

для $i\; \leftarrow \; 0\; \{\backslash \; displaystyle\; i\; \backslash \; получает\; 0\}$to$\lceil \; log\; 2\; \; n\; \rceil \; -\; 1\; \{\backslash \; displaystyle\; \backslash \; lceil\; \backslash \; log\; \_\; \{2\}\; n\; \backslash \; rceil\; -1\; \}$do

для$j\; \leftarrow \; 0\; \{\backslash \; displaystyle\; j\; \backslash \; gets\; 0\}$to$n\; -\; 1\; \{\backslash \; displaystyle\; n-1\}$do in parallel

ifзатем

$xji\; +\; 1\; \leftarrow \; xji\; \{\backslash \; displaystyle\; x\_\; \{j\}\; ^\; \{i\; +\; 1\}\; \backslash \; получает\; x\_\; \{j\}\; ^\; \{i\}\}$

else

$xji\; +\; 1\; \leftarrow \; xji\; +\; xj\; -\; 2\; ii\; \{\backslash \; displaystyle\; x\_\; \{j\; \}\; ^\; \{i\; +\; 1\}\; \backslash \; получает\; x\_\; \{j\}\; ^\; \{i\}\; +\; x\_\; \{j-2\; ^\; \{i\}\}\; ^\; \{i\}\}$

В приведенном выше обозначении $xji\; \{\backslash \; displaystyle\; x\_\; \{j\}\; ^\; \{i\}\}$означает значение j-го элемента массива x на временном шаге i.

Учитывая n процессоров, выполняющих каждую итерацию внутреннего цикла за постоянное время, алгоритм в целом выполняется за время O (log n), то есть количество итераций внешнего цикла.

Алгоритм 2: Эффективность работы

Схематическое представление эффективной суммы параллельных префиксов с 16 входами

Эффективную сумму параллельных префиксов можно вычислить с помощью следующих шагов.

1. Вычислить суммы последовательных пар элементов, в которых первый элемент пары имеет четный индекс: z 0 = x 0 + x 1, z 1 = x 2 + x 3 и т. Д.
2. Рекурсивно вычислить сумму префиксов w 0, w 1, w 2,... последовательности z 0, z 1, z 2,...
3. Выразите каждый член конечной последовательности y 0, y 1, y 2,... как сумму до двух члены этих промежуточных последовательностей: y 0 = x 0, y 1 = z 0, y 2 = z 0 + x 2, y 3 = w 0 и т.д. После первого значения каждое последующее число y i либо копируется с позиции на половину длины последовательности w, либо предыдущее значение добавляется к одному значению в последовательности x.

Если входная последовательность имеет n шагов, то рекурсия продолжается до глубины O (log n), что также является ограничением времени параллельной работы этого алгоритма. Количество шагов алгоритма составляет O (n), и он может быть реализован на параллельной машине произвольного доступа с O (n / log n) процессорами без какого-либо асимптотического замедления путем присвоения нескольких индексов каждому процессору. в циклах алгоритма, в котором элементов больше, чем процессоров.

Обсуждение

Каждый из предыдущих алгоритмов выполняется за время O (log n). Однако в первом случае требуется ровно log 2 n шагов, а во втором - 2 log 2 n - 2 шагов. Для проиллюстрированных примеров с 16 входами алгоритм 1 является 12-сторонним параллельным (49 единиц работы, разделенных на интервал 4), в то время как алгоритм 2 является только 4-сторонним параллельным (26 единиц работы, разделенных на интервал, равный 6). Однако алгоритм 2 эффективен с точки зрения работы - он выполняет только постоянный коэффициент (2) объема работы, требуемой последовательным алгоритмом - в то время как алгоритм 1 работает неэффективно - он выполняет асимптотически больше работы (логарифмический коэффициент), чем требуется. последовательно. Следовательно, алгоритм 1, вероятно, будет работать лучше, когда доступен обширный параллелизм, но алгоритм 2, вероятно, будет работать лучше, когда параллелизм более ограничен.

Параллельные алгоритмы для суммирования префиксов часто можно обобщить для других операций сканирования на ассоциативных двоичных операциях, а также они могут быть эффективно вычислены на современном параллельном оборудовании, таком как GPU. Идея создания аппаратного функционального блока, предназначенного для вычисления многопараметрической префиксной суммы, была запатентована Узи Вишкин.

Многие параллельные реализации следуют двухпроходной процедуре, при которой частичные префиксные суммы вычисляются на первом проходе при каждой обработке Ед. изм; затем вычисляется префиксная сумма этих частичных сумм и передается обратно в блоки обработки для второго прохода с использованием теперь известного префикса в качестве начального значения. Асимптотически этот метод требует примерно двух операций чтения и одной операции записи для каждого элемента.

Конкретные реализации алгоритмов суммы префиксов

Реализация параллельного алгоритма суммы префиксов, как и другие параллельные алгоритмы, должна учитывать архитектуру распараллеливания платформы. В частности, существует несколько алгоритмов, адаптированных для платформ, работающих с общей памятью, а также алгоритмов, которые хорошо подходят для платформ, использующих распределенную память, полагаясь на передачу сообщений как единственная форма межпроцессного взаимодействия.

Общая память: двухуровневый алгоритм

Следующий алгоритм предполагает модель машины с общей памятью ; все элементы обработки (PE) имеют доступ к одной и той же памяти. Версия этого алгоритма реализована в многоядерной стандартной библиотеке шаблонов (MCSTL), параллельной реализации стандартной библиотеки шаблонов C ++, которая предоставляет адаптированные версии для параллельных вычислений различных алгоритмов.

Для одновременного вычисления суммы префиксов по $n\; \{\backslash \; displaystyle\; n\}$элементам данных с $p\; \{\backslash \; displaystyle\; p\}$элементами обработки данные делятся на $p\; +\; 1\; \{\backslash \; displaystyle\; p\; +\; 1\}$блоки, каждый из которых содержит $np\; +\; 1\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{n\}\; \{p\; +\; 1\}\}\; \}$элементы (для простоты мы предполагаем, что $p\; +\; 1\; \{\backslash \; displaystyle\; p\; +\; 1\}$делит $n\; \{\backslash \; displaystyle\; n\}$). Обратите внимание, что хотя алгоритм делит данные на блоки $p\; +\; 1\; \{\backslash \; displaystyle\; p\; +\; 1\}$, выполняются только элементы обработки $p\; \{\backslash \; displaystyle\; p\}$параллельно за раз.

В первом цикле каждый PE вычисляет локальную сумму префиксов для своего блока. Последний блок вычислять не нужно, поскольку эти суммы префиксов рассчитываются только как смещения к суммам префиксов последующих блоков, а последний блок по определению не выполняется.

Смещения $p\; \{\backslash \; displaystyle\; p\}$, которые хранятся в последней позиции каждого блока, накапливаются в собственной сумме префиксов и сохраняются в своих последующих позициях. Если $p\; \{\backslash \; displaystyle\; p\}$- небольшое число, быстрее делать это последовательно, для большого $p\; \{\backslash \; displaystyle\; p\}$этот шаг можно было бы сделать параллельно.

Выполняется вторая развертка. На этот раз первый блок не нужно обрабатывать, так как не нужно учитывать смещение предыдущего блока. Однако в этот цикл вместо него включается последний блок, и суммы префиксов для каждого блока вычисляются с учетом смещений блоков суммы префиксов, вычисленных в предыдущем цикле.

function prefix_sum (elements) {n: = size (elements) p: = number of processing elements prefix_sum: = [0... 0] of size n do parallel i = 0 to p-1 {// i: = индекс текущего PE от j = i * n / (p + 1) до (i + 1) * n / (p + 1) - 1 do {// Сохраняет только префиксную сумму локальных блоков store_prefix_sum_with_offset_in (elements, 0, prefix_sum)}} x = 0 для i = 1 to p {x + = prefix_sum [i * n / (p + 1) - 1] // Построение суммы префикса по первым p блокам prefix_sum [i * n / (p + 1)] = x // Сохраняем результаты для использования в качестве смещений во второй развертке} do parallel i = 1 to p {// i: = index of current PE from j = i * n / (p + 1) to (i + 1) * n / (p + 1) - 1 do {offset: = prefix_sum [i * n / (p + 1)] // Вычислить сумму префикса, взяв сумму предыдущих блоков как смещение store_prefix_sum_with_offset_in (elements, offset, prefix_sum)}} return prefix_sum}

Распределенная память: алгоритм гиперкуба

Алгоритм суммы префиксов гиперкуба хорошо адаптирован для платформ с распределенной памятью и других платформ. ks с обменом сообщениями между элементами обработки. Предполагается, что $p\; =\; 2\; d\; \{\backslash \; displaystyle\; p\; =\; 2\; ^\; \{d\}\}$процессорных элементов (PE), участвующих в алгоритме, равно количеству углов в $d\; \{\; \backslash \; displaystyle\; d\}$-мерный гиперкуб.

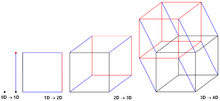Различные гиперкубы для разного количества узлов

На протяжении всего алгоритма каждый PE рассматривается как угол в гипотетическом гиперкубе, при этом известно общее сумма префикса $\sigma \; \{\backslash \; displaystyle\; \backslash \; sigma\}$, а также сумма префикса $x\; \{\backslash \; displaystyle\; x\}$всех элементов до самого себя (согласно упорядоченному индексы среди PE), оба в своем гиперкубе.

• Алгоритм начинается с предположения, что каждый PE является единственным углом нульмерного гиперкуба и, следовательно, $\sigma \; \{\backslash \; displaystyle\; \backslash \; sigma\}$и $x\; \{\backslash \; displaystyle\; x\}$равны локальной сумме префиксов своих собственных элементов.
• Алгоритм продолжается путем объединения гиперкубов, которые смежны по одному измерению. Во время каждого объединения $\sigma \; \{\backslash \; displaystyle\; \backslash \; sigma\}$обменивается и агрегируется между двумя гиперкубами, что сохраняет неизменным тот факт, что все PE в углах этого нового гиперкуба хранят общую сумму префиксов этого новый унифицированный гиперкуб в их переменной $\sigma \; \{\backslash \; displaystyle\; \backslash \; sigma\}$. Однако только гиперкуб, содержащий PE с более высоким индексом, также добавляет этот $\sigma \; \{\backslash \; displaystyle\; \backslash \; sigma\}$к их локальной переменной $x\; \{\backslash \; displaystyle\; x\}$с сохранением инварианта, что $x\; \{\backslash \; displaystyle\; x\}$хранит только значение суммы префиксов всех элементов в PE с индексами, меньшими или равными их собственному индексу.

В $d\; \{\backslash \; displaystyle\; d\}$-мерный гиперкуб с $2\; d\; \{\backslash \; displaystyle\; 2\; ^\; \{d\}\}$PE по углам, алгоритм необходимо повторить $d\; \{\backslash \; displaystyle\; d\}$раз, чтобы $2\; d\; \{\backslash \; displaystyle\; 2\; ^\; \{d\}\}$нульмерные гиперкубы были объединены в один $d\; \{\backslash \; displaystyle\; d\}$-мерный гиперкуб. Если предположить, что модель дуплексной связи , где $\sigma \; \{\backslash \; displaystyle\; \backslash \; sigma\}$двух соседних PE в разных гиперкубах может обмениваться в обоих направлениях за один этап связи, это означает $d\; =\; log\; 2\; \; p\; \{\backslash \; displaystyle\; d\; =\; \backslash \; log\; \_\; \{2\}\; p\}$запусков связи.

i: = Индекс собственного процессорного элемента (PE) m: = префиксная сумма локальных элементов этого PE d: = количество измерений гиперкуба x = m; // Инвариант: Сумма префикса для этого PE в текущем субкубе σ = m; // Инвариант: префиксная сумма всех элементов в текущем субкубе для (k = 0; k <= d-1; k++) { y = σ @ PE(i xor 2^k) // Get the total prefix sum of the opposing sub cube along dimension k σ = σ + y // Aggregate the prefix sum of both sub cubes if (i 2^k) { x = x + y // Only aggregate the prefix sum from the other sub cube, if this PE is the higher index one. } }

Большие размеры сообщений: конвейерное двоичное дерево

Конвейерный алгоритм двоичного дерева - еще один алгоритм для платформ с распределенной памятью который особенно хорошо подходит для сообщений большого размера.

Как и алгоритм гиперкуба, он предполагает особую структуру связи. Элементы обработки (PE) гипотетически расположены в виде двоичного дерева (например, Дерево Фибоначчи) с инфиксной нумерацией в соответствии с их индексом в PE. Связь в таком дереве всегда происходит между родительскими и дочерними узлами.

инфиксная нумерация гарантирует, что для любого заданного PE j, индексы всех узлов, достижимых его левым поддеревом $[l...\; j\; -\; 1]\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{[l...\; j-1]\}\; \}$меньше $j\; \{\backslash \; displaystyle\; j\}$и индексы $[j\; +\; 1...\; r]\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{[j\; +\; 1...\; r]\}\}$всех узлов в правом поддереве ar е больше, чем $j\; \{\backslash \; displaystyle\; j\}$. Индекс родительского элемента больше любого из индексов в поддереве PE j, если PE j является левым дочерним элементом, и меньше, если PE j является правым дочерним элементом. Это дает основание для следующих рассуждений:

Обмен информацией между обрабатывающими элементами во время восходящей (синий) и нисходящей (красный) фаз в алгоритме конвейерной суммы префиксов двоичного дерева.

• Локальная сумма префиксов $\oplus \; [l..\; j\; -\; 1]\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{\backslash \; oplus\; [l..j-1]\}\}$левого поддерева необходимо агрегировать для вычисления локального префикса PE j сумма $\oplus \; [л..\; j]\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{\backslash \; oplus\; [l..j]\}\}$.
• Сумма местного префикса $\oplus \; [j\; +\; 1..\; r]\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{\backslash \; oplus\; [j\; +\; 1..r]\}\}$правого поддерева необходимо агрегировать для вычисления локальной суммы префиксов PE более высокого уровня h, которые достигаются на пути, содержащем левое дочернее соединение (что означает $h>j\; \{\backslash \; displaystyle\; h>j\}$).
• Общая сумма префиксов $\oplus \; [0..\; j]\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{\backslash \; oplus\; [0..j]\}\}$из PE j необходимо для вычисления общих сумм префиксов в правом поддереве (например, $\oplus \; [0..\; j.\; R]\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{\backslash \; oplus\; [0..j..r]\}\}$для узла с наивысшим индексом в поддереве).
• PEjдолжен включать общую сумму префиксов $\oplus \; [0..\; l\; -\; 1]\; \{\; \backslash \; displaystyle\; \backslash \; mathbb\; \{\backslash \; oplus\; [0..l-1]\}\}$первого узла более высокого порядка, который достигается через восходящий путь, включающий правильное дочернее соединение для вычисления его общей суммы префиксов.

Обратите внимание на различие между суммой локального поддерева и общей суммой префиксов. Точки два, три и четыре могут наводить на мысль, что они образуют круговую зависимость, но это не так. PE более низкого уровня могут потребовать общую сумму префиксов PE более высокого уровня для вычисления их общей суммы префиксов, но PE более высокого уровня требуют только суммы локальных префиксов поддерева для вычисления их общей суммы префиксов. Корневому узлу как узлу самого высокого уровня требуется только локальная сумма префиксов его левого поддерева для вычисления своей собственной суммы префиксов. Каждому PE на пути от PE 0 к корневому PE требуется только локальная сумма префиксов его левого поддерева для вычисления своей собственной суммы префиксов, тогда как каждый узел на пути от PE p-1 (последний PE) к PE корень требует, чтобы общая сумма префиксов его родительского элемента вычислялась его собственной общей суммой префиксов.

Это приводит к двухфазному алгоритму:

восходящая фаза . Распространение локальной префиксной суммы поддерева $\oplus \; [l..\; j..\; r]\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{\backslash \; oplus\; [l..j..r]\}\}$своему родительскому элементу для каждого PE j.

Нисходящая фаза . Распространение эксклюзивного (эксклюзивного PE j, а также PE в его левом поддереве) общая сумма префиксов $\oplus \; [0..\; l\; -\; 1]\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{\backslash \; oplus\; [0..l-1]\}\}$всех PE нижнего индекса, которые не включены в адресуемое поддерево PE j, до PE нижнего уровня в левом дочернем поддереве PE j. Распространите включающую префиксную сумму $\oplus \; [0..\; j]\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{\backslash \; oplus\; [0..j]\}\}$в правое дочернее поддерево PE j.

Обратите внимание, что Алгоритм выполняется параллельно на каждом PE, и PE будут блокироваться при получении, пока их дети / родители не предоставят им пакеты.

k: = количество пакетов в сообщении m PE m @ {left, right, parent, this}: = // Сообщения в разных PE x = m @ this // Фаза вверх - вычисление локального префикса поддерева суммы от j = 0 до k-1: // Конвейерная обработка: для каждого пакета сообщения, если hasLeftChild: блокирование приема m [j] @ left // Это заменяет локальный m [j] полученным m [j] // Агрегировать включающую локальную сумму префиксов из PE с нижним индексом x [j] = m [j] ⨁ x [j] if hasRightChild: блокирующий прием m [j] @ right // Мы не агрегируем m [j] в локальную сумму префиксов, поскольку правые дочерние элементы имеют более высокий индекс PE, отправьте x [j] ⨁ m [j] родительскому элементу else: отправьте x [j] родительскому элементу // Нисходящая фаза для j = 0 до k-1: m [j] @ this = 0 if hasParent: blocking receive m [j] @ parent // Для левого потомка m [j] - это исключающая сумма префикса родителей, для правого потомка - включающая префиксная сумма x [j] = m [j] ⨁ x [j] send m [j] to left // Общая сумма префиксов всех PE, меньших этого или любого PE в левом поддереве send x [j] вправо // Общая сумма префиксов всех PE меньше или равен этому PE

Конвейерная обработка

Если сообщение $m\; \{\backslash \; displaystyle\; m\}$длины $n\; \{\backslash \; displaystyle\; n\}$можно разделить на $k\; \{\backslash \; displaystyle\; k\}$пакеты, а оператор ⨁ можно использовать для каждого из соответствующих пакетов сообщений отдельно, конвейерная обработка возможна.

Если алгоритм используется без конвейерной обработки, всегда работают только два уровня (отправляющие PE и принимающие PE) двоичного дерева, в то время как все остальные PE ожидают. Если есть элементы обработки $p\; \{\backslash \; displaystyle\; p\}$и используется сбалансированное двоичное дерево, дерево имеет $log\; 2\; \; p\; \{\backslash \; displaystyle\; \backslash \; log\; \_\; \{2\}\; p\}$уровней, длина пути от $PE\; 0\; \{\backslash \; displaystyle\; PE\_\; \{0\}\}$до $PE\; root\; \{\backslash \; displaystyle\; PE\; \_\; \{\backslash \; mathbb\; \{root\}\}\}$, следовательно, $log\; 2\; \; p\; -\; 1\; \{\backslash \; displaystyle\; \backslash \; log\; \_\; \{2\}\; p-1\}$, который представляет максимальное количество непараллельных коммуникационных операций во время восходящей фазы., аналогично, связь по нисходящему пути также ограничена $log\; 2\; \; p\; -\; 1\; \{\backslash \; displaystyle\; \backslash \; log\; \_\; \{2\}\; p-1\}$запусками. Предполагая, что время запуска связи составляет $T\; start\; \{\backslash \; displaystyle\; T\; \_\; \{\backslash \; mathbb\; \{start\}\}\}$и время побайтной передачи составляет $T\; byte\; \{\backslash \; displaystyle\; T\; \_\; \{\backslash \; mathbb\; \{byte\}\; \}\}$, восходящая и нисходящая фазы ограничены $(2\; log\; 2\; \; p\; -\; 2)\; (T\; start\; +\; n\; \ast \; T\; byte)\; \{\backslash \; displaystyle\; (2\; \backslash \; log\; \_\; \{2\}\; p-\; 2)\; (T\; \_\; \{\backslash \; mathbb\; \{start\}\}\; +\; n\; *\; T\; \_\; \{\backslash \; mathbb\; \{byte\}\})\}$в неконвейерном сценарии.

После разделения на k пакетов, каждый размером $nk\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{n\}\; \{k\}\}\}$и их отправки по отдельности, для первого пакета по-прежнему требуется $(журнал\; 2\; \; п\; -\; 1)\; (T\; начало\; +\; nk\; *\; T\; байт)\; \{\backslash \; displaystyle\; (\backslash \; log\; \_\; \{2\}\; p-1)\; (T\; \_\; \{\backslash \; mathbb\; \{start\}\}\; +\; \{\backslash \; frac\; \{n\}\; \{\; k\}\}\; *\; T\; \_\; \{\backslash \; mathbb\; \{byte\}\})\}$для распространения на $корень\; PE\; \{\backslash \; displaystyle\; PE\; \_\; \{\backslash \; mathbb\; \{root\}\}\}$как часть сумма локального префикса, и это произойдет снова для последнего пакета, если $k>log\; 2\; \; p\; \{\backslash \; displaystyle\; k>\backslash \; log\; \_\; \{2\}\; p\}$. Однако между ними все PE вдоль пути может работать параллельно, и каждая третья операция связи (прием слева, прием справа, отправка родительскому) отправляет пакет на следующий уровень, так что одна фаза может быть завершена за $2\; log\; 2\; \; p\; -\; 1\; +\; 3\; (к\; -\; 1)\; \{\backslash \; displaystyle\; 2\; \backslash \; log\; \_\; \{2\}\; p-1\; +\; 3\; (k-1)\}$связь Для операций объединения и обеих фаз вместе требуется $(4\; \ast \; log\; 2\; \; p\; -\; 2\; +\; 6\; (k\; -\; 1))\; (T\; start\; +\; nk\; \ast \; T\; byte)\; \{\backslash \; displaystyle\; (4\; *\; \backslash \; log\; \_\; \{2\}\; p-\; 2\; +\; 6\; (k-1))\; (T\; \_\; \{\backslash \; mathbb\; \{start\}\}\; +\; \{\backslash \; frac\; \{n\}\; \{k\}\}\; *\; T\; \_\; \{\backslash \; mathbb\; \{byte\}\})\}$что благоприятно для большие размеры сообщений $n\; \{\backslash \; displaystyle\; n\}$.

Алгоритм можно дополнительно оптимизировать, используя полнодуплексную связь или связь по модели телефона и перекрывая восходящую и нисходящую фазы.

Когда набор данных может обновляться динамически, он может храниться в структуре данных дерево Фенвика. Эта структура позволяет как искать любое индивидуальное значение суммы префикса, так и изменять любое значение массива за логарифмическое время за операцию. Однако в более ранней статье 1982 г. представлена ​​структура данных, называемая деревом частичных сумм (см. Раздел 5.1), которая, по-видимому, перекрывает деревья Фенвика; в 1982 году термин «префикс-сумма» еще не был так распространен, как сегодня.

Для многомерных массивов таблица суммированных областей обеспечивает структуру данных на основе сумм префиксов для вычисления сумм произвольных прямоугольных подмассивов. Это может быть полезным примитивом в операциях свертки изображений.

Counting sort - это алгоритм целочисленной сортировки, который использует сумму префиксов гистограмма частот клавиш для вычисления позиции каждого ключа в отсортированном выходном массиве. Он работает за линейное время для целочисленных ключей, размер которых меньше количества элементов, и часто используется как часть radix sort, быстрого алгоритма сортировки целых чисел, размер которых менее ограничен.

Список ранжирование, проблема преобразования связанного списка в массив, представляющий ту же последовательность элементов, может рассматриваться как вычисление суммы префикса для последовательности 1, 1, 1,... и затем сопоставление каждого элемента с позицией массива, заданной его значением суммы префикса; за счет объединения ранжирования списков, сумм префиксов и обходов Эйлера многие важные проблемы на деревьях могут быть решены с помощью эффективных параллельных алгоритмов.

Раннее применение параллельной суммы префиксов Алгоритмы были разработаны в виде двоичных сумматоров, логических схем, которые могут складывать два n-битных двоичных числа. В этом приложении последовательность битов переноса сложения может быть представлена ​​как операция сканирования последовательности пар входных битов с использованием функции большинства для объединения предыдущего переноса с этими двумя битами. Каждый бит выходного номера затем может быть найден как исключающий или из двух входных битов с соответствующим битом переноса. Используя схему, которая выполняет операции параллельного алгоритма суммирования префиксов, можно разработать сумматор, который использует O (n) логических вентилей и O (log n) временных шагов.

В Параллельная машина с произвольным доступом модель вычислений, префиксные суммы могут использоваться для моделирования параллельных алгоритмов, которые предполагают возможность одновременного доступа нескольких процессоров к одной и той же ячейке памяти на параллельных машинах, которые запрещают одновременный доступ. Посредством сети сортировки набор параллельных запросов доступа к памяти может быть упорядочен в последовательность, так что доступы к одной и той же ячейке будут непрерывными в пределах последовательности; Затем операции сканирования могут использоваться для определения того, какой из обращений успешно записывает в запрошенные ячейки, и для распределения результатов операций чтения из памяти на несколько процессоров, которые запрашивают один и тот же результат.

В Guy Blelloch доктор философии. Согласно утверждению, параллельные операции с префиксом являются частью формализации модели параллелизма данных, предоставляемой такими машинами, как Connection Machine. Машина соединений CM-1 и CM-2 обеспечивала гиперкубическую сеть, в которой мог быть реализован описанный выше алгоритм 1, тогда как CM-5 предоставлял выделенную сеть для реализации алгоритма 2.

При построении кодов Грея последовательностей двоичных значений со свойством, что значения последовательных последовательностей отличаются друг от друга в одной битовой позиции, число n может быть преобразовано в значение кода Грея в позиции n последовательность, просто взяв исключающее или из n и n / 2 (число, образованное сдвигом n вправо на одну битовую позицию). Обратная операция - декодирование значения x, закодированного по Грею, в двоичное число - более сложна, но может быть выражена как сумма префиксов битов x, где каждая операция суммирования в пределах суммы префикса выполняется по модулю два. Сумма префиксов этого типа может быть эффективно выполнена с использованием побитовых логических операций, доступных на современных компьютерах, путем вычисления исключающего или числа x с каждым из чисел, образованных сдвигом x влево на некоторое количество битов. это степень двойки.

Параллельный префикс (с использованием умножения в качестве базовой ассоциативной операции) также может использоваться для построения быстрых алгоритмов параллельной полиномиальной интерполяции. В частности, его можно использовать для вычисления коэффициентов разделенной разности формы Ньютона полинома интерполяции. Этот подход на основе префиксов также можно использовать для получения обобщенных разделенных разностей для (конфлюэнтной) интерполяции Эрмита, а также для параллельных алгоритмов для систем Вандермонда.

• Универсальные вычисления на графических процессорах

• Вайсштейн, Эрик У. «Совокупная сумма». MathWorld.