Коммутативное кольцо

Алгебраическая структура

В теории колец, ветви абстрактной алгебры, коммутативное кольцо - это кольцо, в котором операция умножения коммутативна. Изучение коммутативных колец называется коммутативной алгеброй. Кроме того, некоммутативная алгебра - это исследование некоммутативных колец, где умножение не обязательно должно быть коммутативным.

• 1 Определение и первые примеры
  • 1.1 Определение
  • 1.2 Первые примеры
• 2 Делимость
  • 2.1 Локализации
• 3 Идеалы и модули
  • 3.1 Модули и идеалы
  • 3.2 Идеалы
    • 3.2.1 Области главных идеалов
    • 3.2.2 Фактор-кольцо
  • 3.3 Нётеровы кольца
  • 3.4 Артиновы кольца
• 4 Спектр коммутативного кольца
  • 4.1 Простые идеалы
  • 4.2 Спектр
  • 4.3 Аффинные схемы
  • 4.4 Размерность
• 5 Гомоморфизмы колец
  • 5.1 Конечное поколение
• 6 Локальные кольца
  • 6.1 Правильные локальные кольца
  • 6.2 Полные пересечения
  • 6.3 Кольца Коэна – Маколея
• 7 Построение коммутативных колец
  • 7.1 Пополнения
• 8 Гомологические понятия
  • 8.1 Проективные модули и Ext-функторы
  • 8.2 Плоскостность
• 9 Свойства
• 10 Обобщения
  • 10.1 Градиентно-коммутативные кольца
  • 10.2 Симплициальные коммутативные кольца
• 11 См. Также
• 12 Примечания
  • 12.1 Цитаты
• 13 Ссылки

Определение

Кольцо - это набор R снабжен двумя бинарными операциями , то есть операциями, объединяющими любые два элемента кольца в третий. Они называются сложением и умножением и обычно обозначаются «+» и «⋅»; например a + b и a ⋅ b. Чтобы сформировать кольцо, эти две операции должны удовлетворять ряду свойств: кольцо должно быть абелевой группой при сложении, а также моноидом при умножении, где умножение распределяет сверх сложения; т.е. a ⋅ (b + c) = (a ⋅ b) + (a ⋅ c). Единичные элементы для сложения и умножения обозначаются 0 и 1 соответственно.

Если умножение коммутативное, т.е.

a ⋅ b = b ⋅ a,

, то кольцо R называется коммутативным. В оставшейся части статьи все кольца будут коммутативными, если явно не указано иное.

Первые примеры

Важным и в некотором смысле решающим примером является кольцо целых чисел Zс двумя операциями сложения и умножения. Поскольку умножение целых чисел - это коммутативная операция, это коммутативное кольцо. Обычно обозначается Z как сокращение от немецкого слова Zahlen (числа).

A поле - коммутативное кольцо, где $0\; \ne \; 1\; \{\backslash \; displaystyle\; 0\; \backslash \; not\; =\; 1\}$и каждый ненулевой элемент a является обратимым; т.е. имеет мультипликативный обратный элемент b такой, что a ⋅ b = 1. Следовательно, по определению, любое поле является коммутативным кольцом. Поля формы рациональное, действительное и комплексное число.

Если R - данное коммутативное кольцо, то набор всех многочленов от переменной X, коэффициенты которой находятся в R, образует кольцо многочленов, обозначенное R [X ]. То же самое верно для нескольких переменных.

Если V является некоторым топологическим пространством, например, подмножеством некоторых R, действительных или комплексных непрерывных функций в форме V коммутативное кольцо. То же самое верно для дифференцируемых или голоморфных функций, когда определены два понятия, например, для V a комплексное многообразие.

In в отличие от полей, где каждый ненулевой элемент мультипликативно обратим, концепция делимости для колец богаче. Элемент a кольца R называется блоком , если он обладает мультипликативным обратным. Другой конкретный тип элементов - это делители нуля, то есть элемент a такой, что существует ненулевой элемент b кольца такой, что ab = 0. Если R не имеет ненулевых делителей нуля, он называется областью целостности (или областью). Элемент a, удовлетворяющий a = 0 для некоторого положительного целого числа n, называется нильпотентным.

Локализацией

Локализация кольца - это процесс, в котором некоторые элементы становятся обратимыми, т. Е. К ним добавляются мультипликативные обратные кольцо. Конкретно, если S является мультипликативно замкнутым подмножеством в R (т. Е. Всякий раз, когда s, t ∈ S, то так и является st), то локализация R в S или кольце дробей со знаменателями в S, обычно обозначаемая SR состоит из символов

$rs\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{r\}\; \{s\}\}\}$с r ∈ R, s ∈ S

с соблюдением определенных правил, имитирующих сокращение, знакомое по рациональным числам. Действительно, на этом языке Q - это локализация Z для всех ненулевых целых чисел. Эта конструкция работает для любой области целостности R вместо Z . Локализация (R \ {0}) R - это поле, называемое полем частных R.

Многие из следующих понятий также существуют для не обязательно коммутативные кольца, но определения и свойства обычно более сложны. Например, все идеалы в коммутативном кольце автоматически двусторонние, что значительно упрощает ситуацию.

Модули и идеалы

Для кольца R R-модуль M подобен тому, что векторное пространство для поля. То есть можно добавлять элементы в модуль; они могут быть умножены на элементы R с соблюдением тех же аксиом, что и для векторного пространства. Изучение модулей значительно сложнее, чем изучение векторных пространств в линейной алгебре , поскольку некоторые особенности векторных пространств не подходят для модулей в целом: модули не обязательно должны быть свободными, т. Е. вида

$M\; =\; ⨁\; i\; \in \; IR.\; \{\backslash \; displaystyle\; M\; =\; \backslash \; bigoplus\; \_\; \{i\; \backslash \; in\; I\}\; R.\}$

Даже для бесплатных модулей ранг свободного модуля (т. е. аналог размерности векторных пространств) не может быть четко определенным. Наконец, подмодули конечно порожденных модулей не обязательно должны быть конечно порожденными (если R не является нётеровым, см. ниже).

Идеалы

Идеалы кольца R - это подмодули в R, то есть модули, содержащиеся в R. Более подробно, идеал I является непустым подмножество R такое, что для всех r в R, i и j в I, как ri, так и i + j находятся в I. Для различных приложений понимание идеалов кольца имеет особое значение, но часто следует изучать модули в Генеральная.

Любое кольцо имеет два идеала, а именно нулевой идеал {0} и R, все кольцо. Эти два идеала - единственные в точности, если R - поле. Для любого подмножества F = {f j}j ∈ J в R (где J - некоторое множество индексов) идеал, порожденный F, является наименьшим идеалом, содержащим F. Точно так же он задается конечным линейные комбинации

r1f1+ r 2f2+... + r nfn.

Области главных идеалов

Если F состоит из одного элемента r, идеал, порожденный F, состоит из кратных r, т. е., элементы вида rs для произвольных элементов s. Такой идеал называется главным идеалом. Если каждый идеал является главным идеалом, R называется кольцом главных идеалов ; два важных случая - это Z и k [X], кольцо многочленов над полем k. Эти два являются дополнительными областями, поэтому они называются областями главных идеалов.

В отличие от общих колец, для области главных идеалов свойства отдельных элементов сильно привязаны к свойствам кольца в целом. Например, любая область главного идеала R является областью уникальной факторизации (UFD), что означает, что любой элемент является продуктом неприводимых элементов уникальным (с точностью до переупорядочения факторов) способом. Здесь элемент a в домене называется неприводимым, если единственный способ выразить его как продукт

a = bc,

состоит в том, чтобы либо b, либо c были единицей. Примером, важным в теории поля, являются неприводимые многочлены, то есть неприводимые элементы в k [X] для поля k. Тот факт, что Z является UFD, можно сформулировать более элементарно, сказав, что любое натуральное число может быть однозначно разложено как произведение степеней простых чисел. Она также известна как фундаментальная теорема арифметики.

Элемент a является простым элементом, если всякий раз, когда a делит произведение bc, a делит b или c. В области простота означает неприводимость. Обратное верно в уникальной области факторизации, но неверно в целом.

Фактор-кольцо

Определение идеалов таково, что "деление" I на "дает другое кольцо, фактор-кольцо R / I: это набор смежных классов I вместе с операциями

(a + I) + (b + I) = (a + b) + I и (a + I) (b + I) = ab + I.

Для Например, кольцо Z/nZ(также обозначается Zn), где n - целое число, представляет собой кольцо целых чисел по модулю n. Это основа модульной арифметики.

Идеал считается правильным, если он строго меньше всего кольца. Идеал, который не содержится строго ни в одном собственном идеале, называется максимальным. Идеал m максимален тогда и только тогда, когда R / m является полем. За исключением нулевого кольца, любое кольцо (с идентичностью) обладает по крайней мере одним максимальным идеалом; это следует из леммы Цорна.

Нётеровых колец

Кольцо называется нётеровым (в честь Эмми Нётер, которая разработала эту концепцию), если каждая восходящая цепочка идеалы

0 ⊆ I 0 ⊆ I 1... ⊆ I n ⊆ I n + 1 ⊆...

становится стационарным, т.е. становится постоянным после некоторого индекса n. Эквивалентно, любой идеал порождается конечным числом элементов или, что эквивалентно, подмодули конечно порожденных модулей конечно порождены.

Нётеровость является очень важным условием конечности, и это условие сохраняется при многих операциях, которые часто встречаются в геометрии. Например, если R нетерово, то и кольцо многочленов R [X 1, X 2,..., X n ] (по теорема о базисе Гильберта ), любая локализация SR, а также любое фактор-кольцо R / I.

Любое нётерово кольцо R является объединением своих нётеровых подколец. Этот факт, известный как, позволяет распространить некоторые теоремы на нётеровы кольца.

Артинианские кольца

Кольцо называется Артинианом (после Эмиля Артина ), если каждая нисходящая цепочка идеалов

R ⊇ I 0 ⊇ I 1... ⊇ I n ⊇ I n + 1 ⊇...

со временем становится стационарным. Несмотря на то, что два условия кажутся симметричными, нётеровы кольца гораздо более общие, чем артиновы кольца. Например, Z является нётеровым, поскольку каждый идеал может быть порожден одним элементом, но не артиновым, поскольку цепочка

Z⊋ 2 Z ⊋ 4 Z ⊋ 8 Z ⊋...

показывает. Фактически, согласно теореме Хопкинса – Левицки каждое артиново кольцо является нётеровым. Точнее, артиновы кольца можно охарактеризовать как нётеровы кольца, размерность Крулля которых равна нулю.

Простые идеалы

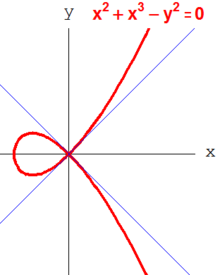
Как упоминалось выше, Z является областью уникальной факторизации. Это не верно для более общих колец, как это поняли алгебраисты в 19 веке. Например, в

$Z\; [-\; 5],\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{Z\}\; [\{\backslash \; sqrt\; \{-5\}\}],\}$

есть два совершенно разных способа записать 6 как продукт:

$6\; =\; 2\; \cdot \; 3\; =\; (1\; +\; -\; 5)\; (1\; -\; -\; 5).\; \{\backslash \; displaystyle\; 6\; =\; 2\; \backslash \; cdot\; 3\; =\; (1\; +\; \{\backslash \; sqrt\; \{-5\}\})\; (1\; -\; \{\backslash \; sqrt\; \{-5\}\}).\}$

Простые идеалы, в отличие от простых элементов, обеспечивают способ обойти эту проблему. Первичный идеал - это собственный (т.е. строго содержащийся в R) идеал p такой, что всякий раз, когда произведение ab любых двух кольцевых элементов a и b находится в p, по крайней мере, один из двух элементов уже находится в p. (Противоположный вывод верен для любого идеала по определению). Таким образом, если простой идеал является главным, он эквивалентно порождается простым элементом. Однако в таких кольцах, как $Z\; [-\; 5]\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{Z\}\; [\{\backslash \; sqrt\; \{-5\}\}]\}$, простые идеалы не обязательно должны быть главными. Это ограничивает использование простых элементов в теории колец. Однако краеугольным камнем теории алгебраических чисел является тот факт, что в любом кольце Дедекинда (которое включает $Z\; [-\; 5]\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{Z\}\; [\{\backslash \; sqrt\; \{-5\}\; \}]\}$и, в более общем смысле, кольцо целых чисел в числовом поле ) любой идеал (например, порожденный 6) однозначно разлагается как произведение простых идеалов.

Любой максимальный идеал является первичным идеалом или, короче, первичным. Более того, идеал I прост тогда и только тогда, когда фактор-кольцо R / I является областью целостности. Доказать, что идеал простой или, что то же самое, что кольцо не имеет делителей нуля, может быть очень сложно. Еще один способ выразить то же самое - сказать, что дополнение R \ p мультипликативно замкнуто. Локализация (R \ p) R достаточно важна для того, чтобы иметь свою собственную нотацию: R p. Это кольцо имеет только один максимальный идеал, а именно pR p. Такие кольца называются локальными.

Спектр

Spec (Z ) содержит точку нулевого идеала. Замыкание этой точки - все пространство. Остальные точки соответствуют идеалам (p), где p - простое число. Эти точки замкнуты.

Спектр кольца R, обозначаемый Spec R, представляет собой набор всех первичных идеалов кольца R. Он снабжен топологией топологией Зарисского, которая отражает алгебраические свойства R: базис открытых подмножеств задается формулой

D (f) = {p ∈ Spec R, f ∉ p}, где f - любой элемент кольца.

Интерпретация f как функции, которая принимает значение f mod p (т. е. образ f в поле вычетов R / p), это подмножество является локусом, где f не равно нулю. Спектр также уточняет интуицию, что локализация и фактор-кольца дополняют друг друга: естественные отображения R → R f и R → R / fR соответствуют, после наделения спектров рассматриваемых колец их топологией Зарисского, к дополнительным открытым и закрытым погружениям соответственно. Даже для основных колец, таких как показано для R = Z справа, топология Зарисского сильно отличается от топологии на множестве действительных чисел.

Спектр содержит набор максимальных идеалов, который иногда обозначают mSpec (R). Для алгебраически замкнутого поля k, mSpec (k [T 1,..., T n ] / (f 1,..., f m)) находится в биекции с множеством

{x = (x 1,..., x n) ∊ k | f 1 (x) =... = f m (x) = 0.}

Таким образом, максимальные идеалы отражают геометрические свойства множеств решений многочленов, что является исходная мотивация для изучения коммутативных колец. Однако рассмотрение немаксимальных идеалов как части геометрических свойств кольца полезно по нескольким причинам. Например, минимальные простые идеалы (то есть те, которые строго не содержат меньшие) соответствуют неприводимым компонентам Spec R. Для нётерова кольца R Spec R имеет только конечное число неприводимых компонент. Это геометрическое повторение первичной декомпозиции, согласно которой любой идеал может быть разложен как произведение конечного числа первичных идеалов. Этот факт является окончательным обобщением разложения на простые идеалы в дедекиндовом кольце.

Аффинные схемы

Понятие спектра является общей основой коммутативной алгебры и алгебраической геометрии. Алгебраическая геометрия продолжается путем наделения Spec R пучком $O\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{O\}\}\}$(сущность, которая собирает функции, определенные локально, т.е. подмножества). Эталон пространства и связки называется аффинной схемой. Учитывая аффинную схему, базовое кольцо R может быть восстановлено как глобальные разделы в $O\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{O\}\}\}$. Более того, это взаимно однозначное соответствие между кольцами и аффинными схемами также совместимо с гомоморфизмами колец: любое f: R → S порождает непрерывное отображение в противоположном направлении

Spec S → Spec R, q ↦ f (q), т.е. любой простой идеал S отображается в его прообраз под f, который является простым идеалом R.

Результирующая эквивалентность две упомянутые категории точно отражают алгебраические свойства колец геометрическим образом.

Подобно тому, что многообразия локально задаются открытыми подмножествами R, аффинные схемы являются локальными моделями для схем, которые являются объект изучения алгебраической геометрии. Таким образом, некоторые представления о коммутативных кольцах вытекают из геометрической интуиции.

Размерность

Размерность (или измерение) Крулля dim R кольца R измеряет «размер» кольца, грубо говоря, подсчитывая независимые элементы в R. Размерность алгебр над поле k может быть аксиоматизировано четырьмя свойствами:

• Размерность является локальным свойством: dim R = sup p ∊ Spec R dim R p.
• Размерность не зависит от нильпотентных элементов: если I ⊆ R нильпотентно, тогда dim R = dim R / I.
• Размерность остается постоянной при конечном расширении: если S - R-алгебра, конечно порожденная как R-модуль, то dim S = dim R.
• Размер калибруется dim k [X 1,..., X n ] = n. Эта аксиома мотивирована тем, что кольцо многочленов от n переменных рассматривается как алгебраический аналог n-мерного пространства.

Размерность определяется для любого кольца R как супремум длин n цепочек простых идеалов

p0⊊ p 1 ⊊... ⊊ p n.

Например, поле нульмерно, так как единственный простой идеал - это нулевой идеал. Целые числа являются одномерными, поскольку цепочки имеют вид (0) ⊊ (p), где p - простое число. Для нётеровых колец, а также нелокальных колец размерность может быть бесконечной, но нётеровы локальные кольца имеют конечную размерность. Среди четырех вышеупомянутых аксиом первые две являются элементарными следствиями определения, тогда как оставшиеся две основаны на важных фактах из коммутативной алгебры, восходящей теореме и Крулля. Теорема о главном идеале.

Гомоморфизм колец или, говоря проще, просто отображение - это отображение f: R → S такое, что

f (a + b) = f (a) + f (b), f (ab) = f (a) f (b) и f (1) = 1.

Эти условия гарантируют, что f (0) = 0. Как и для других алгебраических структур, гомоморфизм колец Таким образом, карта совместима со структурой рассматриваемых алгебраических объектов. В такой ситуации S также называется R-алгеброй, понимая, что s в S можно умножить на некоторое r из R, установив

r · s: = f (r) · s.

Ядро и образ f определяются как ker (f) = {r ∈ R, f (r) = 0} и im (f) = f (R) = {f (r), r ∈ R}. Ядро - это идеал кольца R, а изображение - подкольцо кольца S.

Гомоморфизм колец называется изоморфизмом, если он биективен. Примером изоморфизма колец, известного как китайская теорема об остатках, является

$Z\; /\; n\; =\; ⨁\; i\; =\; 0\; k\; Z\; /\; pi\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{Z\}\; /\; n\; =\; \backslash \; bigoplus\; \_\; \{i\; =\; 0\}\; ^\; \{k\}\; \backslash \; mathbf\; \{Z\}\; /\; p\_\; \{i\}\}$

где n = p 1p2... p k - произведение попарно различных простые числа.

Коммутативные кольца вместе с гомоморфизмами колец образуют категорию. Кольцо Z является исходным объектом в этой категории, что означает, что для любого коммутативного кольца R существует единственный кольцевой гомоморфизм Z → R. На этой карте целое число n можно рассматривать как элемент R. Например, биномиальная формула

$(a\; +\; b)\; n\; =\; \sum \; k\; =\; 0\; n\; (nk)\; akbn\; -\; k\; \{\backslash \; displaystyle\; (\; a\; +\; b)\; ^\; \{n\}\; =\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; ^\; \{n\}\; \{\backslash \; binom\; \{n\}\; \{k\}\}\; a\; ^\; \{k\}\; b\; ^\; \{nk\}\}$

который действителен для любого два элемента a и b в любом коммутативном кольце R понимаются в этом смысле, интерпретируя биномиальные коэффициенты как элементы R с использованием этого отображения.

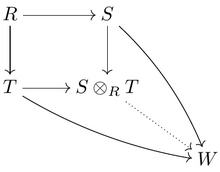Универсальное свойство для S ⊗ R T гласит, что для любых двух отображений S → W и T → W, которые коммутируют внешний четырехугольник, существует уникальное отображение S ⊗ R T → W, что заставляет всю диаграмму коммутировать.

Учитывая две R-алгебры S и T, их тензорное произведение

S ⊗ RT

снова является коммутативной R-алгеброй. В некоторых случаях тензорное произведение может служить для нахождения T-алгебры, которая относится к Z, как S относится к R. Например,

R [X] ⊗ R T = T [X].

Конечная генерация

R-алгебра S называется конечно порожденной (как алгебра), если существует конечное число элементов s 1,..., s n, так что любой элемент s выражается как многочлен от s i. Эквивалентно S изоморфна

R [T 1,..., T n ] / I.

Гораздо более сильным условием является то, что S равно конечно порожденный как R-модуль, что означает, что любое s может быть выражено как R-линейная комбинация некоторого конечного множества s 1,..., s n.

Кольцо называется локальным, если оно имеет только один максимальный идеал, обозначенный m. Для любого (не обязательно локального) кольца R локализация

Rp

в простом идеале p локальна. Эта локализация отражает геометрические свойства Spec R "около p". Некоторые понятия и проблемы коммутативной алгебры могут быть сведены к случаю, когда R локально, что делает локальные кольца особенно глубоко изученным классом колец. поле остатков R определяется как

k = R / m.

Любой R-модуль M дает k-векторное пространство, заданное M / mM. Лемма Накаямы показывает, что этот отрывок сохраняет важную информацию: конечно порожденный модуль M равен нулю тогда и только тогда, когда M / mM равно нулю.

Регулярные локальные кольца

кривая кубической плоскости (красная), определяемая уравнением y = x (x + 1), имеет сингулярность в начале координат, т. Е. кольцо k [x, y] / y - x (x + 1) не является правильным кольцом. Касательный конус (синий) представляет собой объединение двух прямых, что также отражает особенность.

k-векторное пространство m / m является алгебраическим воплощением котангенсного пространства. Неформально элементы m можно рассматривать как функции, которые обращаются в нуль в точке p, тогда как m содержит те, которые обращаются в нуль с порядком не ниже 2. Для любого нётерова локального кольца R выполняется неравенство

dim k m / m ≥ dim R

, что отражает идею о том, что кокасательное (или, что то же самое, касательное) пространство имеет, по крайней мере, размерность пространства Spec R. Если в этой оценке выполняется равенство, R называется обычное местное кольцо. Нётерово локальное кольцо является правильным тогда и только тогда, когда кольцо (которое является кольцом функций на касательном конусе )

$⨁\; nmn\; /\; mn\; +\; 1\; \{\backslash \; displaystyle\; \backslash \; bigoplus\; \_\; \{n\}\; m\; ^\; \{n\}\; /\; m\; ^\; \{n\; +\; 1\}\}$

изоморфно кольцу многочленов над k. Вообще говоря, регулярные локальные кольца чем-то похожи на кольца многочленов. Регулярные локальные кольца являются UFD.

Кольца дискретного нормирования оснащены с функцией, которая присваивает целое число любому элементу r. Это число, называемое оценкой r, можно неформально рассматривать как нулевой или полюсный порядок r. Дискретные оценочные кольца - это в точности одномерные регулярные локальные кольца. Например, кольцо ростков голоморфных функций на римановой поверхности является кольцом дискретного нормирования.

Полные пересечения

Скрученная кубика (зеленая) является множеством- теоретическое полное пересечение, но не полное пересечение.

Согласно теореме Крулля об основном идеале, основополагающем результате в теории размерности колец, размер

R = k [T 1,..., T r ] / (f 1,..., f n)

не меньше r - n. Кольцо R называется полным кольцом пересечений, если его можно представить способом, который достигает этой минимальной границы. Это понятие также в основном изучается для локальных колец. Любое регулярное локальное кольцо является полным кольцом пересечений, но не наоборот.

Кольцо R является теоретико-множественным полным пересечением, если редуцированное кольцо, ассоциированное с R, т. Е. Кольцо, полученное путем деления всех нильпотентных элементов, является полным пересечением. По состоянию на 2017 год вообще неизвестно, являются ли кривые в трехмерном пространстве теоретико-множественными полными пересечениями.

Кольца Коэна – Маколея

глубина локальное кольцо R - количество элементов в некоторой (или, как можно показать, любой) максимальной регулярной последовательности, т. е. последовательность a 1,..., a n ∈ m такое, что все a i являются ненулевыми делителями в

R / (a ​​1,..., a i-1).

Для любого локального Кольцо Нётерова, выполняется неравенство

depth (R) ≤ dim (R)

. Локальное кольцо, в котором имеет место равенство, называется кольцом Коэна – Маколея. Локальные полные кольца пересечений и a fortiori, правильные локальные кольца - это Коэна – Маколея, но не наоборот. Коэн – Маколей объединяет желаемые свойства регулярных колец (например, свойство быть универсально цепными кольцами, что означает, что (ко) размерность кольца простые числа хорошо себя ведут), но они также более устойчивы к факторизации, чем обычные локальные кольца.

Есть несколько способов построить новые кольца из уже имеющихся. Целью таких конструкций часто является улучшение определенных свойств кольца, чтобы сделать его более понятным. Например, область целостности, которая является целиком замкнутой в своем поле дробей, называется нормальным. Это желательное свойство, например, любое нормальное одномерное кольцо обязательно правильное. Отображение нормального кольца называется нормализацией.

Пополнения

Если I - идеал в коммутативном кольце R, степени I образуют топологические окрестности числа 0, что позволяет рассматривать R как топологическое кольцо. Эта топология называется I-адической топологией. Тогда R можно дополнить по этой топологии. Формально I-адическое пополнение - это обратный предел колец R / I. Например, если k - поле, k [[X]], кольцо формальных степенных рядов с одной переменной над k, является I-адическим пополнением k [X], где I - главный идеал порожденный X. Это кольцо служит алгебраическим аналогом диска. Аналогично, кольцо целых p-адических чисел является пополнением Z относительно главного идеала (p). Любое кольцо, изоморфное собственному пополнению, называется полным..

Полные локальные кольца удовлетворяют лемме Гензеля, которая, грубо говоря, позволяет распространить решения (различных задач) над полем вычетов k на R.

Некоторые более глубокие аспекты коммутативных колец были изучены с использованием методов из гомологической алгебры. Хохстер (2007) перечисляет некоторые открытые вопросы в этой области активных исследований.

Проективные модули и Ext-функторы

Проективные модули могут быть определены как прямые слагаемые свободных модулей. Если R является локальным, любой конечно порожденный проективный модуль фактически свободен, что дает содержание аналогии между проективными модулями и векторными расслоениями . Теорема Квиллена – Суслина утверждает, что любой конечно порожденный проективный модуль над k [T 1,..., T n ] (поле ka) свободен, но в целом эти два понятия различаются. Локальное нётерово кольцо является регулярным тогда и только тогда, когда его глобальная размерность конечна, скажем n, что означает, что любой конечно порожденный R-модуль имеет разрешение по проективным модулям длины не более п.

Доказательство этого и других связанных утверждений основывается на использовании гомологических методов, таких как Ext функтор. Этот функтор является производным функтором функтора

Hom R (M, -).

Последний функтор точен, если M проективен, но не иначе: для сюръективное отображение E → F R-модулей, отображение M → F может не продолжаться до отображения M → E. Высшие функторы Ext измеряют неточность Hom-функтора. Важность этой стандартной конструкции в основах гомологической алгебры можно увидеть из того факта, что локальное нетерово кольцо R с полем вычетов k является регулярным тогда и только тогда, когда

Ext (k, k)

обращается в нуль для всех достаточно больших n. Более того, размерности этих Ext-групп, известных как числа Бетти, полиномиально растут по n тогда и только тогда, когда R является локальным кольцом полного пересечения. Ключевым аргументом в таких соображениях является комплекс Кошуля, который обеспечивает явное свободное разрешение поля вычетов k локального кольца R в терминах регулярной последовательности.

Плоскостность

тензорное произведение - еще один неточный функтор, релевантный в контексте коммутативных колец: для общего R-модуля M функтор

M ⊗ R−

- это только верно. Если это точно, M называется плоский. Если R локально, любой конечно представленный плоский модуль не имеет конечного ранга, а значит, проективен. Несмотря на то, что плоскость определяется в терминах гомологической алгебры, она имеет глубокие геометрические последствия. Например, если R-алгебра S плоская, размеры слоев

S / pS = S ⊗ R R / p

(для простых идеалов p в R) имеют " ожидаемая размерность, а именно dim S - dim R + dim (R / p).

Согласно теореме Веддерберна, каждое конечное тело коммутативно и, следовательно, является конечным полем. Другое условие, обеспечивающее коммутативность кольца, согласно Джекобсону, заключается в следующем: для каждого элемента r кольца R существует целое число n>1 такое, что r = r. Если r = r для каждого r, кольцо называется булевым кольцом. Известны и более общие условия, гарантирующие коммутативность кольца.

Градиентно-коммутативные кольца

A пара штанов - это кобордизм между круг и два непересекающихся круга. Классы кобордизмов с декартовым произведением в качестве умножения и непересекающимся объединением в качестве суммы образуют кольцо кобордизмов.

A градуированное кольцо R = ⨁ i∊ZRiis называется градуированно-коммутативным, если

ab = (−1)

Если R i соединены дифференциалами ∂, так что абстрактная форма правила произведения , т. Е.

∂ (ab) = ∂ (a) b + (−1) ∂ (b),

R называется коммутативной дифференциальной градуированной алгеброй (cdga).. Примером может служить комплекс дифференциальных форм на многообразии, с умножением, данным внешним продуктом, является cdga. Когомологии cdga - это градуированно-коммутативное кольцо, иногда называемое кольцом когомологий . Таким образом, возникает широкий спектр примеров градуированных колец. Например, кольцо Лазара - это кольцо классов кобордизмов комплексных многообразий.

Градуированно-коммутативное кольцо относительно градуировки по Z / 2 (в отличие от Z ) называется супералгеброй.

родственной понятие является почти коммутативным кольцом, что означает, что R фильтруется таким образом, что связанное градуированное кольцо

gr R: = ⨁ F i R / ⨁ Fi−1R

is commutative. An example is the Weyl algebra and more general rings of differential operators.

Simplicial commutative rings

A simplicial commutative ring is a simplicial object in the category of commutative rings. They are building blocks for (connective) derived algebraic geometry. A closely related but more general notion is that of E∞-ring.

• Almost ring, a certain generalization of a commutative ring.
• Divisibility (ring theory) : nilpotent element, example: dual numbers
• Ideals and modules: Radical of an ideal, Morita equivalence
• Ring homomorphisms: integral element : Cayley–Hamilton theorem, Integrally closed domain, Krull ring, Krull–Akizuki theorem
• Primes: Prime avoidance lemma, Jacobson radical, Nilradical of a ring, Spectrum: Compact space, Connected ring, Differential calculus over commutative algebras, Banach–Stone theorem
• Local rings: Gorenstein ring : Duality (mathematics), Eben Matlis ; Dualizing module, Popescu's theorem, Artin approximation theorem.
• "Applications" (commutative rings arising in mathematics): Holomorphic functions, Algebraic K-theory, Topological K-theory, Divided power structures, Witt vectors, Hecke algebra, Fontaine's period rings, Cluster algebra, Convolution algebra (of a commutative group), see also Fréchet algebra

1. ^This notion can be related to the spectrum of a linear operator, see Spectrum of a C*-algebra and Gelfand representation.

Citations

1. ^Matsumura, §7, Remarks, p. 143) harvtxt error: no target: CITEREFMatsumura (help )
2. ^Matsumura, §19, Theorem 48) harvtxt error: no target: CITEREFMatsumura (help )
3. ^Lyubeznik (1989)
4. ^Eisenbud (1995, Corollary 18.10, Proposition 18.13)
5. ^See also Serre–Swan theorem.
6. ^Christensen, Striuli Veliche (2010)
7. ^Jacobson 1945
8. ^Pinter-Lucke 2007

• Atiyah, Michael ; Macdonald, I. G. (1969), Introduction to commutative algebra, Addison-Wesley Publishing Co.
• Balcerzyk, Stanisław; Józefiak, Tadeusz (1989), Commutative Noetherian and Krull rings, Ellis Horwood Series: Mathematics and its Applications, Chichester: Ellis Horwood Ltd., ISBN 978-0-13-155615-7
• Balcerzyk, Stanisław; Józefiak, Tadeusz (1989), Dimension, multiplicity and homological methods, Ellis Horwood Series: Mathematics and its Applications., Chichester: Ellis Horwood Ltd., ISBN 978-0-13-155623-2
• Christensen, Lars Winther; Striuli, Janet; Velic he, Oana (2010), "Growth in the minimal injective resolution of a local ring", Journal of the London Mathematical Society, Second Series, 81(1): 24–44, arXiv :0812.4672, doi :10.1112/jlms/jdp058
• Eisenbud, David (1995), Commutative algebra. With a view toward algebraic geometry., Graduate Texts in Mathematics, 150, Berlin, New York: Springer-Verlag, ISBN 978-0-387-94268-1, MR 1322960
• Hochster, Melvin (2007), "Homological conjectures, old and new" (PDF), Illinois J. Math., 51(1): 151–169, doi :10.1215/ijm/1258735330, archived from the original (PDF) on 2019-10-29, retrieved 2017-08-01
• Jacobson, Nathan (1945), "Structure theory of algebraic algebras of bounded degree", Annals of Mathematics, 46(4): 695–707, doi :10.2307/1969205, ISSN 0003-486X, JSTOR 1969205
• Kaplansky, Irving (1974), Commutative rings (Revised ed.), University of Chicago Press, MR 0345945
• Lyubeznik, Gennady (1989), "A survey of problems and results on the number of defining equations", Representations, resolutions and intertwining numbers, pp. 375–390, Zbl 0753.14001
• Matsu mura, Hideyuki (1989), Commutative Ring Theory, Cambridge Studies in Advanced Mathem atics (2nd ed.), Cambridge University Press, ISBN 978-0-521-36764-6
• Nagata, Masayoshi (1975) [1962], Local rings, Interscience Tracts in Pure and Applied Mathematics, 13, Interscience Publishers, pp. xiii+234, ISBN 978-0-88275-228-0, MR 0155856
• Pinter-Lucke, James (2007), "Commutativity conditions for rings: 1950–2005", Expositiones Mathematicae, 25(2): 165–174, doi :10.1016/j.exmath.2006.07.001, ISSN 0723-0869
• Zariski, Oscar ; Samuel, Pierre (1958–60), Commutative Algebra I, II, University series in Higher Mathematics, Princeton, N.J.: D. van Nostrand, Inc.(Reprinted 1975-76 by Springer as volumes 28-29 of Graduate Texts in Mathematics.)