В математике, двойственность перевод концепции, теоремы или математические структуры в другие концепции, теоремы или структуры, взаимно однозначно, часто (но не всегда) с помощью операции инволюции : если двойным является A B, то двойным к B A Такие инволюции иногда имеют неподвижные точки, так что двойным к A является сам A. Например, теорема Дезарга является самодуальной в этом смысле при стандартной двойственности в проективной геометрии.
В математическом контексте двойственность имеет множество значения. Он был описан как «очень распространенная и важная концепция в (современной) математике» и «важная общая тема, которая проявляется почти во всех областях математики».
Многие математические двойственности между объектами двух типов соответствуют в пары, билинейных функций от объекта одного типа и другого объекта второго типа к некоторому семейству скаляров. Например, двойственность линейной алгебры таким билинейным отображением пар векторных пространств в скаляры, двойственность между распределениями и соответствует тестовыми функциями соответствует объединению, в котором интегрируется распределение по тестовой функции, и двойственность Пуанкаре аналогично рассматриваемого пересечения, рассматриваемому как пара между подмногообразиями данного разнообразия.
Из С точки теории зрения категорий, двойственность также может рассматриваться как функтор, по крайней мере, в сфере векторных пространств. Этот функтор назначает каждому пространству его двойное пространство, конструкция pullback назначает каждую стрелку f: V → W ее двойное f: W → V.
По словам Майкла Атьи,
Двойственность в математике - это не теорема, а «принцип».
Следующий список примеров показывает общие черты многих дуальностей, но также указывает, что точное значение двойственности может отличаться от случая случаю.
Простая, возможно, самая простая двойственность возникает из рассмотрения подмножеств фиксированного набора S. Для любого подмножества A⊆ Sдополнение Aсостоит из всех тех элементов в S, которые не содержатся в A. Это снова подмножество S. Взятие дополнения имеет следующие свойства:
Эта двойственность проявлялась в топологии как двойственность открытые и закрытые подмножества некоторого фиксированного топологического пространства X: подмножество Uиз Xзакрыто и тогда только тогда, когда его дополнение в Xоткрыто. По этой причине многие теоремы о замкнутых множествах двойственны теоремам об открытых множествах. Например, любое объединение открытого множеств открыто, поэтому любое пересечение замкнутых множеств замкнуто. внутренний набора - это самый большой открытый набор, предостався в нем, а закрытие - это наименьший закрытый набор, который его содержит. Из-за двойственности дополнение внутренней части любого набора Uравно замыкание дополнения U.
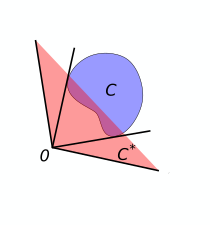 Набор C(синий) и его двойной конус C(красный).
Набор C(синий) и его двойной конус C(красный). Двойственность в геометрии обеспечивается конструкцией двойного конуса. Дан набор 





для всех точек 





 ,
,  содержится в
содержится в  . (Для некоторых
. (Для некоторых  , а именно конусов, два фактически равны.)
, а именно конусов, два фактически равны.)Два других свойства переносятся без изменений:
 превращается во включение в противоположном направлении (
превращается во включение в противоположном направлении ( ).
). и
и  плоскости,
плоскости,  содержится в
содержится в  тогда и только, когда
тогда и только, когда  содержится в
содержится в  .
.Очень важный пример двойственности в линейной алгебре связав с любым векторным пространством Vего двойное векторное пространство V. Элементы являются k-линейные карты 

Особенности этой двойственности Это то, что Vи Vизоморфны для определенных объектов, именно для конкретных векторных пространств. Это находится в некотором смысле удачное совпадение, для достижения такого изоморфизма требуется некоторый выбор, например выбор базиса из V. Это также верно в случае, если Vявляется гильбертовым пространством, согласно теореме о представлении Рисса.
Во всех дуальностях, обсуждавшихся ранее, двойственность объекта имеет тот же вид как сам объект. ранство снова является векторным пространством. Многие утверждения дуальности не относятся к этому типу.. Напротив, такие двойственности обнаруживают тесную связь между объектами, кажется бы, разной природы. Один из примеров такой более общей двойственности взят из теории Галуа. Для фиксированного расширения Галуа K/ Fможно связать группу Галуа Gal (K/E) с любым промежуточным полем E(т. Е. F⊆ E⊆ K). Эта группа является подгруппой группы Галуа G= Gal (K/F). И наоборот, для любой такой подгруппы H⊆ Gсуществует фиксированное поле K, состоящее из элементов, определенных элементов в H.
По сравнению с вышеупомянутым, эта двойственность имеет следующие особенности:
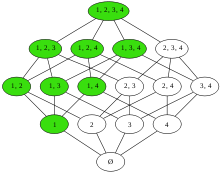 диаграммы Хассе множество степеней {1, 2, 3, 4}, частично упорядоченное ⊂., т. е. упорядочение по, получается перевертыванием диаграмм. Зеленые узлы образуют верхнее множество и нижний набор в исходном и двойном порядке, соответственно.
диаграммы Хассе множество степеней {1, 2, 3, 4}, частично упорядоченное ⊂., т. е. упорядочение по, получается перевертыванием диаграмм. Зеленые узлы образуют верхнее множество и нижний набор в исходном и двойном порядке, соответственно. Учитывая poset P= (X, ≤) (сокращение от частично упорядоченного набора; т. Е. Набор, который имеет понятие упорядочивания, но в котором два элемента н е обязательно могут быть размещены по порядку относительно каждого из нее), дуальный poset P= (X, ≥) содержит тот же основной набор, но обратное отношение. Знакомые примеры двойных частичных порядков включают
. Понятие, определенное для частичного порядка P, будет соответствовать двойному понятию на двойном чугу. P. Например, минимальный элемент из Pбудет максимальным элементом из P: минимальность и максимальность являются двойственными понятиями в теории порядка. Другие пары двойственных понятий: верхняя и нижняя границы, нижние наборы и верхние наборы и идеалы и фильтры.
В топологии открытые числа и закрытые числа являются двойственными понятиями: дополнение большого числа замкнуто, и наоборот. В теории матроида семейство множеств, совместных независимых множеств данного матроида, сами по себе разные матроиды, называемый двойным матроидом.
 Особенности куба и его двойной октаэдр соответствуют одному к одному с перевернутыми размерами.
Особенности куба и его двойной октаэдр соответствуют одному к одному с перевернутыми размерами. Есть много различных, но взаимосвязанных двойных объектов, в которых геометрические или топологические объекты соответствуют другим объектам того же типа, но с изменением размеров характеристик объектов. Классическим примером этого является двойственность платоновых тел, в которой куб и октаэдр образуют дуальную пару, додекаэдр и икосаэдр образуют дуальную пару, а тетраэдр самодвойственен. Двойственный многогранник любой из этих многогранников может быть образован как выпуклая оболочка центральных точек каждой грани прямого многогранника, так что вершины двойные соответствуют одному к одному с гранями первичного. Точно так же каждое ребро дуального соответствует вершине простого, каждая грань дуального соответствует вершине простого. Эти соответствующие сохраняют инцидентность: если две части первичного многогранника касаются друг друга, то же самое происходит и с двумя частями двойного многогранника . В более общем смысле, используя концепцию полярного взаимного движения, любой выпуклый многогранник или, в более общем смысле, любой выпуклый многогранник, соответствует двойному многограннику или двойной многогранник с i-мерным признаком n-мерного многогранника, соответствующего (n− i- 1) -мерному объекту двойственного многогранника. Сохраняющая инцидентность природа двойственности отражается в том факте, что решетки граней прямых и двойных многогранников или многогранников сами по себе являются теоретико-порядков двойниками. Двойственность многогранников и теоретико-упорядоченная двойственность - это инверсия : двойственность многогранника двойного многогранника любого многогранника является исходным многогранником, и, дважды обращенная все порядок, возвращается к исходному порядку. Выбор другого центра полярности приводит к геометрически различным двойным многогранникам, но все они имеют одинаковую комбинаторную структуру.
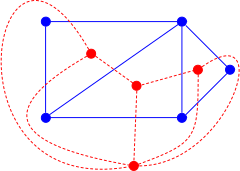 A плоский граф синим цветом, а его дуальный граф красным.
A плоский граф синим цветом, а его дуальный граф красным. Из любого трехмерного многогранника можно сформировать плоский граф, график его вершины и ребра. Двойственный многогранник имеет дуальный граф, граф с одной вершиной на каждой грань многогранника и с одним ребром на каждые две смежные грани. Та же концепция двойственности плоских графов может быть обобщена на графы, которые нарисованы на плоскости, но не выполнены из трехмерного многогранника, или, в более общем смысле, на в области более высокого вида: можно нарисуйте двойственные графы на поверхностях более высокого вида: граф, поместив по одной вершине в каждую область, ограниченную циклом ребер при встраивании, и нарисовав ребро, соединяющее любые две области, которые имеют общую границу. Важным примером этого типа является вычислительная геометрия : двойственность для любого конечного набора Sточек на плоскости между триангуляцией Делоне из Sи диаграмма Вороного из S. Как и в случае двойственных многогранников и двойственных многогранников, двойственность графов на поверхностях - это инволюция, обращающая размер: каждая вершина в прямом вложенном графе соответствует области двойного вложения, каждая в прямом пересечении ребро в прямом двойном, и каждая область прямого соответствует вершине дуального. Двойственный граф зависит от того, как вложен прямой граф: разные плоские вложения одного графа могут привести к разным двойным графам. Двойственность матроидов - это алгебраическое расширение двойственности плоского графа в том смысле, что двойной матроидовский матроида плоского графа изоморфен двойного графического матроидуственного графа.
В теории оптимизации также присутствует своего рода геометрическая двойственность, но не та, которая меняет размеры на противоположную. линейная программа может быть определена системой вещественных чисел (координаты точки в евклидовом пространстве 
В логике функции или отношения Aи Bсчитаются двойственными, если A(¬x) = ¬ B(x), где ¬ - логическое отрицание. Основная двойственность этого типа - двойственность кванторов и ∀ в классической логике. Они двойственны, потому что ∃ x.¬P(x) и ¬∀ x.P(x) эквивалентны для всех предикатов Pв классической логике: если существует x, для которого Pне выполнено, то неверно, что Pвыполнено для всех x(но обратное не имеет конструктивного значения). Из этой фундаментальной логической двойственности вытекают:
Другие аналогичные двойственности вытекают из эти:
Группа двойственностей может быть описана путем наложения для любого математического объекта Xнабора морфизмов Hom (X, D) в некоторый фиксированный объект D, со структурой, аналогичной структуре X. Иногда это называется внутренним Hom. В общем, это дает истинную двойственность только для конкретных вариантов D, и вВ этом случае X= Hom (X, D) упоминается как двойное для X. Всегда существует отображение из Xв двузначное, то есть двойное двойное двойственное,

Он присваивает некоторому x∈ Xкарту, которая ассоциируется с любой картой f: X→ D(т. Элементом в Hom (X, D)), значение f(x). В зависимости от рассматриваемой двойственности, а также от объекта Xэта карта может быть или не быть изоморфизмом.
Построение двойного пространства

, упомянутый во введении, является примером такой двойственности. В самом деле, набор морфизмов, т.е. линейных отображений, сам по себе образует векторное пространство. Упомянутая выше карта V→ Vвсегда инъективна. Он сюръективен и, следовательно, изоморфизм, если и только если размерность для Vконечна. Этот факт обеспечивает обслуживерные пространства без ссылок на базис.
Векторное пространство V изоморфно V в точности, если V конечерно. В этом случае такой изоморфизм эквивалентен невырожденной билинейной формы

В этом случае V называется внутренним пространством продукта. Например, если K является полем действительных или комплексных чисел, любая положительно определенная билинейная форма порождает такой изоморфизм. В римановой геометрии В исследовании как касательное пространство к многообразию, и такие положительные билинейные формы называются римановыми метриками. Их цель - измерение углов иний расстояний. Таким образом, двойственность является фундаментальной причиной этой области геометрии. Другое применение внутреннего алгебры продукта - это звезда Ходжа, которая обеспечивает соответствие между элементами внешней алгебры. Для n-мерного пространства звездный операторжа отображает k-формы в (n - k) -формы. Это может быть использовано для формулирования Максвелла. В этом облике двойственность, присущая внутреннему пространству продукта, меняет роль магнитного и электрического поля.
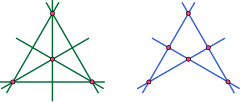 полный четырехугольник, конфигурация четырех точек и шести прямой на проективной плоскости (слева) и ее двойная конфигурация, полный четырехугольник, с четырьмя прямыми и шестью точками (справа).
полный четырехугольник, конфигурация четырех точек и шести прямой на проективной плоскости (слева) и ее двойная конфигурация, полный четырехугольник, с четырьмя прямыми и шестью точками (справа). В некоторых проективных плоскостях это возможно найти геометрические преобразования, которые отображают каждую точку проективной плоскости в линии, а каждую линию проективной плоскости в точку, с сохранением инцидентности. Для таких плоскостей возникает общий принцип двойственности в проективных плоскостях : для любых теоремы в такой плоской проективной геометрии замена терминов «точка» и «линия» везде приводит к новой, равнозначной теореме. Простым примером является то, что утверждение «две точки определяют уникальную линию, проходящую через эти точки» имеет двойное утверждение, что «две линии определяют уникальную точку, точку пересечения этих двух линий». Дополнительные примеры см. В разделе Двойные теоремы.
Концептуальное объяснение этого явления в некоторых плоскостях. Фактически, точки на проективной плоскости 







(Положительно определенная) билинейная форма

дает идентификацию этой проективной плоскости с 


В области топологических векторных пространств существует новая конструкция, заменяющая двойное пространство топологическое двойное векторное пространство. Существует несколько понятий топологического двойного пространства, и каждое из них порождает определенное понятие двойственности. Топологическое векторное пространство 


Примеры:

 ,
,  ,
,  - являются рефлексивными локально выпуклыми пространствами.
- являются рефлексивными локально выпуклыми пространствами.Двойственная решетка решетки Lзадается как

, который используется при построении торических разнообразий. Понтрягин, двойной к локально компактной топологической группе G, задается как

непрерывные групповые гомоморфизмы со значениями в круге (с умножением комплексных чисел как групповой операцией).
В другой группе дуальностей одной теории переводятся объекты другой теории и карты между объектами в первая теория переводится в морфизмы во второй теории, но с обратным направлением. Используя язык теории категорий, это составляет контравариантный функтор между двумя категориями Cи D:
F: C→ D, который для любых двух объектов X и Y из C дает карту
Хом C(X, Y) → Хом D(F(Y), F(X))Этот функтор может быть, а может и не быть эквивалентом стандартов. Существуют различные ситуации, когда такой функтор является эквивалентом между противоположной категорией Cиз Cи D. Используя двойственность этого типа, утверждение в первой теории может быть переведено в «двойное» утверждение во второй теории, где направление всех стрелок должно быть изменено на противоположное. Следовательно, любая двойственность между категориями Cи Dформально такая же, как эквивалентность между Cи D(Cи D). Что делает двойственность противоположной категории.
Категория, эквивалентная своей двойственной, называется самодуальной. Примером самодвойственной категории является категория гильбертовых пространств.
. Многие теоретико-категориальные понятия входят в понятие попарно в том смысле, что они соответствуют друг другу при рассмотрении противоположной категории. Например, декартовы произведения Y1× Y2и непересекающиеся объединения Y1⊔ Y2множеств двойственны друг другу в том смысле, что
Hom (X, Y1× Y2) = Hom (X, Y1) × Hom ( X, Y2)и
Hom (Y1⊔ Y2, X) = Hom (Y1, X) × Hom (Y2, X)для любого набора X. Это частный случай более общего явления двойственности, при котором пределы в категории Cсоответствуют копределам в противоположной категории C; другие примеры этого - это эпиморфизмы по сравнению с мономорфизмом, в частности факторные модули (или группы и т. д.) по сравнению с подмодулями, прямыми продуктами по сравнению с прямыми суммами (также называемыми копродукциями, чтобы подчеркнуть особенности). Следовательно, в некоторых случаях доказательства утверждений утверждений могут быть двойены сокращены вдвое, используя такое явление двойственности. ity, - это проективные и инъективные модули в гомологической алгебре, расслоения и кофибрации в топологии и более в общем плане категории моделей.
Два функтора F: C→ Dи G: D→ Cявляются сопряженными, если для всех объектов c в C и d в D
Hom D(F (c), d) ≅ Hom C(c, G(d)),естественным образом. Собственно, соответствие пределов и копределов является примером сопряжения, поскольку существует присоединение
colim: C↔ C: Δмежду функтором копредела, который присваивается любой диаграмме в Cпроиндексирован некоторой категорией Iего копредел и диагональный функтор, который отображает любой объект cиз Cна диаграмму констант, которая имеет cво всех местах. Соответственно,
Δ: C↔ C: lim.двойственность Гельфанда - это двойственность между коммутативными C * -алгебрами A и compact space Хаусдорфа X то же самое: оно присваивает X пространство непрерывных функций (которые обращаются в нуль на бесконечности) от X до C, комплексных чисел. И наоборот, пространство X может быть восстановлено из A как спектр оператора A. Двойственность Гельфанда и Понтрягина может быть выведена в степени формальным теоретико-категориальным способом.
Аналогичным образом. в алгебраической геометрии существует двойственность между коммутативными кольцами и аффинными схемами : каждому коммутативному кольцу A соответствует аффинный спектр, Spec A. И наоборот, если дана аффинная схема S, можно получить кольцо, взяв глобальные секции структурного пучка OS. гомоморфизмы колец находятся во взаимно однозначном соответствии с морфизмами аффинных, поэтому существует эквивалентность
Аффинные схемы являются локальными строительными блоками схем . Таким образом, предыдущий результат говорит о том, что локальная теория схем аналогична коммутативной алгебре, изучению коммутативных колец.
Некоммутативная геометрия черпает вдохновение из двойственности Гельфанда и изучает некоммутативные C * -алгебры, как если бы они были функциями в некотором воображаемом пространстве. Двойственность Таннаки – Крейна является некоммутативным аналогом двойственности Понтрягина.
В ряде ситуаций две категории, двойственные друг другу, являются фактически возникает из частично упорядоченных множеств, т. е. существует определенное понятие объекта «меньше» другого. Двойственность, которая уважает рассматриваемые порядки, известна как связь Галуа. Примером может служить стандартная двойственность в теории Галуа, упомянутая во введении: большее расширение поля соответствует - при отображении, которое сопоставляет любому расширению L ⊃ K (внутри некоторого фиксированного большего поля Ω) группу Галуа Gal ( Ω / L) - меньшей группе.
Совокупность всех открытых подмножеств топологического пространства X образует полную алгебру Гейтинга. Существует двойственность, известная как двойственность камня, соединяющая трезвые пространства и пространственные локации.
двойственность Понтрягина дает двойственность в категории локально компактных абелевых групп : для любой такой группы G, группа характеров
, заданная непрерывными групповыми гомоморфизмами из G в круговую группу S, может быть наделена компактно-открытой топология. Двойственность Понтрягина утверждает, что группа характеров снова является локально компактной абелевой и что
Более того, дискретные группы соответствуют компактным абелевым группам ; конечные группы соответствуют конечным группам. С одной стороны, Понтрягин - частный случай двойственности Гельфанда. С другой стороны, это концептуальная причина анализа Фурье, см. Ниже.
В анализа проблемы часто решаются путем перехода к двойному описанию функций и операторов.
Преобразование Фурье переключает функции в векторном и его двойным:

и наоборот

Если f является L-функцией на R или R, скажем, то же и 

Теоремы, показывающие, что некоторые представляющие интерес объекты являются двойными пространствами (в смысле линейной алгебры) других интересующих объектов, часто называемых дуальностями. Многие из этих двойственностей задаются билинейным спариванием двух K-векторных пространств
Для идеальных пар, следовательно, изоморфизм A к двойным к B.
Двойственность Пуанкаре гладкого компактного комплексного разнообразия X заданные спариванием сингулярных когомологий с C -коцентентами (эквивалентно, когомологии пучка константного пучка C)
где n - (комплексная) размерность X. Двойственность Пуанкаре также может быть выражена как отношение сингулярных гомологий и когомологий де Рама, утверждено, что отображение

(интегрирование дифференциальной k-по 2n - k- (действующее) - размерный цикл) является идеальным спариванием.
Двойственность Пуанкаре также меняет размерность на противоположную; соответствует тому факту, что если топологическое плоский представлен как клеточный комплекс, то двойственное к комплексу (многомерное обобщение двойного графа) представляет то же самое многообразие. В двойственности Пуанкаре этот гомеоморфизм отражается в изоморфизме k-й группы гомологий и (n - k) й группа когомологий.
Тот же образец двойственности имеет место для гладкого проективного многообразия над сепарабельно замкнутым полем, используя l-адические когомологии с Qℓ-коенты вместо этого. Далее это обобщается на возможно сингулярные многообразия, используя вместо этого когомологию пересечений, двойственность, называемую двойственностью Вердье. двойственностью Серра или когерентная двойственность другим применением выше, но вместо этого применяемого к когомологиим когерентных пучков.
Современная формулировка этих двойственностей может быть сделана с использованием производных категорий и некоторых функторов прямого и обратного изображения пучков (относительно когерентных пучков для когерентной двойственности). и обратного изображения пучков (относительно классической аналитической топологии многообразия двойственности Пуанкаре, l-адических пучков и этальной топологии ).
Еще одна группа подобных примеров двойного образования в арифметике : этальные когомологии конечных, локальных и глобальных полей (также известные как когомологии Галуа, поскольку этальные когомологии над полем эквивалентны групповым когомологиям (абсолютной) группы Галуа поля) допускают аналогичные пары. Абсолютная группа Галуа G (Fq) конечного поля, например, изоморфна 
является прямым следствием двойственности Понтрягина конечных групп. Для локальных и глобальных полей существуют аналогичные утверждения (локальная двойственность и глобальная или двойственность Пуату - Тейта ).