Войти
Выбор кубических кривых. Щелкните изображение, чтобы просмотреть подробную информацию на странице информации. В математике, кривая кубической плоскости - это плоская алгебраическая кривая C, определяемая кубическим уравнением
применяется к однородным координатам x: y: z для проективной плоскости ; или неоднородная версия для аффинного пространства, определяемая установкой z = 1 в таком уравнении. Здесь F - ненулевая линейная комбинация мономов третьей степени
Их десять; следовательно, кубические кривые образуют проективное пространство размерности 9 над любым заданным полем K. Каждая точка P налагает одно линейное условие на F, если мы попросим, чтобы C проходил через P. Следовательно, мы можем найти некоторую кубическую кривую через любые девять заданных точек, которые могут быть вырожденными и могут не быть уникальными, но будут уникальными и невырожденным, если точки находятся в общем положении ; сравните с двумя точками, определяющими линию, и как пять точек определяют конус. Если две кубики проходят через данный набор из девяти точек, то на самом деле пучок кубиков проходит, и точки удовлетворяют дополнительным свойствам; см. Теорема Кэли – Бахараха.
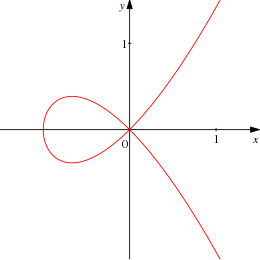Особая кубика y = x ⋅ (x + 1). Параметризация задается формулой t ↦ (t - 1, t (t - 1)). Кубическая кривая может иметь особую точку, и в этом случае она имеет параметризацию через проективную линию. В противном случае известно, что неособая кубическая кривая имеет девять точек перегиба над алгебраически замкнутым полем, таким как комплексные числа. Это можно показать, взяв однородную версию матрицы Гессе, которая снова определяет кубику, и пересекая ее с C; пересечения затем подсчитываются по теореме Безу. Однако только три из этих точек могут быть реальными, так что остальные нельзя увидеть в реальной проективной плоскости, нарисовав кривую. Девять точек перегиба неособой кубики обладают тем свойством, что каждая прямая, проходящая через две из них, содержит ровно три точки перегиба.
Реальные точки кубических кривых изучал Исаак Ньютон. Вещественные точки неособой проективной кубики распадаются на один или два «овала». Один из этих овалов пересекает каждую действительную проективную прямую и, таким образом, никогда не ограничивается, когда кубика проводится в евклидовой плоскости ; он выглядит как одна или три бесконечных ветви, содержащие три реальные точки перегиба. Другой овал, если он существует, не содержит реальной точки перегиба и выглядит либо как овал, либо как две бесконечные ветви. Как и для конических участков, линия разрезает этот овал максимум в двух точках.
Неособая плоская кубика определяет эллиптическую кривую над любым полем K, для которого определена точка. Эллиптические кривые в настоящее время обычно изучаются в виде некоторого варианта эллиптических функций Вейерштрасса, определяющих квадратичное расширение поля рациональных функций, полученное путем извлечения квадратного корня из кубический. Это действительно зависит от наличия рациональной точки K- , которая служит точкой на бесконечности в форме Вейерштрасса. Есть много кубических кривых, у которых нет такой точки, например, когда K - поле рационального числа.
Особые точки неприводимой плоской кубической кривой весьма ограничены: одна двойная точка или одна куспид. Приводимая плоская кубическая кривая представляет собой либо конику и линию, либо три прямые, и, соответственно, имеет две двойные точки или тактовый узел (если коника и линия), или до трех двойных точек или одну тройную точка (параллельные строки ), если три строки.
Предположим, что ABC - треугольник со сторонами a = | BC |, b = | CA |, c = | AB |. По сравнению с ABC, многие именованные кубики проходят через хорошо известные точки. В приведенных ниже примерах используются два вида однородных координат: трилинейные и барицентрические.
. Чтобы преобразовать трилинейные в барицентрические в кубическом уравнении, замените следующим образом:
для преобразования из барицентрической системы в трилинейную используйте
Многие уравнения для кубиков имеют вид
В приведенных ниже примерах такие уравнения записываются более кратко в "обозначении циклической суммы", например:
Кубики, перечисленные ниже, могут быть определены в члены изогонально сопряженного, обозначенного X *, точки X не на боковой линии ABC. Далее следует конструкция X *. Пусть L A будет отражением линии XA относительно биссектрисы внутреннего угла угла A, и аналогично определим L B и L C. Тогда три отраженные линии совпадают в X *. В трилинейных координатах, если X = x: y: z, то X * = 1 / x: 1 / y: 1 / z.
Трилинейное уравнение: [циклическая сумма (cos A - 2 cos B cos C) x (y - z)] = 0
Барицентрическое уравнение: [циклическое sum (a (b + c) + (b - c) - 2a) x (cy - bz)] = 0
Кубика Нойберга (названная в честь Джозефа Жан-Батиста Нойберга ) геометрическое место точки X такой, что X * находится на прямой EX, где E - точка бесконечности Эйлера (X (30) в Энциклопедии центров треугольников ). Кроме того, эта кубика является геометрическим местом X, так что треугольник X AXBXCперспективен для ABC, где X AXBXC- отражение X в прямых BC, CA, AB соответственно
Нойберга кубический проходит через следующие точки: центр окружности, центр окружности, ортоцентр, обе точки Ферма, обе изодинамические точки, точка бесконечности Эйлера, центры других треугольников, эксцентрики, отражения A, B, C на сторонах ABC и вершины шести равносторонних треугольников, воздвигнутых по сторонам ABC.
Для графического представления и обширного списка свойств кубики Нойберга см. K001 в книге Берхарда Гиберта Кубики в плоскости треугольника.
Пример кубики Томсона (черная кривая). X находится на кубике, так что изогональное сопряжение X (X ′) находится на прямой X (2) - X. Трилинейное уравнение: [циклическая сумма bcx (y - z)] = 0
Барицентрическое уравнение: [циклическая сумма x (cy - bz)] = 0
Кубика Томсона - это геометрическое место точки X такой, что X * находится на прямой GX, где G - центроид.
Кубика Томсона проходит через следующие точки: центр окружности, центр тяжести, центр описанной окружности, ортоцентр, симедианная точка, другие центры треугольников, вершины A, B, C, эксцентрики, середины сторон BC, CA, AB, и середины высот ABC. Для каждой точки P на кубике, но не на боковой линии кубики, изогональное сопряжение P также находится на кубике.
Графики и свойства см. В K002 в Кубики в плоскости треугольника.
Трилинейное уравнение: [циклическая сумма (cos A - cos B cos C) x (y - z)] = 0
Барицентрическое уравнение: [циклическая сумма (2a (b + c) + (b - c) - 3a) x (cy - bz) ] = 0
Кубика Дарбу - это геометрическое место точки X такой, что X * находится на прямой LX, где L - точка де Лоншана. Кроме того, эта кубика является геометрическим местом X, таким что педальный треугольник X является чевианом некоторой точки (лежащей на кубике Люка). Кроме того, эта кубика является геометрическим местом точки X такой, что педальный треугольник X и антицевианский треугольник X являются перспективными; перспектива лежит на кубике Томсона.
Кубика Дарбу проходит через центр окружности, центр описанной окружности, ортоцентр, точку де Лоншама, другие центры треугольников, вершины A, B, C, эксцентрики и противоположности A, B, C на описанной окружности. Для каждой точки P на кубике, но не на боковой линии кубики, изогональное сопряжение P также находится на кубике.
Для графики и свойств см. K004 в Кубики в плоскости треугольника.
Трилинейное уравнение: [циклическая сумма cos (B - C) x (y - z)] = 0
Барицентрическое уравнение: [циклическая сумма (a (b + c) - (b - c)) x (cy - bz)] = 0
Кубика Наполеона-Фейербаха - это геометрическое место точки X * на прямой NX, где N - центр из девяти точек (N = X (5) в Энциклопедии центров треугольников ).
Кубика Наполеона-Фейербаха проходит через центр окружности, центр окружности, ортоцентр, 1-ю и 2-ю точки Наполеона, другие центры треугольников, вершины A, B, C, эксцентрики, проекции центра тяжести на высоты, и центры шести равносторонних треугольников, воздвигнутых по сторонам ABC.
Для графики и свойств см. K005 в Кубики в плоскости треугольника.
Трилинейное уравнение: [циклическая сумма ( cos A) x (by - cz)] = 0
Барицентрическое уравнение: [циклическая сумма (b + c - a) x (y - z)] = 0
Кубика Люка есть геометрическое место точки X, такое что чевиан треугольник X является педальным треугольником некоторой точки; точка лежит на кубике Дарбу.
Кубика Лукаса проходит через центр тяжести, ортоцентр, точку Жергонна, точку Нагеля, точку де Лоншама, другие центры треугольников, вершины антикомплементарного треугольника и фокусы кругового эллипса Штейнера.
Графические изображения и свойства см. В K007 в Кубики в плоскости треугольника.
Трилинейное уравнение: [циклическая сумма bc (a - bc) x (y + z] = 0
Барицентрическое уравнение: [циклическая сумма (a - bc) x (cy + bz] = 0
Пусть A′B′C ′ - первый треугольник Брокара. Для произвольной точки X пусть X A, X B, X C - точки пересечения прямых XA ′, XB ′, XC ′ со сторонами BC, CA, AB, соответственно. 1-я кубика Брокара - это геометрическое место X, для которого точки X A, X B, X C коллинеарны.
1-й кубик Брокара проходит через центр тяжести, симедианную точку, точку Штейнера, центры других треугольников и вершины 1-го и 3-го треугольников Брокара.
Для графики. и свойства, см. K017 в Кубики в плоскости треугольника.
Трилинейное уравнение: [циклическая сумма bc (b - c) x (y + z] = 0
Барицентрическое уравнение: [циклическая сумма (b - c) x (cy + bz] = 0
Вторая кубика Брокара - геометрическое место точки X, для которой полюс прямой XX * в описанной конике, проходящей через X и X *, лежит на линии центра описанной окружности и симедианной точки (т. Е. Оси Брокара).
Вторая кубика Брокара проходит через центр тяжести, симедианную точку, обе точки Ферма, обе изодинамические точки, точку Парри, центры других треугольников и вершины 2-го и 4-го треугольников Брокара.
Для графики и свойств см. K018 в Кубики в плоскости треугольника.
Трилинейное уравнение: [циклическое sum a (b - c) x (y - z] = 0
Барицентрическое уравнение: [циклическая сумма a (b - c) x (cy - bz] = 0
Первое равное Кубика площадей - это геометрическое место точки X, такое что площадь чевианского треугольника X равна площади чевианского треугольника X *. Кроме того, эта кубика является геометрическим местом точки X, для которой X * находится на прямой S * X, где S - точка Штейнера. (S = X (99) в Энциклопедии центров треугольников ).
Первый равновеликий кубик проходит через центр, точку Штейнера и другие центры треугольников., 1-я и 2-я точки Брокара и эксцентрики.
Для графики и свойств см. K021 в Кубики в плоскости треугольника.
Трехлинейное уравнение: (bz + cx) (cx + ay) (ay + bz) = (bx + cy) (cy + ax) (az + bx)
Барицентрическое уравнение: [циклическая сумма a (a - bc) x (cy - bz)] = 0
Для любой точки X = x: y: z (трилинейной) пусть X Y = y: z: x и X Z = z: x: y. Вторая равная кубическая площадь - это геометрическое место X, такое, что площадь чевианового треугольника X Y равна площади чевианского треугольника X Z.
Второй равновеликий кубик проходит через центр, центр тяжести, симедианная точка и точки в Энциклопедии центров треугольников, индексированные как X (31), X (105), X (238), X (292), X (365), X (672), X (1453), X (1931), X (2053) и другие.
Для получения графических изображений и свойств см. K155 в Кубики в плоскости треугольника.
