Дифференцируемая функция

редактировать

Математическая функция, производная которой существует

В исчислении (ветвь математики ), дифференцируемая функция одной действительной переменной - это функция, производная которой существует в каждой точке в ее области. Другими словами, график дифференцируемой функции имеет не вертикальную касательную в каждой внутренней точке области определения. Дифференцируемая функция является гладкой (функция локально хорошо аппроксимируется как линейная функция в каждой внутренней точке) и не содержит излома, угла или выступа.

В более общем смысле, для x 0 как внутренней точки в области определения функции f, тогда f называется дифференцируемой в x 0 тогда и только тогда, когда производная f '(x 0) существует. Другими словами, график f имеет не вертикальную касательную в точке (x 0, f (x 0)). Функция f также называется локально линейной в x 0, поскольку она хорошо аппроксимируется линейной функцией вблизи этой точки.

Содержание

1 Дифференцируемость реальных функций одной переменной
2 Дифференцируемость и непрерывность
3 Классы дифференцируемости
4 Дифференцируемость в высших измерениях
5 Дифференцируемость в комплексном анализе
6 Дифференцируемые функции на многообразиях
7 См. также
8 Ссылки

Дифференцируемость вещественных функций одной переменной

Функция $f: U ⊂ R → R {\ displaystyle f: U \ subset \ mathbb {R} \ to \ mathbb {R}}$ ${\ displaystyle f: U \ subset \ mathbb {R} \ to \ mat hbb {R}}$ , определенный на открытом наборе $U {\ displaystyle U}$ $U$ , называется дифференцируемым в $a ∈ U {\ displaystyle a \ in U}$ ${\ displaystyle a \ in U}$ , если выполняется любое из следующих эквивалентных условий:

Производная $f '(a) = lim h → 0 f (a + h) - е (а) час {\ displaystyle f '(a) = \ lim _ {h \ to 0} {\ frac {f (a + h) -f (a)} {h}}}$ $f'(a)=\lim _{h\to 0}{\frac {f(a+h)-f(a)}{h}}$ существует.
Существует действительное число $L {\ displaystyle L}$ $L$ такое, что $lim h → 0 f (a + h) - f (a) - L чч знак равно 0 {\ displaystyle \ lim _ {h \ to 0} {\ frac {f (a + h) -f (a) -Lh} {h}} = 0}$ ${\ displaystyle \ lim _ {h \ to 0} {\ frac {f (a + h) -f (a) -Lh} {h}} = 0}$ . Число $L {\ displaystyle L}$ $L$ , когда оно существует, равно $f '(a) {\ displaystyle f' (a)}$ $f'(a)$ .
Существует функция $g: U ⊂ R → R {\ displaystyle g: U \ subset \ mathbb {R} \ to \ mathbb {R}}$ ${\ displaystyle g: U \ subset \ mathbb {R} \ to \ mathbb {R}}$ такой, что $f (a + h) = f ( a) + f ′ (a) h + g (h) {\ displaystyle f (a + h) = f (a) + f '(a) h + g (h)}$ $f(a+h)=f(a)+f'(a)h+g(h)$ и $lim h → 0 g (h) h = 0 {\ displaystyle \ lim _ {h \ to 0} {\ frac {g (h)} {h}} = 0}$ ${\ displaystyle \ lim _ {h \ to 0} {\ frac {g (h)} {h}} = 0}$ .

Дифференцируемость и непрерывность

абсолютное значение функция непрерывна (т.е. не имеет пропусков). Она дифференцируема везде, кроме точки x = 0, где она резко поворачивает, пересекая ось y.

A куспид на графике непрерывной функции. В нуле функция является непрерывной, но не дифференцируемой.

Если f дифференцируема в точке x 0, то f также должна быть непрерывной в точке x 0. В частности, любая дифференцируемая функция должна быть непрерывной в каждой точке своей области определения. Обратное неверно: непрерывная функция не обязательно дифференцируема. Например, функция с изгибом, выступом или вертикальной касательной может быть непрерывной, но не может быть дифференцируемой в месте аномалии.

Большинство функций, которые встречаются на практике, имеют производные во всех точках или в почти в каждой точке. Однако результат Стефана Банаха утверждает, что набор функций, у которых есть производная в некоторой точке, является скудным множеством в пространстве всех непрерывных функций. Неформально это означает, что дифференцируемые функции очень нетипичны среди непрерывных функций. Первым известным примером функции, которая везде непрерывна, но нигде не дифференцируется, является функция Вейерштрасса.

Классы дифференцируемости

Дифференцируемые функции могут быть локально аппроксимированы линейными функциями.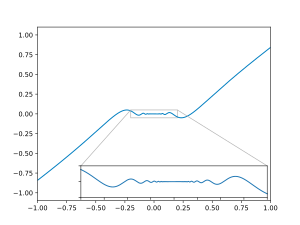

Функция

f: R → R {\ displaystyle f: \ mathbb {R} \ to \ mathbb {R}}

f: \ mathbb {R} \ to \ mathbb {R}

f (x) = x 2 sin ⁡ (1 x) {\ displaystyle f (x) = x ^ {2} \ sin \ left ({\ tfrac {1} {x}} \ right)}

{\ displaystyle f (x) = x ^ {2} \ sin \ left ({\ tfrac {1} {x}} \ right)}

для

x ≠ 0 {\ displaystyle x \ neq 0}

x \ neq 0

f (0) = 0 {\ displaystyle f (0) = 0}

f (0) = 0

дифференцируемо. Однако эта функция не является непрерывно дифференцируемой.

Функция f называется непрерывно дифференцируемой, если производная f '(x) существует и сама является непрерывной функцией. Хотя производная дифференцируемой функции никогда не имеет скачка , у производной может быть существенный разрыв. Например, функция

f (x) = {x 2 sin ⁡ (1 / x), если x ≠ 0 0, если x = 0 {\ displaystyle f (x) \; = \; {\ begin {cases} x ^ {2} \ sin (1 / x) {\ text {if}} x \ neq 0 \\ 0 {\ text {if}} x = 0 \ end {cases}}}

f ( x) \; = \; {\ begin {cases} x ^ {2} \ sin (1 / x) {\ text {if}} x \ neq 0 \\ 0 {\ text {if}} x = 0 \ end {case}}

дифференцируем в 0, поскольку

f '(0) = lim ϵ → 0 (ϵ 2 sin ⁡ (1 / ϵ) - 0 ϵ) = 0, {\ displaystyle f' (0) = \ lim _ {\ epsilon \ to 0} \ left ({\ frac {\ epsilon ^ {2} \ sin (1 / \ epsilon) -0} {\ epsilon}} \ right) = 0,}

f'(0)=\lim _{\epsilon \to 0}\left({\frac {\epsilon ^{2}\sin(1/\epsilon)-0}{\epsilon }}\right)=0,

существует. Однако для x ≠ 0 правила дифференцирования подразумевают, что

f ′ (x) = 2 x sin ⁡ (1 / x) - cos ⁡ (1 / x) {\ displaystyle f '(x) = 2x \ sin (1 / x) - \ cos (1 / x)}

f'(x)=2x\sin(1/x)-\cos(1/x)

, который не имеет предела при x → 0. Тем не менее, теорема Дарбу означает, что производная любой функции удовлетворяет заключению теоремы о промежуточном значении.

Иногда говорят, что непрерывно дифференцируемые функции относятся к классу C. Функция относится к классу C, если первая и вторая производная функции существуют и являются непрерывными. В более общем смысле, функция называется классом C, если все первые k производных f ′ (x), f ′ ′ (x),..., f (x) существуют и непрерывны. Если производные f существуют для всех положительных целых чисел n, функция гладкая или, что эквивалентно, класса C.

Дифференцируемость в более высоких измерениях

A функция нескольких действительных переменных f: R→ Rназывается дифференцируемой. в точке x0, если существует линейное отображение J: R→ Rтакое, что

lim h → 0 ‖ f (x 0 + h) - f (x 0) - J ( час) ‖ р N ‖ час ‖ р м знак равно 0. {\ displaystyle \ lim _ {\ mathbf {h} \ to \ mathbf {0}} {\ frac {\ | \ mathbf {f} (\ mathbf {x_ { 0}} + \ mathbf {h}) - \ mathbf {f} (\ mathbf {x_ {0}}) - \ mathbf {J} \ mathbf {(h)} \ | _ {\ mathbf {R} ^ { n}}} {\ | \ mathbf {h} \ | _ {\ mathbf {R} ^ {m}}}} = 0.}

\ lim _ {\ mathbf {h} \ to \ mathbf {0}} {\ frac {\ | \ mathbf {f} (\ mathbf {x_ {0}} + \ mathbf {h}) - \ mathbf {f} (\ mathbf {x_ {0}}) - \ mathbf {J} \ mathbf {(h)} \ | _ {\ mathbf {R} ^ {n}}} { \ | \ mathbf {h} \ | _ {\ mathbf {R} ^ {m}}}} = 0.

Если функция дифференцируема в x0, то все частные производные существуют в x0, и линейное отображение J задается матрицей Якоби. Аналогичная формулировка многомерной производной обеспечивается фундаментальной леммой приращения, найденной в исчислении с одной переменной.

Если все частные производные функции существуют в окрестности точки x0и непрерывны в точке x0, то функция дифференцируема в этой точке x0.

Однако существование частных производных (или даже всех производных по направлениям ) в общем случае не гарантирует, что функция дифференцируема в точке. Например, функция f: R→ Rопределяется как

f (x, y) = {x if y ≠ x 2 0 if y = x 2 {\ displaystyle f (x, y) = {\ begin {cases } x {\ text {if}} y \ neq x ^ {2} \\ 0 {\ text {if}} y = x ^ {2} \ end {cases}}}

f (x, y) = {\ begin {cases} x {\ text {if}} y \ neq x ^ {2} \\ 0 {\ text {if} } y = x ^ {2} \ end {case}}

не дифференцируемо в (0, 0), но все частные производные и производные по направлению существуют в этой точке. Для непрерывного примера функция

f (x, y) = {y 3 / (x 2 + y 2) if (x, y) ≠ (0, 0) 0 if (x, y) = (0, 0) {\ displaystyle f (x, y) = {\ begin {cases} y ^ {3} / (x ^ {2} + y ^ {2}) {\ text {if}} (x, y) \ neq (0,0) \\ 0 {\ text {if}} (x, y) = (0,0) \ end {ases}}}

f (x, y) = {\ begin {cases} y ^ {3} / (x ^ {2} + y ^ {2}) {\ text {if}} (x, y) \ neq (0,0) \\ 0 {\ text {if}} (x, y) = (0,0) \ end {cases}}

не дифференцируемо в (0, 0), но снова существуют все частные производные и производные по направлению.

Дифференцируемость в комплексном анализе

В комплексном анализе комплексная дифференцируемость определяется с использованием того же определения, что и действительные функции одной переменной. Это допускается возможностью деления комплексных чисел. Итак, функция $f: C → C {\ displaystyle f: \ mathbb {C} \ to \ mathbb {C}}$ ${\ displaystyle f: \ mathbb {C} \ to \ mathbb {C}}$ называется дифференцируемой в $x = a {\ displaystyle x = a}$ $x = a$ , когда

f '(a) = lim h → 0 f (a + h) - f (a) h. {\ displaystyle f '(a) = \ lim _ {h \ to 0} {\ frac {f (a + h) -f (a)} {h}}.}

f'(a)=\lim _{h\to 0}{\frac {f(a+h)-f(a)}{h}}.

Хотя это определение похоже на дифференцируемость вещественных функций с одной переменной, однако это более ограничительное условие. Функция $f: C → C {\ displaystyle f: \ mathbb {C} \ to \ mathbb {C}}$ ${\ displaystyle f: \ mathbb {C} \ to \ mathbb {C}}$ , комплексно-дифференцируемая в точке $x = a { \ displaystyle x = a}$ $x = a$ автоматически дифференцируется в этой точке, если рассматривать его как функцию $f: R 2 → R 2 {\ displaystyle f: \ mathbb {R} ^ {2} \ to \ mathbb {R} ^ {2}}$ ${\ displaystyle f: \ mathbb {R} ^ {2} \ to \ mathbb {R} ^ {2}}$ . Это связано с тем, что из комплексной дифференцируемости следует, что

lim h → 0 | f (a + h) - f (a) - f ′ (a) h | | h | Знак равно 0. {\ Displaystyle \ lim _ {h \ to 0} {\ frac {| f (a + h) -f (a) -f '(a) h |} {| h |}} = 0.}

\lim _{h\to 0}{\frac {|f(a+h)-f(a)-f'(a)h|}{|h|}}=0.

Однако функция $f: C → C {\ displaystyle f: \ mathbb {C} \ to \ mathbb {C}}$ ${\ displaystyle f: \ mathbb {C} \ to \ mathbb {C}}$ может быть дифференцируемой как функция с несколькими переменными, тогда как не быть сложно-дифференцируемым. Например, $f (z) = z + z ¯ 2 {\ displaystyle f (z) = {\ frac {z + {\ overline {z}}} {2}}}$ ${\ displaystyle f (z) = {\ frac {z + {\ overline {z) }}} {2}}}$ дифференцируемо в каждой точке, рассматриваемой как вещественная функция с двумя переменными $f (x, y) = x {\ displaystyle f (x, y) = x}$ $f(x,y)=x$ , но она не является комплексно-дифференцируемой в любой момент.

Любая функция, комплексно-дифференцируемая в окрестности точки, называется голоморфной в этой точке. Такая функция обязательно бесконечно дифференцируема и фактически аналитична.

Дифференцируемые функции на многообразиях

Если M является дифференцируемым многообразием, вещественная или комплекснозначная функция f на M называется дифференцируемой в точке p, если она дифференцируема относительно некоторой (или любой) координатной карты, определенной вокруг точки p. В более общем смысле, если M и N - дифференцируемые многообразия, функция f: M → N называется дифференцируемой в точке p, если она дифференцируема относительно некоторых (или любых) координатных карт, определенных вокруг p и f (p).

Дифференцируемая функция

Содержание

Дифференцируемость вещественных функций одной переменной

Дифференцируемость и непрерывность

Классы дифференцируемости

Дифференцируемость в более высоких измерениях

Дифференцируемость в комплексном анализе

Дифференцируемые функции на многообразиях

См. Также

Ссылки