Теорема о промежуточном значении

редактировать

Непрерывная функция на интервале принимает каждое значение между своими значениями на концах

Теорема о промежуточном значении: пусть f будет непрерывная функция, определенная на [a, b], и пусть s будет числом с f (a) < s < f(b). Then there exists some x between a and b such that f(x) = s.

В математическом анализе теорема о промежуточном значении утверждает, что если f является непрерывная функция, домен которой содержит интервал [a, b], тогда она принимает любое заданное значение между f (a) и f (b) в некоторой точке интервала.

Это имеет два важных следствия :

Если непрерывная функция имеет значения противоположного знака внутри интервала, то она имеет корень в этом интервале (теорема Больцано ).
образ непрерывной функции на интервале сам по себе является интервалом.

Содержание

1 Мотивация
2 Теорема
3 Связь с полнотой
4 Доказательство
5 История
6 Обобщения
7 Converse ложь
8 Практическое применение
9 См. Также
10 Ссылки
11 Внешние ссылки

Мотивация

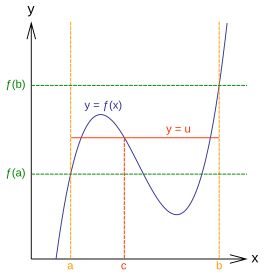Теорема о промежуточном значении

Это отражает интуитивное свойство непрерывных функций над действительными числами : заданная f непрерывна на [1, 2] с известными значениями f (1) = 3 и f (2) = 5. Тогда график y = f (x) должен проходить через горизонтальную линию y = 4, в то время как x перемещается от 1 к 2. Он представляет собой идею о том, что график непрерывной функции на отрезке может быть нарисован, не отрывая карандаша от paper.

Теорема

Теорема о промежуточном значении утверждает следующее:

Рассмотрим интервал $I = [a, b] {\ displaystyle I = [a, b]}$ $I = [a, b]$ вещественных чисел $R {\ displaystyle \ mathbb {R}}$ $\ mathbb {R}$ и непрерывная функция $f: I → R {\ displaystyle f \ двоеточие I \ to \ mathbb {R}}$ $f \ двоеточие I \ к \ R$ . Тогда

Версия I. если $u {\ displaystyle u}$ $u$ - это число от $f (a) {\ displaystyle f (a)}$ $f (a)$ до $f (b) {\ displaystyle f (b)}$ $f (b)$ ,

то есть

min (f (a), f (b)) < u < max ( f ( a), f ( b)) {\displaystyle \min(f(a),f(b))

{\ displaystyle \ min (f (a), f (b)) <u <\ max (f (a), f (b))}

тогда существует a

c ∈ (a, б) {\ displaystyle c \ in (a, b)}

c \ in (a, b)

такой, что

f (c) = u {\ displaystyle f (c) = u}

{\ displaystyle f (c) = u}

Версия II. набор изображений $f (I) {\ displaystyle f (I)}$ $f (I)$ также является интервалом и содержит $[min (f (a), f (б)), макс (е (а), е (б))] {\ Displaystyle {\ bigl [} \ мин (е (а), е (б)), \ макс (е (а), е ( b)) {\ bigr]}}$ ${\ displaystyle {\ bigl [} \ min (f (a), f (b)), \ max (f (a), f (b)) {\ bigr]}}$ ,

Примечание: Версия II утверждает, что набор значений функции не имеет пробелов. Для любых двух значений функции $c < d {\displaystyle c$ $c <d$ , даже если они находятся за пределами интервала между $f (a) {\ displaystyle f (a)}$ $f (a)$ и $f (b) {\ displaystyle f (b)}$ $f (b)$ , все точки в интервале $[c, d] {\ displaystyle {\ bigl [} c, d {\ bigr]}}$ ${\ displaystyle {\ bigl [} c, d {\ bigr]}}$ также являются функциональными значения,

[c, d] ⊆ е (I) {\ displaystyle {\ bigl [} c, d {\ bigr]} \ substeq f (I)}

{\ displaystyle {\ bigl [} c, d {\ bigr]} \ substeq f (I)}

Подмножество действительных чисел без внутренних разрыв - это интервал. Версия I, естественно, содержится в Версии II.

Отношение к полноте

Теорема зависит от полноты действительных чисел и эквивалентна ей. Теорема о промежуточном значении не применяется к рациональным числам ℚ, потому что между рациональными числами существуют промежутки; иррациональные числа заполняют эти пробелы. Например, функция $f (x) = x 2–2 {\ displaystyle f (x) = x ^ {2} -2}$ ${\ displaystyle f (x) = x ^ {2} -2}$ для $x ∈ Q {\ displaystyle x \ in \ mathbb {Q}}$ ${\ displaystyle x \ in \ mathbb {Q}}$ удовлетворяет $f (0) = - 2 {\ displaystyle f (0) = - 2}$ ${\ displaystyle f (0) = - 2}$ и $f (2) Знак равно 2 {\ Displaystyle F (2) = 2}$ ${\ displaystyle f (2) = 2}$ . Однако не существует рационального числа $x {\ displaystyle x}$ $x$ такого, что $f (x) = 0 {\ displaystyle f (x) = 0}$ $f (x) = 0$ , потому что $2 {\ displaystyle {\ sqrt {2}}}$ ${\ sqrt {2}}$ - иррациональное число.

Доказательство

Теорема может быть доказана как следствие свойства полноты вещественных чисел следующим образом:

Мы докажем первый случай, $f (a) < u < f ( b) {\displaystyle f(a)$ ${\ displ aystyle f (a) <u <f (b)}$ . Второй случай аналогичен.

Пусть $S {\ displaystyle S}$ $S$ будет набором всех $x ∈ [a, b] {\ displaystyle x \ in [a, b]}$ $x \ in [a, b]$ такое, что $f (x) ≤ u {\ displaystyle f (x) \ leq u}$ ${\ displaystyle f (x) \ leq u}$ . Тогда $S {\ displaystyle S}$ $S$ не является пустым, поскольку $a {\ displaystyle a}$ $a$ является элементом $S {\ displaystyle S}$ $S$ , а $S {\ displaystyle S}$ $S$ ограничен сверху $b {\ displaystyle b}$ $b$ . Следовательно, по полноте существует supremum $c = sup S {\ displaystyle c = \ sup S}$ ${\ displaystyle c = \ sup S}$ . То есть $c {\ displaystyle c}$ $c$ - это наименьшее число, которое больше или равно каждому члену $S {\ displaystyle S}$ $S$ . Мы утверждаем, что $f (c) = u {\ displaystyle f (c) = u}$ ${\ displaystyle f (c) = u}$ .

Fix some $ε>0 {\ displaystyle \ varepsilon>0}$ $\varepsilon>0$ . Начиная с $f {\ displaystyle f}$ $f$ непрерывно, существует $δ>0 {\ displaystyle \ delta>0}$ $\delta>0$ такой, что $| f (x) - f (c) | < ε {\displaystyle |f(x)-f(c)|<\varepsilon }$ ${\ displaystyle | f (x) -f (c) | <\ varepsilon}$ всякий раз, когда $| х - с | < δ {\displaystyle |x-c|<\delta }$ ${\ displaystyle | xc | <\ delta}$ . Это означает, что

f (x) - ε < f ( c) < f ( x) + ε {\displaystyle f(x)-\varepsilon

{\ displaystyle f (x) - \ varepsilon <f (c) <f (x) + \ varepsilon}

для всех $x ∈ (c - δ, c + δ) {\ displaystyle x \ in (c- \ delta, c + \ delta)}$ ${\ displaystyle x \ in (c- \ delta, c + \ delta)}$ . По свойствам супремума существует $a ∗ ∈ (c - δ, c] {\ displaystyle a ^ {*} \ in (c- \ delta, c]}$ ${\ displaystyle a ^ {*} \ in (c- \ delta, c]}$ то есть содержится в $S {\ displaystyle S}$ $S$ , и поэтому

f (c) < f ( a ∗) + ε ≤ u + ε {\displaystyle f(c)

{\ displaystyle f (c) <f (a ^ { *}) + \ varepsilon \ leq u + \ varepsilon}

Выбор $a ∗ ∗ ∈ (c, c + δ) {\ displaystyle a ^ {**} \ in (c, c + \ delta)}$ ${\ displaystyle a ^ {**} \ in (c, c + \ delta)}$ , мы знаем, что $a ∗ ∗ ∉ S {\ displaystyle a ^ {**} \ not \ in S}$ ${\ displaystyle a ^ {**} \ not \ in S}$ потому что $c {\ displaystyle c}$ $c$ является верхней гранью $S {\ displaystyle S}$ $S$ . Это означает, что

f (c)>е (a ∗ ∗) - ε>u - ε {\ displaystyle f (c)>f (a ^ {**}) - \ varepsilon \>u- \ varepsilon}

f(c)>f (a ^ { **}) - \ varepsilon \>u- \ varepsilon

Оба неравенства

u - ε < f ( c) < u + ε {\displaystyle u-\varepsilon

{\ displaystyle u - \ varepsilon <е (с) <u + \ varepsilon}

действительны для всех $ε>0 {\ displaystyle \ varepsilon>0}$ $\varepsilon>0$ , из которого мы выводим $f (c) = u {\ displaystyle f (c) = u}$ ${\ displaystyle f (c) = u}$ как единственно возможное значение, как указано.

Примечание: Теорема о промежуточном значении также может быть доказана с использованием методов нестандартного анализа, который ставит «интуитивные» аргументы, включающие бесконечно малые величины, на строгую основу.

История

Для u = 0 выше утверждение также известно как теорема Больцано. (Поскольку в u = 0 нет ничего особенного, это, очевидно, эквивалентно самой теореме о промежуточном значении.) Эта теорема была впервые доказана Бернаром Больцано в 1817 году. Огюстен-Луи Коши предоставил доказательство в 1821 году. Оба были вдохновлены целью формализовать анализ функций и работой Жозефа-Луи Лагранжа. Идея о том, что непрерывные функции обладают свойством промежуточного значения, имеет более раннее происхождение. Саймон Стевин доказал теорему о промежуточном значении для многочленов (на примере кубической ), предоставив алгоритм построения десятичного разложения решения. Алгоритм итеративно делит интервал на 10 частей, создавая дополнительную десятичную цифру на каждом шаге итерации. До того, как было дано формальное определение непрерывности, свойство промежуточного значения было дано как часть определения непрерывной функции. Среди сторонников - Луи Арбогаст, который предположил, что функции не имеют скачков, удовлетворяют свойству промежуточного значения и имеют приращения, размеры которых соответствуют размерам приращений переменной. Ранее авторы считали результат интуитивно очевидным и не требующим доказательств. Идея Больцано и Коши состояла в том, чтобы определить общее понятие непрерывности (в терминах бесконечно малых в случае Коши и с использованием действительных неравенств в случае Больцано) и предоставить доказательство, основанное на таких определениях.

Обобщения

Теорема о промежуточном значении тесно связана с топологическим понятием связности и следует из основных свойств связных множеств в метрических пространствах. и, в частности, связанные подмножества ℝ:

Если $X {\ displaystyle X}$ $X$ и $Y {\ displaystyle Y}$ $Y$ являются метрическими пространствами, $f: X → Y {\ displaystyle f \ двоеточие X \ to Y}$ $f \ двоеточие X \ to Y$ - непрерывная карта, а $E ⊂ X {\ displaystyle E \ subset X}$ ${\ displaystyle E \ subset X}$ - это подключенное подмножество, тогда подключается $f (E) {\ displaystyle f (E)}$ ${\ displaystyle f (E)}$ . (*)
Подмножество $E ⊂ R {\ displaystyle E \ subset \ mathbb {R}}$ $E \ subset \ mathbb {R}$ связано тогда и только тогда, когда оно удовлетворяет следующему свойству: $x, y ∈ E, x < r < y ⟹ r ∈ E {\displaystyle x,y\in E,\ x$ ${\ displaystyle x, y \ in E, \ x <r <y \ подразумевает r \ in E}$ . (**)

Фактически связность - это топологическое свойство, и (*) обобщается на топологические пространства : Если $X {\ displaystyle X}$ $X$ и $Y {\ displaystyle Y}$ $Y$ - топологические пространства, $f: X → Y {\ displaystyle f \ двоеточие X \ to Y}$ $f \ двоеточие X \ to Y$ - непрерывное карта, а $X {\ displaystyle X}$ $X$ - связанное пространство, тогда $f (X) {\ displaystyle f (X)}$ $f (X)$ связано. Сохранение связности при непрерывных отображениях можно рассматривать как обобщение теоремы о промежуточном значении, свойства вещественнозначных функций действительной переменной, на непрерывные функции в общих пространствах.

Вспомните первую версию теоремы о промежуточном значении, изложенную ранее:

Теорема о промежуточном значении. (Версия I). Рассмотрим отрезок $I = [a, b] {\ displaystyle I = [a, b]}$ $I = [a, b]$ в вещественных числах $R {\ displaystyle \ mathbb {R}}$ $\ mathbb {R}$ и непрерывная функция $f: I → R {\ displaystyle f \ двоеточие I \ to \ mathbb {R}}$ ${\ displaystyle f \ двоеточие I \ to \ mathbb {R}}$ . Тогда, если $u {\ displaystyle u}$ $u$ является действительным числом такое, что $min (f (a), f (b)) < u < max ( f ( a), f ( b)) {\displaystyle \min(f(a),f(b))$ ${\ displaystyle \ min (f (a), f (b)) <u <\ max (f (a), f (b))}$ , существует $c ∈ (a, b) {\ displaystyle c \ in (a, b)}$ $c \ in (a, b)$ так, что $f (c) = u {\ displaystyle f (c) = u}$ ${\ displaystyle f (c) = u}$ .

промежуточное значение Теорема является непосредственным следствием этих двух свойств связности:

Доказательство: По (**), $I = [a, b] {\ displaystyle I = [a, b]}$ $I = [a, b]$ - это подключенный набор. Из (*) следует, что изображение $f (I) {\ displaystyle f (I)}$ $f (I)$ также связано. Для удобства предположим, что $f (a) < f ( b) {\displaystyle f(a)$ ${\ displaystyle f (a) <f (b)}$ . Затем еще раз вызов (**), $f (a) < u < f ( b) {\displaystyle f(a)$ ${\ displ aystyle f (a) <u <f (b)}$ означает, что $u ∈ f (I) {\ displaystyle u \ in f (I)}$ ${\ displaystyle u \ in f (I)}$ , или $е (с) = u {\ displaystyle f (c) = u}$ ${\ displaystyle f (c) = u}$ для некоторого $c ∈ I {\ displaystyle c \ in I}$ ${\ displaystyle c \ в I}$ . Поскольку $U ≠ е (a), е (b) {\ displaystyle u \ neq f (a), f (b)}$ ${\ displaystyle u \ neq f (a), f (b)}$ , $c ∈ (a, b) {\ displaystyle c \ in (a, б)}$ $c \ in (a, b)$ должен действительно выполняться, и из этого следует желаемый вывод. Тот же аргумент применим, если $f (b) < f ( a) {\displaystyle f(b)$ ${\ displaystyle f (b) <f (a)}$ , так что все готово. $◼ {\ displaystyle \ \ \ blacksquare}$ ${\ displaystyle \ \ \ blacksquare}$

Теорема о промежуточном значении обобщается естественным образом: предположим, что X есть связное топологическое пространство и (Y, <) is a полностью упорядоченное множество, снабженное топологией порядка , и пусть f: X → Y - непрерывное отображение. Если a и b - две точки в X и u - точка в Y, лежащая между f (a) и f (b) относительно <, то существует c в X такое, что f (c) = u. Исходная теорема восстанавливается, если заметить, что ℝ связно и что его естественная топология является топологией порядка.

Теорема Брауэра о неподвижной точке является связанной теоремой, которая в одном измерении дает частный случай промежуточного Теорема о значении.

Converse is false

A Функция Дарбу - это функция f с действительными значениями, которая имеет «свойство промежуточного значения», т. е. удовлетворяет заключению теоремы о промежуточном значении: для любого два значения a и b в области o f f, и любой y между f (a) и f (b), существует некоторый c между a и b с f (c) = y. Теорема о промежуточном значении утверждает, что каждая непрерывная функция является функцией Дарбу. Однако не всякая функция Дарбу непрерывна; т.е. обратное утверждение теоремы о промежуточном значении неверно.

В качестве примера возьмем функцию f: [0, ∞) → [−1, 1], определенную формулой f (x) = sin (1 / x) для x>0 и f (0) = 0. Эта функция не является непрерывной при x = 0, поскольку предел для f (x), когда x стремится к 0, не существует; но функция имеет свойство промежуточного значения. Другой, более сложный пример дается функцией с основанием 13 Конвея.

Фактически, теорема Дарбу утверждает, что все функции, которые являются результатом дифференцирования какой-либо другой функции на некоторые интервалы имеют свойство промежуточного значения (даже если они не обязательно должны быть непрерывными).

Исторически это свойство промежуточного значения предлагалось как определение непрерывности функций с действительным знаком; это определение не было принято.

Практическое применение

Аналогичным результатом является теорема Борсука – Улама, в которой говорится, что непрерывная карта из $n {\ displaystyle n}$ $n$ -сфера в евклидово $n {\ displaystyle n}$ $n$ -пространство всегда будет отображать некоторые пары противоположных точек в одно и то же место.

Доказательство для одномерного случая: возьмем $f {\ displaystyle f}$ $f$ как любую непрерывную функцию на окружности. Проведите линию через центр круга, пересекая его в двух противоположных точках $A {\ displaystyle A}$ $A$ и $B {\ displaystyle B}$ $B$ . Определите $d {\ displaystyle d}$ $d$ как $f (A) - f (B) {\ displaystyle f (A) -f (B)}$ ${\ displaystyle f (A) -f (B)}$ . Если линия повернута на 180 градусов, вместо нее будет получено значение -d. Согласно теореме о промежуточном значении должен быть некоторый промежуточный угол поворота, для которого d = 0, и, как следствие, f (A) = f (B) под этим углом.

В общем, для любой непрерывной функции, область определения которой является некоторой замкнутой выпуклой $n {\ displaystyle n}$ $n$ -мерной формой и любой точкой внутри формы (не обязательно ее центром), относительно данной точки существуют две антиподальные точки, функциональное значение которых одинаково.

Теорема также подкрепляет объяснение того, почему вращение шаткого стола приводит к его устойчивости (с учетом некоторых легко выполняемых ограничений).

См. Также

Ссылки

Внешние ссылки

Теорема о промежуточном значении в ProofWiki
Теорема о промежуточном значении - теорема Больцано в разрубить узел
Больцано Теорема Хулио Сезара де ла Инсера, Wolfram Demonstrations Project.
Вайсштейн, Эрик У. «Теорема о промежуточном значении». MathWorld.
Белк, Джим (2 января 2012 г.). «Двумерная версия теоремы о промежуточном значении». Обмен стеками.
Система Mizar подтверждение: http://mizar.org/version/current/html/topreal5.html#T4