Функция Кантора

редактировать

Непрерывная функция, которая не является абсолютно непрерывной

График функции Кантора на единичном интервале

В математика, функция Кантора является примером функции, которая является непрерывной, но не абсолютно непрерывной. Это печально известный контрпример в анализе, потому что он бросает вызов наивным интуициям о непрерывности, производной и мере. Хотя она всюду непрерывна и почти везде имеет нулевую производную, ее значение все равно изменяется от 0 до 1, когда ее аргумент достигает от 0 до 1. Таким образом, в одном смысле функция кажется очень похожей на постоянную, которая не может расти, а в другом., она действительно монотонно растет по построению.

Она также называется троичной функцией Кантора, функцией Лебега, сингулярной функцией Лебега, функцией Кантора – Витали функция, Лестница Дьявола, лестница Кантора и функция Кантора – Лебега . Георг Кантор (1884) представил функцию Кантора и упомянул, что Шеффер указал, что это контрпример к расширению фундаментальной теоремы исчисления, заявленной Гарнаком. Функция Кантора обсуждалась и популяризировалась Шеффером (1884), Лебегом (1904) и Витали (1905).

Содержание

1 Определение
2 Свойства
- 2.1 Отсутствие абсолютной непрерывности
3 Альтернативные определения
- 3.1 Итерационное построение
- 3.2 Фрактальный объем
4 Самоподобие
5 Обобщения
6 См. Также
7 Примечания
8 Ссылки
9 Внешние ссылки

Определение

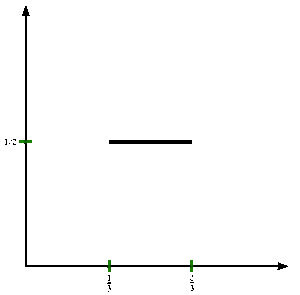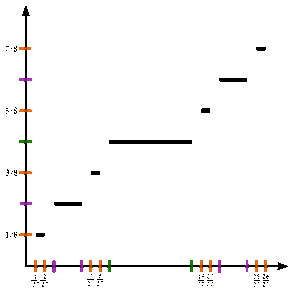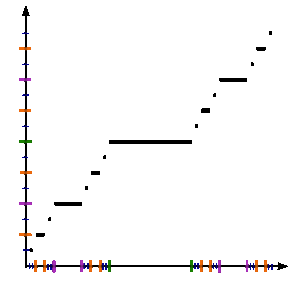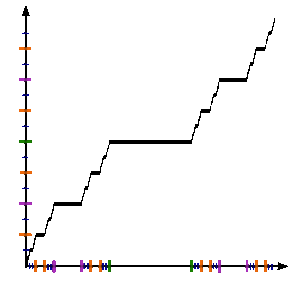
См. Рисунок. Чтобы формально определить функцию Кантора c: [0,1] → [0,1], пусть x находится в [0,1] и получите c (x) с помощью следующих шагов:

Выразите x по основанию 3.
Если x содержит 1, замените каждую цифру строго после первой 1 на 0.
Замените любые оставшиеся 2 на 1.
Интерпретируйте результат как двоичное число. Результат - c (x).

Например:

1/4 равно 0,02020202... в базе 3. Единиц нет, поэтому следующий этап по-прежнему равен 0,02020202... Это переписывается как 0,01010101... При чтении по основанию 2 это соответствует 1/3, поэтому c (1/4) = 1/3.
1/5 равно 0,01210121... по основанию 3. Цифры после первой 1 заменяются на 0, чтобы получить 0,01000000... Это не переписывается, так как двоек нет. При чтении по основанию 2 это соответствует 1/4, поэтому c (1/5) = 1/4.
200/243 равно 0,21102 (или 0,211012222...) по основанию 3. Цифры после первая 1 заменяется на 0, чтобы получить 0,21. Это переписано как 0.11. При чтении по основанию 2 это соответствует 3/4, поэтому c (200/243) = 3/4.

Эквивалентно, если $C {\ displaystyle {\ mathcal {C}}}$ ${\ mathcal {C}}$ - это множество Кантора на [0,1], тогда функция Кантора c: [0,1] → [0,1] может быть определена как

c (x) = {∑ n = 1 ∞ an 2 n, x = ∑ n = 1 ∞ 2 an 3 n ∈ C foran ∈ {0, 1}; sup y ≤ x, y ∈ C c (y), x ∈ [0, 1] ∖ C. {\ displaystyle c (x) = {\ begin {cases} \ sum _ {n = 1} ^ {\ infty} {\ frac {a_ {n}} {2 ^ {n}}}, x = \ sum _ {n = 1} ^ {\ infty} {\ frac {2a_ {n}} {3 ^ {n}}} \ in {\ mathcal {C}} \ \ mathrm {for} \ a_ {n} \ in \ {0,1 \}; \\\ sup _ {y \ leq x, \, y \ in {\ mathcal {C}}} c (y), x \ in [0,1] \ setminus {\ mathcal { C}}. \\\ end {cases}}}

{\ displaystyle c (x) = {\ begin {cases} \ sum _ {n = 1} ^ {\ infty} {\ frac {a_ {n}} {2 ^ {n}}}, x = \ sum _ {n = 1} ^ {\ infty} {\ frac {2a_ {n}} {3 ^ {n}}} \ in {\ mathcal {C}} \ \ mathrm {for} \ a_ {n} \ in \ {0,1 \}; \\\ sup _ {y \ leq x, \, y \ in {\ mathcal {C}}} c (y), x \ in [0,1] \ setminus {\ mathcal { C}}. \\\ end {case}}}

Эта формула хорошо определена, поскольку каждый член набора Кантора имеет уникальное представление базы 3, которое содержит только цифры 0 или 2. (Для некоторых членов набора Кантора $C {\ displaystyle {\ mathcal {C}}}$ ${\ mathcal {C}}$ , троичное расширение повторяется с замыкающими двойками, и есть альтернативное неповторяющееся расширение, заканчивающееся на 1. Например, 1/3 = 0,1 3 = 0,02222... 3 является членом множества Кантора). Поскольку c (0) = 0 и c (1) = 1, а c является монотонным на $C {\ displaystyle {\ mathcal {C}}}$ ${\ mathcal {C}}$ , ясно, что 0 ≤ c ( x) ≤ 1 также выполняется для всех $x ∈ [0, 1] ∖ C {\ displaystyle x \ in [0,1] \ setminus {\ mathcal {C}}}$ ${\ displaystyle x \ in [0,1] \ setminus {\ mathcal {C}}}$ .

Свойства

Функция Кантора бросает вызов наивной интуиции о непрерывности и мере ; хотя он всюду непрерывен и имеет нулевую производную почти всюду, $c (x) {\ textstyle c (x)}$ ${\ textstyle c (x)}$ изменяется от 0 до 1 как $x { \ textstyle x}$ ${\ textstyle x}$ изменяется от 0 до 1 и принимает все значения между ними. Функция Кантора является наиболее часто цитируемым примером вещественной функции, которая равномерно непрерывна (точнее, она непрерывна по Гёльдеру степени α = log 2 / log 3), но не абсолютно непрерывный. Постоянно на интервалах вида (0.x 1x2x3... x n 022222..., 0.x 1x2x3... x n 200000...), и каждая точка, не входящая в множество Кантора, находится в одном из этих интервалов, поэтому ее производная равна 0 вне множества Кантора. С другой стороны, он не имеет производной в любой точке несчетного подмножества набора Кантора, содержащего конечные точки интервала, описанные выше.

Функцию Кантора также можно рассматривать как кумулятивную функцию распределения вероятностей 1 / 2-1 / 2 меры Бернулли μ, поддерживаемой на множестве Кантора: $с (х) = μ ([0, x]) {\ textstyle c (x) = \ mu ([0, x])}$ ${\ textstyle c (x) = \ му ([0, x])}$ . Это распределение вероятностей, называемое распределением Кантора, не имеет дискретной части. То есть соответствующая мера безатомная. Поэтому в функции отсутствуют скачкообразные скачки функции; любой такой скачок соответствовал бы атому в мере.

Однако никакая непостоянная часть функции Кантора не может быть представлена в виде интеграла от функции плотности вероятности ; интегрирование любой предполагаемой функции плотности вероятности, которая не почти всюду нулем на любом интервале, даст положительную вероятность некоторому интервалу, которому это распределение присваивает нулевую вероятность. В частности, как указал Виталий (1905), функция не является интегралом своей производной, хотя производная существует почти везде.

Функция Кантора является стандартным примером сингулярной функции.

Функция Кантора неубывающая, и поэтому, в частности, ее график определяет спрямляемую кривую. Scheeffer (1884) показал, что длина дуги его графика равна 2.

Отсутствие абсолютной непрерывности

Поскольку мера Лебега несчетно бесконечное множество Кантора равно 0, для любого положительного ε < 1 and δ, there exists a finite sequence of попарно непересекающихся подинтервалов с общей длиной < δ over which the Cantor function cumulatively rises more than ε.

Фактически, для любого δ>0 существует конечное число много попарно непересекающихся интервалов (x k,yk) (1 ≤ k ≤ M) с $∑ k = 1 M (yk - xk) < δ {\displaystyle \sum \limits _{k=1}^{M}(y_{k}-x_{k})<\delta }$ ${\ displaystyle \ сумма \ пределы _ {k = 1} ^ {M} (y_ {k} -x_ {k}) <\ delta}$ и $∑ k = 1 M (c (yk) - c (xk)) = 1 {\ displaystyle \ sum \ limits _ {k = 1} ^ {M} (c (y_ {k}) - c (x_ {k})) = 1}$ ${\ displaystyle \ sum \ limits _ {к = 1} ^ {M} (c (y_ {k}) - c (x_ {k})) = 1}$ .

Альтернативные определения

Итерационное построение

Ниже мы определяем последовательность {f n } функций на единичном интервале, которая сходится к функции Кантора.

Пусть f 0 (x) = x.

Тогда для каждого целого числа n ≥ 0 следующая функция f n + 1 (x) будет определена в терминах f n (x) следующим образом :

Пусть f n + 1 (x) = 1/2 × f n (3x), когда 0 ≤ x ≤ 1/3;

Пусть f n + 1 (x) = 1/2, когда 1/3 ≤ x ≤ 2/3;

Пусть f n + 1 (x) = 1/2 + 1/2 × f n (3 x - 2), когда 2/3 ≤ x ≤ 1.

Три определения совместимы в конечных точках 1/3 и 2/3, потому что f n (0) = 0 и f n (1) = 1 для любого n по индукции. Можно проверить, что f n поточечно сходится к функции Кантора, определенной выше. Кроме того, сходимость равномерная. Действительно, разделив на три случая, согласно определению f n + 1, мы увидим, что

max x ∈ [0, 1] | f n + 1 (x) - f n (x) | ≤ 1 2 max x ∈ [0, 1] | f n (x) - f n - 1 (x) |, п ≥ 1. {\ Displaystyle \ макс _ {х \ в [0,1]} | f_ {n + 1} (x) -f_ {n} (x) | \ leq {\ frac {1} {2 }} \, \ max _ {x \ in [0,1]} | f_ {n} (x) -f_ {n-1} (x) |, \ quad n \ geq 1.}

\ max_ {x \ in [0, 1]} | f_ {n + 1} (x) - f_n (x) | \ le \ frac 1 2 \, \ max_ {x \ in [0, 1]} | f_ {n} (x) - f_ {n-1} (x) |, \ quad n \ ge 1.

Если f обозначает предельную функцию, то для любого n ≥ 0

max x ∈ [0, 1] | f (x) - f n (x) | ≤ 2 - n + 1 max x ∈ [0, 1] | f 1 (x) - f 0 (x) |. {\ displaystyle \ max _ {x \ in [0,1]} | f (x) -f_ {n} (x) | \ leq 2 ^ {- n + 1} \, \ max _ {x \ in [ 0,1]} | f_ {1} (x) -f_ {0} (x) |.}

\ max_ {x \ in [0, 1]} | f (x) - f_n (x) | \ le 2 ^ {- n + 1} \, \ max_ {x \ in [0, 1]} | f_1 (x) - f_0 (x) |.

Также выбор начальной функции не имеет большого значения, если f 0 (0) = 0, f 0 (1) = 1 и f 0 ограничено.

Фрактальный объем

Функция Кантора тесно связана с набор Кантора. Множество Кантора C можно определить как набор тех чисел в интервале [0, 1], которые не содержат цифры 1 в их разложении по основанию 3 (триаду), за исключением случаев, когда следует 1 только нулями (в этом случае хвост 1000 $… {\ displaystyle \ ldots}$ $\ ldots$ можно заменить на 0222 $… {\ displaystyle \ ldots}$ $\ ldots$ , чтобы избавиться любого 1). Оказывается, множество Кантора - это фрактал с (несчетным) бесконечным количеством точек (нульмерный объем), но нулевой длины (одномерный объем). Только D-мерный объем $HD {\ displaystyle H_ {D}}$ $H_D$ (в смысле меры Хаусдорфа ) принимает конечное значение, где $D = журнал ⁡ (2) / журнал ⁡ (3) {\ displaystyle D = \ log (2) / \ log (3)}$ $D = \ log (2) / \ log (3)$ - фрактальная размерность C. Мы можем определить функцию Кантора как альтернативу D-мерный объем сечений канторовского множества

f (x) = HD (C ∩ (0, x)). {\ displaystyle f (x) = H_ {D} (C \ cap (0, x)).}

f (x) = H_D (C \ cap (0, x)).

Самоподобие

Функция Кантора обладает несколькими симметриями . Для $0 ≤ x ≤ 1 {\ displaystyle 0 \ leq x \ leq 1}$ $0 \ leq x \ leq 1$ существует симметрия отражения

c (x) = 1 - c (1 - x) {\ displaystyle c (x) = 1-c (1-x)}

{\ displaystyle c (x) = 1-c (1-x)}

и пара увеличений, одно слева и одно справа:

c (x 3) = c (x) 2 {\ displaystyle c \ left ({\ frac {x} {3}} \ right) = {\ frac {c (x)} {2}}}

{\ displaystyle c \ left ({\ frac {x} {3}} \ right) = {\ frac {c (x)} {2}}}

c (x + 2 3) = 1 + c (x) 2 {\ displaystyle c \ left ({\ frac {x + 2} {3}} \ right) = {\ frac {1 + c (x)} {2}}}

{\ displaystyle c \ left ({\ frac {x + 2} {3}} \ right) = {\ frac {1 + c (x)} {2}}}

Увеличение может быть каскадным; они порождают диадический моноид. Это демонстрируется определением нескольких вспомогательных функций. Определите отражение как

r (x) = 1 - x {\ displaystyle r (x) = 1-x}

{\ displaystyle r ( x) = 1-x}

Первая самосимметрия может быть выражена как

r ∘ c = c ∘ r { \ displaystyle r \ circ c = c \ circ r}

{\ displaystyle r \ circ c = c \ circ r}

, где символ $∘ {\ displaystyle \ circ}$ $\ circ$ обозначает композицию функций. То есть $(р ∘ c) (x) = r (c (x)) = 1 - c (x) {\ displaystyle (r \ circ c) (x) = r (c (x)) = 1-c (x)}$ ${\ displaystyle (r \ circ c) (x) = r (c (x)) = 1-c (x)}$ и аналогично для других случаев. Для левого и правого увеличения запишите левые отображения

LD (x) = x 2 {\ displaystyle L_ {D} (x) = {\ frac {x} {2}}}

{\ displaystyle L_ {D} (x) = {\ frac {x} {2}}}

LC (x) = x 3 {\ displaystyle L_ {C} (x) = {\ frac {x} {3}}}

{\ displaystyle L_ {C} (x) = {\ frac {x} {3}}}

Тогда функция Кантора подчиняется

LD ∘ c = c ∘ LC {\ displaystyle L_ {D} \ circ c = c \ circ L_ {C}}

{\ displaystyle L_ {D} \ circ c = c \ circ L_ {C}}

Аналогичным образом определите правые сопоставления как

RD (x) = 1 + x 2 {\ displaystyle R_ {D} ( x) = {\ frac {1 + x} {2}}}

{\ displaystyle R_ {D} (x) = {\ frac {1+ x} {2}}}

RC (x) = 2 + x 3 {\ displaystyle R_ {C} (x) = {\ frac { 2 + x} {3}}}

{ \ displaystyle R_ {C} (x) = {\ frac {2 + x} {3}}}

Тогда аналогично,

RD ∘ c = c ∘ RC {\ displaystyle R_ {D} \ circ c = c \ circ R_ {C}}

{\ displaystyle R_ {D} \ circ c = c \ circ R_ {C}}

Два стороны могут быть отражены одна на другую, так как

LD ∘ r = r ∘ RD {\ displaystyle L_ {D} \ circ r = r \ circ R_ {D}}

{\ displaystyle L_ {D} \ circ r = r \ circ R_ {D}}

и аналогично,

LC ∘ r = r ∘ RC {\ displaystyle L_ {C} \ circ r = r \ circ R_ {C}}

{\ displaystyle L_ {C} \ circ r = r \ circ R_ {C}}

Эти операции можно складывать произвольно. Рассмотрим, например, последовательность движений влево-вправо $L R L L R. {\ displaystyle LRLLR.}$ ${\ displaystyle LRLLR.}$ Добавление индексов C и D и, для ясности, удаление оператора композиции $∘ {\ displaystyle \ circ}$ $\ circ$ во всех местах, кроме нескольких, один имеет:

LDRDLDLDRD ∘ c = c ∘ LCRCLCLCRC {\ displaystyle L_ {D} R_ {D} L_ {D} L_ {D} R_ {D} \ circ c = c \ circ L_ {C} R_ { C} L_ {C} L_ {C} R_ {C}}

{\ displaystyle L_ {D} R_ {D} L_ {D} L_ {D} R_ {D} \ circ c = c \ circ L_ {C} R_ {C} L_ {C } L_ {C} R_ {C}}

Произвольные строки конечной длины в буквах L и R соответствуют диадическим рациональным числам, в том смысле, что каждое диадическое рациональное число может быть записано как как $y = n / 2 m {\ displaystyle y = n / 2 ^ {m}}$ ${\ displaystyle y = n / 2 ^ {m}}$ для целых n и m и как конечная длина битов $y = 0. b 1 b 2 b 3 ⋯ bm {\ displaystyle y = 0.b_ {1} b_ {2} b_ {3} \ cdots b_ {m}}$ ${\ displaystyle y = 0.b_ {1} b_ {2} b_ {3} \ cdots b_ {m}}$ с $bk ∈ {0, 1}. {\ displaystyle b_ {k} \ in \ {0,1 \}.}$ ${\ displaystyle b_ {k} \ in \ {0,1 \}.}$ Таким образом, каждое диадическое рациональное соответствие находится во взаимно однозначном соответствии с некоторой самосимметрией функции Кантора.

Некоторые изменения в обозначениях могут облегчить выражение вышеизложенного. Пусть $g 0 {\ displaystyle g_ {0}}$ $g_ {0}$ и $g 1 {\ displaystyle g_ {1}}$ $g_ {1}$ обозначают L и R. Функциональная композиция расширяет это в моноид, в котором можно записать $g 010 = g 0 g 1 g 0 {\ displaystyle g_ {010} = g_ {0} g_ {1} g_ {0}}$ ${\ displaystyle g_ {010} = g_ {0} g_ { 1} g_ {0}}$ и, как правило, $g A g B = g AB {\ displaystyle g_ {A} g_ {B} = g_ {AB}}$ ${\ displaystyle g_ {A} g_ {B} = g_ {AB }}$ для некоторых двоичных строк цифр A, B, где AB - это обычное конкатенация таких строк. Тогда диадический моноид M является моноидом всех таких лево-правых ходов конечной длины. Записывая $γ ∈ M {\ displaystyle \ gamma \ in M}$ ${\ displaystyle \ gamma \ in M}$ как общий элемент моноида, мы получаем соответствующую самосимметрию функции Кантора:

γ D ∘ c = c ∘ γ C {\ displaystyle \ gamma _ {D} \ circ c = c \ circ \ gamma _ {C}}

{\ displaystyle \ gamma _ {D} \ circ c = c \ circ \ gamma _ {C}}

Сам диадический моноид имеет несколько интересных свойств. Его можно рассматривать как конечное число движений влево-вправо вниз по бесконечному двоичному дереву ; бесконечно удаленные «листья» на дереве соответствуют точкам на множестве Кантора, и, таким образом, моноид также представляет самосимметрии множества Кантора. Фактически, большой класс часто встречающихся фракталов описывается диадическим моноидом; дополнительные примеры можно найти в статье о кривых де Рама. Другие фракталы, обладающие самоподобием, описываются с другими видами моноидов. Диадический моноид сам по себе является субмоноидом модульной группы $S L (2, Z). {\ displaystyle SL (2, \ mathbb {Z}).}$ ${\ displaystyle SL (2, \ mathbb {Z}).}$

Обратите внимание, что функция Кантора имеет более чем мимолетное сходство с функцией вопросительного знака Минковского. В частности, он подчиняется точно таким же соотношениям симметрии, хотя и в измененной форме.

Обобщения

Пусть

y = ∑ k = 1 ∞ bk 2 - k {\ displaystyle y = \ sum _ {k = 1} ^ {\ infty} b_ {k} 2 ^ {- k}}

y = \ sum_ {k = 1} ^ \ infty b_k 2 ^ { -k}

быть диадическим (двоичным) разложением действительного числа 0 ≤ y ≤ 1 в виде двоичных цифр b k ∈ {0,1 }. Это расширение обсуждается более подробно в статье о диадическом преобразовании . Затем рассмотрим функцию

C z (y) = ∑ k = 1 ∞ b k z k. {\ displaystyle C_ {z} (y) = \ sum _ {k = 1} ^ {\ infty} b_ {k} z ^ {k}.}

C_z (y) = \ sum_ {k = 1} ^ \ infty b_k z ^ {k}.

Для z = 1/3 функция, обратная x = 2 C 1/3 (y) - функция Кантора. То есть y = y (x) - функция Кантора. В общем, для любого z < 1/2, Cz (y) выглядит так, как будто функция Кантора повернута на бок, при этом ширина ступенек увеличивается по мере приближения z к нулю.

Как упоминалось выше, функция Кантора также является кумулятивной функцией распределения меры на множестве Кантора. Различные функции Кантора или лестницы Дьявола могут быть получены путем рассмотрения различных безатомных вероятностных мер, поддерживаемых на множестве Кантора или других фракталах. В то время как функция Кантора почти везде имеет производную 0, текущие исследования сосредоточены на вопросе размера набора точек, в которых правая верхняя производная отличается от правой нижней производной, в результате чего производная не существует. Этот анализ дифференцируемости обычно дается в терминах фрактальной размерности, причем размерность Хаусдорфа наиболее популярна. Это направление исследований было начато в 1990-х Дарстом, который показал, что размерность Хаусдорфа множества недифференцируемости функции Кантора является квадратом размерности множества Кантора, $(log ⁡ 2 / log ⁡ 3) 2 {\ displaystyle (\ log 2 / \ log 3) ^ {2}}$ ${\ displaystyle (\ log 2 / \ log 3) ^ { 2}}$ . Впоследствии Фальконер показал, что это соотношение возведения в квадрат выполняется для всех регулярных сингулярных мер Альфора, т.е.

dim H ⁡ {x: f ′ (x) = lim h → 0 + μ ([x, x + час]) час не существует} = (тусклый H ⁡ supp ⁡ (μ)) 2 {\ displaystyle \ dim _ {H} \ left \ {x: f '(x) = \ lim _ {h \ to 0 ^ {+}} {\ frac {\ mu ([x, x + h])} {h}} {\ text {не существует}} \ right \} = \ left (\ dim _ {H} \ operatorname { supp} (\ mu) \ right) ^ {2}}

\dim _{H}\left\{x:f'(x)=\lim _{h\to 0^{+}}{\frac {\mu ([x,x+h])}{h}}{\text{ does not exist}}\right\}=\left(\dim _{H}\operatorname {supp} (\mu)\right)^{2}

Позже Трошайт получил более полную картину множества, где производная не существует для более общих нормализованных мер Гибба, поддерживаемых самоконформными и самими -подобные наборы.

Функция вопросительного знака Германа Минковского визуально напоминает функцию Кантора, проявляясь как "сглаженная" форма последней; ее можно построить, перейдя от разложения непрерывной дроби к двоичному разложению, так же как функция Кантора может быть построена путем перехода от троичного разложения к двоичному разложению. Функция вопросительного знака имеет интересное свойство иметь нулевые производные при всех рациональных числах.

См. Также

Диадическое преобразование

Примечания

^Vestrup 2003, раздел 4.6.
^Thomson, Bruckner Bruckner 2008, стр. 252.
^http://mathworld.wolfram.com/CantorStaircaseFunction.html
^Басс 2013, стр. 28.
^Дарст, Ричард (1 сентября 1993 г.). «Размерность Хаусдорфа множества недифференцируемости функции Кантора равна [ln (2) / ln (3)] 2». Труды Американского математического общества. 119 (1): 105–108. doi : 10.2307 / 2159830. JSTOR 2159830.
^Фалконер, Кеннет Дж. (2004-01-01). «Односторонний мультифрактальный анализ и точки недифференцируемости чертовых лестниц». Математические труды Кембриджского философского общества. 136 (1): 167–174. Bibcode : 2004MPCPS.136..167F. doi : 10.1017 / S0305004103006960. ISSN 1469-8064.
^Трошайт, Саша (2014-03-01). «Гёльдеровская дифференцируемость самоконформных чертовых лестниц». Математические труды Кембриджского философского общества. 156 (2): 295–311. arXiv : 1301.1286. Bibcode : 2014MPCPS.156..295T. doi : 10.1017 / S0305004113000698. ISSN 1469-8064.

Ссылки

Басс, Ричард Франклин (2013) [2011]. Реальный анализ для аспирантов (Второе изд.). Createspace Independent Publishing. ISBN 978-1-4818-6914-0. CS1 maint: ref = harv (ссылка )
Кантор, Г. (1884). "De la puissance des ensembles parfaits de points: Extrait d'une lettre adressée à l'éditeur" [Сила идеальных наборов точек: отрывок из письма, адресованного редактору]. Acta Mathematica. International Press of Бостон. 4 : 381–392. doi : 10.1007 / bf02418423. ISSN 0001-5962.Перепечатано в : E. Zermelo (Ed.), Gesammelte Abhandlungen Mathematischen und Philosophischen Inhalts, Springer, New York, 1980.
Дарст, Ричард Б.; Палагалло, Джудит А.; Прайс, Томас Э. (2010), Любопытные кривые, Хакенсак, Нью-Джерси: World Scientific Publishing Co. Pte. Ltd., ISBN 978-981-4291-28-6, MR 2681574
Довгошей, О., Мартио, О..; Рязанов, В.; Вуоринен, М. (2006). «Функция Кантора» (PDF). Expositiones Mathematicae. Elsevier BV. 24 (1): 1–37. doi : 10.1016 / j.exmath.2005.05.002. ISSN 0723-0 869. MR 2195181.
Флерон, Джулиан Ф. (1994-04-01). «Заметка об истории множества Кантора и функции Кантора». Математический журнал. Informa UK Limited. 67 (2): 136–140. doi : 10.2307 / 2690689. ISSN 0025-570X. JSTOR 2690689.
Лебег, Х. (1904), Leçons sur l'intégration et la recherche des fonctions primitives [Уроки интеграции и поиска примитивных функций], Париж: Gauthier-Villars
Леони, Джованни (2017). Первый курс по соболевским просторам. 181 (2-е изд.). Провиденс, Род-Айленд: Американское математическое общество. п. 734. ISBN 978-1-4704-2921-8. OCLC 976406106.
Шеффер, Людвиг (1884). "Allgemeine Untersuchungen über Rectification der Curven" [Общие исследования по исправлению кривых]. Acta Mathematica. Международная пресса Бостона. 5 : 49–82. doi : 10.1007 / bf02421552. ISSN 0001-5962.
Thomson, Brian S.; Брукнер, Джудит Б.; Брукнер, Эндрю М. (2008) [2001]. Элементарный реальный анализ (Второе изд.). ClassicalRealAnalysis.com. ISBN 978-1-4348-4367-8. CS1 maint: ref = harv (ссылка )
Веструп, EM (2003). Теория меры и интеграция. Ряды Уайли в вероятности и статистике. John Wiley sons. ISBN 978-0471249771. CS1 maint: ref = harv (ссылка )
Витали, А. (1905), "Sulle funzioni integrali" [Об интегральных функциях], Атти, Академия наук, Турин, Кл. Наук, Физика, Матем. Природа, 40 : 1021–1034

Внешние ссылки

троичная функция Кантора в Энциклопедии математики
Функция Кантора Дугласа Риверса, Демонстрационный проект Вольфрама.
Вайстейн, Эрик У. «Функция Кантора». MathWorld.