Геометрическая прогрессия

редактировать

Диаграмма, показывающая три основные геометрические последовательности шаблона 1 (r) на глубину до 6 итераций. Первый блок представляет собой единичный блок, а пунктирная линия представляет бесконечную сумму последовательности, число, к которому она будет всегда приближаться, но никогда не касается: 2, 3/2 и 4/3 соответственно.

В математике геометрическая прогрессия, также известная как геометрическая последовательность, представляет собой последовательность из чисел где каждый член после первого находится путем умножения предыдущего на фиксированное, не единичное число, называемое обычным соотношением. Например, последовательность 2, 6, 18, 54,... представляет собой геометрическую прогрессию с обычным отношением 3. Аналогично, 10, 5, 2,5, 1,25,... - геометрическая последовательность с обычным отношением 1/2.

Примерами геометрической последовательности являются степени r фиксированного числа r, например 2 и 3. Общая форма геометрической последовательности -

a, ar, ar 2, ar 3, ar 4,… {\ displaystyle a, \ ar, \ ar ^ {2}, \ ar ^ {3}, \ ar ^ {4}, \ \ ldots}

a, \ ar, \ ar ^ {2}, \ ar ^ {3}, \ ar ^ {4}, \ \ ldots

где r ≠ 1 - это общее отношение, а a - масштабный коэффициент, равный начальному значению последовательности.

Содержание

1 Элементарные свойства
2 Геометрический ряд
- 2.1 Выведение
- 2.2 Связанные формулы
- 2.3 Бесконечный геометрический ряд
- 2.4 Комплексные числа
3 Продукт
- 3.1 Доказательство
4 История
5 См. Также
6 Ссылки
7 Внешние ссылки

Элементарные свойства

n-й член геометрической последовательности с начальным значением a = a 1 и обычное отношение r равно

an = arn - 1. {\ displaystyle a_ {n} = a \, r ^ {n-1}.}

a_ {n} = a \, r ^ {n -1}.

Такая геометрическая последовательность также следует рекурсивному отношению

an = ran - 1 {\ displaystyle a_ {n} = r \, a_ {n-1}}

a_ {n} = r \, a_ {n-1}

для каждого целого числа

n ≥ 1. {\ displaystyle n \ geq 1.}

n \ geq 1.

Как правило, чтобы проверить, является ли данная последовательность геометрической, просто проверяется, имеют ли все последовательные записи в последовательности одинаковое соотношение.

Общее отношение геометрической последовательности может быть отрицательным, что приводит к чередованию последовательности с чередованием чисел между положительными и отрицательными. Например,

1, -3, 9, -27, 81, -243,...

- это геометрическая последовательность с общим отношением -3.

Поведение геометрической последовательности зависит от значения общего отношения.. Если общее отношение:

положительно, все члены будут иметь тот же знак, что и исходный член.
отрицательный, члены будут чередоваться между положительным и отрицательным.
больше 1, будет экспоненциальный рост в сторону положительной или отрицательной бесконечности (в зависимости от знак начального члена).
1, прогрессия представляет собой постоянную последовательность.
между -1 и 1, но не нулем, будет экспоненциальное затухание к нулю (→ 0).
-1, абсолютное значение каждого члена в последовательности является постоянным, а члены меняют знак.
меньше -1, для абсолютные значения имеют экспоненциальный рост в сторону (без знака) бесконечности из-за чередования знаков.

Геометрические последовательности (с общим отношением, не равным -1, 1 или 0) демонстрируют экспоненциальный рост или экспоненциальное убывание, в отличие от линейного роста (или снижения) арифметическая прогрессия, например 4, 15, 26, 37, 48,… (с общей разницей 11). Этот результат получил Т.Р. Мальтус в качестве математической основы его принципа народонаселения. Обратите внимание, что два вида прогрессии связаны между собой: возведение в степень каждого члена арифметической прогрессии дает геометрическую прогрессию, а взятие логарифма каждого члена в геометрической прогрессии с положительным общим отношением дает арифметическую прогрессию.

Интересным результатом определения геометрической прогрессии является то, что любые три последовательных члена a, b и c будут удовлетворять следующему уравнению:

b 2 = ac {\ displaystyle b ^ {2} = ac }

b ^ {2} = ac

где b считается средним геометрическим между a и c.

Геометрический ряд

	2	+	10	+	50	+	250			=	312
- (			10	+	50	+	250	+	1250	=	5 × 312)

	2							−	1250	=	(1 - 5) × 312

Вычисление суммы 2 + 10 + 50 + 250. Последовательность последовательно умножается член на член на 5, а затем вычитается из исходной последовательности. Остаются два члена: первый член, а, и термин, следующий за последним, или ар. Желаемый результат, 312, находится путем вычитания этих двух членов и деления на 1-5.

A геометрический ряд - это сумма чисел в геометрической прогрессии. Например:

2 + 10 + 50 + 250 = 2 + 2 × 5 + 2 × 5 2 + 2 × 5 3. {\ displaystyle 2 + 10 + 50 + 250 = 2 + 2 \ times 5 + 2 \ times 5 ^ {2} +2 \ times 5 ^ {3}.}

{\ displaystyle 2 + 10 + 50 + 250 = 2 + 2 \ times 5 + 2 \ times 5 ^ {2} +2 \ times 5 ^ {3}.}

Пусть a будет первым членом (здесь 2), n - количество членов (здесь 4), а r - константа, на которую умножается каждый член, чтобы получить следующий член (здесь 5), сумма определяется как:

a (1 - rn) 1 - r {\ displaystyle {\ frac {a (1-r ^ {n})} {1-r}}}

{\ displaystyle {\ frac {a (1- r ^ {n})} {1-r}}}

В приведенном выше примере это дает:

2 + 10 + 50 + 250 = 2 ( 1 - 5 4) 1 - 5 = - 1248 - 4 = 312. {\ displaystyle 2 + 10 + 50 + 250 = {\ frac {2 (1-5 ^ {4})} {1-5}} = { \ frac {-1248} {- 4}} = 312.}

2 + 10 + 50 + 250 = {\ frac {2 (1-5 ^ {4})} {1-5 }} = {\ frac {-1248} {- 4}} = 312.

Формула работает для любых действительных чисел a и r (кроме r = 1, которое приводит к делению на ноль). Например:

- 2 π + 4 π 2-8 π 3 = - 2 π + (- 2 π) 2 + (- 2 π) 3 = - 2 π (1 - (- 2 π) 3) 1 - (- 2 π) = - 2 π (1 + 2 π 3) 1 + 2 π ≈ - 54,360768. {\ displaystyle -2 \ pi +4 \ pi ^ {2} -8 \ pi ^ {3} = - 2 \ pi + (- 2 \ pi) ^ {2} + (- 2 \ pi) ^ {3} = {\ frac {-2 \ pi (1 - (- 2 \ pi) ^ {3})} {1 - (- 2 \ pi)}} = {\ frac {-2 \ pi (1 + 2 \ pi ^ {3})} {1 + 2 \ pi}} \ приблизительно -54.360768.}

{\ displaystyle -2 \ pi +4 \ pi ^ {2} -8 \ pi ^ {3 } = - 2 \ pi + (- 2 \ pi) ^ {2} + (- 2 \ pi) ^ {3} = {\ frac {-2 \ pi (1 - (- 2 \ pi) ^ {3})} {1 - (- 2 \ pi)}} = {\ frac {-2 \ pi (1 + 2 \ pi ^ {3})} {1 + 2 \ pi}} \ приблизительно -54,360768.}

Поскольку вывод (ниже) не зависит от вещественности a и r, он также верен для комплексных чисел.

Вывод

Чтобы вывести эту формулу, сначала запишите общий геометрический ряд как:

∑ k = 1 nark - 1 = ar 0 + ar 1 + ar 2 + ar 3 + ⋯ + арн - 1. {\ displaystyle \ sum _ {k = 1} ^ {n} ar ^ {k-1} = ar ^ {0} + ar ^ {1} + ar ^ {2} + ar ^ {3} + \ cdots + ar ^ {n-1}.}

{\ displaystyle \ sum _ {k = 1} ^ {n} ar ^ {k-1} = ar ^ {0} + ar ^ {1} + ar ^ {2} + ar ^ {3} + \ cdots + ar ^ {n-1}.}

Мы можем найти более простую формулу для этой суммы, умножив обе части приведенного выше уравнения на 1 - r, и мы увидим, что

(1 - r) ∑ k = 1 нарк - 1 = (1 - r) (ar 0 + ar 1 + ar 2 + ar 3 + ⋯ + arn - 1) = ar 0 + ar 1 + ar 2 + ar 3 + ⋯ + arn - 1 - ar 1 - ar 2 - ar 3 - ⋯ - arn - 1 - arn = a - arn {\ displaystyle {\ begin {align} (1-r) \ sum _ {k = 1} ^ {n} ar ^ {k- 1} = (1-r) (ar ^ {0} + ar ^ {1} + ar ^ {2} + ar ^ {3} + \ cdots + ar ^ {n-1}) \\ = ar ^ {0} + ar ^ {1} + ar ^ {2} + ar ^ {3} + \ cdots + ar ^ {n-1} -ar ^ {1} -ar ^ {2} -ar ^ {3 } - \ cdots -ar ^ {n-1} -ar ^ {n} \\ = a-ar ^ {n} \ end {align}}}

{\ begin {align} (1-r) \ sum _ {k = 1} ^ {n} ar ^ {k-1} = (1-r) (ar ^ {0} + ar ^ {1} + ar ^ {2} + ar ^ {3} + \ cdots + ar ^ {n-1}) \\ = ar ^ {0} + ar ^ {1} + ar ^ {2} + ar ^ {3} + \ cdots + ar ^ {n-1} -ar ^ {1} -ar ^ {2} -ar ^ {3} - \ cdots -ar ^ {n-1} -ar ^ { n} \\ = a-ar ^ {n} \ end {align}}

, поскольку все остальные условия отменяются. Если r ≠ 1, мы можем изменить приведенное выше, чтобы получить удобную формулу для геометрического ряда, который вычисляет сумму n членов:

∑ k = 1 n a r k - 1 = a (1 - r n) 1 - r. {\ displaystyle \ sum _ {k = 1} ^ {n} ar ^ {k-1} = {\ frac {a (1-r ^ {n})} {1-r}}.}

\ sum _ {k = 1} ^ {n} ar ^ {k-1 } = {\ frac {a (1-r ^ {n})} {1-r}}.

Связанные формулы

Если бы суммирование началось не с k = 1, а с другого значения, например m, то

∑ k = mnark = a (rm - rn + 1) 1 - r, {\ displaystyle \ sum _ {k = m} ^ {n} ar ^ {k} = {\ frac {a (r ^ {m} -r ^ {n + 1})} {1-r}},}

{\ displaystyle \ sum _ {k = m} ^ {n} ar ^ {k} = {\ frac {a (r ^ {m} -r ^ {n + 1})} {1-r}},}

при условии $r ≠ 1 {\ displaystyle r \ neq 1}$ ${\ displaystyle r \ neq 1}$ . Если $r = 1 {\ displaystyle r = 1}$ $r = 1$ , тогда сумма равна только константе $a {\ displaystyle a}$ $a$ и поэтому равна $a (n - m + 1) {\ displaystyle a (n-m + 1)}$ ${\ displaystyle a (n-m + 1)}$ .

Дифференцирование этой формулы относительно r позволяет нам прийти к формулам для сумм вида

G s (n, r): = ∑ k = 0 nksrk. {\ displaystyle G_ {s} (n, r): = \ sum _ {k = 0} ^ {n} k ^ {s} r ^ {k}.}

{\ displaystyle G_ {s} (n, r): = \ sum _ {k = 0} ^ {n} k ^ {s} r ^ {k}.}

Например:

ddr ∑ k = 0 nrk = ∑ k = 1 nkrk - 1 = 1 - rn + 1 (1 - r) 2 - (n + 1) rn 1 - r. {\ displaystyle {\ frac {d} {dr}} \ sum _ {k = 0} ^ {n} r ^ {k} = \ sum _ {k = 1} ^ {n} kr ^ {k-1} = {\ frac {1-r ^ {n + 1}} {(1-r) ^ {2}}} - {\ frac {(n + 1) r ^ {n}} {1-r}}. }

{\ frac {d} {dr}} \ sum _ {k = 0} ^ {n} r ^ {k} = \ sum _ { k = 1} ^ {n} kr ^ {k-1} = {\ frac {1-r ^ {n + 1}} {(1-r) ^ {2}}} - {\ frac {(n + 1) r ^ {n}} {1-r}}.

Для геометрического ряда, содержащего только четные степени r, умножаем его на 1 - r:

(1 - r 2) ∑ k = 0 nar 2 k = a - ar 2 n + 2. {\ displaystyle (1-r ^ {2}) \ sum _ {k = 0} ^ {n} ar ^ {2k} = a-ar ^ {2n + 2}.}

(1- r ^ {2}) \ sum _ {k = 0} ^ {n} ar ^ {2k} = a-ar ^ {2n + 2}.

Тогда

∑ k = 0 нар 2 К = а (1 - г 2 п + 2) 1 - г 2. {\ displaystyle \ sum _ {k = 0} ^ {n} ar ^ {2k} = {\ frac {a (1-r ^ {2n + 2})} {1-r ^ {2}}}.}

\ sum _ {k = 0} ^ {n} ar ^ {2k} = {\ frac {a (1-r ^ {2n + 2})} {1-r ^ {2}}}.

Аналогично, возьмите r как обычное отношение и используйте стандартную формулировку.

Для ряда только с нечетными степенями r

(1 - r 2) ∑ k = 0 nar 2 k + 1 = ar - ar 2 n + 3 {\ displaystyle (1-r ^ { 2}) \ sum _ {k = 0} ^ {n} ar ^ {2k + 1} = ar-ar ^ {2n + 3}}

(1-r ^ {2}) \ sum _ {k = 0} ^ {n} ar ^ {2k + 1} = ar-ar ^ {2n + 3}

∑ k = 0 nar 2 k + 1 = ар (1 - г 2 п + 2) 1 - г 2. {\ displaystyle \ sum _ {k = 0} ^ {n} ar ^ {2k + 1} = {\ frac {ar (1-r ^ {2n + 2})} {1-r ^ {2}}}.}

\ sum _ {k = 0} ^ {n} ar ^ {2k +1} = {\ frac {ar (1-r ^ {2n + 2})} {1-r ^ {2}}}.

Точная формула для обобщенной суммы $G s (n, r) {\ displaystyle G_ {s} (n, r)}$ ${\ displaystyle G_ {s} (n, r)}$ когда $s ∈ N {\ displaystyle s \ in \ mathbb {N}}$ ${\ displaystyle s \ in \ mathbb {N}}$ расширяется на числа Стирлинга второго рода как

G s (n, r) = ∑ j = 0 s { sj} xjdjdxj [1 - xn + 1 1 - x]. {\ displaystyle G_ {s} (n, r) = \ sum _ {j = 0} ^ {s} \ left \ lbrace {s \ atop j} \ right \ rbrace x ^ {j} {\ frac {d ^ {j}} {dx ^ {j}}} \ left [{\ frac {1-x ^ {n + 1}} {1-x}} \ right].}

{\ displaystyle G_ {s} (n, r) = \ sum _ {j = 0} ^ {s} \ left \ lbrace {s \ atop j} \ right \ rbrace x ^ {j } {\ frac {d ^ {j}} {dx ^ {j}}} \ left [{\ frac {1-x ^ {n + 1}} {1-x}} \ right].}

Бесконечный геометрический ряд

бесконечный геометрический ряд - это бесконечный ряд, последовательные члены которого имеют общее отношение. Такой ряд сходится тогда и только тогда, когда абсолютное значение общего отношения меньше единицы (| r | < 1). Its value can then be computed from the finite sum formula

∑ k = 0 ∞ ark = lim n → ∞ ∑ к знак равно 0 nark = lim n → ∞ a (1 - rn + 1) 1 - r = a 1 - r - lim n → ∞ arn + 1 1 - r {\ displaystyle \ sum _ {k = 0} ^ {\ infty} ar ^ {k} = \ lim _ {n \ to \ infty} {\ sum _ {k = 0} ^ {n} ar ^ {k}} = \ lim _ {n \ to \ infty} {\ гидроразрыв {a (1-r ^ {n + 1})} {1-r}} = {\ frac {a} {1-r}} - \ lim _ {n \ to \ infty} {\ frac {ar ^ {n + 1}} {1-r}}}

\ sum _ {k = 0} ^ {\ infty} ar ^ {k} = \ lim _ {n \ to \ infty} {\ sum _ {k = 0} ^ {n} ar ^ {k}} = \ lim _ {n \ to \ infty} {\ frac {a (1-r ^ {n + 1})} {1-r}} = {\ frac {a} {1-r}} - \ lim _ {n \ to \ infty} {\ frac {ar ^ {n + 1}} {1-r}}

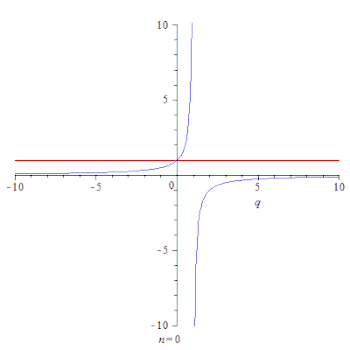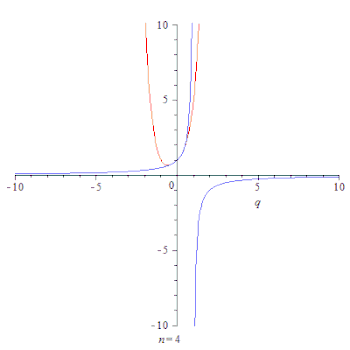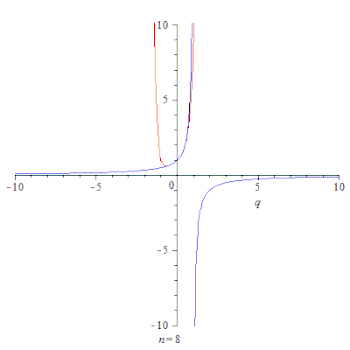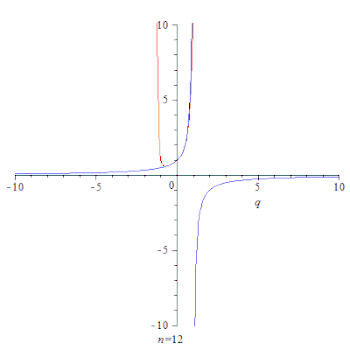
Анимация, показывающая сходимость частичных сумм геометрической прогрессии

∑ k = 0 nqk {\ displaystyle \ sum \ limits _ {k = 0} ^ { n} q ^ {k}}

{\ displaystyle \ sum \ limits _ {k = 0} ^ {n} q ^ {k}}

(красная линия) до его суммы

1 1 - q {\ displaystyle {1 \ over 1-q}}

{\ displaystyle { 1 \ over 1-q}}

(синяя линия) for

| q | < 1 {\displaystyle |q|<1}

| q | <1

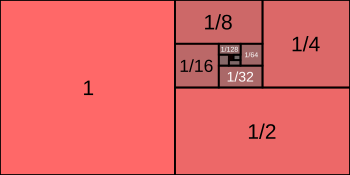
Диаграмма, показывающая геометрический ряд 1 + 1/2 + 1/4 + 1/8 + ⋯, который сходится к 2.

Поскольку:

rn + 1 → 0 при n → ∞, когда | r | < 1. {\displaystyle r^{n+1}\to 0{\t_dv{ as }}n\to \infty {\t_dv{ when }}|r|<1.}

r ^ {n + 1} \ to 0 {\ t_dv {as}} n \ to \ infty { \ t_dv {when}} | r | <1.

Тогда:

∑ k = 0 ∞ ark = a 1 - r - 0 = a 1 - r {\ displaystyle \ sum _ {k = 0} ^ {\ infty} ar ^ {k} = {\ frac {a} {1-r}} - 0 = {\ frac {a} {1-r}}}

\ sum _ {k = 0} ^ {\ infty} ar ^ {k} = {\ frac {a} {1-r }} - 0 = {\ frac {a} {1-r}}

Для серии, содержащей только четные мощности ers из $р {\ displaystyle r}$ $r$ ,

∑ k = 0 ∞ ar 2 k = a 1 - r 2 {\ displaystyle \ sum _ {k = 0} ^ {\ infty} ar ^ {2k} = {\ frac {a} {1-r ^ {2}}}}

\ sum _ {k = 0} ^ {\ infty} ar ^ {2k} = {\ frac {a} {1-r ^ {2}}}

и только для нечетных степеней

∑ k = 0 ∞ ar 2 k + 1 = ar 1 - r 2 {\ displaystyle \ sum _ {k = 0} ^ {\ infty} ar ^ {2k + 1} = {\ frac {ar} {1-r ^ {2}}}}

\ sum _ {k = 0} ^ {\ infty} ar ^ {2k + 1} = {\ frac {ar} {1-r ^ {2 }}}

В случаях, когда сумма не начинается с k = 0,

∑ К знак равно м ∞ ark = рука 1 - r {\ displaystyle \ sum _ {k = m} ^ {\ infty} ar ^ {k} = {\ frac {ar ^ {m}} {1 -r}}}

\ sum _ {k = m} ^ {\ infty} ar ^ {k} = {\ frac {ar ^ {m}} {1-r}}

Приведенные выше формулы действительны только для | r | < 1. The latter formula is valid in every Банахова алгебра, если норма r меньше единицы, а также в поле p-адических чисел, если | r | p< 1. As in the case for a finite sum, we can differentiate to calculate formulae for related sums. For example,

ddr ∑ k = 0 ∞ rk знак равно ∑ К знак равно 1 ∞ krk - 1 знак равно 1 (1 - r) 2 {\ displaystyle {\ frac {d} {dr}} \ sum _ {k = 0} ^ {\ infty} r ^ {k} = \ sum _ {k = 1} ^ {\ infty} kr ^ {k-1} = {\ frac {1} {(1-r) ^ {2}}}}

{\ displaystyle {\ frac {d} {dr} } \ sum _ {k = 0} ^ {\ infty} r ^ {k} = \ sum _ {k = 1} ^ {\ infty} kr ^ {k-1} = {\ frac {1} {(1 -r) ^ {2}}}}

Эта формула работает только для | r | < 1 as well. From this, it follows that, for |r| < 1,

∑ k = 0 ∞ k r k = r (1 - r) 2; ∑ К знак равно 0 ∞ К 2 р К знак равно г (1 + г) (1 - г) 3; ∑ К знак равно 0 ∞ К 3 рк знак равно р (1 + 4 р + р 2) (1 - г) 4 {\ displaystyle \ sum _ {k = 0} ^ {\ infty} kr ^ {k} = {\ frac {r} {\ left (1-r \ right) ^ {2}}} \,; \, \ sum _ {k = 0} ^ {\ infty} k ^ {2} r ^ {k} = {\ frac {r \ left (1 + r \ right)} {\ left (1-r \ right) ^ {3}}} \,; \, \ sum _ {k = 0} ^ {\ infty} k ^ { 3} r ^ {k} = {\ frac {r \ left (1 + 4r + r ^ {2} \ right)} {\ left (1-r \ right) ^ {4}}}}

\ sum _ {k = 0} ^ {\ infty} kr ^ {k} = {\ frac {r} {\ left (1-r \ right) ^ {2}}} \,; \, \ sum _ {k = 0} ^ {\ infty} k ^ {2} r ^ {k} = {\ frac {r \ left (1 + r \ right) } {\ left (1-r \ right) ^ {3}}} \,; \, \ sum _ {k = 0} ^ {\ infty} k ^ {3} r ^ {k} = {\ frac { r \ left (1 + 4r + r ^ {2} \ right)} {\ left (1-r \ right) ^ {4}}}

Также, бесконечный ряд 1/2 + 1/4 + 1/8 + 1/16 + ⋯ является элементарным примером ряда, который абсолютно сходится.

Это геометрический ряд, первый член которого равен 1/2, а общее отношение равно 1/2, поэтому его сумма равна

1 2 + 1 4 + 1 8 + 1 16 + ⋯ = 1/2 1 - (+ 1 / 2) = 1. {\ displaystyle {\ frac {1} {2}} + {\ frac {1} {4}} + {\ frac {1} {8}} + {\ frac {1} {16} } + \ cdots = {\ frac {1/2} {1 - (+ 1/2)}} = 1.}

{\ frac {1} {2} } + {\ frac {1} {4}} + {\ frac {1} {8}} + {\ frac {1} {16}} + \ cdots = {\ frac {1/2} {1- ( +1/2)}} = 1.

Обратное к вышеуказанному ряду: 1/2 - 1/4 + 1 / 8 - 1/16 + ⋯ - простой пример чередующегося ряда, который абсолютно сходится.

Это геометрический ряд, первый член которого равен 1/2, а общее отношение равно -1/2, поэтому его сумма равна

1 2 - 1 4 + 1 8 - 1 16 + ⋯ = 1/2 1 - (- 1/2) = 1 3. {\ displaystyle {\ frac {1} {2}} - {\ frac {1} {4}} + {\ frac {1} {8}} - {\ frac {1} {16}} + \ cdots = {\ frac {1/2} {1 - (- 1/2)}} = {\ frac {1} {3}}.}

{\ frac {1} {2}} - {\ frac {1) } {4}} + {\ frac {1} {8}} - {\ frac {1} {16}} + \ cdots = {\ frac {1/2} {1 - (- 1/2)}} = {\ frac {1} {3}}.

Комплексные числа

Формула суммирования для геометрических рядов остается действительно, даже если обычное отношение - комплексное число. В этом случае условие, что абсолютное значение r меньше 1, превращается в то, что модуль r будет меньше 1. Можно вычислить суммы некоторых неочевидных геометрических рядов. Например, рассмотрим предложение

∑ k = 0 ∞ sin ⁡ (kx) rk = r sin ⁡ (x) 1 + r 2 - 2 r cos ⁡ (x) {\ displaystyle \ sum _ {k = 0} ^ {\ infty} {\ frac {\ sin (kx)} {r ^ {k}}} = {\ frac {r \ sin (x)} {1 + r ^ {2} -2r \ cos (x) }}}

\ sum _ {k = 0} ^ {\ infty} {\ frac {\ sin (kx)} {r ^ {k}}} = {\ frac {r \ sin (x)} {1 + r ^ {2} -2r \ cos (x)}}

Доказательством этого служит тот факт, что

sin ⁡ (kx) = eikx - e - ikx 2 i, {\ displaystyle \ sin (kx) = {\ frac {e ^ {ikx} -e ^ {- ikx}} {2i}},}

\ sin (kx) = {\ frac {e ^ {ikx} -e ^ {- ikx}} {2i}},

, которое является следствием формулы Эйлера. Подстановка этого в исходный ряд дает

∑ k = 0 ∞ sin ⁡ (kx) rk = 1 2 i [∑ k = 0 ∞ (eixr) k - ∑ k = 0 ∞ (e - ixr) k] {\ displaystyle \ sum _ {k = 0} ^ {\ infty} {\ frac {\ sin (kx)} {r ^ {k}}} = {\ frac {1} {2i}} \ left [\ sum _ { k = 0} ^ {\ infty} \ left ({\ frac {e ^ {ix}} {r}} \ right) ^ {k} - \ sum _ {k = 0} ^ {\ infty} \ left ( {\ frac {e ^ {- ix}} {r}} \ right) ^ {k} \ right]}

\ sum _ {k = 0} ^ {\ infty} {\ frac {\ sin (kx)} {r ^ {k}}} = {\ frac {1} {2i}} \ left [\ sum _ {k = 0} ^ {\ infty} \ left ({\ frac {e ^ {ix}} {r}} \ right) ^ {k} - \ sum _ {k = 0} ^ {\ infty} \ left ({\ frac { e ^ {- ix}} {r}} \ right) ^ {k} \ right]

В этом разница двух геометрических рядов, и поэтому это простое применение формулы для бесконечного геометрическая серия, завершающая доказательство.

Продукт

Произведение геометрической прогрессии - это произведение всех терминов. Его можно быстро вычислить, взяв среднее геометрическое первого и последнего отдельных членов прогрессии и возведя это среднее в степень, определяемую количеством членов. (Это очень похоже на формулу для суммы членов арифметической последовательности : возьмите среднее арифметическое первого и последнего отдельных членов и умножьте на количество членов.)

Поскольку среднее геометрическое двух чисел равно квадратному корню из их произведения, произведение геометрической прогрессии составляет:

∏ i = 0 nari = (a ⋅ arn) n + 1 = (a 2 rn) N + 1 {\ Displaystyle \ prod _ {я = 0} ^ {n} ar ^ {i} = ({\ sqrt {a \ cdot ar ^ {n}}}) ^ {n + 1} = ({\ sqrt {a ^ {2} r ^ {n}}}) ^ {n + 1}}

{\ displaystyle \ prod _ {i = 0} ^ {n} ar ^ {i} = ({\ sqrt {a \ cdot ar ^ {n}}}) ^ {n + 1} = ({\ sqrt { a ^ {2} r ^ {n}}}) ^ {n + 1}}

(Интересный аспект этой формулы заключается в том, что, даже если она включает извлечение квадратного корня из потенциально- нечетная степень потенциально отрицательного r, он не может дать сложный результат, если ни a, ни r не имеют мнимой части. Возможно, если r будет отрицательным, а n нечетным, для извлечения квадратного корня из отрицательного промежуточного результата, в результате чего последующий промежуточный результат будет мнимым числом. Однако образованный таким образом воображаемый промежуточный результат вскоре будет ra вычисляется в степени $n + 1 {\ displaystyle \ textstyle n + 1}$ ${\ displaystyle \ textstyle n + 1}$ , которое должно быть четным числом, потому что n само по себе было нечетным; таким образом, окончательный результат вычисления может быть вероятным нечетным числом, но никогда не может быть мнимым.)

Доказательство

Пусть P представляет продукт. По определению, его вычисляют путем явного умножения каждого отдельного члена вместе. Записано полностью,

P = a ⋅ ar ⋅ ar 2 ⋯ arn - 1 ⋅ arn {\ displaystyle P = a \ cdot ar \ cdot ar ^ {2} \ cdots ar ^ {n-1} \ cdot ar ^ {n}}

{\ displaystyle P = a \ cdot ar \ cdot ar ^ {2} \ cdots ar ^ {n-1} \ cdot ar ^ { n}}

Выполняя умножение и собирая подобные члены,

P = an + 1 r 1 + 2 + 3 + ⋯ + (n - 1) + n {\ displaystyle P = a ^ {n +1} r ^ {1 + 2 + 3 + \ cdots + (n-1) + n}}

{\ displaystyle P = a ^ {n + 1} r ^ {1 + 2 + 3 + \ cdots + (n-1) + n}}

Показателем степени r является сумма арифметической последовательности. Подставляя формулу для этого расчета,

P = an + 1 rn (n + 1) 2 {\ displaystyle P = a ^ {n + 1} r ^ {\ frac {n (n + 1)} {2} }}

{\ displaystyle P = a ^ {n + 1} r ^ {\ frac {n (n + 1)} {2}}}

, который позволяет упростить выражение до

P = (arn 2) n + 1 = (arn) n + 1 {\ displaystyle P = (ar ^ {\ frac {n} {2}}) ^ {n + 1} = (a {\ sqrt {r ^ {n}}}) ^ {n + 1}}

{\ displaystyle P = (ar ^ {\ frac {n} {2}}) ^ {n + 1} = (a {\ sqrt { r ^ {n}}}) ^ {n + 1}}

Переписываем a как $a 2 {\ displaystyle \ textstyle {\ sqrt {a ^ { 2}}}}$ ${\ displaystyle \ textstyle {\ sqrt {a ^ {2}}}}$ ,

P = (a 2 rn) n + 1 {\ displaystyle P = ({\ sqrt {a ^ {2} r ^ {n}}}) ^ {n + 1}}

{\ displaystyle P = ({\ sqrt {a ^ {2} r ^ {n}}}) ^ {n + 1}}

что завершает доказательство.

История

Глиняная табличка раннего династического периода в Месопотамии, MS 3047, содержит геометрическую прогрессию с основанием 3 и множителем 1/2. Предполагается, что это шумер, из города Шуруппак. Это единственное известное свидетельство геометрической прогрессии до вавилонской математики.

Книги VIII и IX Евклида Элементы, анализирующие геометрические прогрессии (например, степени двойки, подробности см. в статье) и приведите несколько их свойств.

См. также

Арифметическая прогрессия - последовательность чисел с постоянной разницей между последовательными числами
Арифметико-геометрическая последовательность
Линейное разностное уравнение
Экспоненциальная функция - класс математических функций
Гармоническая прогрессия
Гармоническая последовательность - Бесконечная последовательность обратных положительных целых чисел
Бесконечный ряд - Бесконечная сумма
Предпочтительное число - Стандартные рекомендации по выбору точных размеров продукта в рамках заданного набора ограничений
Томас Роберт Мальтус - британский политический экономист
Геометрический распределение

Ссылки

Холл и Найт, Высшая алгебра, с. 39, ISBN 81-8116-000-2

Внешние ссылки