Войти
Рис. 1: Обзор типов абстрактных пространств. Стрелка указывает, что это тоже своего рода; например, нормированное пространство также является метрическим пространством. В математике пространство представляет собой набор (иногда называемый вселенной ) с некоторой добавленной структурой .
В то время как современная математика использует много типов пространств, таких как евклидовы пространства, линейные пространства, топологические пространства, Гильбертовы или вероятностные пространства, он не понятие «пространство» как таковое.
Пространство состоит из выбранных математических объектов, рассматриваются как точки и выбранные отношения между этими точками. Природа точек может широко распространяться: например, точки могут быть включены в набор других пространств. Именно отношения определяют природу пространства. Точнее, изоморфные пространства признанными, где изоморфизм между двумя пространствами - это взаимно однозначное соответствие между их точками, которое сохраняет. Например, отношения между точками трехмерного евклидова пространства однозначно определяются аксиомами Евклида, и все трехмерные евклидовы пространства идентичными.
Топологические понятия, такие как непрерывность, имеют естественные определения в каждом евклидовом пространстве. Однако топология не отличает прямые линии от кривых, и связь между евклидовым и топологическим пространством, таким образом, «забывает». Аналогичные отношения более подробно рассматриваются в разделе «Типы пространств».
Не всегда ясно, следует ли рассматривать данный математический объект как геометрическое «пространство» или как алгебраическую «структуру». Общее определение «структуры», предложенное Бурбаки, охватывает все распространенные типы пространств, дает общее определение изоморфизма и оправдывает перенос свойств между изоморфными структурами.
| Классика | Современные |
|---|---|
| аксиомы - очевидные следствия определений | аксиомы - обычные |
| теоремы - абсолютная объективная истина | теоремы - последствия соответственно аксиом |
| отношения между точками, линиями и т. д. определяет их природой | отношения между точками, линиями и т. д. важны; их природа не |
| даны нам математические объекты с их структурой | каждая математическая теория некоторые объекты из их свойств |
| геометрия соответствует экспериментальной реальности | геометрия математическая истина |
| все геометрические свойства пространства следуют из аксиом | аксиомы пространства не обязательно определяют все геометрические свойства |
| геометрия - это автономная и живая наука | классическая геометрия это универсальный язык математики |
| пространство трехмерно | разные концепции измерения применяются к разным видам пространств |
| пространство - это вселенная геометрия | пространства - это просто математические структуры, они встречаются в различных областях математики |
Рис. 2: Гомотетия преобразует геометрическую фигуру в аналогичную масштабирования. В древнегреческой математике «пространство» было геометрической абстракцией трехмерной реальности, наблюдаемой в повседневной жизни. Около 300 г. до н.э. Евклид дал аксиомы для свойств пространства. Евклид построил всю математику на этих геометрических основ, так далеко, чтобы определить число путем сравнения длин отрезков к длине выбранного опорного сегмента.
Метод координат (аналитическая геометрия ) был принят Рене Декартом в 1637 году. В то время геометрические теоремы рассматривались как абсолютные объективные истины, познаваемые через интуицию и разум, аналогичный объектм естествознания; и аксиомы рассматривались как очевидные следствия определений.
Были использованы два отношения эквивалентности между геометрическими фигурами: конгруэнтность и подобие. Переводы, вращения и отражения превращают фигуру в конгруэнтные фигуры; гомотетии - в аналогичные цифры. Например, все похожи круги друг на друга, но эллипсы не похожи на круги. Третье отношение эквивалентности, введенное Гаспаром Монжем в 1795 году, встречается в проективной геометрии : не только эллипсы, но также параболы и гиперболы превращаются в круги при соответствующих проективных преобразованиях; все они являются проективно эквивалентными фигурами.
Связь между двумя геометриями, евклидовой и проективной, показывает, что математические объекты не даны нам с их структурой. Скорее, каждая математическая теория использует свои объекты с помощью некоторых из их свойств, а именно те, которые положены в качестве аксиом в основе теории.
Расстояния и углы не могут фигурировать в теоремахективной геометрии, поскольку эти понятия не являются ни тем, ни другим. упомянутые в аксиомах проективной геометрии и упомянутых там понятий. Вопрос «какова сумма трех углов треугольника» имеет смысл в евклидовой геометрии, но не имеет смысла в проективной геометрии.
Иная ситуация в возникла в 19 веке: в некоторой геометрии сумма трех углов треугольника четко определена, но отличается от классического значения (180 градусов). Неевклидова гиперболическая геометрия, введенная Николаем Лобачевским в 1829 году и <289 Яношом Бойяи в 1832 году (и Карлом Фридрихом Гауссом в 1816 году, не опубликовано) заявлено, что сумма зависит от треугольника и всегда меньше 180 градусов. Эухенио Бельтрами в 1868 году и Феликс Клейн в 1871 году получили евклидовы «модели» неевклидовой гиперболической геометрии и тем полностью подтвердили эту теорию как логическую возможность.
Это открытие заставило отказаться от претензий на абсолютную истину евклидовой геометрии. Он показал, что аксиомы не являются «очевидными» и не «следствиями определенных». Скорее, это гипотезы. Насколько они соответствуют экспериментальной реальности? Эта важная физическая проблема больше не имеет ничего общего с математикой. Даже если «геометрия» не соответствует экспериментальной реальности, ее теоремы остаются менее «математическими истинами».
Евклидова модель неевклидовой геометрии - это выбор некоторых объектов, необходимых в евклидовом пространстве, и некоторые отношения между объектами, которые удовлетворяют всем аксиомам (и, следовательно, всем теоремам) неевклидовой геометрии. Эти евклидовы объекты и отношения «играют» неевклидову геометрию, как современные актеры разыгрывают античный спектакль. Актеры могут имитировать ситуацию, которой никогда не было в реальности. Отношения между актерами на сцене имитируют отношения между персонажами спектакля. Точно так же выбранные отношения между выбранными объектами евклидовой модели имитируют неевклидовы отношения. Это показывает, что отношения между объектами важны в математике, в то время как природа объектов - нет.
Слово «геометрия» (от древнегреческого: гео- «земля», -метрон «измерение») использование означало практический способ обработки длин, регионов и объемы в пространстве, в котором мы живем, но затем широко распространился (как и понятие, о котором здесь идет речь).
Согласно Бурбаки, период между 1795 г. (Géométrie, описывающий Монжа) и 1872 г. («Эрлангенская программа» Кляйна) можно назвать золотым веком геометрии. Первоначальное пространство, исследованное Евклидом, теперь называется трехмерным евклидовым пространством. Его аксиоматизация, начатая Евклидом 23 века назад, была реформирована с помощью аксиом Гильберта, аксиом Тарского и аксиом Биркгофа. Эти системы аксиом описывают пространство с помощью примитивных понятий (таких как «точка», «между», «конгруэнтность»), ограниченных рядом аксиом .
Аналитическая геометрия достигла больших успехов и преуспела в замене теоремы классической геометрии вычислениями через инварианты групп преобразований. С того времени новые теоремы классической геометрии стали интересовать больше любителей, чем профессиональных математиков. Однако наследие классической геометрии не было потеряно. По словам Бурбаки, «классическая геометрия, оставленная в роли автономной и живой, превращается, таким образом, в универсальный язык современной математики».
Одновременно числа начали вытеснять геометрию как основу математики. Например, в эссе Ричарда Дедекинда 1872 года Stetigkeit und irrationale Zahlen (Непрерывность и иррациональные числа) он утверждает, что точки на линии должны обладать свойствами разрезов Дедекинда, и поэтому линия была самой тем же. как набор действительных чисел. Дедекинд осторожно отмечает, что это предположение невозможно доказать. В трактовках утверждение Дедекинда часто рассматривается как определение линии, тем самым сводя геометрию к арифметике. Трехмерное евклидово пространство определяется как аффинное пространство, связанное с ним пространство разностей его элементов снабжено внутренним продуктом. Определение «с нуля», как оно сейчас используется в Евклида, не раскрывает отношения этого пространства к другим пространствам. Кроме того, трехмерное проективное пространство теперь определяется как пространство всех одномерных подпространств (то есть прямых линий, проходящих через начало координат) четырехмерного пространства пространства. Этот сдвиг в основах требует нового набора аксиом, и если эти аксиомы будут приняты, классические аксиомы геометрии станут теоремами.
Пространство теперь состоит из выбранных математических объектов (например, функций в другом пространстве, или просто элементов набора), рассматриваемых как точек, и выбранных отношений между этими точками. Следовательно, пробелы - это просто удобные математические конструкции. Можно ожидать, что структуры, называемые «пространствами», воспринимаются более геометрически, чем другие математические объекты, но это не всегда верно.
Согласно знаменитой вступительной лекции, прочитанной Бернхардом Риманом в 1854 году, каждый математический объект, параметризованный действительными числами, можно рассматривать как точку n-мерного пространства всех таких объектов. Современные математики регулярно следуют этой идее и находят привлекательное использование терминологии классической геометрии почти везде.
Функции - важные математические объекты. Обычно они образуют бесконечномерные функциональные пространства, как уже отмечал Риман и разработал в 20-м веке с помощью функционального.
Хотя каждый тип пространства имеет собственное определение, общая идея «пространства» ускользает от формы использования. Некоторые структуры называются пространствами, другие - нет, без формального критерия. Более того, нет единого мнения по поводу общей идеи «структуры». По словам Пудлака, «математику [...] нельзя полностью объяснить с помощью одного понятия, такого как математическая структура. Тем не менее, структуралистский подход Бурбаки - лучшее, что у нас есть ». Мы вернемся к структурелистскому подходу в последнем разделе «Пространства и структуры», а теперь обрисовываем возможную класси настройки пространств (и структур) в духе Бурбаки.
Мы классифицируем пространства на трех уровнях. Учитывая, что каждая математическая теория использует свои объекты с помощью некоторых из их свойств, первый вопрос, который следует указать: какие свойства? Это приводит к первому (верхнему) классификацию. На втором уровне учитываются ответы на особо важные вопросы (среди вопросов, имеющих смысл согласно первому уровню). На третьем уровне учитываются все возможные вопросы.
Например, классификация верхнего уровня различает евклидовы и проективные пространства, поскольку расстояние между двумя точками определено в евклидовых пространствах, но не определено в проективных пространствах. Другой пример. Вопрос «какова сумма трех углов треугольника» смысл в евклидовом пространственном изображении, но не в проективном пространстве. В неевклидовом вопросе имеет смысл, но на него ответят по-другому, что не является различием верхнего уровня.
Кроме того различием между евклидовой плоскостью и евклидовым трехмерным пространством не является различием верхнего уровня; вопрос «каков размер» имеет смысл в обоих случаях.
Классификация второго уровня различает, например, евклидовы и неевклидовы пространства; между конечным и бесконечномерным пространством; между компактными и некомпактными пространствами и т. д. В терминах Бурбаки классификация второго уровня - это классификация по «видум». В отличие от биологической таксономии пространство может принадлежать нескольким видам.
Классификация третьего уровня различает, например, пространство разной размерности, но не различает плоскость трехмерного евклидова пространства, рассматриваемого как двумерное евклидово пространство, и набор всех пар действующих чисел, также рассматриваемые как двумерное евклидово пространство. Точно так же он не делает различий между разными евклидовыми моделями одного и того же неевклидова пространства. Более формально, третий уровень классифицирует пространство до изоморфизма. Изоморфизм между двумя пространствами определен как взаимно однозначное соответствие между точками первого и точками второго пространства, которое обеспечивает все отношения, оговоренные в соответствии с первым уровнем. Взаимно изоморфные пространства копиями одного пространства. Один из них принадлежит к данному виду, то они все принадлежат.
Понятие изоморфизма проливает свет на классификацию верхнего уровня. Учитывая взаимно однозначное соответствие между двумя пространствами одного и того же верхнего уровня, можно спросить, является ли это изоморфизмом или нет. Этот вопросне имеет смысла для двух пространств разных классов.
Изоморфизм самому себе называется автоморфизмом. Автоморфизмы евклидова пространства - это сдвиги, повороты, отражения и их композиции. Евклидово пространство однородно в том смысле, что каждая точка может быть преобразована в любую другую точку с помощью некоторого автоморфизма.
Евклидовы аксиомы не оставляют свободы; они однозначно определяют все геометрические свойства пространства. Точнее: все трехмерные евклидовы пространства взаимно изоморфны. В этом смысле мы имеем «трехмерное евклидово пространство». По мнению Бурбаки, соответствующая теория однозначна. Напротив, топологические пространства обычно неизоморфны; их теория многовалентна. Аналогичная идея мощности в математической логике: теория называется категоричной, если все ее модели одной изоморфны другу. Согласно Бурбаки, изучение многовалентных теорий является наиболее яркой чертой, которая отличает современную математику от классической математики.
Топологические понятия (непрерывность, сходимость, открытые числа, замкнутые числа и т. Д.) Естественным образом управление в каждом евклидовом пространстве. Другими словами, каждое евклидово пространство также является топологическим пространством. Каждый изоморфизм между двумя евклидовыми пространствами также является изоморфизмом между топологическими пространствами (так называемый «гомеоморфизм »), но обратное неверно: гомеоморфизм может искажать расстояния. В терминах Бурбаки «топологическое пространство» является основным структурой «евклидово пространство». Подобные идеи встречаются в теории категорий : категория евклидовых пространств - это конкретная категория над категорией топологических пространств; функтор забывчивый (или "снимающий") отображает первую категорию во вторую категорию.
Трехмерное евклидово пространство - это частный случай евклидова пространства. С точки зрения Бурбаки, виды трехмерного евклидова пространства богаче видов евклидова пространства. Точно так же виды компактного топологического пространства богаче видов топологического пространства.
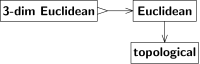Рис. 3: Пример отношений между видами пространств Такие отношения между видами пространств можно выразить схематически, как показано на рис. 3. Стрелка от A к B означает, что каждое A-пространство также является B-пространством или может быть рассматривается как B-пространство, или предоставляет B-пространство и т.д. Рассматривая A и B как классы пространств, можно интерпретировать стрелку как переход от A к B. (в терминах Бурбаки, «процедура вывода» B -пространство из A-пространства. Не совсем функция, если только классы A, B не являются наборами; этот нюанс не отменяет следующего.) Две стрелки на рис. 3 не обратимы, но для разных причины.
Переход от «евклидова» к «топологическому» забывчив. Топология отличает непрерывную от прерывистой, но не отличает прямолинейную от криволинейной. Интуиция подсказывает нам, что евклидова структура не может быть восстановлена по топологии. Доказательство использует автоморфизм топологического пространства (то есть самогомеоморфизм ), который не является автоморфизмом евклидова пространства (то есть не является композицией сдвигов, вращений и отражений). Такое преобразование превращает данную евклидову структуру в (изоморфную, но) другую евклидову структуру; обе евклидовы структуры соответствуют единой топологической структуре.
Напротив, переход от «трехмерного евклидова» к «евклидову» не забывает; Евклидово пространство не обязательно должно быть трехмерным, но если оно оказывается трехмерным, оно является полноценным, структура не теряется. Другими словами, последний переход является инъективным (один-к-одному), тогда как первый переход не является инъективным (многие-к-одному). Обозначим инъективные переходы стрелкой с зазубренным хвостом, «↣», а не «→».
Оба перехода не являются сюръективными, то есть не каждое B-пространство является результатом некоторого A-пространства. Во-первых, трехмерное евклидово пространство - это частный (не общий) случай евклидова пространства. Во-вторых, топология евклидова пространства - это частный случай топологии (например, оно должно быть некомпактным, связным и т. Д.). Мы обозначаем сюръективные переходы двуглавой стрелкой, а не «→». См., Например, Рис. 4; там стрелка от «реальной линейной топологии» к «действительной линейной» является двуглавой, поскольку каждое реальное линейное пространство допускает некоторую (по крайней мере одну) топологию, совместимую с его линейной структурой.
Такая топология в общем случае не уникальна, но уникальна, когда реальное линейное пространство конечномерно. Для этих пространств переход является одновременно инъективным и сюръективным, то есть биективным ; см. стрелку от «конечно-тусклой реальной линейной топологии» к «конечно-тусклой реальной линейной»интегрирования определяет интегрируемость и интегралы измеримых функций на пространственной мерой.
Наборы меры 0, называемые нулевыми наборами, незначительны. Соответственно, «изоморфизм по модулю 0» определяется как изоморфизм между подмножествами полной меры (то есть с незначительным дополнением).
A вероятностное пространство - это пространство с мерой, в котором всего пространства равно 1. Произведение любого семейства (конечного или нет) вероятностных пространств является вероятностным пространством. Напротив, для пространств с мерой в целом определяется только результат конечного числа пространств. Соответственно, существует множество бесконечномерных вероятностных мер (особенно гауссовских мер ), но нет бесконечномерных мер Лебега.
Стандартные вероятностные пространства особенно полезны. В стандартном вероятностном пространстве условное ожидание рассматривать как интеграл по условной мере (обычные условные вероятности, см. Также дезинтеграция меры ). Для двух стандартных вероятностных пространств каждый гомоморфизм их алгебр с мерой индуцируется некоторым сохраняющим меру отображением. Каждая вероятностная мера на стандартном измеримом месте приводит к стандартному вероятностному пространству. Произведение придерживается (конечной или нет) стандартных вероятностных пространств является стандартным вероятностным пространством. Все неатомарные стандартные вероятностные пространства взаимно изоморфны по модулю 0; один из них - отрезок (0,1) с мерой Лебега.
Эти пространства менее геометрически. В частности, идея размерности, применимая (в той или иной форме) ко всем другим пространствам, не применима к измеримым, мерным и вероятностным пространствам.
Теоретическое изучение исчисления, известное как математический анализ, привело в начале 20 века к рассмотрению линейных пространств действительных или комплексных функций. Самыми ранними примерами из них были функциональные пространства, каждый из которых адаптировано к своему классу проблем. Эти примеры широко распространены общими чертами, и вскоре эти особенности были перенесены в гильбертовы пространства, банаховы и более общие топологические пространства пространства. Это мощный инструментрий для решения широкого круга математических задач.
Наиболее подробную информацию несет класс пространств, называемый банаховыми алгебрами. Это банаховы пространства вместе с операцией непрерывного умножения. Важным ранним примером является ограниченных измеримых функций на пространстве с мерой X. Этот набор функций банаховым пространством относится к поточечного сложения и скалярного умножения. Благодаря операции поточечного умножения оно становится особым типом банахового пространства, которое теперь называется коммутативной алгеброй фон Неймана. Точечное умножение определяет представление этой алгебры в гильбертовом представлении функций, интегрируемых с квадратом на X. Раннее наблюдение Джона фон Неймана заключено в том, что это соответствует также работало в обратном направлении: при некоторых мягких гипотезах коммутативности фон Алгебра Неймана вместе с представлением в гильбертовом представлении определите пространство с мерой, и эти две конструкции (алгебры фон Неймана плюс и пространство с мерой) взаимно обратны.
Затем фон Нейман предположил, что некоммутативные алгебры фон Неймана имеют геометрический смысл, как это делают коммутативные алгебры фон Неймана. Вместе с Фрэнсисом Мюрреем он разработал классификацию алгебр фон Неймана. Конструкция прямого интеграла показывает, как разбить любую алгебру фон Неймана на набор более простых алгебр, называемых факторов. Фон Нейман и Мюррей разделили факторы на три типа. Тип I был почти идентичен коммутативному случаю. Типы II и III показали новые явления. Алгебра фон Неймана типа II определила геометрию с той особенностью, что размерность может быть любым неотрицательным действительным числом, а не только целым. Алгебры типа III не были ни типами I, ни II, и после нескольких десятилетий усилия было доказано, что они связаны с факторами типа II.
Немного другого подхода к геометрии функциональных пространств, используйте в то же время, что и работа фон Неймана и Мюррея по классификации факторов. Этот подход является теорией C * -алгебр. Здесь мотивирующим примером является C * -алгебра 
Оба этих примера теперь являются случаями поля, называемого некоммутативной геометрией. Конкретные примеры алгебр фон Неймана и C * -алгебр известны как некоммутативная теория меры и некомативная топология соответственно. Некоммутативная геометрия - это не просто стремление к общности ради нее самой и не просто любопытство. Некоммутативные пространства естественным образом и даже неизбежно возникают из некоторых конструкций. Например, рассмотрим непериодические мозаики Пенроуза плоскости воздушными змеями и дротиками. Теорема гласит, что в таком тайлинге каждый конечный фрагмент воздушных змеев и дротиков появляется бесконечно часто. Как следствие, невозможно различить две мозаики Пенроуза, глядя на конечную часть. Это делает невозможным присвоение множеству всех мозаик топологии в традиционном смысле. Несмотря на это, мозаики Пенроуза определяет некоммутативную C * -алгебру, и, следовательно, они могут быть изучены методами некоммутативной геометрии. Другой пример, представляющий большой интерес в динамической геометрии, происходит из слоений разнообразий. Это различные способы разбиения на подмногообразия большого размера. Набор всех листьев можно превратить в топологическое пространство. Однако пример иррационального вращения показывает, что это топологическое пространство может быть недоступно для техники классической теории меры. Простое геометрическое пространство, связанное с пространственным пространством.
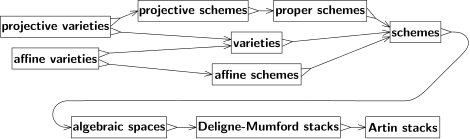Рис. 10: Отношения между математическими пространствами: схемами, стеками и т. Д. Алгебраическая геометрия изучает геометрические свойства полиномиальных соотношений. Полиномы - это тип функции, определяемый арифметическими операциями сложения и умножения. Из-за этого они связаны с алгеброй. Алгебраическая геометрия предлагает способ геометрических методов к вопросам чистой алгебры и наоборот.
До 1940-х годов алгебраическая геометрия работала исключительно над комплексными числами, и наиболее фундаментальной разновидностью было проективное пространство. Геометрия проективного пространства связывает с теорией перспективы, а ее алгебра описывается однородными многочленами. Все остальные разновидности были выявлены как подмножества проективного пространства. Проективные многообразия - это подмножества, определяемые набором однородных многочленов. В каждой точке проективного многообразия все многочлены в наборе должны быть равняться нулю. Дополнение нулевого множества линейного многочлена - это аффинное пространство, аффинное множество - это пересечение проективного множества с аффинным пространством.
Андре Вейль видел, что геометрические рассуждения иногда в теоретико-числовых ситуациях, когда рассматриваемые пространства могут быть дискретными или даже конечными. Преследуя эту идею, Вейль переписал основы алгебраической геометрии, освободил алгебраическую геометрию от ее зависимости от комплексных чисел и введя абстрактные алгебраические множества вложений, которые не были в проективном пространстве. Теперь это просто разновидности.
Тип, лежащий в основе самой современной алгебраической геометрии, даже более общий, чем абстрактные алгебраические многообразия Вейля. Она была введена Александром Гротендиком и называется схемой. Одним из мотивов теории является схематично, что многочлены необычно структурированы среди функций, и, следовательно, алгебраические множества являются жесткими. Это создает проблемы при попытке изучить вырожденные ситуации. Например, почти любая пара точек на окружности определяет уникальную линию, называемую секущей линией, и когда две точки движутся по окружности, секущая линия непрерывно действует. Однако, когда две точки сталкиваются, секущая линия вырождается в касательную. Касательная линия уникальна, нория этой конфигурации - единственная точка на окружности -недостаточно выразительна, чтобы определить уникальную линию. Изучение подобных ситуаций требует теории, способной назначать дополнительные данные для вырожденных действий.
Одним из строительных блоков схемы является топологическое пространство. Топологические пространства имеют непрерывные функции, но непрерывные функции слишком общие, чтобы отразить лежащую в основе интересующую алгебраическую функцию. Следовательно, другой компонент схемы - это пучок в топологическом пространстве, называемый «структурным пучком». На каждом открытом подмножестве топологического пространства пучок определяет набор функций, называемых «регулярными функциями». Топологическое пространство и структурный пучок вместе удовлетворяют условиям, которые означают, что функционируют из алгебраических операций.
Подобно разнообразия, схемы как пространства, локально моделируются на основе знакомого пространства. В случае многообразий знакомое пространство - это евклидово пространство. Для схемы локальные модели называются аффинными схемами. Аффинные схемы обеспечивают прямую связь между алгебраической геометрией и коммутативной алгеброй. Основными объектами изучения коммутативной алгебры являются коммутативные кольца. Если 
Есть много схем, которые не являются аффинными. В частности, проективные пространства удовлетворяют условию правильность, которое аналогично компактности. Аффинные схемы не могут быть собственными (за исключением тривиальных ситуаций, например, когда схема имеет только одну точку), и, следовательно, никакое проективное пространство не является аффинной схемой (за исключением нульмерных проективных пространств). Проективные схемы, то есть те, которые возникают как замкнутые подсхемы проективного пространства, являются единственным наиболее важным семейством схем.
Было введено несколько обобщений схем. Майкл Артин определил алгебраическое пространство как фактор схемы по отношениям эквивалентности, которые определяют этальные морфизмы. Алгебраические пространства сохраняют многие полезные свойства схем, одновременно будучи более гибкими. Например, теорема Киля – Мори может использоваться, чтобы показать, что многие пространства модулей являются алгебраическими пространствами.
Более общим, чем алгебраическое пространство, является стек Делиня – Мамфорда. Стеки DM похожи на схемы, но они допускают особенности, которые не могут быть описаны только в терминах полиномов. Они играют ту же роль для схем, что и орбифолды для многообразий. Например, факторное отношение аффинной плоскости к конечной группе вращений вокруг начала координат дает стек Делиня – Мамфорда, который не является схемой или алгебраическим пространством. Вдали от начала координат фактор по действию группы идентифицирует конечные наборы равноотстоящих точек на окружности. Но в начале координат круг состоит только из одной точки, самого начала, и действие группы фиксирует эту точку. Однако в стеке частных DM эта точка имеет дополнительные данные о частном. Такая уточненная структура полезна в теории пространств модулей, и фактически она была первоначально введена для описания модулей алгебраических кривых.
Дальнейшим обобщением являются алгебраические стеки, также называемые Стеки Артина. Стеки DM ограничены факторами по действиям конечной группы. Хотя этого достаточно для многих задач теории модулей, это слишком ограничительно для других, и стеки Артина допускают более общие факторы.
Рис. 11: Отношения между математическими пространствами: локали, топои и т. Д. В работе Гротендика над гипотезами Вейля он представил новый тип топологии, теперь называемый топологией Гротендика. Топологическое пространство (в обычном смысле) аксиоматизирует понятие «близости», делая две точки близкими тогда и только тогда, когда они лежат во многих из одних и тех же открытых множеств. Напротив, топология Гротендика аксиоматизирует понятие «покрытия». Покрытие пространства - это набор подпространств, которые вместе содержат всю информацию окружающего пространства. Поскольку пучки определены в терминах покрытий, топологию Гротендика можно также рассматривать как аксиоматизацию теории пучков.
Работа Гротендика над его топологиями привела его к теории тополей. В своих мемуарах Récoltes et Semailles он назвал их своей «самой обширной концепцией». Пучок (либо в топологическом пространстве, либо по топологии Гротендика) используется для выражения локальных данных. Категория всех связок содержит все возможные способы выражения локальных данных. Поскольку топологические пространства построены из точек, которые сами по себе являются своего рода локальными данными, категорию пучков можно использовать как замену исходному пространству. Следовательно, Гротендик определил топос как категорию пучков и изучал топос как самостоятельные объекты интереса. Теперь они называются Grothendieck topoi.
Каждое топологическое пространство определяет топос, и наоборот. Существуют топологические пространства, в которых при взятии связанных топосов теряется информация, но они обычно считаются патологическими. (Необходимым и достаточным условием является то, что топологическое пространство является трезвым пространством.) И наоборот, существуют топосы, ассоциированные топологические пространства которых не захватывают исходные топосы. Но эти топои далеко не патологические, они могут представлять большой математический интерес. Например, теория этальных когомологий Гротендика (которая в конечном итоге привела к доказательству гипотез Вейля) может быть сформулирована как когомологии этальных топосов схемы, и этот топос не исходит из топологического пространства.
Топологические пространства на самом деле приводят к очень специфическим топоям, называемым locales. Набор открытых подмножеств топологического пространства определяет решетку . Аксиомы топологического пространства делают эти решетки полными алгебрами Гейтинга. Теория локалей берет это за отправную точку. Локаль определяется как полная алгебра Гейтинга, и элементарные свойства топологических пространств повторно выражаются и опровергаются в этих терминах. Понятие локали оказывается более общим, чем топологическое пространство, в том смысле, что каждое трезвое топологическое пространство определяет уникальную локаль, но многие интересные локали происходят не из топологических пространств. Поскольку у локалей не обязательно должны быть точки, их изучение в шутку называется бессмысленной топологией.
Топои также демонстрируют глубокие связи с математической логикой. Каждый топос Гротендика имеет специальный пучок, называемый классификатором подобъектов. Этот классификатор подобъектов функционирует как набор всех возможных значений истинности. В топо множеств классификатор подобъектов - это набор 
Согласно Кевину Карлсону,
Тем не менее, общее определение «структуры» было предложено Бурбаки; он охватывает все типы пространств, упомянутые выше, (почти?) все типы математических структур, используемые до сих пор, и многое другое. Он дает общее определение изоморфизма и оправдывает перенос свойств между изоморфными структурами. Однако он никогда активно не использовался в математической практике (даже в математических трактатах, написанных самим Бурбаки). Вот последние фразы из рецензии Роберта Рида на книгу Лео Корри:
Для получения дополнительной информации о математические структуры см. Википедию: математическая структура, эквивалентные определения математических структур и транспорт структуры.
Иногда различие между геометрическими «пространствами» и алгебраическими «структурами» ясный, иногда неуловимый. Ясно, что группы являются алгебраическими, а евклидовы пространства геометрическими. Модули над кольцами так же алгебраичны, как и группы. В частности, когда кольцо выглядит как поле, модуль выглядит как линейное пространство ; это алгебраическое или геометрическое? В частности, когда оно является конечномерным, над действительными числами и снабжено внутренним произведением, оно становится евклидовым пространством ; теперь геометрический. Поле (алгебраическое?) вещественных чисел совпадает с (геометрической?) действительной линией. Его алгебраическое замыкание, (алгебраическое?) поле комплексных чисел, совпадает с (геометрическим?) комплексной плоскостью. Это прежде всего «место, где мы занимаемся анализом » (а не алгеброй или геометрией).
Каждое пространство, рассматриваемое в разделе «Типы пространств » выше, за исключением подразделов «Некоммутативная геометрия», «Схемы» и «Топои», является набором («основная база набор »конструкции, по Бурбаки) наделен некоторой дополнительной структурой; элементы базового набора обычно называют «точками» этого пространства. Напротив, элементы (базового набора) алгебраической структуры обычно не называют «точками».
Однако иногда используется более одного основного базового набора. Например, двумерная проективная геометрия может быть формализована с помощью двух базовых наборов, набора точек и набора линий. Кроме того, поразительной особенностью проективных плоскостей является симметрия ролей, которые играют точки и прямые. Менее геометрический пример: граф может быть формализован с помощью двух базовых наборов, набора вершин (называемых также узлами или точками) и набора ребер (также называемых дугами или линиями). Обычно конечное число основных базовых множеств и конечное число вспомогательных базовых множеств предусмотрено Бурбаки.
Многие математические структуры геометрического типа, рассматриваемые в подразделах «Некоммутативная геометрия», «Схемы» и «Топои» выше, не предусматривают базовый набор точек. Например, «бессмысленная топология » (другими словами, бесточечная топология или теория локали) начинается с единственного базового набора, элементы которого имитируют открытые множества в топологическом пространстве (но не являются наборами точек) ; см. также меротопология и геометрия без точек.
(с его тензорным произведением σ- алгебра) имеет измеримую структуру, которая не порождается топологией. Блестящее доказательство можно найти в этот ответ на MathOverflow.
Эта статья была отправлена в WikiJournal of Science для внешней академической рецензии. в 2017 г. (отчеты рецензентов ). Обновленный контент был повторно интегрирован на страницу Википедии под лицензией CC-BY-SA-3.0 (). Рассматриваемая версия записи: Борис Цирельсон ; и другие. (2018), «Пространства в математике» (PDF), WikiJournal of Science, 1 (1): 2, doi : 10.15347 / WJS /2018.002, Викиданные Q55120290
СМИ, связанные с Космосом (математика) на Wikimedia Commons