Аксиомы Тарского

Эта статья посвящена аксиомам евклидовой геометрии. Чтобы узнать о других значениях, см. Теорию множеств Тарского – Гротендика.

Аксиомы Тарского, из - за Альфреда Тарского, являются аксиомой набор для значительного фрагмента евклидовой геометрии, которая formulable в логике первого порядка с идентичностью, и не требующий теории множеств ( Тарского 1959) (т.е. та часть евклидовой геометрии, которая является formulable как элементарная теория ). Другое современное axiomizations евклидовой геометрии аксиома Гильберта и аксиомы Биркгоф.

• 1 Обзор
• 2 Аксиомы
  • 2.1 Основные отношения
  • 2.2 Аксиомы конгруэнтности
    • 2.2.1 Комментарий
  • 2.3 Аксиомы промежуточности
  • 2.4 Соответствие и промежуточность
• 3 Обсуждение
• 4 Сравнение с Гильбертом
• 5 См. Также
• 6 Примечания
• 7 ссылки

В начале своей карьеры Тарский преподавал геометрию и исследовал теорию множеств. Его коллега Стивен Гивант (1999) объяснил отправную точку Тарского:

От Энрикеса Тарский узнал о работе Марио Пиери, итальянского геометра, на которого сильно повлиял Пеано. Тарский предпочитал систему Пиери [из его мемуаров « Точка и сфера»), в которой логическая структура и сложность аксиом были более прозрачными.

Затем Гивант говорит, что «с типичной тщательностью» Тарский разработал свою систему:

Чем отличался подход Тарского к геометрии? Во-первых, система аксиом была намного проще любой из существовавших до того времени систем аксиом. На самом деле длина всех аксиом Тарского, вместе взятых, не намного больше, чем просто одна из 24 аксиом Пиери. Это была первая система евклидовой геометрии, которая была достаточно простой, чтобы все аксиомы могли быть выражены в терминах только примитивных понятий, без помощи определенных понятий. Что еще более важно, впервые было проведено четкое различие между полной геометрией и ее элементарной, то есть ее частью первого порядка.

Как и другие современные аксиоматизации евклидовой геометрии, Тарский использует формальную систему, состоящую из цепочек символов, называемых предложениями, конструкция которых соблюдает формальные синтаксические правила, и правила доказательства, которые определяют разрешенные манипуляции с предложениями. В отличие от некоторых других современных аксиоматизаций, таких как аксиоматизация Биркгофа и Гильберта, аксиоматизация Тарского не имеет примитивных объектов, кроме точек, поэтому переменная или константа не могут относиться к линии или углу. Поскольку точки являются единственными примитивными объектами, и поскольку система Тарского является теорией первого порядка, невозможно даже определить линии как наборы точек. Единственными примитивными отношениями ( предикатами ) являются «промежуточность» и «соответствие» между точками.

Аксиоматизация Тарского короче, чем ее конкуренты, в том смысле, в котором Тарский и Гивант (1999) явно указывают на это. Он более краток, чем у Пиери, потому что у Пиери было только два примитивных понятия, в то время как Тарский ввел три: точка, промежуточность и конгруэнтность. Такая экономия примитивных и определенные понятия означают, что система Тарская не очень удобно для ведения евклидовой геометрии. Скорее, Тарский разработал свою систему, чтобы облегчить ее анализ с помощью инструментов математической логики, то есть облегчить вывод ее метаматематических свойств. Система Тарского обладает необычным свойством: все предложения могут быть записаны в универсально-экзистенциальной форме, частном случае пренексной нормальной формы. Эта форма имеет все универсальные кванторы, предшествующие любым кванторам существования, так что все предложения могут быть преобразованы в форму. Этот факт позволил Тарскому доказать, что евклидова геометрия разрешима : существует алгоритм, который может определить истинность или ложность любого предложения. Аксиоматизация Тарского также завершена. Это не противоречит первой теореме Гёделя о неполноте, потому что теории Тарского не хватает выразительной силы, необходимой для интерпретации арифметики Робинсона ( Franzén 2005: 25–26). ${\ displaystyle \ forall u \ forall v \ ldots \ exists a \ exists b \ dots.}$

Альфред Тарский работал над аксиоматизацией и метаматематикой евклидовой геометрии с перерывами с 1926 года до своей смерти в 1983 году, причем Тарский (1959) возвещал о его зрелом интересе к этому предмету. Работа Тарского и его учеников по евклидовой геометрии достигла высшей точки в монографии Schwabhäuser, Szmielew, and Tarski (1983), в которой изложены 10 аксиом и одна схема аксиом, показанные ниже, связанная с ними метаматематика и изрядная часть предмета. Гупта (1965) внес важный вклад, а Тарски и Гивант (1999) обсуждают историю.

Фундаментальные отношения

Эти аксиомы представляют собой более элегантную версию набора, разработанного Тарским в 1920-х годах в рамках своего исследования метаматематических свойств геометрии евклидовой плоскости. Эта цель потребовала переформулировать эту геометрию как теорию первого порядка. Тарский сделал это полагание на вселенную из точек, прописными буквами, обозначающими переменных, пробегающих этой вселенной. Равенство обеспечивается базовой логикой (см. Логика первого порядка # Равенство и ее аксиомы ). Затем Тарский постулировал два примитивных отношения:

• Между, тройственное отношение. Атомарное предложение Bxyz означает, что у является «между» х и г, другими словами, что у есть точка на сегменте линии XZ. (Это отношение интерпретируется включительно, так что Bxyz тривиально истинно всякий раз, когда x = y или y = z).
• Конгруэнтность (или «равноудаленность»), тетрадное отношение. Атомарное предложение WX ≡ уг можно интерпретировать как WX есть конгруэнтны с уг, другими словами, что длина отрезка линии Wx равна длине отрезка уг.

Промежуточность отражает аффинный аспект евклидовой геометрии; конгруэнтность, ее метрический аспект. Фоновая логика включает идентичность, бинарное отношение. Аксиомы вызывают идентичность (или ее отрицание) пять раз.

Приведенные ниже аксиомы сгруппированы по типам вызываемых ими отношений, а затем отсортированы сначала по количеству экзистенциальных кванторов, а затем по количеству элементарных предложений. Аксиомы следует рассматривать как универсальные замыкания ; следовательно, любые свободные переменные следует рассматривать как неявно универсально определяемые количественно.

Аксиомы конгруэнтности

Рефлексивность конгруэнтности

${\ Displaystyle ху \ эквив ух \,.}$

Идентичность конгруэнтности

${\ Displaystyle xy \ Equiv zz \ ​​rightarrow x = y.}$

Транзитивность сравнения

${\ Displaystyle (ху \ эквив цу \ земля ху \ экв vw) \ rightarrow цу \ эквив vw.}$

Комментарий

Хотя отношение конгруэнтности формально является четырехсторонним отношением между точками, его также можно неформально рассматривать как бинарное отношение между двумя отрезками линии и. Приведенные выше аксиомы «Рефлексивности» и «Транзитивности», вместе взятые, доказывают оба: ${\ Displaystyle ху \ эквив zw}$${\ displaystyle xy}$${\ displaystyle zw}$

• что это бинарное отношение на самом деле является отношением эквивалентности
  • оно рефлексивно:.${\ Displaystyle ху \ эквив ху}$
  • это симметрично.${\ Displaystyle XY \ Equiv ZW \ Rightarrow ZW \ Equiv XY}$
  • это переходно.${\ Displaystyle (ху \ эквив цу \ земля цу \ эквиввв) \ правая стрелка ху \ эквиввв}$
• и что порядок, в котором указаны точки линейного сегмента, не имеет значения.
  • ${\ Displaystyle ху \ эквив zw \ rightarrow ху \ эквивалент wz}$.
  • ${\ Displaystyle ху \ эквив zw \ rightarrow yx \ эквив zw}$.
  • ${\ Displaystyle ху \ эквив zw \ rightarrow yx \ эквив wz}$.

Аксиома «транзитивности» утверждает, что конгруэнтность евклидова в том смысле, что она уважает первое из « общих понятий » Евклида.

Аксиома «Тождество конгруэнтности» интуитивно утверждает, что если xy конгруэнтно отрезку, который начинается и заканчивается в одной и той же точке, x и y являются одной и той же точкой. Это тесно связано с понятием рефлексивности для бинарных отношений.

Аксиомы промежуточности

Аксиома Паша

Идентичность посредничества

${\ displaystyle Bxyx \ rightarrow x = y.}$

Единственная точка на отрезке - это он сам. ${\ displaystyle xx}$${\ displaystyle x}$

Аксиома Паши

${\ displaystyle (Bxuz \ land Byvz) \ rightarrow \ существует \, (Buay \ land Bvax).}$

Непрерывность: φ и ψ делят луч на две половины, и аксиома утверждает, что существует точка b, разделяющая эти две половины.

Схема аксиомы непрерывности

Пусть φ ( x) и ψ ( y) - формулы первого порядка, не содержащие свободных экземпляров ни a, ни b. Пусть также нет свободных экземпляров x в ψ ( y) или y в φ ( x). Тогда все экземпляры следующей схемы являются аксиомами:

${\ Displaystyle \ существует a \, \ forall x \, \ forall y \, [(\ phi (x) \ land \ psi (y)) \ rightarrow Baxy] \ rightarrow \ существует b \, \ forall x \, \ forall y \, [(\ phi (x) \ land \ psi (y)) \ rightarrow Bxby].}$

Пусть r - луч с концом a. Пусть формулы первого порядка φ и ψ определяют подмножества X и Y в r, так что каждая точка в Y находится справа от каждой точки X (относительно a). Тогда существует точка Ь в г, лежащую между X и Y. По сути, это конструкция разреза Дедекинда, выполняемая таким образом, чтобы избежать количественной оценки по множествам.

Нижнее измерение

${\ Displaystyle \ существует а \, \ существует b \, \ существует с \, [\ neg Babc \ land \ neg Bbca \ land \ neg Bcab].}$

Существуют три неколлинеарные точки. Без этой аксиомы теория могла бы быть смоделирована одномерной действительной линией, единственной точкой или даже пустым множеством.

Конгруэнтность и промежуточность

Верхнее измерение

Верхнее измерение

${\ Displaystyle (xu \ эквив xv \ земля ю \ эквив yv \ земля цу \ эквив zv \ земля и \ neq v) \ rightarrow (Bxyz \ lor Byzx \ lor Bzxy).}$

Три точки, равноудаленные от двух разных точек, образуют линию. Без этой аксиомы теория могла бы быть смоделирована трехмерным или многомерным пространством.

Аксиома Евклида

Каждый из трех вариантов этой аксиомы, эквивалентных по сравнению с остальными аксиомами Тарского параллельному постулату Евклида, имеет преимущество перед другими:

• A обходится без квантификаторов существования ;
• B имеет наименьшее количество переменных и элементарных предложений ;
• C требует только одного примитивного понятия - промежуточности. Этот вариант обычно приводится в литературе.

А:${\ Displaystyle ((Bxyw \ земля ху \ эквив yw) \ земля (Bxuv \ земля ху \ экв уф) \ земля (Бюз \ земля ю \ экв зу)) \ rightarrow yz \ эквив vw.}$

Пусть отрезок прямой соединяется с серединой двух сторон данного треугольника. Этот отрезок будет вдвое короче третьей стороны. Это эквивалентно суммированию внутренних углов любого треугольника с двумя прямыми углами.

B:${\ Displaystyle Bxyz \ лор Byzx \ лор Bzxy \ лор \ существует а \, (ха \ эквив я \ земля ха \ эквив za).}$

Для любого треугольника существует круг, включающий все его вершины.

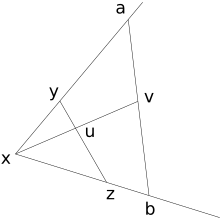Аксиома Евклида: C

C:${\ displaystyle (Bxuv \ land Byuz \ land x \ neq u) \ rightarrow \ exists a \, \ exists b \, (Bxya \ land Bxzb \ land Bavb).}$

Для любого угла и любой точки v внутри существует отрезок прямой, включающий v, с конечными точками на каждой стороне угла.

Пять сегментов

Пять сегментов

${\ Displaystyle {(х \ neq y \ земля Bxyz \ земля Bx'y'z '\ земля ху \ экв x'y' \ земля yz \ эквив y'z '\ земля ху \ эквив x'u' \ земля ю \ Equiv y'u ')} \ rightarrow zu \ Equiv z'u'.}$

Начнем с двух треугольников, xuz и x'u'z. Нарисуйте отрезки yu и y'u ', соединяя вершину каждого треугольника с точкой на стороне, противоположной вершине. В результате получаются два разделенных треугольника, каждый из которых состоит из пяти сегментов. Если четыре сегмента одного треугольника конгруэнтны сегменту другого треугольника, то пятые сегменты обоих треугольников должны быть конгруэнтными.

Это эквивалентно правилу стороны-угла-стороны для определения конгруэнтности двух треугольников; если углы uxz и u'x'z ' конгруэнтны (существуют конгруэнтные треугольники xuz и x'u'z'), и две пары инцидентных сторон конгруэнтны ( xu ≡ x'u ' и xz ≡ x'z '), то оставшаяся пара сторон также конгруэнтна ( uz ≡ u'z').

Строительство сегмента

${\ Displaystyle \ существует z \, [Bxyz \ land yz \ Equiv ab].}$

Для любой точки y можно провести в любом направлении (определяемом x) линию, совпадающую с любым отрезком ab.

Начиная с двух примитивных отношений, поля которых являются плотной вселенной из точек, Тарские построила геометрию сегментов линии. Согласно Тарски и Гиванту (1999: 192–93), ни одна из вышеперечисленных аксиом не является принципиально новой. Первые четыре аксиомы устанавливают некоторые элементарные свойства двух примитивных отношений. Например, рефлексивность и транзитивность конгруэнтности устанавливают, что конгруэнтность - это отношение эквивалентности на отрезках прямой. Тождество конгруэнтности и промежуточности управляет тривиальным случаем, когда эти отношения применяются к нечетким точкам. Теорема xy ≡ zz ↔ x = y ↔ Bxyx расширяет эти аксиомы тождества.

Ряд других свойств промежуточности можно вывести в виде теорем, в том числе:

• Рефлексивность : Bxxy  ;
• Симметрия : Bxyz → Bzyx  ;
• Транзитивность : ( Bxyw ∧ Byzw) → Bxyz  ;
• Связь : ( Bxyw ∧ Bxzw) → ( Bxyz ∨ Bxzy).

Последние два свойства полностью упорядочивают точки, составляющие линейный сегмент.

Верхний и нижний Dimension вместе требует, чтобы любая модель этих аксиом имеет конкретные конечную размерность. Соответствующие изменения в этих аксиомах дают наборы аксиом евклидовой геометрии для измерений 0, 1 и больше 2 (Tarski and Givant 1999: Axioms 8 ⁽¹⁾, 8 ⁽ⁿ⁾, 9 ⁽⁰⁾, 9 ⁽¹⁾, 9 ^{( п)}). Обратите внимание, что твердотельная геометрия не требует новых аксиом, в отличие от аксиом Гильберта. Более того, нижнее измерение для n измерений - это просто отрицание верхнего измерения для n - 1 измерений.

Когда количество измерений больше 1, промежуточность можно определить в терминах конгруэнтности (Tarski and Givant, 1999). Сначала определите отношение «≤» (где интерпретируется «длина линейного сегмента меньше или равна длине линейного сегмента »): ${\ displaystyle ab \ leq cd}$${\ displaystyle ab}$${\ displaystyle cd}$

${\ displaystyle xy \ leq zu \ leftrightarrow \ forall v (zv \ Equiv uv \ rightarrow \ exists w (xw \ Equiv yw \ land yw \ Equiv uv)).}$

В случае двух измерений интуиция такова: для любого отрезка xy линии рассмотрите возможный диапазон длин xv, где v - любая точка на серединном перпендикуляре к xy. Очевидно, что хотя нет верхней границы длины xv, существует нижняя граница, которая возникает, когда v является средней точкой xy. Таким образом, если xy короче или равен zu, то диапазон возможных длин xv будет надмножеством диапазона возможных длин zw, где w - любая точка на серединном перпендикуляре к zu.

Тогда промежуточность можно определить, используя интуицию, что кратчайшее расстояние между любыми двумя точками - это прямая линия:

${\ displaystyle Bxyz \ leftrightarrow \ forall u ((ux \ leq xy \ land uz \ leq zy) \ rightarrow u = y).}$

Схема аксиом непрерывности гарантирует, что порядок точек на прямой завершен (относительно определяемых свойств первого порядка). Аксиомы Паша и Евклида хорошо известны. Примечательно, что евклидова геометрия требует только следующих дополнительных аксиом:

• Строительство сегмента. Эта аксиома делает возможным измерение и декартову систему координат - просто присвойте значение 1 некоторому произвольному непустому отрезку линии;

Пусть wff обозначает правильно построенную формулу (или синтаксически правильную формулу) элементарной геометрии. Тарский и Гивант (1999: 175) доказали, что элементарная геометрия:

• Последовательно : не существует такого wff, что и оно, и его отрицание являются теоремами;
• Завершенность : каждое предложение или его отрицание - это теорема, доказываемая на основе аксиом;
• Разрешимость : существует алгоритм, который присваивает значение истинности каждому предложению. Это следует из Тарского:
  • Процедура принятия решения для реального замкнутого поля, которую он нашел методом исключения квантора ( теорема Тарского – Зайденберга );
  • Аксиомы, допускающие (многомерную) точную интерпретацию как реальное замкнутое поле.

Гупта (1965) доказал независимость вышеприведенных аксиом, за исключением Паша и Рефлексивности конгруэнтности.

Отрицание аксиомы Евклида дает гиперболическую геометрию, а полное ее исключение дает абсолютную геометрию. Полная (в отличие от элементарной) евклидова геометрия требует отказа от аксиоматизации первого порядка: замените φ ( x) и ψ ( y) в схеме аксиом Непрерывности на x ∈ A и y ∈ B, где A и B - переменные с универсальным количественным определением. ранжирование по наборам точек.

Аксиомы Гильберта для плоской геометрии номер 16 и включают транзитивность сравнения и вариант аксиомы Паша. Единственное понятие интуитивной геометрии, упоминаемое в замечаниях к аксиомам Тарского, - это треугольник. (Версии B и C аксиомы Евклида относятся к «кругу» и «углу» соответственно.) Аксиомы Гильберта также требуют «луча», «угла» и понятия треугольника, «включающего в себя» угол. Помимо промежуточности и конгруэнтности, аксиомы Гильберта требуют примитивного бинарного отношения «on», связывающего точку и линию. Схема аксиом непрерывности играет роль, аналогичную двум аксиомам непрерывности Гильберта. Эта схема незаменима; Евклидова геометрия на языке Тарского (или эквивалентного ему) не может быть аксиоматизирована с конечной аксиоматизацией как теория первого порядка. Аксиомы Гильберта не составляют теорию первого порядка, потому что его аксиомы непрерывности требуют логики второго порядка.

Первые четыре группы аксиом аксиом Гильберта для плоской геометрии можно интерпретировать двояко с аксиомами Тарского минус непрерывность.

• Евклидова геометрия
• Евклидово пространство

1. ^ Тарский и Givant, 1999, стр 177

• Францен, Торкель (2005), Теорема Гёделя: неполное руководство по ее использованию и злоупотреблениям, AK Peters, ISBN   1-56881-238-8
• Гивант, Стивен (1999) «Объединение нитей в работе Альфреда Тарски», Mathematical Intelligencer 21: 47–58.
• Гупта, HN (1965) Вклад в аксиоматические основы геометрии. Кандидат наук. защитил диссертацию в Калифорнийском университете в Беркли.
• Тарский, Альфред (1959), «Что такое элементарная геометрия?», Леон Хенкин, Патрик Суппес и Альфред Тарский (ред.), Аксиоматический метод. Особое внимание уделяется геометрии и физике. Материалы международного симпозиума в Univ. из Калифорнии, Беркли, 26 декабря 1957 г. - янв. 4, 1958, Исследования по логике и основам математики, Амстердам: Северная Голландия, стр. 16–29, MR   0106185. Доступно в виде переиздания 2007 г., Brouwer Press, ISBN   1-4437-2812-8
• Тарский, Альфред ; Givant, Стивен (1999), "Система Тарского геометрии", Бюллетень символической логики, 5 (2): 175-214, CiteSeerX   10.1.1.27.9012, DOI : 10,2307 / 421089, ISSN   1079-8986, JSTOR   421089, Руководство по ремонту   1791303
• Швабхойзер В., Шмилев В. и Альфред Тарский, 1983. Метаматематические методы в геометрии. Springer-Verlag.
• Щерба, LW (1986). «Тарский и геометрия». Журнал символической логики. 51 (4): 907–12. DOI : 10.2307 / 2273904. JSTOR   2273904.