Ограниченная вариация

редактировать

В математическом анализе функция ограниченной вариации, также известная как BV-функция, является вещественной -значной функцией, общая вариация которой ограничена (конечна): график функции Обладание этим свойством в точном смысле означает хорошее поведение. Для непрерывной функции одиночной переменной наличие ограниченного изменения означает, что расстояние вдоль направления y -axis, пренебрегая вкладом движения вдоль оси x, пройденное точкой точкой, движущейся по графику, имеет конечное значение. Для непрерывной функции нескольких переменных смысл определения такой же, за исключением того факта, что рассматриваемый непрерывный путь не может быть целым графиком данной функции (который в данном случае является гиперповерхностью case), но может быть каждое пересечение самого графа с гиперплоскостью (в случае функций двух переменных, плоскостью ), параллельной фиксированной ось x и ось y.

Функции ограниченной вариации - это в точности те функции, относительно которых можно найти интегралы Римана – Стилтьеса всех непрерывных функций.

Другая характеристика утверждает, что функции ограниченной вариации на компактном интервале - это в точности те функции f, которые можно записать как разность g - h, где и g, и h ограничены монотонно.

В В случае нескольких переменных функция f, определенная на открытом подмножестве Ω множества ℝ, называется ограниченной вариацией, если ее производная по распределению является векторнозначной конечной Мера Радона.

Одним из наиболее важных аспектов функций ограниченной вариации является то, что они образуют алгебру из разрывных функций, первая производная которых существует почти везде : в связи с этим они могут и часто используются для определения обобщенных решений нелинейных задач, включающих функционалы, обычные и уравнения в частных производных. в математике, физике и технике.

У нас есть следующие цепочки включений для функций над замкнутым, ограниченным в отрезок действительной прямой:

непрерывно дифференцируемый ⊆ липшицевский ⊆ абсолютно непрерывный ⊆ ограниченный вариант ⊆ дифференцируемый почти везде

Содержание

1 История
2 Формальное определение
- 2.1 Функции BV от одной переменной
- 2.2 Функции BV от нескольких переменных
- 2.3 Локальные функции BV
- 2.4 Обозначение
3 Основные свойства
- 3.1 Функции BV имеют только переходной тип или устранимые разрывы
- 3,2 V (·, Ω) полунепрерывно снизу на L (Ω)
- 3,3 BV (Ω) является банаховым пространством
- 3,4 BV (Ω) не разделимо
- 3,5 Цепное правило для BV-функций
- 3.6 BV (Ω) - банахова алгебра
4 Обобщения и расширения
- 4.1 Весовые BV-функции
- 4.2 SBV-функции
- 4.3 bv-последовательности
- 4.4 Меры ограниченных вариация
5 Примеры
6 Приложения
- 6.1 Математика
- 6.2 Физика и инженерия
7 См. также
8 Примечания
9 Ссылки
- 9.1 Исследования
- 9.2 Исторические ссылки
10 Внешние ссылки
- 10.1 Теория
- 10.2 Прочее

История

Согласно Борису Голубову, BV-функции одной переменной были впервые представлены Камиллой Джордан в статье (Jordan 1881) речь идет о сходимости ряда Фурье. Первый успешный шаг в обобщении этой концепции на функции нескольких переменных был сделан Леонидой Тонелли, которая в 1926 году представила класс непрерывных BV-функций (Cesari 1986, стр. 47 –48), чтобы расширить свой прямой метод для поиска решений проблем в вариационном исчислении более чем с одной переменной. Десять лет спустя, в (Cesari 1936), Ламберто Чезари изменил требование непрерывности в определении Тонелли на менее ограничительное требование интегрируемости, впервые получив класс функций ограниченной вариации многих переменных в его полной общности: как и Джордан до него, он применил эту концепцию для решения проблемы сходимости рядов Фурье, но для функций двух переменных. После него несколько авторов применили BV-функции для изучения рядов Фурье от нескольких переменных, геометрической теории меры, вариационного исчисления и математической физики. Ренато Каччопполи и Эннио де Джорджи использовали их для определения меры негладких границ наборов (дополнительную информацию см. В записи «Набор Caccioppoli »). Ольга Арсеньевна Олейник представила свой взгляд на обобщенные решения для нелинейных уравнений в частных производных как функций из пространства BV в статье (Олейник 1957), и смог построить обобщенное решение ограниченной вариации первого порядка уравнения в частных производных в статье (Олейник 1959): несколько лет спустя и Джоэл А.. Смоллер применил BV-функции к исследованию единственного нелинейного гиперболического уравнения с частными производными первого порядка в статье (Conway Smoller 1966), доказав, что решение задача Коши для таких уравнений является функцией ограниченной вариации при условии, что начальное значение принадлежит к тому же классу. Айзик Исаакович Вольперт широко разработал исчисление для BV-функций: в статье (Vol'pert 1967) он доказал цепное правило для BV-функций и в В книге (Худжаев и Вольперт 1985) он вместе со своим учеником широко исследовал свойства BV-функций и их применение. Его формула цепного правила позже была расширена Луиджи Амбросио и Джанни Даль Мазо в статье (Амбросио и Даль Мазо 1990).

Формальное определение

BV функции одной переменной

Определение 1.1. Общая вариация непрерывной действительной -значной (или, в более общем смысле, комплексной -значной) функции f, определенной в интервал [a, b] ⊂ ℝ - это величина

V ab (f) = sup P ∈ P ∑ i = 0 n P - 1 | f (x i + 1) - f (x i) |. {\ displaystyle V_ {a} ^ {b} (f) = \ sup _ {P \ in {\ mathcal {P}}} \ sum _ {i = 0} ^ {n_ {P} -1} | f ( x_ {i + 1}) - f (x_ {i}) |. \,}

V_ {a} ^ {b} (f) = \ sup _ {{P \ in {\ mathcal {P}}}} \ sum _ {{i = 0}} ^ {{n _ {{P}} - 1}} | f (x _ {{i + 1}})) -f (x_ {i}) |. \,

где супремум берется по множеству $P = {P = {x 0,…, xn P} ∣ P является разделом [a, b], удовлетворяющим xi ≤ xi + 1 для 0 ≤ i ≤ n P - 1} {\ textstyle {\ mathcal {P}} = \ left \ {P = \ { x_ {0}, \ dots, x_ {n_ {P}} \} \ mid P {\ text {является разделом}} [a, b] {\ text {удовлетворяет}} x_ {i} \ leq x_ { i + 1} {\ text {for}} 0 \ leq i \ leq n_ {P} -1 \ right \}}$ ${\ textstyle {\ mathcal {P}} = \ left \ {P = \ {x_ {0}, \ dots, x_ {n_) {P}} \} \ mid P {\ text {является разделом}} [a, b] {\ text {удовлетворение}} x_ {i} \ leq x_ {i + 1} {\ text {for}} 0 \ leq i \ leq n_ {P} -1 \ right \}}$ из всех разделов рассматриваемого интервала.

Если f дифференцируемо и его производная интегрируема по Риману, его полная вариация является вертикальной составляющей длины дуги его графика, то есть,

V ab (f) = ∫ ab | f ′ (x) | d x. {\ displaystyle V_ {a} ^ {b} (f) = \ int _ {a} ^ {b} | f '(x) | \, \ mathrm {d} x.}

V_{a}^{b}(f)=\int _{a}^{b}|f'(x)|\,{\mathrm {d}}x.

Определение 1.2. Говорят, что непрерывная функция с действительным знаком $f {\ displaystyle f}$ $f$ на вещественной прямой имеет ограниченную вариацию (функция BV ) на выбранном интервале [a, b] ⊂ ℝ, если его полная вариация конечна, т.е.

f ∈ BV ([a, b]) ⟺ V ab (f) < + ∞ {\displaystyle f\in {\text{BV}}([a,b])\iff V_{a}^{b}(f)<+\infty }

{\ displaystyle f \ in {\ text {BV}} ([a, b]) \ iff V_ {a} ^ {b} (f) <+ \ infty}

Можно доказать, что действительная функция ƒ имеет ограниченную вариацию в $[a, b] {\ displaystyle [a, b]}$ $[a, b]$ тогда и только тогда, когда ее можно записать как разность ƒ = ƒ 1 - ƒ 2 двух неубывающих функций на $[a, b] {\ displaystyle [a, b]}$ $[a, b]$ : this результат известен как разложение Жордана функции и связан с разложением Жордана меры.

Через интеграл Стилтьеса, любая функция ограниченной вариации на отрезок [a, b] определяет линейный ограниченный функционал на C ([a, b]). В этом частном случае теорема о представлении Рисса – Маркова – Какутани утверждает, что каждый ограниченный линейный функционал возникает таким образом однозначно. Нормализованные положительные функционалы или вероятностные меры соответствуют положительным неубывающим нижним полунепрерывным функциям. Эта точка зрения была важна в спектральной теории, в частности в ее приложении к обыкновенным дифференциальным уравнениям.

BV-функциям нескольких переменных

Функции ограниченной вариации, BV функции, являются функциями, распределительная производная которых является конечной мерой Радона. Точнее:

Определение 2.1. Пусть $Ω {\ displaystyle \ Omega}$ $\ Omega$ будет открытым подмножеством ℝ. Функция $u {\ displaystyle u}$ $u$ , принадлежащая $L 1 (Ω) {\ displaystyle L ^ {1} (\ Omega)}$ $L ^ {1} (\ Omega)$ , называется ограниченной вариант (функция BV ) и записывается

u ∈ BV (Ω) {\ displaystyle u \ in BV (\ Omega)}

u \ in BV (\ Omega)

, если существует конечный вектор мера Радона $D u ∈ M (Ω, R n) {\ displaystyle \ scriptstyle Du \ in {\ mathcal {M}} (\ Omega, \ mathbb {R} ^ {n})}$ $\ scriptstyle Du \ in {\ mathcal M} (\ Omega, {\ mathbb {R}} ^ {n})$ такая, что выполняется следующее равенство

∫ Ω u (x) div ⁡ ϕ (x) dx = - ∫ Ω ⟨ϕ, D u (x) ⟩ ∀ ϕ ∈ С с 1 (Ω, R n) {\ displaystyle \ int _ {\ Omega} u (x) \ operatorname {div} {\ boldsymbol {\ phi}} (x) \, \ mathrm {d} x = - \ int _ {\ Omega} \ langle {\ boldsymbol {\ phi}}, Du (x) \ rangle \ qquad \ forall {\ boldsymbol {\ phi}} \ in C_ {c} ^ {1} ( \ Omega, \ mathbb {R} ^ {n})}

{\ displaystyle \ int _ {\ Omega} u (x) \ operatorname {div} {\ boldsymbol {\ phi}} (x) \, \ mathrm {d} x = - \ int _ {\ Omega} \ langle {\ boldsymbol {\ phi}}, Du (x) \ rangle \ qquad \ forall {\ boldsymbol {\ phi}} \ in C_ {c } ^ {1} (\ Omega, \ m athbb {R} ^ {n})}

, то есть $u {\ displaystyle u}$ $u$ определяет линейный функционал в пространстве $C c 1 (Ω, R n) {\ displaystyle \ scriptstyle C_ {c} ^ {1} (\ Omega, \ mathbb {R} ^ {n})}$ $\ scriptstyle C_ {c} ^ {1} (\ Omega, \ mathbb {R} ^ {n})$ из непрерывно ди различаемые векторные функции $ϕ {\ displaystyle \ scriptstyle {\ boldsymbol {\ phi}}}$ $\ scriptstyle {\ boldsymbol {\ phi}}$ из компактной опоры, содержащейся в $Ω {\ displaystyle \ Omega}$ $\ Omega$ : векторная мера $D u {\ displaystyle Du}$ $Du$ представляет, следовательно, распределительный или слабый градиент из $u {\ displaystyle u}$ $u$ .

BV может быть определен эквивалентно следующим образом.

Определение 2.2. Учитывая функцию $u {\ displaystyle u}$ $u$ , принадлежащую $L 1 (Ω) {\ displaystyle L ^ {1} (\ Omega)}$ $L ^ {1} (\ Omega)$ , общее изменение $u {\ displaystyle u}$ $u$ в $Ω {\ displaystyle \ Omega}$ $\ Omega$ определяется как

V (u, Ω): = sup { ∫ Ω u (x) div ⁡ ϕ (x) dx: ϕ ∈ C c 1 (Ω, R n), ‖ ϕ ‖ L ∞ (Ω) ≤ 1} {\ displaystyle V (u, \ Omega): = \ sup \ left \ {\ int _ {\ Omega} u (x) \ operatorname {div} {\ boldsymbol {\ phi}} (x) \, \ mathrm {d} x: {\ boldsymbol {\ phi}} \ в C_ {c} ^ {1} (\ Omega, \ mathbb {R} ^ {n}), \ \ Vert {\ boldsymbol {\ phi}} \ Vert _ {L ^ {\ infty} (\ Omega)} \ Leq 1 \ right \}}

{\ Displaystyle V (u, \ Omega): = \ sup \ left \ {\ int _ {\ Omega} u (x) \ operatorname {div} {\ boldsymbol {\ phi}} (x) \, \ mathrm {d} x: {\ boldsymbol {\ phi}} \ in C_ {c} ^ {1} (\ Omega, \ mathbb {R} ^ {n}), \ \ Vert {\ boldsymbol {\ phi}} \ Vert _ {L ^ {\ infty} (\ Omega)} \ leq 1 \ right \}}

где $‖ ‖ L ∞ (Ω) {\ displaystyle \ scriptstyle \ Vert \; \ Vert _ {L ^ {\ infty} (\ Omega)}}$ $\ scriptstyle \ Vert \; \ Vert _ {L ^ {\ infty} (\ Omega)}$ - Essential supremum norm. Иногда, особенно в теории множеств Каччопполи, используются следующие обозначения

∫ Ω | D u | Знак равно V (u, Ω) {\ displaystyle \ int _ {\ Omega} \ vert Du \ vert = V (u, \ Omega)}

\ int _ {\ Omega} \ vert Du \ vert = V (u, \ Omega)

, чтобы подчеркнуть, что $V (u, Ω) {\ displaystyle V (u, \ Omega)}$ $V (u, \ Omega)$ - это полная вариация распределительного / слабого градиента $и {\ displaystyle u}$ $u$ . Это обозначение также напоминает, что если $u {\ displaystyle u}$ $u$ принадлежит к классу $C 1 {\ displaystyle C ^ {1}}$ $C ^ {1 }$ (т.е. a непрерывная и дифференцируемая функция, имеющая непрерывную производные ), то ее вариация является в точности интегралом абсолютное значение его градиента.

Пространство функций ограниченной вариации (функций BV ) затем может быть определено как

BV ( Ω) = {u ∈ L 1 (Ω): V (u, Ω) < + ∞ } {\displaystyle BV(\Omega)=\{u\in L^{1}(\Omega)\colon V(u,\Omega)<+\infty \}}

BV (\ Omega) = \ {u \ in L ^ {1} (\ Omega) \ двоеточие V (u, \ Omega) <+ \ infty \}

Два определения эквивалентны, поскольку если $V (u, Ω) < + ∞ {\displaystyle \scriptstyle V(u,\Omega)<+\infty }$ $\ scriptstyle V (u, \ Omega) <+ \ infty$ , то

| ∫ Ω u (x) div ⁡ ϕ (x) d x | ≤ В (u, Ω) ‖ ϕ ‖ L ∞ (Ω) ∀ ϕ ∈ C c 1 (Ω, R n) {\ displaystyle \ left | \ int _ {\ Omega} u (x) \ operatorname {div} { \ boldsymbol {\ phi}} (x) \, \ mathrm {d} x \ right | \ leq V (u, \ Omega) \ Vert {\ boldsymbol {\ phi}} \ Vert _ {L ^ {\ infty} (\ Omega)} \ qquad \ forall {\ boldsymbol {\ phi}} \ in C_ {c} ^ {1} (\ Omega, \ mathbb {R} ^ {n})}

{\ displaystyle \ left | \ int _ {\ Omega} u (x) \ operatorname {div} {\ boldsymbol {\ phi}} (x) \, \ mathrm {d} x \ right | \ leq V (u, \ Omega) \ Vert {\ boldsymbol {\ phi}} \ Vert _ {L ^ {\ infty} (\ Omega)} \ qquad \ forall {\ boldsymbol {\ phi}} \ in C_ {c} ^ {1} (\ Omega, \ mathbb {R} ^ {n})}

поэтому $ϕ ↦ ∫ Ω u (x) div ⁡ ϕ (x) dx {\ textstyle {\ boldsymbol {\ phi}} \ mapsto \, \ int _ {\ Omega} u (x) \ operatorname {div} {\ boldsymbol {\ phi}} (x) \, dx}$ ${\ textstyle {\ boldsymbol {\ phi}} \ mapsto \, \ int _ {\ Omega} и (х) \ OperatorName {div} {\ boldsymbol {\ phi}} (x) \, dx}$ определяет непрерывный линейный функционал в пространстве $C c 1 (Ω, R n) {\ displaystyle \ scriptstyle C_ {c } ^ {1} (\ Omega, \ mathbb {R} ^ {n})}$ $\ scriptstyle C_ {c} ^ {1} (\ Omega, {\ mathbb {R}} ^ {n})$ . Поскольку $C c 1 (Ω, R n) ⊂ C 0 (Ω, R n) {\ displaystyle \ scriptstyle C_ {c} ^ {1} (\ Omega, \ mathbb {R} ^ {n}) \ подмножество C ^ {0} (\ Omega, \ mathbb {R} ^ {n})}$ $\ scriptstyle C_ {c} ^ {1} (\ Omega, {\ mathbb {R}} ^ {n}) \ подмножество C ^ {0} (\ Omega, {\ mathbb {R}} ^ {n})$ как линейное подпространство, этот непрерывный линейный функционал может быть расширенный непрерывно и линейно на все $C 0 (Ω, R n) {\ displaystyle \ scriptstyle C ^ {0} (\ Omega, \ mathbb {R} ^ {n})}$ $\ scriptstyle C ^ {0} (\ Omega, {\ mathbb { R}} ^ {n})$ по теореме Хана – Банаха. Следовательно, непрерывный линейный функционал определяет меру Радона по теореме о представлении Рисса – Маркова – Какутани.

Локально BV-функции

Если функциональное пространство локально интегрируемые функции, т.е. функции, принадлежащие $L loc 1 (Ω) {\ displaystyle \ scriptstyle L _ {\ text {loc}} ^ {1} (\ Omega) }$ ${\ displaystyle \ scriptstyle L _ {\ текст {loc}} ^ {1} (\ Omega)}$ , рассматривается в предыдущих определениях 1.2, 2.1и 2.2вместо одного из глобально интегрируемые функции, то определенное функциональное пространство - это пространство функций локально ограниченной вариации . Точно, развивая эту идею для определения 2.2, локальный вариант определяется следующим образом:

V (u, U) : = sup {∫ Ω u (x) div ⁡ ϕ (x) dx: ϕ ∈ C c 1 (U, R n), ‖ ϕ ‖ L ∞ (Ω) ≤ 1} {\ displaystyle V (u, U) : = \ sup \ left \ {\ int _ {\ Omega} u (x) \ operatorname {div} {\ boldsymbol {\ phi}} (x) \, \ mathrm {d} x: {\ boldsymbol {\ phi }} \ in C_ {c} ^ {1} (U, \ mathbb {R} ^ {n}), \ \ Vert {\ boldsymbol {\ phi}} \ Vert _ {L ^ {\ infty} (\ Omega)} \ leq 1 \ right \}}

{\ displaystyle V (u, U): = \ sup \ left \ {\ int _ {\ Omega} u (x) \ operatorname {div} {\ boldsymbol {\ phi}} (x) \, \ mathrm {d} x: {\ boldsymbol {\ phi}} \ in C_ {c} ^ {1} (U, \ mathbb {R} ^ {n}), \ \ Vert {\ boldsymbol {\ phi}} \ Vert _ {L ^ {\ infty} (\ Omega)} \ leq 1 \ right \}}

для каждого set $U ∈ O c (Ω) {\ displaystyle \ scriptstyle U \ in {\ mathcal {O}} _ {c } (\ Omega)}$ $\ scriptstyle U \ in {\ mathcal {O}} _ {c} (\ Omega)$ , определив $O c (Ω) {\ displaystyle \ scriptstyle {\ mathcal {O}} _ {c} (\ Omega)}$ $\ scriptstyle {\ mathcal {O} } _ {c} (\ Omega)$ как набор всех предкомпактных открытых подмножеств из $Ω {\ displaystyle \ Omega}$ $\ Omega$ относительно стандартной топологии конечномерные векторные пространства, и соответственно класс функций локально ограниченной вариации определяется как

BV lo c (Ω) = {u ∈ L loc 1 (Ω): V (u, U) < + ∞ ∀ U ∈ O c ( Ω) } {\displaystyle BV_{\text{loc}}(\Omega)=\{u\in L_{\text{loc}}^{1}(\Omega)\colon V(u,U)<+\infty \;\forall U\in {\mathcal {O}}_{c}(\Omega)\}}

{\ displaystyle BV _ {\ text {loc}} (\ Omega) = \ {u \ in L_ {\ text {loc}} ^ {1} (\ Omega) \ двоеточие V (u, U) <+ \ infty \; \ forall U \ in {\ mathcal {O}} _ {c} (\ Omega) \ }}

Обозначение

В основном существует два различных соглашения об обозначении пространств функций локально или глобально ограниченной вариации, и, к сожалению, они очень похожи: первая из них, принятая в этой записи, используется, например, в ссылках Giusti (1984) (частично), Hudjaev Vol'pert ( 1985) (частично), Giaquinta, Modica Souček (1998) и следующий

$BV (Ω) {\ displaystyle \ scriptstyle BV (\ Omega)}$ $\ scriptstyle BV (\ Omega)$ определяет пространство функций глобально ограниченной вариации
$BV loc (Ω) {\ displaystyle \ scriptstyle BV_ {loc} (\ Omega)}$ $\ scriptstyle BV _ {{loc}} (\ Omega)$ определяет пространство функций локально ограниченной вариации

Вторая, принятая в справочниках Вольперт (1967) и Мазья (1985) (частично), имеет следующий вид:

$BV ¯ (Ω) {\ displaystyle \ scriptstyle {\ overline {BV}} (\ Omega)}$ $\ scriptstyle \ overline {BV} (\ Omega)$ определяет пробел функций глобально ограниченной вариации
$BV (Ω) {\ displaystyle \ scriptstyle BV (\ Omega)}$ $\ scriptstyle BV (\ Omega)$ идентифицирует пробел функций локально ограниченных вариация

Основные свойства

Ниже будут рассматриваться только свойства, общие для функций одной переменной и функций нескольких переменных, а доказательства будут проводиться только для функций нескольких переменных, поскольку доказательство для случая одной переменной представляет собой прямую адаптацию случая нескольких переменных: кроме того, в каждом разделе будет указано, если свойство разделяется также функциями локально ограниченной вариации или нет. Ссылки (Giusti 1984, pp. 7–9), (Hudjaev Vol'pert 1985) и (Màlek et al. 1996) широко используются.

Функции BV имеют только скачкообразные или устраняемые разрывы

В случае одной переменной утверждение ясно: для каждой точки $x 0 {\ displaystyle x_ {0}}$ $x_ {0}$ в интервале $[a, b] ⊂ R {\ displaystyle [a, b] \ subset \ mathbb {R}}$ ${\ displaystyle [a, b] \ subset \ mathbb {R}}$ определения функция $u {\ displaystyle u}$ $u$ , верно одно из следующих двух утверждений

lim x → x 0 - u (x) = lim x → x 0 + u (x) {\ displaystyle \ lim _ {x \ rightarrow x_ {0 ^ {-}}} \! \! \! u (x) = \! \! \! \ lim _ {x \ rightarrow x_ {0 ^ {+ }}} \! \! \! u (x)}

\ lim _ {{x \ rightarrow x _ {{0 ^ {-}}}}} \! \! \! u (x) = \! \! \! \ lim _ { {x \ rightarrow x _ {{0 ^ {+}}}}} \! \! \! u (x)

lim x → x 0 - u (x) ≠ lim x → x 0 + u (x) {\ displaystyle \ lim _ {x \ rightarrow x_ { 0 ^ {-}}} \! \! \! U (x) \ neq \! \! \! \ Lim _ {x \ rightarrow x_ {0 ^ {+}}} \! \! \! U (x)}

\ lim _ {{x \ rightarrow x _ {{0 ^ {- }}}}} \! \! \! u (x) \ neq \! \! \! \ lim _ {{x \ rightarrow x _ {{0 ^ {+}}}}} \! \! \! u (x)

, в то время как оба предела существуют и конечны. В случае функций нескольких переменных необходимо понять некоторые предпосылки: во-первых, существует континуум из направлений, по которому можно приблизиться к заданной точке $x 0 {\ displaystyle x_ {0}}$ $x_ {0}$ , принадлежащий домену $Ω {\ displaystyle \ Omega}$ $\ Omega$ ⊂ℝ. Необходимо уточнить подходящую концепцию предела : выбор единичного вектора $a ^ ∈ R n {\ displaystyle \ scriptstyle {\ boldsymbol {\ hat {a} }} \ in \ mathbb {R} ^ {n}}$ $\ scriptstyle {{\ boldsymbol {{\ hat {a }}}}} \ in {\ mathbb {R}} ^ {n}$ можно разделить $Ω {\ displaystyle \ Omega}$ $\ Omega$ на два набора

Ω (a ^, x 0) = Ω ∩ {x ∈ R n | ⟨X - x 0, a ^⟩>0} Ω (- a ^, x 0) = Ω ∩ {x ∈ R n | ⟨Икс - Икс 0, - a ^⟩>0} {\ displaystyle \ Omega _ {({\ boldsymbol {\ hat {a}}}, {\ boldsymbol {x}} _ {0})} = \ Omega \ cap \ {{\ boldsymbol {x}} \ in \ mathbb {R} ^ {n} | \ langle {\ boldsymbol {x}} - {\ boldsymbol {x}} _ {0}, {\ boldsymbol {\ hat {a}}} \ rangle>0 \} \ qquad \ Omega _ {(- {\ boldsymbol {\ hat {a}}}, {\ boldsymbol {x}} _ {0})} = \ Omega \ cap \ {{\ boldsymbol {x}} \ in \ mathbb {R} ^ {n} | \ langle {\ boldsymbol {x}} - {\ boldsymbol {x}} _ {0}, - {\ boldsymbol {\ hat { a}}} \ rangle>0 \}}

\Omega _{{({{\boldsymbol {{\hat {a}}}}},{\boldsymbol {x}}_{0})}}=\Omega \cap \{{\boldsymbol {x}}\in {\mathbb {R}}^{n}|\langle {\boldsymbol {x}}-{\boldsymbol {x}}_{0},{{\boldsymbol {{\hat {a}}}}}\rangle>0 \} \ qquad \ Omega _ {{(- {{\ boldsymbol {{\ hat {a}}}}}, {\ boldsymbol {x }} _ {0})}} = \ Omega \ cap \ {{\ boldsymbol {x}} \ in {\ mathbb {R}} ^ {n} | \ langle {\ boldsymbol {x}} - {\ boldsymbol {x}} _ {0}, - {{\ boldsymbol {{\ hat {a}}}}} \ rangle>0 \}

Затем для каждой точки $x 0 {\ displaystyle x_ {0}}$ $x_ {0}$ принадлежащих область $Ω ∈ R n {\ displaystyle \ scriptstyle \ Omega \ in \ mathbb {R} ^ {n}}$ $\ scriptstyle \ Omega \ in {\ mathbb {R}} ^ {n}$ функции BV на $u {\ displaystyle u}$ $u$ верно только одно из следующих двух утверждений

lim x ∈ Ω (a ^, x 0) x → x 0 u (x) = lim Икс ∈ Ω (- а ^, Икс 0) Икс → Икс 0 U (Икс) {\ Displaystyle \ lim _ {\ overset {{\ boldsymbol {x}} \ rightarrow {\ boldsymbol {x}} _ {0}} {{\ boldsymbol {x}} \ in \ Omega _ {({\ boldsymbol {\ hat {a}}}, {\ boldsymbol {x}} _ {0})}}} \! \! \! \! \! \! u ({\ boldsymbol {x}}) = \! \! \! \! \! \! \! \ lim _ {\ overset {{\ boldsymbol {x}} \ rightarrow {\ boldsymbol {x }} _ {0}} {{\ boldsymbol {x}} \ in \ Omega _ {(- {\ boldsymbol {\ hat {a}}}, {\ boldsymbol {x}} _ {0})}}} \! \! \! \! \! \! \! u ({\ boldsymbol {x}})}

\ lim _ {{{\ overset {{\ boldsymbol {x}} \ rightarrow {\ boldsymbol {x}} _ {0}} {{\ boldsymbol {x}} \ in \ Omega _ {{({{\ boldsymbol {{\ hat {a}}}}}}, {\ boldsymbol {x}} _ {0})}}}}}} \! \! \! \! \! \! u ({\ boldsymbol {x}}) = \! \! \! \! \! \! \! \ lim _ {{{\ overset {{\ boldsymbol {x}} \ rightarrow {\ boldsymbol {x}} _ {0}} {{\ boldsymbol {x}} \ in \ Omega _ { {(- {{\ boldsymbol {{\ hat {a}}}}}, {\ boldsymbol {x}} _ {0})}}}}}} \! \! \! \! \! \! \ ! u ({\ boldsymbol {x}})

lim x ∈ Ω (a ^, x 0) x → x 0 u (x) ≠ lim x ∈ Ω (- а ^, Икс 0) Икс → Икс 0 U (Икс) {\ Displaystyle \ lim _ {\ overset {{\ boldsymbol {x}} \ rightarrow {\ boldsymbol {x}} _ {0}} { {\ boldsymbol {x}} \ in \ Omega _ {({\ boldsymbol {\ hat {a}}}, {\ boldsymbol {x}} _ {0})}}} \! \! \! \! \ ! \! u ({\ boldsymbol {x}}) \ neq \! \! \! \! \! \! \! \ lim _ {\ overset {{\ boldsymbol {x}} \ rightarrow {\ boldsymbol {x }} _ {0}} {{\ boldsymbol {x}} \ in \ Omega _ {(- {\ boldsymbol {\ ha t {a}}}, {\ boldsymbol {x}} _ {0})}}} \! \! \! \! \! \! \! u ({\ boldsymbol {x}})}

\ lim _ {{{\ overset {{\ boldsymbol {x}} \ rightarrow {\ boldsymbol {x}} _ {0}} {{\ boldsymbol {x}} \ in \ Omega _ {{({{\ boldsymbol {{\ hat {a}}) }}}, {\ boldsymbol {x}} _ {0})}}}}}} \! \! \! \! \! \! u ({\ boldsymbol {x}}) \ neq \! \! \! \! \! \! \! \ lim _ {{{\ overset {{\ boldsymbol {x}} \ rightarrow {\ boldsymbol {x}} _ {0}} {{\ boldsymbol {x}} \ in \ Omega _ {{(- {{\ boldsy mbol {{\ hat {a}}}}}, {\ boldsymbol {x}} _ {0})}}}}}} \! \! \! \! \! \! \! u ({\ boldsymbol {x}})

или $x 0 {\ displaystyle x_ {0}}$ $x_ {0}$ принадлежит подмножеству из $Ω {\ displaystyle \ Omega}$ $\ Omega$ , имеющему ноль $n - 1 {\ displaystyle n-1}$ $n-1$ -мерная мера Хаусдорфа. Величины

lim x ∈ Ω (a ^, x 0) x → x 0 u (x) = ua ^ (x 0) lim x ∈ Ω (- a ^, x 0) x → x 0 u (x) = U - a ^ (x 0) {\ displaystyle \ lim _ {\ overset {{\ boldsymbol {x}} \ rightarrow {\ boldsymbol {x}} _ {0}} {{\ boldsymbol {x}} \ в \ Omega _ {({\ boldsymbol {\ hat {a}}}, {\ boldsymbol {x}} _ {0})}}} \! \! \! \! \! \! u ({\ boldsymbol {x}}) = u _ {\ boldsymbol {\ hat {a}}} ({\ boldsymbol {x}} _ {0}) \ qquad \ lim _ {\ overset {{\ boldsymbol {x}} \ rightarrow { \ boldsymbol {x}} _ {0}} {{\ boldsymbol {x}} \ in \ Omega _ {(- {\ boldsymbol {\ hat {a}}}, {\ boldsymbol {x}} _ {0})}}} \! \! \! \! \! \! \! u ({\ boldsymbol {x}}) = u _ {- {\ boldsymbol {\ hat {a}}}} ({\ boldsymbol {x }} _ {0})}

\ lim _ {{{\ overset {{\ boldsymbol {x}} \ rightarrow {\ boldsymbol {x}} _ {0}} {{\ boldsymbol {x}} \ in \ Omega _ {{({ {\ boldsymbol {{\ hat {a}}}}}, {\ boldsymbol {x}} _ {0})}}}}}} \! \! \! \! \! \! u ({\ boldsymbol {x}}) = u _ {{{\ boldsymbol {{\ hat a}}}}} ({\ boldsymbol {x}} _ {0}) \ qquad \ lim _ {{{\ overset {{\ boldsymbol { x}} \ rightarrow {\ boldsymbol {x}} _ {0}} {{\ boldsymbol {x}} \ in \ Omega _ {{(- {{\ boldsymbol {{\ hat {a}}}}}, {\ boldsymbol {x}} _ {0})}}}}}} \! \! \! \! \! \! \! u ({\ boldsymbol {x}}) = u _ {{- {\ boldsymbol {{\ hat a}}}}} ({\ boldsymbol {x}} _ {0})

называются приблизительными пределами функции BV $u {\ displaystyle u}$ $u$ в точке $x 0 {\ displaystyle x_ {0}}$ $x_ {0}$ .

V (·, Ω) полунепрерывно снизу на L (Ω)

функциональное $V (⋅, Ω): BV (Ω) → R + {\ displaystyle \ scriptstyle V (\ cdot, \ Omega): BV (\ Omega) \ rightarrow \ mathbb {R} ^ {+}}$ $\ scriptstyl е V (\ cdot, \ Omega): BV (\ Omega) \ rightarrow {\ mathbb {R}} ^ {+}$ равно низкий эр полунепрерывный : чтобы увидеть это, выберите последовательность Коши BV-функций ${un} n ∈ N {\ displaystyle \ scriptstyle \ {u_ {n} \ } _ {n \ in \ mathbb {N}}}$ $\ scriptstyle \ {u_ {n} \} _ {{n \ in {\ mathbb {N}}}}$ сходится к $u ∈ L loc 1 (Ω) {\ displaystyle \ scriptstyle u \ in L _ {\ text {loc}} ^ {1} ( \ Omega)}$ $\ scriptstyle u \ in L _ {{\ text {loc}}} ^ {1} (\ Omega)$ . Тогда, поскольку все функции последовательности и их предельная функция интегрируемы и по определению нижнего предела

lim inf n → ∞ V (un, Ω) ≥ lim inf n → ∞ ∫ Ω un (x) div ϕ dx ≥ ∫ Ω lim n → ∞ un (x) div ϕ dx = ∫ Ω u (x) div ⁡ ϕ dx ∀ ϕ ∈ C c 1 (Ω, R n), ‖ ϕ ‖ L ∞ (Ω) ≤ 1 {\ displaystyle \ liminf _ {n \ rightarrow \ infty} V (u_ {n}, \ Omega) \ geq \ liminf _ {n \ rightarrow \ infty} \ int _ {\ Omega} u_ {n} (x) \ operatorname {div} \, {\ boldsymbol {\ phi}} \, \ mathrm {d} x \ geq \ int _ {\ Omega} \ lim _ {n \ rightarrow \ infty} u_ {n} (x) \ operatorname {div} \, {\ boldsymbol {\ phi}} \, \ mathrm {d} x = \ int _ {\ Omega} u (x) \ operatorname {div} {\ boldsymbol { \ phi}} \, \ mathrm {d} x \ qquad \ forall {\ boldsymbol {\ phi}} \ in C_ {c} ^ {1} (\ Omega, \ mathbb {R} ^ {n}), \ quad \ Vert {\ boldsymbol {\ phi}} \ Vert _ {L ^ {\ infty} (\ Omega)} \ leq 1}

{\ displaystyle \ liminf _ {n \ rightarrow \ infty} V (u_ {n}, \ Omega) \ geq \ liminf _ {n \ rightarrow \ infty} \ int _ {\ Omega} u_ {n} (x) \ operatorname {div} \, {\ boldsymbol {\ phi}} \, \ mathrm {d } x \ geq \ int _ {\ Omega} \ lim _ {n \ rightarrow \ infty} u_ {n} (x) \ operatorname {div} \, {\ boldsymbol {\ phi}} \, \ mathrm {d} x = \ int _ {\ Omega} u (x) \ operatorname {div} {\ boldsymbol {\ phi}} \, \ mathrm {d} x \ qquad \ forall {\ boldsymbol {\ phi}} \ in C_ { c} ^ {1} (\ Omega, \ mathbb {R} ^ {n}), \ quad \ Vert {\ boldsymbol {\ phi}} \ Vert _ {L ^ {\ infty} (\ Omega)} \ leq 1}

Теперь рассмотрим супремум на множестве функций $ϕ ∈ С с 1 (Ω, R N) {\ Displaystyle \ scriptstyle {\ boldsymbol {\ phi}} \ в C_ {c} ^ {1} (\ Omega, \ ma thbb {R} ^ {n})}$ $\ scriptstyle {\ boldsymbol {\ phi}} \ in C_ {c} ^ {1} (\ Omega, {\ mathbb {R}} ^ { n})$ такой, что $‖ ϕ ‖ L ∞ (Ω) ≤ 1 {\ displaystyle \ scriptstyle \ Vert {\ boldsymbol {\ phi}} \ Vert _ { L ^ {\ infty} (\ Omega)} \ leq 1}$ $\ scriptstyle \ Vert {\ boldsymbol {\ phi}} \ Верт _ {{L ^ {\ infty} (\ Omega)}} \ leq 1$ то выполняется следующее неравенство

lim inf n → ∞ V (un, Ω) ≥ V (u, Ω) {\ displaystyle \ liminf _ {n \ rightarrow \ infty} V (u_ {n}, \ Omega) \ geq V (u, \ Omega)}

\ liminf _ {{n \ rightarrow \ infty}} V (u_ {n}, \ Omega) \ geq V (u, \ Omega)

, что в точности соответствует определению полунепрерывности снизу.

BV ( Ω) является банаховым пространством

По определению $BV (Ω) {\ displaystyle BV (\ Omega)}$ $BV (\ Omega)$ является подмножеством из $L 1 (Ω) {\ displaystyle L ^ {1} (\ Omega)}$ $L ^ {1} (\ Omega)$ , а линейность следует из свойств линейности определяющего интеграла, т.е.

∫ Ω [u (x) + v (x)] div ⁡ ϕ (x) dx = ∫ Ω u (x) div ⁡ ϕ (x) dx + ∫ Ω v (x) div ⁡ ϕ (x) dx = = - Ω ⟨ϕ (x), D u (x)⟩ - ∫ Ω ⟨ϕ (x), D v (x)⟩ = - Ω ⟨ϕ (x), [D u (x) + D v (x)]⟩ {\ displaystyle {\ begin {align} \ int _ {\ Omega} [u (x) + v (x)] \ operatorname {div} {\ boldsymbol {\ phi}} (x) \, \ mathrm {d} x = \ int _ {\ Omega} u (x) \ operatorname {div} {\ boldsymbol {\ phi}} (x) \, \ mathrm {d} x + \ int _ {\ Omega } v (x) \ operatorname {div} {\ boldsymbol {\ phi}} (x) \, \ mathrm {d} x = \\ = - \ int _ {\ Omega} \ langle {\ boldsymbol {\ phi }} (x), Du (x) \ rangle - \ int _ {\ Omega} \ langle {\ boldsymbol {\ phi}} (x), Dv (x) \ rangle = - \ int _ {\ Omega} \ langle {\ boldsymbol {\ phi}} (x), [Du (x) + Dv (x)] \ rangle \ end {align}}}

{\ displaystyle {\ begin {align} \ int _ {\ Omega} [u (x) + v (x)] \ operatorname {div} {\ boldsymbol { \ phi}} (x) \, \ mathrm {d} x = \ int _ {\ Omega} u (x) \ operatorname {div} {\ boldsymbol {\ phi}} (x) \, \ mathrm {d} x + \ int _ {\ Omega} v (x) \ operatorname {div} {\ boldsymbol {\ phi}} (x) \, \ mathrm {d} x = \\ = - \ int _ {\ Omega} \ langle {\ boldsymbol {\ phi}} (x), Du (x) \ rangle - \ int _ {\ Omega} \ langle {\ boldsymbol {\ phi}} (x), Dv (x) \ rangle = - \ int _ {\ Omega} \ langle {\ boldsymbol {\ phi}} (x), [Du (x) + Dv (x)] \ rangle \ end {align}}}

для всех $ϕ ∈ C c 1 (Ω, R n) {\ displaystyle \ scriptstyle \ phi \ in C_ {c} ^ {1} (\ Omega, \ mathbb {R} ^ {n})}$ $\ scriptstyle \ phi \ in C_ {c} ^ {1} (\ Omega, {\ mathbb {R}} ^ {n})$ поэтому $u + v ∈ BV ( Ω) {\ displaystyle \ scriptstyle u + v \ in BV (\ Omega)}$ $\ scriptstyle u + v \ in BV (\ Omega)$ для всех $u, v ∈ BV (Ω) {\ displaystyle \ scriptstyle u, v \ in BV ( \ Omega)}$ $\ scriptstyle u, v \ in BV (\ Omega)$ и

∫ Ω c ⋅ u (x) div ⁡ ϕ (x) dx = c ∫ Ω u (x) div ⁡ ϕ (x) dx = - c ∫ Ω ⟨Φ (Икс), D U (Икс)⟩ {\ Displaystyle \ int _ {\ Omega} с \ CDOT и (х) \ OperatorName {div} {\ boldsymbol {\ phi}} (х) \, \ mathrm { d} x = c \ int _ {\ Omega} u (x) \ operatorname {div} {\ boldsymbol {\ phi}} (x) \, \ mathrm {d} x = -c \ int _ {\ Omega} \ langle {\ boldsymbol {\ phi}} (x), Du (x) \ rangle}

{\ displaystyle \ int _ {\ Omega} c \ cdot u (x) \ operatorname {div} {\ boldsymbol {\ phi}} (x) \, \ mathrm {d} x = c \ int _ {\ Omega} u (x) \ operatorname {div} {\ boldsymbol {\ phi}} (x) \, \ mathrm {d} x = -c \ int _ {\ Omega} \ langle {\ boldsymbol {\ phi}} (x), Du (x) \ rangle}

для всех $c ∈ R {\ displaystyle \ scriptstyle c \ in \ mathbb {R}}$ $\ scriptstyle c \ in {\ mathbb {R}}$ , следовательно, $cu ∈ BV (Ω) {\ displaystyle \ scriptstyle cu \ in BV (\ Omega)}$ $\ scriptstyle cu \ in BV (\ Omega)$ для всех $u ∈ BV (Ω) {\ displaystyle \ scriptstyle u \ in BV (\ Omega)}$ $\ scriptstyle u \ in BV (\ Omega)$ и все $c ∈ R {\ displaystyle \ scriptstyle c \ in \ mathbb {R}}$ $\ scriptstyle c \ in {\ mathbb {R}}$ . Доказанные свойства векторного пространства подразумевают, что $BV (Ω) {\ displaystyle BV (\ Omega)}$ $BV (\ Omega)$ является векторным подпространством из $L 1 (Ом) {\ Displaystyle L ^ {1} (\ Omega)}$ $L ^ {1} (\ Omega)$ . Теперь рассмотрим функцию $‖ ‖ BV: BV (Ω) → R + {\ displaystyle \ scriptstyle \ | \; \ | _ {BV}: BV (\ Omega) \ rightarrow \ mathbb {R} ^ {+} }$ $\ scriptstyle \ | \; \ | _ {{BV}}: BV (\ Omega) \ rightarrow {\ mathbb {R}} ^ {+}$ определяется как

‖ u ‖ BV: = ‖ u ‖ L 1 + V (u, Ω) {\ displaystyle \ | u \ | _ {BV}: = \ | u \ | _ {L ^ {1}} + V (u, \ Omega)}

\ | u \ | _ {{BV}}: = \ | u \ | _ {{L ^ {1}}} + V (u, \ Omega)

где $‖ ‖ L 1 {\ displaystyle \ scriptstyle \ | \; \ | _ {L ^ {1}}}$ $\ scriptstyle \ | \; \ | _ {{L ^ {1}}}$ - это обычный $L 1 (Ω) {\ displaystyle L ^ {1} (\ Omega)}$ $L ^ {1} (\ Omega)$ norm : легко доказать, что это норма на $BV (Ω) {\ displaystyle BV (\ Omega)}$ $BV (\ Omega)$ . Чтобы увидеть, что $BV (Ω) {\ displaystyle BV (\ Omega)}$ $BV (\ Omega)$ является полным по отношению к нему, т.е. это банахово пространство, рассмотрим последовательность Коши ${un} n ∈ N {\ displaystyle \ scriptstyle \ {u_ {n} \} _ {n \ in \ mathbb {N}}}$ $\ scriptstyle \ {u_ {n} \} _ {{n \ in {\ mathbb {N}}}}$ в $BV (Ω) {\ displaystyle BV (\ Omega)}$ $BV (\ Omega)$ . По определению это также последовательность Коши в $L 1 (Ω) {\ displaystyle L ^ {1} (\ Omega)}$ $L ^ {1} (\ Omega)$ и поэтому имеет предел $u {\ displaystyle u}$ $u$ в $L 1 (Ω) {\ displaystyle L ^ {1} (\ Omega)}$ $L ^ {1} (\ Omega)$ : поскольку $un { \ displaystyle u_ {n}}$ $u_ {n}$ ограничен в $BV (Ω) {\ displaystyle BV (\ Omega)}$ $BV (\ Omega)$ для каждого $n {\ displaystyle n}$ $n$ , затем $‖ u ‖ BV < + ∞ {\displaystyle \scriptstyle \Vert u\Vert _{BV}<+\infty }$ $\ scriptstyle \ Vert u \ Vert _ {{BV}} <+ \ infty$ на полунепрерывность снизу вариации $V (⋅, Ω) {\ displaystyle \ scriptstyle V (\ cdot, \ Omega)}$ $\ scriptstyle V (\ cdot, \ Omega)$ , поэтому $u {\ displaystyle u}$ $u$ является функцией BV. Наконец, снова с помощью полунепрерывности снизу, выбирая произвольное небольшое положительное число $ε {\ displaystyle \ scriptstyle \ varepsilon}$ $\ scriptstyle \ varepsilon$

‖ uj - uk ‖ BV < ε ∀ j, k ≥ N ∈ N ⇒ V ( u k − u, Ω) ≤ lim inf j → + ∞ V ( u k − u j, Ω) ≤ ε {\displaystyle \Vert u_{j}-u_{k}\Vert _{BV}<\varepsilon \quad \forall j,k\geq N\in \mathbb {N} \quad \Rightarrow \quad V(u_{k}-u,\Omega)\leq \liminf _{j\rightarrow +\infty }V(u_{k}-u_{j},\Omega)\leq \varepsilon }

\ Vert u_ {j} -u_ {k} \ Vert _ {{BV}} <\ varepsilon \ quad \ forall j, k \ geq N \ in {\ mathbb {N}} \ quad \ Rightarrow \ quad V (u_ {k} -u, \ Omega) \ leq \ liminf _ {{j \ rightarrow + \ infty}} V (u_ {k} -u_ {j}, \ Omega) \ leq \ varepsilon

Отсюда мы выводим, что $V ( ⋅, Ω) {\ displaystyle \ scriptstyle V (\ cdot, \ Omega)}$ $\ scriptstyle V (\ cdot, \ Omega)$ непрерывно, потому что это норма.

BV (Ω) неразделимо

Чтобы убедиться в этом, достаточно рассмотреть следующий пример, принадлежащий пространству $BV ([0, 1]) { \ displaystyle BV ([0,1])}$ $BV([0,1 ])$ : для каждого 0 < α < 1 define

χ α = χ [α, 1] = {0, если x ∉ [α, 1], 1, если x ∈ [α, 1] {\ displaystyle \ chi _ {\ alpha} = \ chi _ {[\ alpha, 1]} = {\ begin {cases} 0 {\ t_dv {if}} x \ notin \; [\ alpha, 1] \\ 1 {\ t_dv {if}} x \ in [\ alpha, 1] \ end {cases}}}

\ chi _ {\ alpha} = \ chi _ {{[\ alpha, 1]}} = {\ begin {cases} 0 {\ t_dv {if}} x \ notin \; [\ alpha, 1] \\ 1 {\ t_dv {if}} x \ in [\ alpha, 1] \ end {cases}}

как характеристическая функция замкнутого влево интервала $[α, 1] {\ displaystyle [\ alpha, 1]}$ $[\ alpha, 1]$ . Тогда, выбирая α, β∈ $[0, 1] {\ displaystyle [0,1]}$ $[0,1]$ так, чтобы α ≠ β, выполнялось следующее соотношение:

‖ χ α - χ β ‖ BV = 2 {\ displaystyle \ Vert \ chi _ {\ alpha} - \ chi _ {\ beta} \ Vert _ {BV} = 2}

{\ displaystyle \ Vert \ чи _ {\ альфа} - \ чи _ {\ бета} \ Vert _ {BV} = 2}

Теперь, чтобы доказать, что каждое плотное подмножество из $BV (] 0, 1 [) {\ displaystyle BV (] 0,1 [)}$ $BV (] 0,1 [)$ не может быть счетным, достаточно увидеть, что для каждого $α ∈ [0, 1] {\ displaystyle \ alpha \ in [0,1]}$ $\ alpha \ in [0,1]$ можно построить шары

B α = {ψ ∈ BV ( [0, 1]); ‖ Χ α - ψ ‖ BV ≤ 1} {\ Displaystyle B _ {\ alpha} = \ left \ {\ psi \ in BV ([0,1]); \ Vert \ chi _ {\ alpha} - \ psi \ Vert _ {BV} \ leq 1 \ right \}}

B _ {\ alpha} = \ left \ {\ psi \ in BV ([0,1]); \ Vert \ chi _ {\ alpha} - \ psi \ Vert _ {{BV}} \ leq 1 \ right \}

Очевидно, эти шары попарно не пересекаются, а также являются индексированным семейством из множеств, набор индексов равен $[0, 1] {\ displaystyle [0,1]}$ $[0,1]$ . Это означает, что это семейство имеет мощность континуума : теперь, поскольку каждое плотное подмножество $BV ([0, 1]) {\ displaystyle BV ([0,1])}$ $BV([0,1 ])$ должен иметь по крайней мере точку внутри каждого члена этого семейства, его мощность должна быть не менее мощности континуума и, следовательно, не может быть счетным подмножеством. Этот пример, очевидно, может быть расширен на более высокие измерения, и поскольку он включает только локальные свойства, это означает, что то же свойство верно и для $BV loc {\ displaystyle BV_ {loc}}$ $BV _ {{loc}}$ .

Цепное правило для функций BV

Цепное правило для негладких функций очень важно в математике и математической физике, так как есть несколько важных физические модели, поведение которых описывается функциями или функционалами с очень ограниченной степенью гладкости. Следующее цепное правило доказано в статье (Вольперт 1967, с. 248). Обратите внимание, что все частные производные должны интерпретироваться в обобщенном смысле, то есть как обобщенные производные.

Теорема . Пусть $f: R p → R {\ displaystyle \ scriptstyle f: \ mathbb {R} ^ {p} \ rightarrow \ mathbb {R}}$ $\ scriptstyle f: {\ mathbb {R}} ^ {p} \ rightarrow {\ mathbb {R}}$ будет функцией класса $C 1 {\ displaystyle C ^ {1}}$ $C ^ {1 }$ (т.е. непрерывная и дифференцируемая функция, имеющая непрерывную производные ) и пусть $u (x) = (u 1 (x),…, up (x)) {\ displaystyle \ scriptstyle {\ boldsymbol {u}} ({\ boldsymbol {x}}) = (u_ {1 } ({\ boldsymbol {x}}), \ ldots, u_ {p} ({\ boldsymbol {x}}))}$ $\ scriptstyle {\ boldsymbol {u}} ({\ boldsymbol {x}}) = (u_ {1} ({\ boldsymbol {x }}), \ ldots, u_ {p} ({\ boldsymbol {x}}))$ быть функцией в $BV (Ω) { \ displaystyle BV (\ Omega)}$ $BV (\ Omega)$ , где $Ω {\ displaystyle \ Omega}$ $\ Omega$ является открытым подмножеством из $R n {\ displaystyle \ scriptstyle \ mathbb {R} ^ {n}}$ $\ scriptstyle {\ mathbb {R}} ^ {n}$ . Then $f ∘ u ( x) = f ( u ( x)) ∈ B V ( Ω) {\displaystyle \scriptstyle f\circ {\boldsymbol {u}}({\boldsymbol {x}})=f({\boldsymbol {u}}({\boldsymbol {x}}))\in BV(\Omega)}$ $\ scriptstyle f \ circ {\ boldsymbol {u}} ({ \ boldsymbol {x}}) = е ({\ boldsymbol {u}} ({\ boldsymbol {x}})) \ in BV (\ Omega)$ and

∂ f ( u ( x)) ∂ x i = ∑ k = 1 p ∂ f ¯ ( u ( x)) ∂ u k ∂ u k ( x) ∂ x i ∀ i = 1, …, n {\displaystyle {\frac {\partial f({\boldsymbol {u}}({\boldsymbol {x}}))}{\partial x_{i}}}=\sum _{k=1}^{p}{\frac {\partial {\bar {f}}({\boldsymbol {u}}({\boldsymbol {x}}))}{\partial u_{k}}}{\frac {\partial {u_{k}({\boldsymbol {x}})}}{\partial x_{i}}}\qquad \forall i=1,\ldots,n}

{\ frac {\ partial f ({\ boldsymbol {u}} ({\ boldsymbol {x}}))} {\ partial x_ {i}}} = \ sum _ {{k = 1}} ^ {p} {\ frac {\ partial {\ bar {f}} ({\ boldsymbol {u}} ({ \ boldsymbol {x}}))} {\ partial u_ { k}}} {\ frac {\ partial {u_ {k} ({\ boldsymbol {x}})}} {\ partial x_ {i}}} \ qquad \ forall i = 1, \ ldots, n

where $f ¯ ( u ( x)) {\displaystyle \scriptstyle {\bar {f}}({\boldsymbol {u}}({\boldsymbol {x}}))}$ $\ scriptst yle {\ bar f} ({\ boldsymbol {u}} ({\ boldsymbol {x}}))$ is the mean value of the function at the point $x ∈ Ω {\displaystyle \scriptstyle x\in \Omega }$ $\ scriptstyle x \ в \ Omega$ , defined as

f ¯ ( u ( x)) = ∫ 0 1 f ( u a ^ ( x) t + u − a ^ ( x) ( 1 − t)) d t {\displaystyle {\bar {f}}({\boldsymbol {u}}({\boldsymbol {x}}))=\int _{0}^{1}f\left({\boldsymbol {u}}_{\boldsy mbol {\hat {a}}}({\boldsymbol {x}})t+{\boldsymbol {u}}_{-{\boldsymbol {\hat {a}}}}({\boldsymbol {x}})(1-t)\right)\,dt}

{\ displaystyle {\ bar {f}} ({\ boldsymbol {u}} ({\ boldsymbol {x}})) = \ int _ {0} ^ {1} f \ left ({\ boldsymbol {u}} _ {\ boldsymbol {\ hat {a}}} ({\ boldsymbol {x}}) t + {\ boldsymbol {u}} _ {- {\ boldsymbol {\ hat {a}} }} ({\ boldsymbol {x}}) (1-t) \ right) \, dt}

A more general chain rule formula for Lipschitz continuous functions $f : R p → R s {\displaystyle \scriptstyle f:\mathbb {R} ^{p}\rightarrow \mathbb {R} ^{s}}$ $\ scriptstyle f: {\ mathbb {R}} ^ {p} \ rightarrow {\ mathbb {R}} ^ {s}$ has been found by Luigi Ambrosio and Gianni Dal Maso and is published in the paper (Ambrosio Dal Maso 1990). However, even this formula has very important direct consequences: using $( u ( x), v ( x)) {\displaystyle (u({\boldsymbol {x}}),v({\boldsymbol {x}}))}$ ${\ displaystyle (u ({\ boldsymbol {x}}), v ({\ boldsymbol {x}}))}$ in place of $u ( x) {\displaystyle {\boldsymbol {u}}({\boldsymbol {x}})}$ ${\ displaystyle {\ boldsymbol {u}} ({\ boldsymbol {x}})}$ , where $v ( x) {\displaystyle v({\boldsymbol {x}})}$ ${\ displaystyle v ({\ boldsymbol {x}})}$ is also a $B V {\displaystyle BV}$ $BV$ function and choosing $f ( ( u, v)) = u v {\displaystyle f((u,v))=uv}$ ${\ displaystyle f ((u, v)) = uv}$ , the preceding formula gives the Leibniz rule for $B V {\displaystyle BV}$ $BV$ functions

∂ v ( x) u ( x) ∂ x i = u ¯ ( x) ∂ v ( x) ∂ x i + v ¯ ( x) ∂ u ( x) ∂ x i {\displaystyle {\frac {\partial v({\boldsymbol {x}})u({\boldsymbol {x}})}{\partial x_{i}}}={{\bar {u}}({\boldsymbol {x}})}{\frac {\partial v({\boldsymbol {x}})}{\partial x_{i}}}+{{\bar {v}}({\boldsymbol {x}})}{\frac {\partial u({\boldsymbol {x}})}{\partial x_{i}}}}

{\ frac {\ partial v ({\ boldsymbol {x}}) u ({\ boldsymbol {x}})} {\ partial x_ {i}}} = {{\ bar u} ({\ boldsymbol {x}})} {\ frac {\ partial v ({\ boldsymbol {x}})} {\ partial x_ {i}}} + {{\ bar v} ({\ boldsymbol {x} })} {\ frac {\ partial u ({\ boldsymbol {x}})} {\ partial x_ {i}}}

This implies that the product of two functions of bounded va riation is again a function of bounded variation, therefore $B V ( Ω) {\displaystyle BV(\Omega)}$ $BV (\ Omega)$ is an algebra.

BV(Ω) is a Banach algebra

This property follows directly from the fact that $B V ( Ω) {\displaystyle BV(\Omega)}$ $BV (\ Omega)$ is a Banach space and also an associative algebra : this implies that if ${ v n } {\displaystyle \{v_{n}\}}$ $\{v_{n}\}$ and ${ u n } {\displaystyle \{u_{n}\}}$ $\ {u_n \}$ are Cauchy sequences of $B V {\displaystyle BV}$ $BV$ functions converging respectively to functions $v {\displaystyle v}$ $v$ and $u {\displaystyle u}$ $u$ in $B V ( Ω) {\displaystyle BV(\Omega)}$ $BV (\ Omega)$ , then

v u n → n → ∞ v u v n u → n → ∞ v u ⟺ v u ∈ B V ( Ω) {\displaystyle {\begin{matrix}vu_{n}{\xrightarrow[{n\to \infty }]{}}vu\\v_{n}u{\xrightarrow[{n\to \infty }]{}}vu\end{matrix}}\quad \Longleftrightarrow \quad vu\in BV(\Omega)}

{\ begin {matrix} vu_ {n} {\ xrightarrow [{n \ to \ infty }] {}} vu \\ v_ {n} u {\ xrightarrow [{n \ to \ infty}] {}} vu \ end {matrix}} \ quad \ Longleftrightarrow \ quad vu \ in BV (\ Omega)

therefore the ordinary produ ct of functions is continuous in $B V ( Ω) {\displaystyle BV(\Omega)}$ $BV (\ Omega)$ with respect to each argument, making this function space a Banach algebra.

Generalizations and extensions

Weighted BV functions

It is possible to generalize the above notion of total variation so that different variations are weighted differently. More precisely, let $φ : [ 0, + ∞) ⟶ [ 0, + ∞) {\displaystyle \scriptstyle \varphi :[0,+\infty)\longrightarrow [0,+\infty)}$ $\ scriptstyle \ varphi: [0, + \ infty) \ longrightarrow [0, + \ infty)$ be any increasing function such that $φ ( 0) = φ ( 0 +) = lim x → 0 + φ ( x) = 0 {\displaystyle \scriptstyle \varphi (0)=\varphi (0+)=\lim _{x\rightarrow 0_{+}}\varphi (x)=0}$ $\ scriptstyle \ varphi (0) = \ varphi (0 +) = \ lim _ {{x \ rightarrow 0 _ {+ }}} \ varphi (x) = 0$ (the weight function ) and let $f : [ 0, T ] ⟶ X {\displaystyle \scriptstyle f:[0,T]\longrightarrow X}$ $\ scriptstyle f: [ 0, T] \ longrightarrow X$ be a function from the interval $[ 0, T ] {\displaystyle [0,T]}$ $[0, T]$ ⊂ℝ taking values in a normed vector space $X {\displaystyle X}$ $X$ . Then the $φ {\displaystyle \scriptstyle {\boldsymbol {\varphi }}}$ $\ scriptstyle {\ boldsymbol \ varphi}$ -variationof $f {\displaystyle f}$ $f$ over $[ 0, T ] {\displaystyle [0,T]}$ $[0, T]$ is defined as

φ - Var [ 0, T ] ⁡ ( f) := sup ∑ j = 0 k φ ( | f ( t j + 1) − f ( t j) | X), {\ displaystyle \ mathop {\ varphi {\ text {-}} \ operatorname {Var}} _ {[0, T]} (f): = \ sup \ sum _ {j = 0} ^ {k} \ varphi \ left (| f (t_ {j + 1}) - f (t_ {j}) | _ {X} \ right),}

{\ displaystyle \ mathop {\ varphi {\ text {-}} \ operatorname {Var}} _ {[0, T]} (f): = \ sup \ sum _ {j = 0} ^ {k} \ varphi \ left (| е (t_ {j + 1}) - f (t_ {j}) | _ {X} \ right),}

где, как обычно, супремум берется по всем конечным разделы интервала $[0, T] {\ displaystyle [0, T]}$ $[0, T]$ , т.е. все конечные наборы из действительных чисел $ti {\ displaystyle t_ {i}}$ $t_ {i}$ так, что

0 = t 0 < t 1 < ⋯ < t k = T. {\displaystyle 0=t_{0}

{\ displaystyle 0 = t_ {0 } <t_ {1} <\ cdots <t_{k}=T.}

Исходное понятие варианта, рассмотренное выше, является частным случаем $φ {\ displaystyle \ scriptstyle \ varphi}$ $\ scriptstyle \ varphi$ - вариация, для которой весовой функцией является функция идентичности : следовательно, интегрируемая функция $f { \ displaystyle f}$ $f$ называется взвешенной функцией BV (с весом $φ {\ displaystyle \ scriptstyle \ varphi}$ $\ scriptstyle \ varphi$ ) тогда и только тогда, когда его $φ {\ displaystyle \ scriptstyle \ varphi}$ $\ scriptstyle \ varphi$ -вариация конечна.

f ∈ BV φ ([0, T]; X) ⟺ φ - Var [0, T] ⁡ (f) < + ∞ {\displaystyle f\in BV_{\varphi }([0,T];X)\iff \mathop {\varphi {\text{-}}\operatorname {Var} } _{[0,T]}(f)<+\infty }

{\ displaystyle f \ in BV _ {\ varphi } ([0, T]; X) \ iff \ mathop {\ varphi {\ text {-}} \ operatorname {Var}} _ {[0, T]} (f) <+ \ infty}

Пространство $BV φ ([0, T]; X) {\ displaystyle \ scriptstyle BV _ {\ varphi} ([0, T]; X)}$ $\ scriptstyle BV _ {\ varp привет} ([0, T]; X)$ - это топологическое векторное пространство относительно нормы нормы

‖ f ‖ BV φ: знак равно ‖ е ‖ ∞ + φ - Var [0, T] ⁡ (f), {\ displaystyle \ | f \ | _ {BV _ {\ varphi}}: = \ | f \ | _ {\ infty} + \ mathop {\ varphi {\ text {-}} \ operatorname {Var}} _ {[0, T]} (f),}

{\ displaystyle \ | f \ | _ {BV _ {\ varphi}}: = \ | f \ | _ {\ infty} + \ mathop {\ varphi {\ text {-}} \ operatorname {Var}} _ {[0, T]} (f),}

где $‖ f ‖ ∞ {\ displaystyle \ scriptstyle \ | f \ | _ {\ infty}}$ $\ scriptstyle \ | е \ | _ {{\ infty}}$ обозначает обычную норму супремума для $f {\ displaystyle f}$ $f$ . Взвешенные BV-функции были введены и изучены в полной мере Владиславом Орличем и в статье Musielak Orlicz 1959 : Лоуренс Чисхолм Янг ранее изучал случай $φ (x) = xp {\ displaystyle \ scriptstyle \ varphi (x) = x ^ {p}}$ $\ scriptstyle \ varphi (x) = x ^ {p}$ , где $p {\ displaystyle p}$ $p$ - положительное целое число.

Функции SBV

Функции SBV т.е. Специальные функции ограниченной вариации были введены Луиджи Амбросио и Эннио де Джорджи в статье (Ambrosio De Giorgi 1988), посвященной свободной прерывности вариационные задачи : задано открытое подмножество $Ω {\ displaystyle \ Omega}$ $\ Omega$ из ℝ, пространство $SBV (Ω) {\ displaystyle SBV (\ Omega)}$ $SBV (\ Omega)$ является правильным линейным подпространством в $BV (Ω) {\ displaystyle BV (\ Omega)}$ $BV (\ Omega)$ , поскольку weak градиент каждой принадлежащей ему функции состоит в точности из суммы $n {\ displaystyle n}$ $n$ -размерной опоры и $n - 1 {\ displaystyle n-1}$ $n-1$ -мерная поддержка мера без промежуточных терминов, как показано в следующем определении.

Определение . Для локально интегрируемой функции $u {\ displaystyle u}$ $u$ , тогда $u ∈ SBV (Ω) {\ displaystyle \ scriptstyle u \ in {S \! BV} (\ Omega)}$ $\ scriptstyle u \ in {S \! BV} (\ Omega)$ тогда и только тогда, когда

1.существуют две функции Бореля $f {\ displaystyle f}$ $f$ и $g {\ displaystyle g}$ $g$ из домена $Ω {\ displaystyle \ Omega}$ $\ Omega$ и codomain ℝ такие, что

∫ Ω | f | d H n + ∫ Ω | г | d H n - 1 < + ∞. {\displaystyle \int _{\Omega }\vert f\vert \,dH^{n}+\int _{\Omega }\vert g\vert \,dH^{n-1}<+\infty.}

{\ displaystyle \ int _ {\ Omega} \ vert f \ vert \, dH ^ {n} + \ int _ {\ Omega} \ vert g \ vert \, dH ^ {n-1} <+ \ infty.}

2.Для всех непрерывно дифференцируемых векторных функций $ϕ {\ displaystyle \ scriptstyle \ phi}$ $\ scriptstyle \ phi$ of compact поддержка содержится в $Ω {\ displaystyle \ Omega}$ $\ Omega$ , т.е. для всех $ϕ ∈ C c 1 (Ω, R n) {\ displaystyle \ scriptstyle \ phi \ in C_ {c} ^ {1} (\ Omega, \ mathbb {R} ^ {n})}$ $\ scriptstyle \ phi \ in C_ {c} ^ {1} (\ Omega, {\ mathbb {R}} ^ {n})$ верна следующая формула:

∫ Ω u div ⁡ ϕ d H n = ∫ Ω ⟨ ϕ, f d H n + Ω ⟨ϕ, g⟩ d H n - 1. {\ displaystyle \ int _ {\ Omega} u \ operatorname {div} \ phi \, dH ^ {n} = \ int _ {\ Omega} \ langle \ phi, f \ rangle \, dH ^ {n} + \ int _ {\ Omega} \ langle \ phi, g \ rangle \, dH ^ {n-1}.}

{\ displaystyle \ int _ {\ Omega} u \ operatorname {div} \ phi \, dH ^ {n} = \ int _ {\ Omega} \ langle \ phi, f \ rangle \, dH ^ {n} + \ int _ {\ Омега} \ langle \ phi, g \ rangle \, dH ^ {n-1}.}

где $H α {\ displaystyle H ^ {\ alpha}}$ $H ^ {\ alpha}$ является $α {\ displaystyle \ alpha}$ $\ alpha$ -мерной мерой Хаусдорфа.

Подробные сведения о свойствах функций SBV можно найти в работах, цитируемых в разделе библиографии: в частности, в статье (De Giorgi 1992) содержит полезную библиографию.

bv последовательностей

В качестве конкретных примеров банаховых пространств, Dunford Schwartz (1958, Глава IV) harvtxt error: no target: CITEREFDunfordSchwartz1958 (help ) рассмотреть пространства последовательностей ограниченной вариации в дополнение к пространствам функций ограниченной вариации. Полная вариация последовательности x = (x i) действительных или комплексных чисел определяется как

T V (x) = ∑ i = 1 ∞ | х я + 1 - х я |. {\ displaystyle TV (x) = \ sum _ {i = 1} ^ {\ infty} | x_ {i + 1} -x_ {i} |.}

TV (x) = \ sum _ {{i = 1}} ^ {\ infty} | x _ {{i + 1}} - x_ {i} |.

Обозначается пространство всех последовательностей конечной полной вариации пользователя bv. Норма на bv определяется как

‖ x ‖ b v = | х 1 | + TV ⁡ (x) = | х 1 | + ∑ i = 1 ∞ | х я + 1 - х я |. {\ displaystyle \ | x \ | _ {bv} = | x_ {1} | + \ operatorname {TV} (x) = | x_ {1} | + \ sum _ {i = 1} ^ {\ infty} | x_ {i + 1} -x_ {i} |.}

{\ displaystyle \ | x \ | _ {bv} = | x_ {1} | + \ operatorname {TV} (x) = | x_ {1} | + \ sum _ {i = 1} ^ {\ infty} | x_ {i + 1} -x_ {i} |.}

С этой нормой пространство bv является банаховым, которое изоморфно $ℓ 1 {\ displaystyle \ ell _ {1}}$ $\ ell _ {1}$ .

Сама полная вариация определяет норму на некотором подпространстве bv, обозначаемом bv 0, состоящем из последовательностей x = (x i), для которых

lim n → ∞ xn = 0. {\ displaystyle \ lim _ {n \ to \ infty} x_ {n} = 0.}

\ lim _ {{n \ to \ infty}} x_ {n} = 0.

Норма на bv 0 обозначается

‖ x ‖ bv 0 = TV (x) = ∑ i = 1 ∞ | х я + 1 - х я |. {\ displaystyle \ | x \ | _ {bv_ {0}} = TV (x) = \ sum _ {i = 1} ^ {\ infty} | x_ {i + 1} -x_ {i} |.}

\ | x \ | _ {{bv_ {0}}} = TV (x) = \ sum _ {{i = 1}} ^ {\ infty} | x _ {{i + 1}} - x_ {i} |.

В отношении этой нормы bv 0 также становится банаховым пространством, которое изоморфно и изометрично $ℓ 1 {\ displaystyle \ ell _ {1}}$ $\ ell _ {1}$ ( хотя и не естественным путем).

Меры ограниченной вариации

A со знаком (или сложным ) мера $μ {\ displaystyle \ mu}$ $\ mu$ на измеримом пространстве $(X, Σ) {\ displaystyle (X, \ Sigma)}$ $(X, \ Sigma)$ называется ограниченной вариацией, если его общая вариация $‖ μ ‖ = | μ | (X) {\ displaystyle \ scriptstyle \ Vert \ mu \ Vert = | \ mu | (X)}$ $\ scriptstyle \ Vert \ mu \ Vert = | \ mu | (X)$ ограничен: см. Halmos (1950, p. 123), Колмогоров и Фомин (1969, стр. 346) или запись «Полная вариация » для получения дополнительных сведений.

Примеры

Функция f (x) = sin (1 / x) не имеет ограниченной вариации на интервале

[0, 2 / π] {\ displaystyle [0,2 / \ pi]}

[0,2 / \ pi]

Функция

f (x) = {0, если x = 0 sin ⁡ (1 / x), если x ≠ 0 {\ displaystyle f (x) = {\ begin {cases} 0, {\ t_dv {if}} x = 0 \\\ sin (1 / x), {\ t_dv {if}} x \ neq 0 \ end {cases}}}

f (x) = {\ begin {cases} 0, {\ mb ox {if}} x = 0 \\\ sin (1 / x), {\ t_dv {if}} x \ neq 0 \ end {cases}}

не имеет ограниченной вариации на интервал $[0, 2 / π] {\ displaystyle [0,2 / \ pi]}$ $[0,2 / \ pi]$

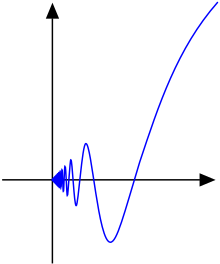
Функция f (x) = x sin (1 / x) не имеет ограниченного изменения на интервале

[0, 2 / π] {\ displaystyle [0,2 / \ pi]}

[0,2 / \ pi]

Хотя это сложнее увидеть, непрерывная функция

f (x) = {0, если x = 0 x грех ⁡ (1 / x), если x ≠ 0 {\ displaystyle f (x) = {\ begin {cases} 0, {\ t_dv {if}} x = 0 \\ x \ sin (1 / x), {\ t_dv {if}} x \ neq 0 \ end {cases}}}

f (x) = \ begin {cases} 0, \ t_dv {if} x = 0 \\ x \ sin (1 / x), \ t_dv {if} x \ neq 0 \ end {case}

не имеет ограниченной вариации на интервале $[0, 2 / π] {\ displaystyle [0,2 / \ pi ]}$ $[0,2 / \ pi]$ либо.

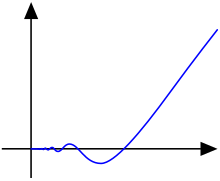
Функция f (x) = x sin (1 / x) имеет ограниченную вариацию на интервале

[0, 2 / π] {\ displaystyle [0,2 / \ pi]}

[0,2 / \ pi]

При в то же время функция

f (x) = {0, если x = 0 x 2 sin ⁡ (1 / x), если x ≠ 0 {\ displaystyle f (x) = {\ begin {cases} 0, {\ t_dv {if}} x = 0 \\ x ^ {2} \ sin (1 / x), {\ t_dv {if}} x \ neq 0 \ end {cases}}}

f (x) = {\ begin {cases} 0, {\ t_dv {if}} x = 0 \\ x ^ {2} \ sin (1 / x), {\ t_dv {if}} x \ neq 0 \ end {cases}}

равно ограниченной вариации на интервале $[0, 2 / π] {\ displaystyle [0,2 / \ pi]}$ $[0,2 / \ pi]$ . Однако все три функции имеют ограниченную вариацию на каждом интервале $[a, b] {\ displaystyle [a, b]}$ $[a, b]$ с $a>0 {\ displaystyle a>0}$ $a>0$ .

Пространство Соболева $W 1, 1 (Ω) {\ displaystyle W ^ {1,1} (\ Omega)}$ $W ^ {{1,1}} (\ Omega)$ является правильным подмножеством из $BV (Ω) {\ displaystyle BV (\ Omega)}$ $BV (\ Omega)$ . Фактически, для каждого $u {\ displaystyle u}$ $u$ в $W 1, 1 (Ω) {\ displaystyle W ^ {1,1} (\ Omega)}$ $W ^ {{1,1}} (\ Omega)$ можно выбрать меру $μ: = ∇ u L {\ displaystyle \ scriptstyle \ mu: = \ nabla u {\ mathcal {L}}}$ $\ scriptstyle \ mu: = \ nabla u {\ mathcal L}$ (где $L {\ displaystyle \ scriptstyle {\ mathcal {L}}}$ $\ scriptstyle {\ mathcal L}$ - это мера Лебега на $Ω {\ displaystyle \ Omega}$ $\ Omega$ ) такая, что

∫ u div ⁡ ϕ = - ∫ ϕ d μ = - ∫ ϕ ∇ u ∀ ϕ ∈ С с 1 {\ Displaystyle \ Int U \ OperatorName {Div} \ phi = - \ int \ phi \, d \ mu = - \ int \ phi \, \ nabla u \ qquad \ forall \ phi \ in C_ {c} ^ {1}}

{ \ Displaystyle \ int и \ OperatorName {div} \ phi = - \ int \ phi \, d \ mu = - \ int \ phi \, \ nabla и \ qquad \ forall \ phi \ in C_ {c} ^ {1} }

, поскольку это не что иное, как определение слабой производной и, следовательно, верно. Можно легко найти пример функции BV, которая не является $W 1, 1 {\ displaystyle W ^ {1,1}}$ $W ^ {{1,1}}$ : в первом измерении любая ступенчатая функция с нетривиальным прыжок сделаю.

Приложения

Математика

Функции ограниченной вариации изучались в связи с множеством разрывов функций и дифференцируемости вещественных функций, а также следующие результаты хорошо известны. Если $f {\ displaystyle f}$ $f$ - это real функция ограниченной вариации на интервале $[a, b] {\ displaystyle [ a, b]}$ $[a, b]$ , тогда

$f {\ displaystyle f}$ $f$ является непрерывным, кроме не более чем на счетном множестве ;
$f { \ displaystyle f}$ $f$ имеет односторонние ограничения везде (пределы слева везде в $(a, b] {\ displaystyle (a, b]}$ $(a, b]$ и всюду справа в $[a, b) {\ displaystyle [a, b)}$ $[a, b)$ ;
производное $f ′ (x) {\ displaystyle f ' (x)}$ $f'(x)$ существует почти везде (т. е. кроме набора нулевой меры ).

Для вещественных функций из несколько вещественных переменных

характеристическая функция набора Каччопполи является функцией BV: BV-функции лежат в основе современной теории периметров.
Минимальные поверхности - это графики функций BV: в этом контексте см. ссылку (Giusti 1984).

Physics and Engine ering

Способность функций BV работать с разрывами широко использовалась в прикладных науках: решения задач механики, физики, химической кинетики очень часто можно представить функциями ограниченной вариации. В книге (Худжаев и Вольперт 1985) подробно описан очень обширный набор приложений BV-функций в математической физике. Также есть несколько современных приложений, которые заслуживают краткого описания.

Функционал Мамфорда – Шаха : проблема сегментации для двумерного изображения, т.е. проблема точного воспроизведения контуров и серых шкал, эквивалентна минимизации таких функциональная.
Полная вариация шумоподавления

См. Также

Примечания

Литература

Внешние ссылки

Теория

Голубов, Борис I.; Витушкин, Анатолий Г. (2001) [1994], Математическая энциклопедия, EMS Press
«Функция BV». PlanetMath..
Роуленд, Тодд и Вайсштейн, Эрик У. «Ограниченная вариация». MathWorld. CS1 maint: несколько имен: список авторов (ссылка )
Функция ограниченной вариации в Энциклопедия математики

Другое

Луиджи Амброзио домашняя страница в Scuola Normale Superiore di Pisa. Академическая домашняя страница (с препринтами и публикациями) одного из авторов теории и приложений BV-функций.
Исследовательская группа in Calculus of Variations and Geometric Measure Theory, Scuola Normale Superiore di Pisa.

. В этой статье используется материал из функции BV по PlanetMath, которая находится под лицензией Creative Commons Attribution / Share-Alike License.