Градиент

Многопараметрическое обобщение производной функции Градиент, представленный синими стрелками, обозначает направление наибольшего изменения скалярной функции. Значения функции представлены в оттенках серого и увеличиваются по значению от белого (низкий) до темного (высокий).

В векторном исчислении , градиент из скалярная дифференцируемая функция f нескольких переменных - это векторное поле (или векторная функция ) $\nabla \; f\; \{\backslash \; displaystyle\; \backslash \; nabla\; f\}$, значением которого в точке $p\; \{\backslash \; displaystyle\; p\}$является вектор, компонентами которого являются частные производные от $f\; \{\backslash \; displaystyle\; f\}$в $p\; \{\backslash \; displaystyle\; p\}$. То есть для $f:\; R\; n\; \to \; R\; \{\backslash \; displaystyle\; f\; \backslash \; двоеточие\; \backslash \; mathbf\; \{R\}\; ^\; \{n\}\; \backslash \; to\; \backslash \; mathbf\; \{R\}\}$его градиент $\nabla \; f\; :\; R\; n\; \to \; R\; n\; \{\backslash \; displaystyle\; \backslash \; nabla\; f\; \backslash \; двоеточие\; \backslash \; mathbf\; \{R\}\; ^\; \{n\}\; \backslash \; to\; \backslash \; mathbf\; \{R\}\; ^\; \{n\}\}$определено в точке $p\; =\; (x\; 1,\dots ,\; xn)\; \{\backslash \; displaystyle\; \backslash \; mathrm\; \{p\}\; =\; (x\_\; \{1\},\; \backslash \; ldots,\; x\_\; \{n\})\}$в n-мерном пространстве как вектор:

$\nabla \; f\; (p)\; =\; [\partial \; f\; \partial \; x\; 1\; (p)\; ⋮\; \partial \; f\; \partial \; xn\; (p)].\; \{\backslash \; displaystyle\; \backslash \; nabla\; f\; (p)\; =\; \{\backslash \; begin\; \{bmatrix\}\; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; x\_\; \{1\}\}\}\; (p)\; \backslash \backslash \backslash \; vdots\; \backslash \backslash \; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; x\_\; \{n\}\}\}\; (p)\; \backslash \; end\; \{bmatrix\}\}.\}$

Символ набла $\nabla \; \{\backslash \; displaystyle\; \backslash \; nabla\}$, написано в виде перевернутого треугольника и произносится как «дель», обозначает векторный дифференциальный оператор.

Градиент двойственен производному $df\; \{\backslash \; displaystyle\; df\}$: значение градиента в точке - это касательный вектор - вектор в каждой точке; в то время как значение производной в точке является вектором котангенса - линейной функцией на векторах. Они связаны тем, что скалярное произведение градиента f в точке p с другим касательным вектором v равно производной по направлению f в точке p функция по v ; то есть $\nabla \; е\; (п)\; \cdot \; v\; =\; \partial \; е\; \partial \; v\; (p)\; =\; dfp\; (v)\; \{\backslash \; displaystyle\; \backslash \; nabla\; f\; (p)\; \backslash \; cdot\; \backslash \; mathrm\; \{v\}\; =\; \{\backslash \; tfrac\; \{\backslash \; partial\; f\; \}\; \{\backslash \; partial\; \backslash \; mathbf\; \{v\}\}\}\; (p)\; =\; df\_\; \{p\}\; (\backslash \; mathrm\; \{v\})\}$.

Вектор градиента можно интерпретировать как «направление и скорость наиболее быстрого увеличения». Если градиент функции не равен нулю в точке p, направление градиента - это направление, в котором функция увеличивается наиболее быстро от p, а величина градиента - это скорость увеличения. в этом направлении. Кроме того, градиент является нулевым вектором в точке тогда и только тогда, когда это неподвижная точка (где производная обращается в нуль). Таким образом, градиент играет фундаментальную роль в теории оптимизации, где он используется для максимизации функции с помощью подъема градиента.

Градиент допускает множественные обобщения для более общих функций на многообразиях ; см. § Обобщения.

• 1 Мотивация
• 2 Определение
  • 2.1 Декартовы координаты
  • 2.2 Цилиндрические и сферические координаты
  • 2.3 Общие координаты
• 3 Градиент и производная или дифференциал
  • 3.1 Дифференциальная или (внешняя) производная
  • 3.2 Линейное приближение к функции
  • 3.3 Градиент как «производная»
    • 3.3.1 Линейность
    • 3.3.2 Правило произведения
    • 3.3.3 Цепное правило
• 4 Другие свойства и приложения
  • 4.1 Наборы уровней
  • 4.2 Консервативные векторные поля и градиентная теорема
• 5 Обобщения
  • 5.1 Градиент вектора
  • 5.2 Римановы многообразия
• 6 См. Также
• 7 Примечания
• 8 Ссылки
• 9 Дополнительная литература
• 10 Внешние ссылки

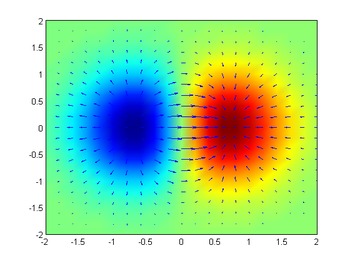Градиент 2D-функции f (x, y) = xe показан синими стрелками над псевдоцветной график функции.

Рассмотрим комнату, где температура задается скалярным полем , T, поэтому в каждой точке (x, y, z) температура равна T (x, y, z), независимо от времени. В каждой точке комнаты градиент T в этой точке покажет направление, в котором температура растет быстрее всего, удаляясь от (x, y, z). Величина градиента будет определять, насколько быстро температура повышается в этом направлении.

Рассмотрим поверхность, высота которой над уровнем моря в точке (x, y) равна H (x, y). Градиент H в точке - это вектор плоскости, указывающий в направлении наискорейшего склона или уклона в этой точке. Крутизна наклона в этой точке определяется величиной вектора градиента.

Градиент также можно использовать для измерения того, как скалярное поле изменяется в других направлениях, а не только в направлении наибольшего изменения, путем взятия скалярного произведения. Предположим, что самый крутой уклон холма составляет 40%. Дорога, идущая прямо в гору, имеет уклон 40%, но дорога, огибающая холм под углом, будет иметь более пологий уклон. Например, если дорога находится под углом 60 ° к направлению подъема (когда оба направления проецируются на горизонтальную плоскость), то уклон вдоль дороги будет скалярным произведением между вектором градиента и единичным вектором . вдоль дороги, а именно 40%, умноженное на косинус 60 °, или 20%.

В более общем смысле, если функция высоты холма H является дифференцируемой, то градиент H , пунктирный с единичным вектором дает наклон холм в направлении вектора, производная по направлению H вдоль единичного вектора.

Градиент функции f (x, y) = - (cosx + cosy), изображенный как спроецированное векторное поле на нижнюю плоскость.

Градиент (или градиентное векторное поле) скалярной функции f (x 1, x 2, x 3,..., x n) обозначается ∇f или ∇ → f, где ∇ (nabla ) обозначает вектор дифференциальный оператор, del. Обозначение grad f также обычно используется для представления градиента. Градиент f определяется как уникальное векторное поле, скалярное произведение которого с любым вектором vв каждой точке x является производной f по направлению вдоль v . То есть

$(\nabla \; f\; (x))\; \cdot \; v\; =\; D\; v\; f\; (x).\; \{\backslash \; displaystyle\; \{\backslash \; big\; (\}\; \backslash \; nabla\; f\; (x)\; \{\backslash \; big)\}\; \backslash \; cdot\; \backslash \; mathbf\; \{v\}\; =\; D\; \_\; \{\backslash \; mathbf\; \{v\}\}\; f\; (x).\}$

Формально градиент двойной к производной; см. связь с производной.

Когда функция также зависит от параметра, такого как время, градиент часто относится только к вектору ее пространственных производных (см. Пространственный градиент ).

Величина и направление вектора градиента независимы от конкретного представления координат .

декартовых координат

в трехмерном декартовом система координат с евклидовой метрикой, градиент, если он существует, задается следующим образом:

$\nabla \; f\; =\; \partial \; f\; \partial \; xi\; +\; \partial \; f\; \partial \; yj\; +\; \partial \; f\; \partial \; zk,\; \{\backslash \; displaystyle\; \backslash \; nabla\; f\; =\; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; x\}\}\; \backslash \; mathbf\; \{i\}\; +\; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; y\}\}\; \backslash \; mathbf\; \{j\}\; +\; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; z\}\}\; \backslash \; mathbf\; \{k\},\}$

где i, j, k- стандартные единичные векторы в направлениях координат x, y и z, соответственно. Например, градиент функции

$f\; (x,\; y,\; z)\; =\; 2\; x\; +\; 3\; y\; 2\; -\; sin\; \; (z)\; \{\backslash \; displaystyle\; f\; (x,\; y,\; z)\; =\; 2x\; +\; 3y\; ^\; \{2\; \}\; -\; \backslash \; sin\; (z)\}$

равно

$\nabla \; f\; =\; 2\; i\; +\; 6\; yj\; -\; cos\; \; (z)\; k.\; \{\backslash \; displaystyle\; \backslash \; nabla\; f\; =\; 2\; \backslash \; mathbf\; \{i\}\; +\; 6y\; \backslash \; mathbf\; \{j\}\; -\; \backslash \; cos\; (z)\; \backslash \; mathbf\; \{k\}.\}$

В некоторых приложениях принято представлять градиент как вектор-строка или вектор-столбец его компонентов в прямоугольной системе координат; в этой статье принято, что градиент является вектором-столбцом, а производная - вектором-строкой.

Цилиндрические и сферические координаты

В цилиндрических координатах с евклидовой метрикой градиент задается следующим образом:

$\nabla \; f\; (\rho ,\; \phi ,\; z)\; =\; \partial \; е\; \partial \; \rho \; е\; \rho \; +\; 1\; \rho \; \partial \; е\; \partial \; \phi \; е\; \phi \; +\; \partial \; е\; \partial \; zez,\; \{\backslash \; displaystyle\; \backslash \; nabla\; f\; (\backslash \; rho,\; \backslash \; varphi,\; z)\; =\; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; \backslash \; rho\}\; \}\; \backslash \; mathbf\; \{e\}\; \_\; \{\backslash \; rho\}\; +\; \{\backslash \; frac\; \{1\}\; \{\backslash \; rho\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; \backslash \; varphi\}\}\; \backslash \; mathbf\; \{e\}\; \_\; \{\backslash \; varphi\}\; +\; \{\; \backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; z\}\}\; \backslash \; mathbf\; \{e\}\; \_\; \{z\},\}$

где ρ - осевое расстояние, φ - азимутальный или азимутальный угол, z - осевая координата, а eρ, eφи ez- это единичные векторы, указывающие вдоль координатных направлений.

В сферических координатах градиент определяется следующим образом:

$\nabla \; f\; (r,\; \theta ,\; \phi )\; =\; \partial \; f\; \partial \; rer\; +\; 1\; r\; \partial \; f\; \partial \; \theta \; e\; \theta \; +\; 1\; р\; грех\; \; \theta \; \partial \; е\; \partial \; \phi \; е\; \phi ,\; \{\backslash \; displaystyle\; \backslash \; nabla\; f\; (r,\; \backslash \; theta,\; \backslash \; varphi)\; =\; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; r\}\}\; \backslash \; mathbf\; \{e\}\; \_\; \{r\}\; +\; \{\backslash \; frac\; \{1\}\; \{r\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; \backslash \; theta\}\}\; \backslash \; mathbf\; \{e\}\; \_\; \{\backslash \; theta\}\; +\; \{\backslash \; frac\; \{1\}\; \{r\; \backslash \; sin\; \backslash \; theta\}\; \}\; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; \backslash \; varphi\}\}\; \backslash \; mathbf\; \{e\}\; \_\; \{\backslash \; varphi\},\}$

где r - радиальное расстояние, φ - азимутальный угол, а θ - полярный угол, и er, eθи eφснова являются локальными единичными векторами, указывающими в направлениях координат (то есть нормализованным ковариантным базисом ).

Для градиента в других ортогональных системах координат см. Ортогональные координаты (Дифференциальные операторы в трех измерениях).

Общие координаты

Мы рассматриваем общие координаты, которые мы записываем как x,..., x,..., x, где n - количество измерений области. Здесь верхний индекс относится к позиции в списке координаты или компонента, поэтому x относится ко второму компоненту, а не к величине x в квадрате. Индексная переменная i относится к произвольному элементу x. Используя нотацию Эйнштейна, градиент может быть записан как:

$\nabla \; f\; =\; \partial \; f\; \partial \; xigijej\; \{\backslash \; displaystyle\; \backslash \; nabla\; f\; =\; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; x\; ^\; \{i\; \}\}\}\; g\; ^\; \{ij\}\; \backslash \; mathbf\; \{e\}\; \_\; \{j\}\}$(Обратите внимание, что его дуальный равен $df\; =\; \partial \; f\; \partial \; xiei\; \{\backslash \; displaystyle\; \backslash \; mathrm\; \{d\}\; f\; =\; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; x\; ^\; \{i\}\}\}\; \backslash \; mathbf\; \{e\}\; ^\; \{i\}\}$),

где $ei\; =\; \partial \; x\; /\; \partial \; xi\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{e\}\; \_\; \{i\}\; =\; \backslash \; partial\; \backslash \; mathbf\; \{x\}\; /\; \backslash \; partial\; x\; ^\; \{i\}\}$и $ei\; =\; dxi\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{e\}\; ^\; \{i\; \}\; =\; \backslash \; mathrm\; \{d\}\; x\; ^\; \{i\}\}$относятся к ненормализованным локальным ковариантным и контравариантным основаниям соответственно, $gij\; \{\backslash \; displaystyle\; g\; ^\; \{ij\}\}$- это обратный метрический тензор , а соглашение Эйнштейна о суммировании подразумевает суммирование по i и j.

Если координаты ортогональны, мы можем легко выразить градиент (и дифференциал ) в терминах нормализованных базисов, которые мы называем $e\; ^\; i\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; mathbf\; \{e\}\}\}\; \_\; \{i\}\}$и $e\; ^\; i\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; mathbf\; \{e\}\}\}\; ^\; \{i\}\}$, используя масштабные коэффициенты (также известные как коэффициенты Ламе ) $привет\; =\; \Vert \; ei\; \Vert \; =\; 1\; /\; \Vert \; ei\; \Vert \; \{\backslash \; displaystyle\; h\_\; \{i\}\; =\; \backslash \; lVert\; \backslash \; mathbf\; \{e\}\; \_\; \{i\}\; \backslash \; rVert\; =\; 1\; \backslash ,\; /\; \backslash \; lVert\; \backslash \; mathbf\; \{e\}\; ^\; \{я\}\; \backslash ,\; \backslash \; rVert\}$:

$\nabla \; е\; =\; \sum \; я\; =\; 1\; n\; \partial \; е\; \partial \; xi\; 1\; hie\; ^\; i\; \{\backslash \; displaystyle\; \backslash \; nabla\; f\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; \backslash ,\; \{\; \backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; x\; ^\; \{i\}\}\}\; \{\backslash \; frac\; \{1\}\; \{h\_\; \{i\}\}\}\; \backslash \; mathbf\; \{\backslash \; hat\; \{e\}\}\; \_\; \{i\}\}$(и $df\; =\; \sum \; я\; =\; 1\; N\; \partial \; е\; \partial \; xi\; 1\; hie\; ^\; i\; \{\backslash \; displaystyle\; \backslash \; mathrm\; \{d\}\; f\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; \backslash ,\; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; x\; ^\; \{i\}\}\}\; \{\backslash \; frac\; \{1\}\; \{h\_\; \{i\}\}\}\; \backslash \; mathbf\; \{\backslash \; hat\; \{e\}\}\; ^\; \{i\}\}$),

где мы не можем использовать нотацию Эйнштейна, поскольку невозможно избежать повторения более двух показателей. Несмотря на использование верхних и нижних индексов, $e\; ^\; i\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; hat\; \{e\}\}\; \_\; \{i\}\}$, $e\; ^\; i\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; hat\; \{e\}\}\; ^\; \{i\}\}$и $hi\; \{\backslash \; displaystyle\; h\_\; \{i\}\}$не являются ни контравариантными, ни ковариантными.

Последнее выражение вычисляет выражения, приведенные выше для цилиндрических и сферических координат.

Градиент тесно связан с (общей) производной ((общей) разностью ) $df\; \{\backslash \; displaystyle\; df\}$: они транспонируют (dual ) друг в друга. Используя соглашение, согласно которому векторы в $R\; n\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{R\}\; ^\; \{n\}\}$представлены векторами-столбцами , а ковекторы (линейные карты $R\; n\; \to \; R\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{R\}\; ^\; \{n\}\; \backslash \; to\; \backslash \; mathbf\; \{R\}\}$) представлены векторами-строками, градиент $\nabla \; f\; \{\backslash \; displaystyle\; \backslash \; nabla\; f\}$и производная $df\; \{\backslash \; displaystyle\; df\}$выражаются как вектор столбца и строки, соответственно, с теми же компонентами, но транспонированы друг друга:

$\nabla \; е\; (p)\; =\; [\partial \; f\; \partial \; x\; 1\; (p)\; ⋮\; \partial \; f\; \partial \; xn\; (p)]\; \{\backslash \; displaystyle\; \backslash \; nabla\; f\; (p)\; =\; \{\backslash \; begin\; \{bmatrix\}\; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; x\_\; \{1\}\}\}\; (p)\; \backslash \backslash \backslash \; vdots\; \backslash \backslash \; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; x\_\; \{n\}\}\}\; (p)\; \backslash \; end\; \{bmatrix\}\}\}$;

$dfp\; =\; [\partial \; е\; \partial \; x\; 1\; (p)\; \cdots \; \partial \; f\; \partial \; xn\; (p)]\; \{\backslash \; displaystyle\; df\_\; \{p\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; x\_\; \{\; 1\}\}\}\; (p)\; \backslash \; cdots\; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; x\_\; \{n\}\}\}\; (p)\; \backslash \; end\; \{bmatrix\}\}\}$.

Хотя они оба имеют одинаковые компоненты, они отличаются какой математический объект они представляют: в каждой точке производная - это вектор котангенса, линейная форма (ковектор ), которая выражает, насколько (скалярный) выходной сигнал изменяется для данного бесконечно малое изменение во входном (векторном), в то время как в каждой точке градиент представляет собой касательный вектор , который представляет бесконечно малое изменение во входном (векторном). В символах градиент является элементом касательного пространства в точке, $\nabla \; f\; (p)\; \in \; T\; p\; R\; n\; \{\backslash \; displaystyle\; \backslash \; nabla\; f\; (p)\; \backslash \; in\; T\_\; \{p\}\; \backslash \; mathbf\; \{R\}\; ^\; \{n\}\}$, в то время как производная - это отображение касательного пространства на действительные числа, $dfp:\; T\; p\; R\; n\; \to \; R\; \{\backslash \; displaystyle\; df\_\; \{p\}\; \backslash \; двоеточие\; T\_\; \{p\}\; \backslash \; mathbf\; \{R\}\; ^\; \{n\}\; \backslash \; to\; \backslash \; mathbf\; \{R\}\}$. Касательные пространства в каждой точке $R\; n\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{R\}\; ^\; \{n\}\}$могут быть «естественным образом» идентифицированы с векторным пространством $R\; n\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{R\}\; ^\; \{n\}\}$, и аналогичным образом котангенсное пространство в каждой точке можно естественным образом отождествить с двойным векторным пространством $(R\; n)\; \ast \; \{\backslash \; displaystyle\; (\backslash \; mathbf\; \{R\}\; ^\; \{n\})\; ^\; \{*\}\}$ковекторов; таким образом, значение градиента в точке можно рассматривать как вектор в исходном $R\; n\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{R\}\; ^\; \{n\}\}$, а не просто как касательный вектор.

Вычислительно, учитывая касательный вектор, вектор можно умножить на производную (в виде матриц), что эквивалентно взятию скалярного произведения с градиентом:

$(dfp)\; (v)\; =\; [\partial \; f\; \partial \; x\; 1\; (p)\; \cdots \; \partial \; f\; \partial \; xn\; (p)]\; [v\; 1\; ⋮\; vn]\; =\; \sum \; i\; =\; 1\; n\; \partial \; f\; \partial \; xi\; (p)\; vi\; =\; [\partial \; f\; \partial \; x\; 1\; (\; п)\; ⋮\; \partial \; е\; \partial \; xn\; (p)]\; \cdot \; [v\; 1\; ⋮\; vn]\; =\; \nabla \; f\; (p)\; \cdot \; v\; \{\backslash \; displaystyle\; (df\_\; \{p\})\; (v)\; =\; \{\backslash \; begin\; \{bmatrix\}\; \{\backslash \; frac\; \{\backslash \; частичный\; f\}\; \{\backslash \; partial\; x\_\; \{1\}\}\}\; (p)\; \backslash \; cdots\; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; x\_\; \{n\}\}\}\; (p)\; \backslash \; end\; \{bmatrix\}\}\; \{\backslash \; begin\; \{bmatrix\}\; v\_\; \{1\}\; \backslash \backslash \backslash \; vdots\; \backslash \backslash \; v\_\; \{n\}\; \backslash \; end\; \{bmatrix\}\}\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; x\_\; \{i\}\}\}\; (\; p)\; v\_\; \{i\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; x\_\; \{1\}\}\}\; (p)\; \backslash \backslash \backslash \; vdots\; \backslash \backslash \; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; x\_\; \{n\}\}\}\; (p)\; \backslash \; end\; \{bmatrix\}\}\; \backslash \; cdot\; \{\backslash \; begin\; \{bmatrix\}\; v\_\; \{1\}\; \backslash \backslash \backslash \; vdots\; \backslash \backslash \; v\_\; \{n\}\; \backslash \; end\; \{bmatrix\}\}\; =\; \backslash \; nabla\; f\; (p)\; \backslash \; cdot\; v\}$

Дифференциальная или (внешняя) производная

Наилучшее линейное приближение к дифференцируемой функции

$f:\; R\; n\; \to \; R\; \{\backslash \; displaystyle\; f\; \backslash \; двоеточие\; \backslash \; mathbf\; \{R\}\; ^\; \{n\; \}\; \backslash \; to\; \backslash \; mathbf\; \{R\}\}$

в точке x в R представляет собой линейное отображение от R до R, которое часто обозначается df x или Df ( x) и вызвал дифференциал или (total ) производное f в точке x. Функция df, которая отображает x в df x, называется (общий) дифференциал или внешней производной функции f и является примером дифференциальная 1-форма.

Так же, как производная функции одной переменной представляет собой наклон касательной к графику функции, производная по направлению функции нескольких переменных представляет собой наклон касательной гиперплоскости в направлении вектора.

Градиент связан с дифференциалом по формуле

$(\nabla \; f)\; x\; \cdot \; v\; =\; dfx\; (v)\; \{\backslash \; displaystyle\; (\backslash \; nabla\; f)\; \_\; \{x\}\; \backslash \; cdot\; v\; =\; df\_\; \{x\; \}\; (v)\}$

для любого v ∈ R, где $\cdot \; \{\backslash \; displaystyle\; \backslash \; cdot\}$- это скалярное произведение : принимая скалярное произведение вектора с градиентом аналогично взятию производной по направлению вдоль вектора.

Если R рассматривается как пространство векторов-столбцов (размерности n) (действительных чисел), то можно рассматривать df как вектор-строку с компонентами

$(\partial \; f\; \partial \; Икс\; 1,\dots ,\; \partial \; е\; \partial \; xn),\; \{\backslash \; displaystyle\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; x\_\; \{1\}\}\},\; \backslash \; dots,\; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; x\_\; \{n\}\}\}\; \backslash \; right),\}$

так, чтобы df x (v) было задано посредством умножения матриц. Предполагая стандартную евклидову метрику на R, тогда градиент является соответствующим вектором-столбцом, то есть

$(\nabla \; f)\; i\; =\; d\; f\; i\; T.\; \{\backslash \; displaystyle\; (\backslash \; nabla\; f)\; \_\; \{i\}\; =\; df\_\; \{i\}\; ^\; \{\backslash \; mathsf\; \{T\}\}.\}$

Линейное приближение к функции

Наилучшее линейное приближение к функции можно выразить через градиент, а не через производную. Градиент функции f от евклидова пространства R до R в любой конкретной точке x 0 в R характеризует наилучшее линейное приближение к f при x 0. Приближение выглядит следующим образом:

$f\; (x)\; \approx \; f\; (x\; 0)\; +\; (\nabla \; f)\; x\; 0\; \cdot \; (x\; -\; x\; 0)\; \{\backslash \; displaystyle\; f\; (x)\; \backslash \; приблизительно\; f\; (x\_\; \{0\})\; +\; (\backslash \; nabla\; f)\; \_\; \{x\_\; \{0\}\}\; \backslash \; cdot\; (x-x\_\; \{0\})\}$

для x, близкого к x 0, где (∇f) x0- градиент из f, вычисленного в x 0, а точка обозначает скалярное произведение на R . Это уравнение эквивалентно первым двум членам в многовариантном ряду Тейлора разложении f в x 0.

Градиент как «производная»

Пусть U будет открытым множеством в R . Если функция f: U → R является дифференцируемой, то дифференциал f является производной (Фреше) функции f. Таким образом, ∇f - это функция из U в пространство R такая, что

$lim\; h\; \to \; 0\; |\; f\; (x\; +\; h)\; -\; f\; (x)\; -\; f\; (x)\; \cdot \; h\; |\; \Vert \; Час\; \Vert \; знак\; равно\; 0,\; \{\backslash \; displaystyle\; \backslash \; lim\; \_\; \{h\; \backslash \; to\; 0\}\; \{\backslash \; frac\; \{|\; f\; (x\; +\; h)\; -f\; (x)\; -\; \backslash \; nabla\; f\; (x)\; \backslash \; cdot\; h\; |\}\; \{\backslash \; |\; h\; \backslash \; |\}\}\; =\; 0,\}$

где · - скалярное произведение.

Как следствие, обычные свойства производной сохраняются для градиента, хотя градиент сам по себе не является производной, а скорее двойственен производной:

Линейность

Градиент линейна в том смысле, что если f и g - две действительные функции, дифференцируемые в точке a ∈ R, а α и β - две константы, то αf + βg дифференцируема в точке a, и, более того,

$\nabla \; (\alpha \; f\; +\; \beta \; g)\; (a)\; =\; \alpha \; \nabla \; f\; (a)\; +\; \beta \; \nabla \; g\; (a).\; \{\backslash \; displaystyle\; \backslash \; nabla\; \backslash \; left\; (\backslash \; alpha\; f\; +\; \backslash \; beta\; g\; \backslash \; right)\; (a)\; =\; \backslash \; alpha\; \backslash \; nabla\; f\; (a)\; +\; \backslash \; beta\; \backslash \; nabla\; g\; (a).\}$

Правило продукта

Если f и g - вещественные функции, дифференцируемые в точке a ∈ R, то правило произведения утверждает, что произведение fg дифференцируемо в точке a, и

$\nabla \; (fg)\; (a)\; =\; f\; (a)\; \nabla \; g\; (a)\; +\; g\; (a)\; \nabla \; f\; (a).\; \{\backslash \; displaystyle\; \backslash \; nabla\; (fg)\; (a)\; =\; f\; (a)\; \backslash \; nabla\; g\; (a)\; +\; g\; (a)\; \backslash \; nabla\; f\; (a).\}$

Правило цепочки

Предположим, что f: A → R - это вещественная функция, определенная на подмножестве A из R, и что f дифференцируема в точке a. Есть две формы цепного правила, применяемого к градиенту. Сначала предположим, что функция g является параметрической кривой ; то есть функция g: I → R отображает подмножество I ⊂ R в R . Если g дифференцируема в такой точке c ∈ I, что g (c) = a, то

$(f\; \circ \; g)\; \prime \; (c)\; =\; \nabla \; f\; (a)\; \cdot \; g\; \prime \; (c),\; \{\backslash \; displaystyle\; (f\; \backslash \; circ\; g)\; \text{'}(c)\; =\; \backslash \; nabla\; f\; (a)\; \backslash \; cdot\; g\text{'}\; (c),\}$

где ∘ - оператор композиции : (f ∘ g) (x) = f (г (х)).

В более общем смысле, если вместо этого I ⊂ R, то имеет место следующее:

$\nabla \; (f\; \circ \; g)\; (c)\; =\; (D\; g\; (c))\; T\; (\nabla \; f\; (а)),\; \{\backslash \; displaystyle\; \backslash \; nabla\; (е\; \backslash \; circ\; g)\; (c)\; =\; \{\backslash \; big\; (\}\; Dg\; (c)\; \{\backslash \; big)\}\; ^\; \{\backslash \; mathsf\; \{T\}\}\; \{\backslash \; big\; (\}\; \backslash \; nabla\; f\; (a)\; \{\backslash \; big)\},\}$

где (Dg) обозначает транспонированную матрицу Якоби.

Для второй формы цепного правила предположим, что h: I → R - вещественнозначная функция на подмножестве I в R, и что h дифференцируема в точке f (a) ∈ I. Тогда

$\nabla \; (h\; \circ \; f)\; (a)\; =\; h\; \prime \; (\; f\; (a))\; \nabla \; f\; (a).\; \{\backslash \; displaystyle\; \backslash \; nabla\; (h\; \backslash \; circ\; f)\; (a)\; =\; h\; \text{'}\{\backslash \; big\; (\}\; f\; (a)\; \{\backslash \; big)\}\; \backslash \; nabla\; f\; (a).\}$

Другие свойства и приложения

Наборы уровней

Поверхность уровня или изоповерхность - это набор всех точек, в которых некоторая функция имеет заданное значение.

Если f дифференцируема, то скалярное произведение (∇f) x ⋅ v градиента в точке x с вектором v дает производную по направлению от f в точке x в направлении v. Отсюда следует, что в этом случае градиент f является ортогональным к наборам уровня f. Например, поверхность уровня в трехмерном пространстве определяется уравнением вида F (x, y, z) = c. Тогда градиент F нормален к поверхности.

В более общем смысле любая встроенная гиперповерхность в риманово многообразие может быть вырезана уравнением вида F (P) = 0, так что dF нигде не равно нулю.. Тогда градиент F нормален к гиперповерхности.

Аналогично, аффинная алгебраическая гиперповерхность может быть определена уравнением F (x 1,..., x n) = 0, где F - полином. Градиент F равен нулю в особой точке гиперповерхности (это определение особой точки). В неособой точке это ненулевой нормальный вектор.

Консервативные векторные поля и градиентная теорема

Градиент функции называется градиентным полем. (Непрерывное) поле градиента всегда является консервативным векторным полем : его линейный интеграл вдоль любого пути зависит только от конечных точек пути и может быть вычислен с помощью градиентной теоремы ( основная теорема исчисления для линейных интегралов). И наоборот, (непрерывное) консервативное векторное поле всегда является градиентом функции.

Матрица Якоби - это обобщение градиента для векторнозначных функций нескольких переменных и дифференцируемых карт между евклидовыми пробелы или, в более общем смысле, многообразия. Дальнейшее обобщение функции между банаховыми пространствами - это производная Фреше.

Градиент вектора

Поскольку полная производная векторного поля является линейным отображением от векторов к векторам, это тензор величина.

В прямоугольных координатах градиент векторного поля f = (f, f, f) определяется следующим образом:

$\nabla \; f\; =\; gjk\; \partial \; fi\; \partial \; xjei\; \otimes \; ek,\; \{\; \backslash \; displaystyle\; \backslash \; nabla\; \backslash \; mathbf\; \{f\}\; =\; g\; ^\; \{jk\}\; \{\backslash \; frac\; \{\backslash \; partial\; f\; ^\; \{i\}\}\; \{\backslash \; partial\; x\; ^\; \{j\}\}\}\; \backslash \; mathbf\; \{e\}\; \_\; \{i\}\; \backslash \; otimes\; \backslash \; mathbf\; \{e\}\; \_\; \{k\},\}$

(где используется нотация суммирования Эйнштейна, а тензорное произведение векторов eiи ekравно диадический тензор типа (2,0)). В целом, это выражение равно транспонированной матрице Якоби:

$\partial \; f\; i\; \partial \; x\; j\; =\; \partial \; (f\; 1,\; f\; 2,\; f\; 3)\; \partial \; (x\; 1,\; x\; 2,\; x\; 3).\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; f\; ^\; \{i\}\}\; \{\backslash \; partial\; x\; ^\; \{j\}\}\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; (f\; ^\; \{1\},\; f\; ^\; \{2\},\; f\; ^\; \{3\})\}\; \{\backslash \; partial\; (x\; ^\; \{1\},\; x\; ^\; \{2\},\; x\; ^\; \{3\})\}\}.\}$

В криволинейных координатах или, в более общем смысле, на изогнутом многообразии градиент включает символы Кристоффеля :

$\nabla \; f\; =\; gjk\; (\partial \; fi\; \partial \; xj\; +\; \Gamma \; ijlfl)\; ei\; \otimes \; ek,\; \{\backslash \; displaystyle\; \backslash \; nabla\; \backslash \; mathbf\; \{f\}\; =\; g\; ^\; \{jk\}\; \backslash \; left\; (\{\backslash \; frac\; \{\; \backslash \; partial\; f\; ^\; \{i\}\}\; \{\backslash \; partial\; x\; ^\; \{j\}\}\}\; +\; \{\backslash \; Gamma\; ^\; \{i\}\}\; \_\; \{jl\}\; f\; ^\; \{l\}\; \backslash \; right)\; \backslash \; mathbf\; \{e\}\; \_\; \{i\}\; \backslash \; otimes\; \backslash \; mathbf\; \{e\}\; \_\; \{k\},\}$

где g - компоненты обратного метрического тензора , а ei- координатные базисные векторы.

Выражаясь более инвариантно, градиент векторного поля f может быть определен связью Леви-Чивиты и метрическим тензором:

$\nabla \; afb\; =\; gac\; \nabla \; cfb,\; \{\backslash \; displaystyle\; \backslash \; nabla\; ^\; \{a\}\; f\; ^\; \{b\}\; =\; g\; ^\; \{ac\}\; \backslash \; nabla\; \_\; \{c\}\; f\; ^\; \{b\},\}$

, где ∇ c - соединение.

Римановы многообразия

Для любой гладкой функции f на римановом многообразии (M, g) градиент f - это векторное поле ∇f такое, что для любого вектора поле X,

$g\; (\nabla \; f,\; X)\; =\; \partial \; X\; f,\; \{\backslash \; displaystyle\; g\; (\backslash \; nabla\; f,\; X)\; =\; \backslash \; partial\; \_\; \{X\}\; f,\}$

то есть

$gx\; (\; (\nabla \; е)\; Икс,\; Икс\; Икс)\; знак\; равно\; (\partial \; Икс\; е)\; (Икс),\; \{\backslash \; Displaystyle\; g\_\; \{x\}\; \{\backslash \; big\; (\}\; (\backslash \; nabla\; f)\; \_\; \{x\},\; X\_\; \{x\}\; \{\backslash \; big)\}\; =\; (\backslash \; partial\; \_\; \{X\}\; f)\; (x),\}$

где g x (,) обозначает внутреннее произведение касательных векторов в точке x, определенных метрикой g и ∂ X f - функция, которая переводит любую точку x ∈ M в производную f по направлению в направлении X, вычисленную в x. Другими словами, в координатной карте φ от открытого подмножества M до открытого подмножества R, (∂ X f) (x) задается по:

$\sum \; j\; =\; 1\; n\; X\; j\; (\phi \; (x))\; \partial \; \partial \; xj\; (f\; \circ \; \phi \; -\; 1)\; |\; \phi \; (Икс),\; \{\backslash \; Displaystyle\; \backslash \; сумма\; \_\; \{J\; =\; 1\}\; ^\; \{n\}\; X\; ^\; \{J\}\; \{\backslash \; big\; (\}\; \backslash \; varphi\; (x)\; \{\backslash \; big)\}\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; x\_\; \{j\}\}\}\; (f\; \backslash \; circ\; \backslash \; varphi\; ^\; \{-\; 1\})\; \{\backslash \; Bigg\; |\}\; \_\; \{\backslash \; varphi\; (x)\},\}$

где X обозначает j-й компонент X в этой координатной диаграмме.

Итак, локальная форма градиента принимает вид:

$\nabla \; f\; =\; g\; i\; k\; \partial \; f\; \partial \; x\; k\; e\; i.\; \{\backslash \; displaystyle\; \backslash \; nabla\; f\; =\; g\; ^\; \{ik\}\; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; x\; ^\; \{k\}\}\}\; \{\backslash \; textbf\; \{e\}\}\; \_\; \{i\}.\}$

Обобщение случая M = R, градиент функции связан с ее внешней производной, поскольку

$(\partial \; X\; f)\; (x)\; =\; (df)\; x\; (X\; x).\; \{\backslash \; displaystyle\; (\backslash \; partial\; \_\; \{X\}\; f)\; (x)\; =\; (df)\; \_\; \{x\}\; (X\_\; \{x\}).\}$

Точнее, градиент ∇f - это векторное поле, связанное с дифференциалом 1 -form df, используя музыкальный изоморфизм

$♯\; =\; ♯\; g:\; T\; \ast \; M\; \to \; TM\; \{\backslash \; displaystyle\; \backslash \; sharp\; =\; \backslash \; sharp\; ^\; \{g\}\; \backslash \; двоеточие\; T\; ^\; \{*\}\; M\; \backslash \; to\; TM\}$

(называемые «точными»), определяемые метрикой g. Связь между внешней производной и градиентом функции на R является частным случаем этого, в котором метрика является плоской метрикой, заданной скалярным произведением.

На Викискладе есть материалы, связанные с Градиентными полями.

• Curl
• Дивергенцией
• Четырехградиентной
• матрицей Гессе
• Косым градиентом

• Бахман, Дэвид (2007), Advanced Calculus Demystified, New York: McGraw-Hill, ISBN 978-0 -07-148121-2
• Beauregard, Raymond A.; Фрали, Джон Б. (1973), Первый курс линейной алгебры: с дополнительным введением в группы, кольца и поля, Бостон: Houghton Mifflin Company, ISBN 0-395-14017-X
• Даунинг, Дуглас, доктор философии. (2010), Barron's E-Z Calculus, Нью-Йорк: Barron's, ISBN 978-0-7641-4461-5
• Dubrovin, B.A.; Фоменко, А. Т.; Новиков, С. П. (1991). Современная геометрия - методы и приложения: Часть I: Геометрия поверхностей, группы преобразований и поля. Тексты для выпускников по математике (2-е изд.). Springer. ISBN 978-0-387-97663-1. CS1 maint: ref = harv (ссылка )
• Харпер, Чарли (1976), Введение в математику Physics, Нью-Джерси: Прентис-Холл, ISBN 0-13-487538-9
• Крейсиг, Эрвин (1972), Advanced Engineering Mathematics (3-е изд.), Нью-Йорк: Wiley, ISBN 0-471-50728-8
• «Энциклопедия науки и техники МакГроу Хилла». McGraw-Hill Encyclopedia of Science Technology (10-е изд.). Нью-Йорк: McGraw-Hill. 2007. ISBN 978-0-07-144143-8.
• Моис, Эдвин Э. (1967), Исчисление: Полное, Литература: Аддисон-Уэсли
• Проттер, Мюррей Х.; Морри-младший, Чарльз Б. (1970), Колледж-исчисление с аналитической геометрией ( 2-е изд.), Чтение: Аддисон-Уэсли, LCCN 76087042
• Schey, HM (1992). Div, Grad, Curl, and All That (2-е изд.). WW Norton. ISBN 0-393-96251-2. OCLC 25048561. CS1 maint: ref = harv (ссылка )
• Сток р, Дж. Дж. (1969), Дифференциальная геометрия, Нью-Йорк: Wiley, ISBN 0-471-82825-4
• Своковски, Эрл У.; Олиник, Майкл; Пенс, Деннис; Коул, Джеффри А. (1994), Calculus (6-е изд.), Бостон: PWS Publishing Company, ISBN 0-534-93624-5

• Корн, Тереза ​​М.; Корн, Гранино Артур (2000). Математический справочник для ученых и инженеров: определения, теоремы и формулы для справки и обзора. Dover Publications. С. 157–160. ISBN 0-486-41147-8. OCLC 43864234. CS1 maint: ref = harv (ссылка )

Искать градиент в Викисловаре, бесплатный словарь.

• «Градиент». Академия Хана.
• Купцов, Л.П. (2001) [1994], Энциклопедия математики, EMS Press.
• Weisstein, Eric W. «Градиент». MathWorld.