Интеграл по строке

редактировать

В математике интеграл по строке является интегралом где функция, которую нужно интегрировать, оценивается по кривой . Также используются термины интеграл по путям, интеграл по кривой и криволинейный интеграл; контурный интеграл также используется, хотя он обычно зарезервирован для линейных интегралов в комплексной плоскости.

Интегрируемой функцией может быть скалярное поле или векторное поле. Значение линейного интеграла - это сумма значений поля во всех точках кривой, взвешенных некоторой скалярной функцией на кривой (обычно длина дуги или, для векторного поля, скалярное произведение векторного поля с дифференциальным вектором на кривой). Это взвешивание отличает линейный интеграл от более простых интегралов, определенных на интервалах. Многие простые формулы в физике, такие как определение , работают как $W = F ⋅ s {\ displaystyle W = \ mathbf {F} \ cdot \ mathbf {s}}$ ${\ displaystyle W = \ mathbf {F} \ cdot \ mathbf {s}}$ , имеют естественные непрерывные аналоги в терминах линейных интегралов, в данном случае $W = ∫ LF (s) ⋅ ds {\ displaystyle \ textstyle W = \ int _ {L} \ mathbf {F} (\ mathbf {s }) \ cdot d \ mathbf {s}}$ ${\ displaystyle \ textstyle W = \ int _ {L} \ mathbf {F} (\ mathbf {s}) \ cdot d \ mathbf {s}}$ , который вычисляет работу, выполняемую над объектом, движущимся в электрическом или гравитационном поле F по пути s.

Содержание

1 Векторное исчисление
- 1.1 Линейный интеграл скалярного поля
  - 1.1.1 Определение
  - 1.1.2 Выведение
- 1.2 Линейный интеграл векторного поля
  - 1.2.1 Определение
  - 1.2.2 Выведение
- 1.3 Независимость от пути
- 1.4 Приложения
2 Поток по кривой
3 Комплексный линейный интеграл
- 3.1 Пример
- 3.2 Связь комплексного линейного интеграла и линейного интеграла векторного поля
4 Квантовая механика
5 См. также
6 Ссылки
7 Внешние ссылки

Векторное исчисление

В качественном выражении линия в Теграл в векторном исчислении можно рассматривать как меру общего эффекта заданного тензорного поля вдоль заданной кривой. Например, линейный интеграл по скалярному полю (тензор ранга 0) можно интерпретировать как площадь под полем, вырезанную определенной кривой. Это можно визуализировать как поверхность, созданную z = f (x, y) и кривой C в плоскости xy. Интеграл по линии f будет площадью созданной «завесы» - когда точки поверхности, которые находятся непосредственно над C, вырезаны.

Линейный интеграл скалярного поля

Линейный интеграл по скалярному полю f можно представить как площадь под кривой C вдоль поверхности z = f (x, y), описываемой полем.

Определение

Для некоторого скалярного поля $f: U ⊆ R n → R {\ displaystyle f: \ mathbb {U} \ substeq \ mathbb {R} ^ {n} \ rightarrow \ mathbb {R}}$ ${\ displaystyle е: \ mathbb {U} \ substeq \ mathbb {R} ^ {n} \ rightarrow \ mathbb {R}}$ , линейный интеграл вдоль кусочно-гладкой кривой $C ⊂ U {\ displaystyle {\ mathcal {C}} \ subset \ mathbb {U}}$ ${\ Displaystyle {\ mathcal {C}} \ subset \ mathbb {U}}$ определяется как

∫ C f (r) ds = ∫ abf (r (t)) | r ′ (t) | д т. {\ displaystyle \ int _ {\ mathcal {C}} f (\ mathbf {r}) \, ds = \ int _ {a} ^ {b} f \ left (\ mathbf {r} (t) \ right) | \ mathbf {r} '(t) | \, dt.}

\int _{\mathcal {C}}f(\mathbf {r})\,ds=\int _{a}^{b}f\left(\mathbf {r} (t)\right)|\mathbf {r} '(t)|\,dt.

где $r: [a, b] → C {\ displaystyle \ mathbf {r}: [a, b] \ rightarrow {\ mathcal {C}}}$ ${\ displaystyle \ mathbf {r}: [a, b] \ rightarrow {\ mathcal {C }}}$ - произвольная биективная параметризация кривой $C {\ displaystyle {\ mathcal {C}}}$ ${\ mathcal {C}}$ такие, что $r (a) {\ displaystyle \ mathbf {r} (a)}$ ${\ displaystyle \ mathbf {r} (a)}$ и $r (b) {\ displaystyle \ mathbf {r} (b)}$ ${\ displaystyle \ mathbf {r} (b)}$ задайте конечные точки $C {\ displaystyle {\ mathcal {C}}}$ ${\ mathcal {C}}$ и $a < b {\displaystyle a$ $a <b$ . Здесь и в остальной части статьи столбцы абсолютных значений обозначают стандартную (евклидову) норму вектора.

Функция $f {\ displaystyle f}$ $f$ называется подынтегральным выражением, кривая $C {\ displaystyle {\ mathcal {C}}}$ ${\ mathcal {C}}$ - это область интегрирования, а символ $ds {\ displaystyle ds}$ $ds$ можно интуитивно интерпретировать как элементарную длину дуги. Линейные интегралы скалярных полей по кривой $C {\ displaystyle {\ mathcal {C}}}$ ${\ mathcal {C}}$ не зависят от выбранной параметризации $r {\ displaystyle \ mathbf {r}}$ $\ mathbf {r}$ из $C {\ displaystyle {\ mathcal {C}}}$ ${\ mathcal {C}}$ .

Геометрически, когда скалярное поле $f {\ displaystyle f}$ $f$ определено на плоскости $(n = 2) {\ displaystyle (n = 2)}$ ${\ Displaystyle (п = 2)}$ , его график представляет собой поверхность $z = f (x, y) {\ displaystyle z = f (x, y)}$ $z = f (x, y)$ в пространстве, а линейный интеграл дает (со знаком) площадь поперечного сечения, ограниченную кривой $C {\ displaystyle {\ mathcal {C}}}$ ${\ mathcal {C}}$ и график $f {\ displaystyle f}$ $f$ . Смотрите анимацию справа.

Вывод

Для линейного интеграла по скалярному полю интеграл может быть построен из суммы Римана с использованием приведенных выше определений f, C и параметризации r из C. Это может быть выполнено путем разделения интервала [a, b] на n подинтервалов [t i-1, t i ] длины Δt = (b - a) / n, тогда r(ti) обозначает некоторую точку, называемую точкой выборки, на кривой C. Мы можем использовать набор точек выборки { r(ti): 1 ≤ i ≤ n} для аппроксимации кривой C многоугольным путем путем введения отрезка прямой линии между каждой из точек выборки r(ti-1) и r(ti). Затем мы помечаем расстояние между каждой из точек выборки на кривой как Δs i. Произведение f (r(ti)) и Δs i может быть связано с подписанной областью прямоугольника с высотой и шириной f (r(ti)) и Δs i соответственно. Если взять предел для суммы членов, когда длина разделов приближается к нулю, получаем

I = lim Δ si → 0 ∑ i = 1 nf (r (ti)) Δ si. {\ displaystyle I = \ lim _ {\ Delta s_ {i} \ rightarrow 0} \ sum _ {i = 1} ^ {n} f (\ mathbf {r} (t_ {i})) \, \ Delta s_ {i}.}

{\ displaystyle I = \ lim _ { \ Delta s_ {i} \ rightarrow 0} \ sum _ {i = 1} ^ {n} f (\ mathbf {r} (t_ {i})) \, \ Delta s_ {i}.}

Согласно теореме о среднем значении расстояние между последующими точками на кривой равно

Δ si = | r (t i + Δ t) - r (t i) | ≈ | r ′ (t i) | Δ т. {\ displaystyle \ Delta s_ {i} = | \ mathbf {r} (t_ {i} + \ Delta t) - \ mathbf {r} (t_ {i}) | \ приблизительно | \ mathbf {r} '(t_ {i}) | \, \ Delta t.}

\Delta s_{i}=|\mathbf {r} (t_{i}+\Delta t)-\mathbf {r} (t_{i})|\approx |\mathbf {r} '(t_{i})|\,\Delta t.

Подставляя это в приведенную выше сумму Римана, получаем

I = lim Δ t → 0 ∑ i = 1 nf (r (ti)) | r ′ (t i) | Δ T {\ Displaystyle I = \ lim _ {\ Delta t \ rightarrow 0} \ sum _ {i = 1} ^ {n} f (\ mathbf {r} (t_ {i})) | \ mathbf {r} '(t_ {i}) | \, \ Delta t}

I=\lim _{\Delta t\rightarrow 0}\sum _{i=1}^{n}f(\mathbf {r} (t_{i}))|\mathbf {r} '(t_{i})|\,\Delta t

, которая представляет собой сумму Римана для интеграла

I = ∫ abf (r (t)) | r ′ (t) | д т. {\ displaystyle I = \ int _ {a} ^ {b} f (\ mathbf {r} (t)) | \ mathbf {r} '(t) | \, dt.}

I=\int _{a}^{b}f(\mathbf {r} (t))|\mathbf {r} '(t)|\,dt.

Линейный интеграл вектора поле

Определение

Для векторного поля F: U ⊆ R→ R, линейный интеграл вдоль кусочно-гладкой кривой C ⊂ U в направлении r определяется как

∫ CF (r) ⋅ dr = ∫ ab F (r (t)) ⋅ r ′ (t) dt. {\ displaystyle \ int _ {C} \ mathbf {F} (\ mathbf {r}) \ cdot \, d \ mathbf {r} = \ int _ {a} ^ {b} \ mathbf {F} (\ mathbf {r} (t)) \ cdot \ mathbf {r} '(t) \, dt.}

\int _{C}\mathbf {F} (\mathbf {r})\cdot \,d\mathbf {r} =\int _{a}^{b}\mathbf {F} (\mathbf {r} (t))\cdot \mathbf {r} '(t)\,dt.

, где · - скалярное произведение, а r : [a, b] → C - это биективная параметризация кривой C, такая что r (a) и r (b) дают конечные точки C.

Линейный интеграл скалярного поля, таким образом, является линейным интегралом векторного поля, где векторы всегда касательны к линии.

Линейные интегралы векторных полей не зависят от параметризации r в абсолютном значении, но они зависят от его ориентации. В частности, изменение ориентации параметризации меняет знак линейного интеграла.

С точки зрения дифференциальной геометрии линейный интеграл векторного поля вдоль кривой является интегралом соответствующей 1-формы при музыкальном изоморфизме (который переводит векторное поле в соответствующее ковекторное поле) по кривой, рассматриваемой как погруженный 1- многообразие.

Вывод

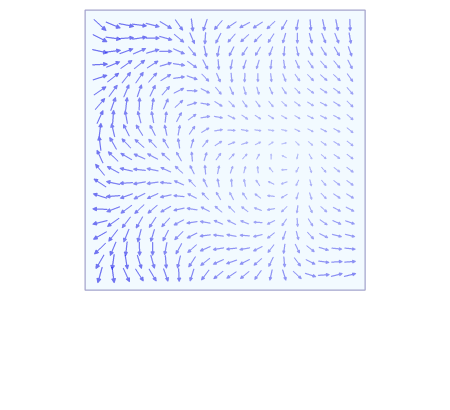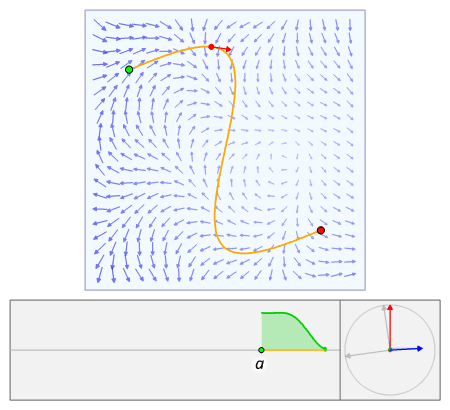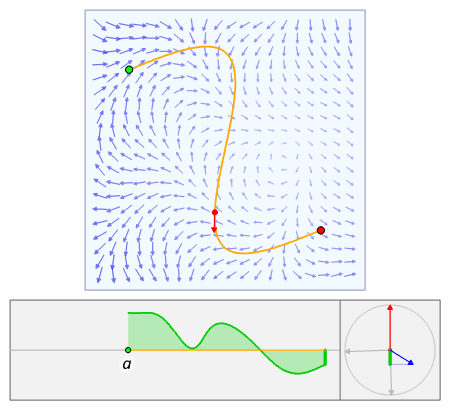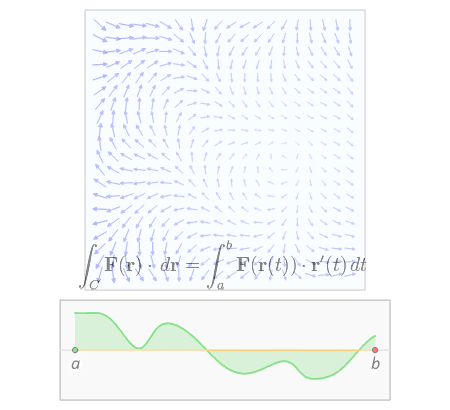
Траектория частицы (выделена красным) по кривой внутри векторного поля. Начиная с a, частица прослеживает путь C вдоль векторного поля F. Точечное произведение (зеленая линия) своего касательного вектора (красная стрелка) и вектора поля (синяя стрелка) определяет область под кривой, которая эквивалентна интеграл линии пути. (Щелкните изображение для получения подробного описания.)

Линейный интеграл векторного поля может быть получен способом, очень похожим на случай скалярного поля, но на этот раз с включением скалярного произведения. Снова используя приведенные выше определения F, C и его параметризацию r (t), мы строим интеграл из суммы Римана. Мы разбиваем интервал [a, b] (который является диапазоном значений параметра t) на n интервалов длиной Δt = (b - a) / n. Если t i быть i-й точкой на [a, b], тогда r(ti) дает нам положение i-й точки на кривой. Однако вместо вычисления расстояний между последующими точками нам нужно вычислить их векторы смещения , Δ ri. Как и раньше, оценка F во всех точках кривой и взятие скалярного произведения с каждым вектором смещения дает нам бесконечно малый вклад каждого раздела F на C. Обнуление размера разделов дает нам сумму

I = lim Δ t → 0 ∑ i = 1 n F (r (ti)) ⋅ Δ ri {\ displaystyle I = \ lim _ {\ Delta t \ rightarrow 0} \ sum _ {i = 1} ^ {n} \ mathbf {F} (\ mathbf {r} (t_ {i})) \ cdot \ Delta \ mathbf {r} _ {i}}

I = \ lim _ {\ Delta t \ rightarrow 0} \ sum _ {i = 1} ^ {n} \ mathbf {F} (\ mathbf {r} (t_ {i})) \ cdot \ Delta \ mathbf {г} _ {я}

По теореме о среднем значении мы видим, что вектор смещения между соседними точками на кривой равен

Δ ri = r (ti + Δ t) - r (ti) ≈ r ′ ( ti) Δ t. {\ displaystyle \ Delta \ mathbf {r} _ {i} = \ mathbf {r} (t_ {i} + \ Delta t) - \ mathbf {r} (t_ {i}) \ приблизительно \ mathbf {r} ' (t_ {i}) \, \ Delta t.}

\Delta \mathbf {r} _{i}=\mathbf {r} (t_{i}+\Delta t)-\mathbf {r} (t_{i})\approx \mathbf {r} '(t_{i})\,\Delta t.

Подставляя это в сумму Римана выше, получаем

I = lim Δ t → 0 ∑ i = 1 n F (r (ti)) ⋅ r ′ ( ti) Δ T, {\ displaystyle I = \ lim _ {\ Delta t \ rightarrow 0} \ sum _ {i = 1} ^ {n} \ mathbf {F} (\ mathbf {r} (t_ {i})) \ cdot \ mathbf {r} '(t_ {i}) \, \ Delta t,}

I=\lim _{\Delta t\rightarrow 0}\sum _{i=1}^{n}\mathbf {F} (\mathbf {r} (t_{i}))\cdot \mathbf {r} '(t_{i})\,\Delta t,

, которая является суммой Римана для интеграла, определенного выше.

Независимость от пути

Если векторное поле F является градиентом скалярного поля G (т.е. если F является консервативным ), то есть

F = ∇ G, {\ displaystyle \ mathbf {F} = \ nabla G,}

{\ displaystyle \ mathbf {F} = \ nabla G,}

, затем производная композиции группы G и r (t) равно

d G (r (t)) dt = ∇ G (r (t)) ⋅ r ′ ( t) знак равно F (r (t)) ⋅ r ′ (t) {\ displaystyle {\ frac {dG (\ mathbf {r} (t))} {dt}} = \ nabla G (\ mathbf {r} ( t)) \ cdot \ mathbf {r} '(t) = \ mathbf {F} (\ mathbf {r} (t)) \ cdot \ mathbf {r}' (t)}

{\frac {dG(\mathbf {r} (t))}{dt}}=\nabla G(\mathbf {r} (t))\cdot \mathbf {r} '(t)=\mathbf {F} (\mathbf {r} (t))\cdot \mathbf {r} '(t)

, который оказывается подынтегральное выражение для линейного интеграла F на r (t). Отсюда следует, что для пути C

∫ CF (r) ⋅ dr = ∫ ab F (r (t)) ⋅ r ′ (t) dt = ∫ abd G (r (t)) dtdt = G ( г (б)) - G (г (а)). {\ displaystyle \ int _ {C} \ mathbf {F} (\ mathbf {r}) \ cdot \, d \ mathbf {r} = \ int _ {a} ^ {b} \ mathbf {F} (\ mathbf {r} (t)) \ cdot \ mathbf {r} '(t) \, dt = \ int _ {a} ^ {b} {\ frac {dG (\ mathbf {r} (t))} {dt }} \, dt = G (\ mathbf {r} (b)) - G (\ mathbf {r} (a)).}

\int _{C}\mathbf {F} (\mathbf {r})\cdot \,d\mathbf {r} =\int _{a}^{b}\mathbf {F} (\mathbf {r} (t))\cdot \mathbf {r} '(t)\,dt=\int _{a}^{b}{\frac {dG(\mathbf {r} (t))}{dt}}\,dt=G(\mathbf {r} (b))-G(\mathbf {r} (a)).

Другими словами, интеграл от F по C зависит исключительно от значений G в точках r (b) и r (a) и, таким образом, не зависит от пути между ними. По этой причине линейный интеграл консервативного векторного поля называется независимым от пути.

Приложения

Линейный интеграл находит множество применений в физике. Например, работа, проделанная над частицей, движущейся по кривой C внутри силового поля, представленного как векторное поле F, является линейным интегралом от F на C.

Обтекание кривой

Для векторного поля $F: U ⊂ R 2 → R 2 {\ displaystyle \ mathbf {F}: U \ подмножество \ mathbb {R} ^ {2} \ to \ mathbb {R} ^ {2}}$ ${\ displaystyle \ mathbf {F}: U \ subset \ mathbb {R} ^ {2} \ to \ mathbb {R} ^ {2}}$ , $F (x, y) = (P (x, y), Q (x, y)) {\ displaystyle \ mathbf {F} (x, y) = (P (x, y), Q (x, y))}$ ${\ displaystyle \ mathbf {F} (x, y) = (P (x, y), Q (x, y))}$ , линейный интеграл через кривую C ⊂ U, также называемый интегралом потока, определяется в терминах кусочно-гладкой параметризации $r: [a, b] → C, {\ displaystyle \ mathbf {r} \ двоеточие [a, b] \ к C,}$ ${\ displaystyle \ mathbf {r} \ двоеточие [a, b] \ в C,}$ $r (t) = (x (t), y (t)), {\ displaystyle \ mathbf {r} (t) = (x (t), y (t)),}$ ${\ displaystyle \ mathbf {r} (t) = (x (t), y ( t)),}$ как:

∫ CF (r) ⋅ dr ⊥ = ∫ ab (P (x (t), y (t)), Q (x (t), y (t))) ⋅ (y ′ (t), - x ′ (t)) dt = ∫ ab - Q dx + P dy. {\ displaystyle \ int _ {C} \ mathbf {F} (\ mathbf {r}) \ cdot d \ mathbf {r} ^ {\ perp} = \ int _ {a} ^ {b} (P (x ( t), y (t)), Q (x (t), y (t))) \ cdot (y '(t), - x' (t)) \, dt = \ int _ {a} ^ { b} -Q \, dx + P \, dy.}

\int _{C}\mathbf {F} (\mathbf {r})\cdot d\mathbf {r} ^{\perp }=\int _{a}^{b}(P(x(t),y(t)),Q(x(t),y(t)))\cdot (y'(t),-x'(t))\,dt=\int _{a}^{b}-Q\,dx+P\,dy.

Здесь • - скалярное произведение, а $r ′ (t) ⊥ = (y ′ (t), - x ′ (t)) { \ displaystyle \ mathbf {r} '(t) ^ {\ perp} = (y' (t), - x '(t))}$ $\mathbf {r} '(t)^{\perp }=(y'(t),-x'(t))$ - перпендикуляр по часовой стрелке к вектору скорости $r ′ (T) = (x ′ (t), y ′ (t)) {\ displaystyle \ mathbf {r} '(t) = (x' (t), y '(t))}$ $\mathbf {r} '(t)=(x'(t),y'(t))$ .

Поток вычисляется в ориентированном смысле: кривая C имеет заданное прямое направление от r (a) до r (b), и поток считается положительным, когда $F (r (t)) {\ displaystyle \ mathbf {F} (\ mathbf {r} (t))}$ ${\ displaystyle \ mathbf {F} (\ mathbf {r} (t))}$ находится по часовой стрелке от вектора скорости движения $r ′ (t) { \ displaystyle \ mathbf {r} '(t)}$ $\mathbf {r} '(t)$ .

Комплексный линейный интеграл

В комплексном анализе линейный интеграл определяется в терминах умножения и сложение комплексных чисел. Предположим, что U - открытое подмножество комплексной плоскости C, f: U → C - функция, и $L ⊂ U {\ displaystyle L \ подмножество U}$ $L \ subset U$ - кривая конечной длины, параметризованная как $γ: [a, b] → L {\ displaystyle \ gamma: [a, b] \ to L}$ $\ gamma: [a, b] \ к L$ , где $γ (t) = x (t) + iy (t). {\ displaystyle \ gamma (t) = x (t) + iy (t).}$ $\ gamma (t) = x (t) + iy (t).$ Интеграл по прямой

∫ L f (z) dz {\ displaystyle \ int _ {L} f ( z) \, dz}

\ int _ {L} е (z) \, dz

можно определить, разделив интервал [a, b] на a = t 0< t1<... < tn= b и учитывая выражение

∑ k = 1 nf (γ (tk)) [γ (tk) - γ (tk - 1)] = ∑ k = 1 nf (γ k) Δ γ k. {\ Displaystyle \ сумма _ {к = 1} ^ {п} е (\ гамма (т_ {к})) \, [\ гамма (т_ {к}) - \ гамма (т_ {к-1})] = \ sum _ {k = 1} ^ {n} f (\ gamma _ {k}) \, \ Delta \ gamma _ {k}.}

{\ displaystyle \ sum _ {k = 1} ^ {n} f (\ gamma (t_ {k})) \, [\ gamma (t_ {k}) - \ gamma (t_ {k-1})] = \ sum _ {k = 1} ^ {n} f (\ гамма _ {k}) \, \ Delta \ gamma _ {k}.}

Тогда интеграл является пределом этой суммы Римана, когда длины интервалов подразделения приближаются к нулю.

Если параметризация $γ {\ displaystyle \ gamma}$ $\ gamma$ является непрерывно дифференцируемой, линейный интеграл может быть вычислен как интеграл от функции действительного переменная:

∫ L f (z) dz = ∫ abf (γ (t)) γ ′ (t) dt. {\ displaystyle \ int _ {L} f (z) \, dz = \ int _ {a} ^ {b} f (\ gamma (t)) \ gamma '(t) \, dt.}

\int _{L}f(z)\,dz=\int _{a}^{b}f(\gamma (t))\gamma '(t)\,dt.

Когда $L {\ displaystyle L}$ $L$ - замкнутая кривая (начальная и конечная точки совпадают), линейный интеграл часто обозначается $∮ L f (z) dz, {\ displaystyle \ textstyle \ oint _ {L} f (z) \, dz,}$ ${\ displaystyle \ textstyle \ oint _ {L} f (z) \, dz,}$ , иногда называемый в технике циклическим интегралом.

Линейный интеграл относительно сопряженного комплексного дифференциала $dz ¯ {\ displaystyle {\ overline {dz}}}$ ${\ overline {dz}}$ определяется как

∫ L f (z) dz ¯: = ∫ L f (z) ¯ dz ¯ = ∫ abf (γ (t)) γ ′ (t) ¯ dt. {\ Displaystyle \ int _ {L} е (z) {\ overline {dz}}: = {\ overline {\ int _ {L} {\ overline {f (z)}} \, dz}} = \ int _ {a} ^ {b} f (\ gamma (t)) {\ overline {\ gamma '(t)}} \, dt.}

\int _{L}f(z){\overline {dz}}:={\overline {\int _{L}{\overline {f(z)}}\,dz}}=\int _{a}^{b}f(\gamma (t)){\overline {\gamma '(t)}}\,dt.

Линейные интегралы комплексных функций могут быть вычислены с использованием ряда методов. Самый простой - разделить на действительную и мнимую части, сведя задачу к вычислению двух линейных интегралов с действительными значениями. Интегральная теорема Коши может использоваться, чтобы приравнять линейный интеграл аналитической функции к тому же интегралу по более удобной кривой. Это также означает, что по замкнутой кривой, охватывающей область, где $f (z) {\ displaystyle f (z)}$ $f (z)$ является аналитическим без сингулярностей, значение интеграла равно просто ноль, или в случае, если область включает особенности, теорема вычетов вычисляет интеграл в терминах сингулярностей.

Пример

Рассмотрим функцию f (z) = 1 / z, и пусть контур L представляет собой единичную окружность против часовой стрелки около 0, параметризованную z (t) = e с t в [0, 2π] с использованием комплексной экспоненты. Подставляя, находим:

∮ L 1 z d z = ∫ 0 2 π 1 e i t i e i t d t = i ∫ 0 2 π e - i t e i t d t = i ∫ 0 2 π d t = i (2 π - 0) = 2 π i. {\ displaystyle {\ begin {align} \ oint _ {L} {\ frac {1} {z}} \, dz = \ int _ {0} ^ {2 \ pi} {\ frac {1} {e ^ {it}}} т.е. ^ {it} \, dt = i \ int _ {0} ^ {2 \ pi} e ^ {- it} e ^ {it} \, dt \\ = i \ int _ { 0} ^ {2 \ pi} dt = i (2 \ pi -0) = 2 \ pi i. \ End {align}}}

{\ displaystyle {\ begin {align} \ oint _ {L} {\ frac {1} {z}} \, dz = \ int _ {0} ^ {2 \ pi} {\ frac {1} {e ^ {it}}} т.е. ^ {it} \, dt = i \ int _ {0} ^ {2 \ pi} e ^ {- it} e ^ {it} \, dt \\ = i \ int _ {0} ^ {2 \ pi} dt = i ( 2 \ пи -0) = 2 \ пи я. \ Конец {выровнено}}}

Это типичный результат интегральной формулы Коши и теорема о вычетах.

Связь комплексного линейного интеграла и линейного интеграла векторного поля

Просмотр комплексных чисел как двумерных векторов, линейный интеграл комплекснозначной функции $f (z) {\ displaystyle f (z)}$ ${\ displaystyle f (z)}$ имеет действительные и комплексные части, равные линейному интегралу и интегралу потока векторного поля, соответствующего сопряженной функции. $f (z) ¯. {\ displaystyle {\ overline {f (z)}}.}$ ${\ displaystyle {\ overline {f (z)}}.}$ В частности, если $r (t) = (x (t), y (t)) {\ displaystyle \ mathbf {r } (t) = (x (t), y (t))}$ $\ mathbf {r} (t) = (x (t), y (t))$ параметризует L, а $f (z) = u (z) + iv (z) {\ displaystyle f (z) = u (z) + iv (z)}$ $f ( z) знак равно U (z) + iv (z)$ соответствует векторному полю $F (x, y) = f (x + iy) ¯ = (u (x + iy), - v (x + iy)), {\ displaystyle \ mathbf {F} (x, y) = {\ overline {f (x + iy)}} = (u (x + iy), - v (x + iy)),}$ ${\ displaystyle \ mathbf {F} (x, y) = {\ overline {е (х + iy)}} = (u (x + iy), - v (x + iy)),}$ тогда:

∫ L f (z) dz = ∫ L (u + iv) (dx + idy) = ∫ L (u, - v) ⋅ (dx, dy) + i ∫ L (u, - v) ⋅ (dy, - dx) = ∫ LF (r) ⋅ dr + i ∫ LF (r) ⋅ dr ⊥. {\ Displaystyle {\ begin {align} \ int _ {L} f (z) \, dz = \ int _ {L} (u + iv) (dx + i \, dy) \\ = \ int _ { L} (u, -v) \ cdot (dx, dy) + i \ int _ {L} (u, -v) \ cdot (dy, -dx) \\ = \ int _ {L} \ mathbf { F} (\ mathbf {r}) \ cdot d \ mathbf {r} + i \ int _ {L} \ mathbf {F} (\ mathbf {r}) \ cdot d \ mathbf {r} ^ {\ perp}. \ end {align}}}

{\ displaystyle {\ begin {align} \ int _ {L} f (z) \, dz = \ int _ {L } (u + iv) (dx + i \, dy) \\ = \ int _ {L} (u, -v) \ cdot (dx, dy) + i \ int _ {L} (u, -v) \ cdot (dy, -dx) \\ = \ int _ {L} \ mathbf {F} (\ mathbf {r}) \ cdot d \ mathbf {r} + i \ int _ {L} \ mathbf { F} (\ mathbf {r}) \ cdot d \ mathbf {r} ^ {\ perp}. \ End {align}}}

Согласно теореме Коши левый интеграл равен нулю, когда $f (z) {\ displaystyle f (z)}$ $f (z)$ является аналитическим (удовлетворяет уравнениям Коши – Римана ). Соответственно, по теореме Грина правые интегралы равны нулю, когда $F = f (z) ¯ {\ displaystyle \ mathbf {F} = {\ overline {f (z)}}}$ ${\ displaystyle \ mathbf {F} = {\ overline {f (z)}}}$ является безвихревым (curl -свободным) и несжимаемым (без дивергенции ). Фактически, уравнения Коши-Римана для $f (z) {\ displaystyle f (z)}$ $f (z)$ идентичны обращению в нуль ротора и дивергенции для F.

По теореме Грина, площадь области, окруженной гладкой замкнутой положительно ориентированной кривой $L {\ displaystyle L}$ $L$ , задается интегралом $1 2 i ∫ L z ¯ dz. {\ displaystyle \ textstyle {\ frac {1} {2i}} \ int _ {L} {\ overline {z}} \, dz.}$ ${\ displaystyle \ textstyle {\ frac {1} {2i}} \ int _ {L} {\ overline {z}} \, dz.}$ Этот факт используется, например, в доказательстве теоремы о площадях .

квантовой механики

Формулировка интеграла по путям из квантовой механики фактически относится не к интегралам по путям в этом смысле, а к функциональные интегралы, то есть интегралы по пространству путей от функции возможного пути. Однако интегралы по путям в смысле этой статьи важны в квантовой механике; например, сложное контурное интегрирование часто используется при оценке амплитуд вероятности в квантовой теории рассеяния.

Интеграл по строке

Содержание

Векторное исчисление

Линейный интеграл скалярного поля

Определение

Вывод

Линейный интеграл вектора поле

Определение

Вывод

Независимость от пути

Приложения

Обтекание кривой

Комплексный линейный интеграл

Пример

Связь комплексного линейного интеграла и линейного интеграла векторного поля

квантовой механики

См. Также

Ссылки

Внешние ссылки