Двойной пробел

редактировать

Векторное пространство линейных функций векторов, возвращающих скаляры; обобщение скалярного произведения

В математике любое векторное пространство V имеет соответствующее двойное векторное пространство (или просто двойное пространство для кратко), состоящий из всех линейных функционалов на V, вместе со структурой векторного пространства точечного сложения и скалярного умножения на константы.

Двойное пространство, как определено выше, определено для всех векторных пространств, и во избежание двусмысленности его также можно назвать алгебраическим двойственным пространством. При определении для топологического векторного пространства существует подпространство двойственного пространства, соответствующее непрерывным линейным функционалам, называемое непрерывным двойственным пространством.

Двойные векторные пространства находят применение во многих областях математики, использующих векторные пространства, например, в тензорном анализе с конечномерными векторными пространствами. Применительно к векторным пространствам функций (которые обычно являются бесконечномерными) двойственные пространства используются для описания мер, распределений и гильбертовых пространств. Следовательно, двойственное пространство является важным понятием в функциональном анализе.

Ранние термины для двойственного включают полярный Раум [Hahn 1927], сопряженное пространство, сопряженное пространство [Алаоглу 1940] и транспонертер Раум [Шаудер 1930] и [Банах 1932]. Термин двойственный появился у Бурбаки 1938.

Содержание

1 Алгебраическое двойственное пространство
- 1.1 Конечномерный случай
- 1.2 Бесконечномерный случай
- 1.3 Билинейные произведения и двойственные пространства
- 1.4 Инъекция в двойное двойное
- 1.5 Транспонирование линейного отображения
- 1.6 Факторные пространства и аннигиляторы
2 Непрерывное двойное пространство
- 2.1 Свойства
- 2.2 Топологии на двойном
- 2.3 Примеры
- 2.4 Транспонирование непрерывной линейной карты
- 2.5 Аннигиляторы
- 2.6 Дополнительные свойства
- 2.7 Двойной двойной
3 См. Также
4 Примечания
5 Ссылки
6 Библиография
7 Внешняя ссылки

Алгебраическое двойное пространство

Для любого векторного пространства $V {\ displaystyle V}$ $V$ над полем $F {\ displaystyle F}$ $F$ , (алгебраическое) двойное пространство $V ∗ {\ displaystyle V ^ {*}}$ $V^{*}$ (альтернативно обозначается $V v {\ displaystyle V ^ {v}}$ $V^{v}$ или V ′) определяется как набор всех линейных отображений φ: V → F (линейных функционалов ). Поскольку линейные отображения являются гомоморфизмами векторных пространств, двойственное пространство также иногда обозначается через Hom (V, F). Само сопряженное пространство V становится векторным пространством над F, когда оснащено сложением и скалярным умножением, удовлетворяющим:

(φ + ψ) (x) = φ (x) + ψ (x) (a φ) (x) = a (φ (Икс)) {\ Displaystyle {\ begin {выровнено} (\ varphi + \ psi) (x) = \ varphi (x) + \ psi (x) \\ (a \ varphi) (x) = a \ left (\ varphi (x) \ right) \ end {align}}}

{\begin{aligned}(\varphi +\psi)(x)=\varphi (x)+\psi (x)\\(a\varphi)(x)=a\left(\varphi (x)\right)\end{aligned}}

для всех φ и ψ ∈ V, x ∈ V и a ∈ F. Элементы алгебраического сопряженного пространства V иногда называют ковекторы или одноформные.

Спаривание функционала φ в двойственном пространстве V и элемента x из V иногда обозначается скобкой: φ (x) = [ x, φ] или φ (x) = ⟨φ, x⟩. Это спаривание определяет невырожденное билинейное отображение ⟨·, ·⟩: V × V → F, называемое естественным спариванием.

Конечномерным случаем

Если V конечномерно, то V имеет ту же размерность, что и V. Учитывая базис {e1,..., en} в V, можно построить конкретный базис в V, который называется двойная основа. Этот двойственный базис представляет собой набор {e,..., e } линейных функционалов на V, определенный соотношением

ei (c 1 e 1 + ⋯ + cnen) = ci, i = 1,…, n {\ displaystyle \ mathbf {e} ^ {i} (c_ {1} \ mathbf {e} _ {1} + \ cdots + c_ {n} \ mathbf {e} _ {n}) = c_ {i}, \ quad i = 1, \ ldots, n}

\mathbf {e} ^{i}(c_{1}\mathbf {e} _{1}+\cdots +c_{n}\mathbf {e} _{n})=c_{i},\quad i=1,\ldots,n

для любого выбора коэффициентов c i ∈ F. В частности, позволяя по очереди каждому из эти коэффициенты равны одному, а другие - нулю, дает систему уравнений

ei (ej) = δ ji {\ displaystyle \ mathbf {e} ^ {i} (\ mathbf {e} _ {j}) = \ delta _ {j} ^ {i}}

\mathbf{e}^i(\mathbf{e}_j) = \delta^{i}_{j}

где $δ ji {\ displaystyle \ delta _ {j} ^ {i}}$ $\delta^{i}_{j}$ - дельта Кронекера символ. Это свойство называется свойством биортогональности.

Например, если V равно R, пусть его базис будет выбран как {e1= (1/2, 1/2), e2= (0, 1) }. Базисные векторы не ортогональны друг другу. Тогда e и e являются одноформными (функциями, которые отображают вектор в скаляр), такие что e(e1) = 1, e(e2) = 0, e(e1) = 0 и e(e2) = 1. (Примечание: верхний индекс здесь - это индекс, а не показатель степени.) Эта система уравнений может быть выражена с использованием матричной записи как

[e 11 e 12 e 21 e 22] [e 11 e 21 e 12 e 22] = [1 0 0 1]. {\ displaystyle {\ begin {bmatrix} e_ {11} e_ {12} \\ e_ {21} e_ {22} \ end {bmatrix}} {\ begin {bmatrix} e ^ {11} e ^ {21} \ \ e ^ {12} e ^ {22} \ end {bmatrix}} = {\ begin {bmatrix} 1 0 \\ 0 1 \ end {bmatrix}}.}

{\begin{bmatrix}e_{11}e_{12}\\e_{21}e_{22}\end{bmatrix}}{\begin{bmatrix}e^{11}e^{21}\\e^{12}e^{22}\end{bmatrix}}={\begin{bmatrix}10\\01\end{bmatrix}}.

Решение этого уравнения показывает, что двойственный базис должен быть { e = (2, 0), e = (-1, 1)}. Поскольку e и e являются функционалами, их можно переписать как e (x, y) = 2x и e (x, y) = −x + y. В общем, когда V равно R, если E = (e1,..., en) представляет собой матрицу, столбцы которой являются базисными векторами, а Ê = (e,..., e ) - матрица, столбцы которой являются двойными базисными векторами, тогда

ETE ^ = I n, {\ displaystyle E ^ {T} {\ hat {E}} = I_ {n},}

E^{T}{\hat {E}}=I_{n},

где I n - единичная матрица порядка n. Свойство биортогональности этих двух базисных наборов позволяет любую точку x ∈ V представить как

x = ∑ i ⟨x, ei⟩ ei = ∑ i ⟨x, ei⟩ ei, {\ displaystyle \ mathbf {x} = \ sum _ {i} \ langle \ mathbf {x}, \ mathbf {e} ^ {i} \ rangle \ mathbf {e} _ {i} = \ sum _ {i} \ langle \ mathbf {x}, \ mathbf {e} _ {i} \ rangle \ mathbf {e} ^ {i},}

\mathbf {x} =\sum _{i}\langle \mathbf {x},\mathbf {e} ^{i}\rangle \mathbf {e} _{i}=\sum _{i}\langle \mathbf {x},\mathbf {e} _{i}\rangle \mathbf {e} ^{i},

, даже если базисные векторы не ортогональны друг другу. Строго говоря, приведенное выше утверждение имеет смысл только после того, как внутреннее произведение $⟨⋅, ⋅⟩ {\ displaystyle \ langle \ cdot, \ cdot \ rangle}$ $\langle \cdot,\cdot \rangle$ и соответствующие пары двойственности введены, как описано ниже в § Билинейные произведения и двойственные пространства.

В частности, R можно интерпретировать как пространство столбцов n действительных чисел, его двойственное пространство обычно записывается как пространство строк из n действительных чисел. Такая строка действует на R как линейный функционал посредством обычного матричного умножения. Это потому, что функционал отображает каждый n-вектор x в действительное число y. Затем, рассматривая этот функционал как матрицу M, а x, y как матрицу × 1 и матрицу 1 × 1 (тривиально, действительное число) соответственно, если Mx = y, то по соображениям размерности M должно быть размером 1 × n матрица; то есть M должен быть вектор-строкой.

Если V состоит из пространства геометрических векторов на плоскости, то кривые уровня элемента V образуют семейство параллельных прямых в V, поскольку диапазон является одномерным, так что каждая точка в диапазоне является кратной любому ненулевому элементу. Таким образом, элемент V можно интуитивно представить как определенное семейство параллельных прямых, покрывающих плоскость. Чтобы вычислить значение функционала для данного вектора, достаточно определить, на какой из линий лежит этот вектор. Неформально это «подсчитывает», сколько линий пересекает вектор. В более общем смысле, если V является векторным пространством любой размерности, то наборы уровня линейного функционала в V являются параллельными гиперплоскостями в V, и действие линейного функционала на вектор может быть визуализировано в терминах этих гиперплоскостей.

Бесконечномерный случай

Если V не конечномерный, но имеет базис eα, индексированный бесконечным множеством A, то та же конструкция, что и в конечномерном случае, дает линейно независимые элементы e (α ∈ A) двойственного пространства, но они не будут составлять базис.

Например, пространство R, элементами которого являются те последовательности действительных чисел, которые содержат только конечное число ненулевых элементов, базис которого индексируется натуральные числа N : для i ∈ N, ei- это последовательность, состоящая из всех нулей, кроме i-й позиции, которая равна 1. Двойственное пространство R (изоморфно) R, пространство всех последовательностей действительных чисел: такая последовательность (a n) применяется к элементу (x n) из R, чтобы получить число

∑ nanxn, {\ displaystyle \ sum _ {n} a_ {n} x_ {n},}

\sum _{n}a_{n}x_{n},

, которое является конечной суммой, потому что существует только конечное число ненулевых x п. Измерение для R является счетно бесконечным, тогда как R не имеет счетной основы.

Это наблюдение обобщается на любое бесконечномерное векторное пространство V над любым полем F: выбор базиса {eα: α ∈ A} отождествляет V с пространством (F) 0 функций f: A → F таких, что f α = f (α) отлична от нуля только для конечного числа α ∈ A, где такая функция f отождествляется с вектором

∑ α ∈ A f α е α {\ displaystyle \ sum _ {\ alpha \ in A} f _ {\ alpha} \ mathbf {e} _ {\ alpha}}

\sum _{\alpha \in A}f_{\alpha }\mathbf {e} _{\alpha }

в V (сумма конечна по предположению о f, и любое v ∈ V можно записать так по определению базиса).

Двойное пространство V можно затем отождествить с пространством F всех функций от A до F: линейный функционал T на V однозначно определяется значениями θ α = T ( eα) он принимает на основе V, и любая функция θ: A → F (с θ (α) = θ α) определяет линейный функционал T на V посредством

T (∑ α ∈ A f α e α) = ∑ α ∈ A f α T (e α) = ∑ α ∈ A f α θ α. {\ displaystyle T \ left (\ sum _ {\ alpha \ in A} f _ {\ alpha} \ mathbf {e} _ {\ alpha} \ right) = \ sum _ {\ alpha \ in A} f _ {\ alpha } T (e _ {\ alpha}) = \ sum _ {\ alpha \ in A} f _ {\ alpha} \ theta _ {\ alpha}.}

T\left(\sum _{\alpha \in A}f_{\alpha }\mathbf {e} _{\alpha }\right)=\sum _{\alpha \in A}f_{\alpha }T(e_{\alpha })=\sum _{\alpha \in A}f_{\alpha }\theta _{\alpha }.

Снова сумма конечна, потому что f α отличен от нуля только для конечного числа α.

Набор (F) 0 может быть идентифицирован (по существу по определению) с прямой суммой бесконечного числа копий F (рассматриваемой как 1-мерный вектор пространство над собой), индексируемое A, т. е. существуют линейные изоморфизмы

V ≅ (FA) 0 ≅ ⨁ α ∈ AF. {\ displaystyle V \ cong (F ^ {A}) _ {0} \ cong \ bigoplus _ {\ alpha \ in A} F.}

V\cong (F^{A})_{0}\cong \bigoplus _{\alpha \in A}F.

С другой стороны, F (опять же по определению), прямой продукт бесконечного числа копий F, проиндексированных A, и поэтому идентификация

V ∗ ≅ (⨁ α ∈ AF) ∗ ≅ ∏ α ∈ AF ∗ ≅ ∏ α ∈ AF ≅ FA {\ displaystyle V ^ {*} \ cong \ left (\ bigoplus _ {\ alpha \ in A} F \ right) ^ {*} \ cong \ prod _ {\ alpha \ in A} F ^ {*} \ cong \ prod _ {\ alpha \ in A} F \ cong F ^ {A}}

V^{*}\cong \left(\bigoplus _{\alpha \in A}F\right)^{*}\cong \prod _{\alpha \in A}F^{*}\cong \prod _{\alpha \in A}F\cong F^{A}

- это частный случай общего результата, связывающего прямые суммы (модулей) с прямыми произведениями.

Если базис бесконечен, то алгебраическое двойственное пространство всегда имеет большую размерность (как кардинальное число ), чем исходное векторное пространство. Это контрастирует со случаем непрерывного двойственного пространства, обсуждаемого ниже, которое может быть изоморфным исходному векторному пространству, даже если последнее является бесконечномерным.

Билинейные произведения и двойственные пространства

Если V конечномерно, то V изоморфно V. Но, как правило, нет естественного изоморфизма между этими двумя пространствами. Любая билинейная форма ⟨·, ·⟩ на V дает отображение V в двойственное пространство через

v ↦ ⟨v, ⋅⟩ {\ displaystyle v \ mapsto \ langle v, \ cdot \ rangle }

v\mapsto \langle v, \cdot\rangle

где правая часть определяется как функционал на V, переводящий каждый w ∈ V в ⟨v, w⟩. Другими словами, билинейная форма определяет линейное отображение

Φ ⟨⋅, ⋅⟩: V → V ∗ {\ displaystyle \ Phi _ {\ langle \ cdot, \ cdot \ rangle}: V \ to V ^ {* }}

\Phi_{\langle\cdot,\cdot\rangle} : V\to V^*

определяется как

[Φ ⟨⋅, ⋅⟩ (v), w] = ⟨v, w⟩. {\ displaystyle \ left [\ Phi _ {\ langle \ cdot, \ cdot \ rangle} (v), w \ right] = \ langle v, w \ rangle.}

\left[\Phi _{\langle \cdot,\cdot \rangle }(v),w\right]=\langle v,w\rangle.

Если билинейная форма невырожденная, то это изоморфизм на подпространство в V. Если V конечномерно, то это изоморфизм на все V. Наоборот, любой изоморфизм $Φ {\ displaystyle \ Phi}$ $\Phi$ из V в подпространство в V (соответственно, все из V, если V конечномерно) определяет уникальную невырожденную билинейную форму $⟨⋅, ⋅⟩ Φ {\ displaystyle \ langle \ cdot, \ cdot \ rangle _ {\ Phi}}$ $\langle \cdot,\cdot \rangle _{\Phi }$ на V по

⟨v, w⟩ Φ = (Φ (v)) (w) = [Φ (v), w]. {\ displaystyle \ langle v, w \ rangle _ {\ Phi} = (\ Phi (v)) (w) = [\ Phi (v), w]. \,}

\langle v,w\rangle _{\Phi }=(\Phi (v))(w)=[\Phi (v),w].\,

Таким образом, существует однозначный - одно соответствие между изоморфизмами V подпространству (соответственно всем) V и невырожденным билинейным формам на V.

Если векторное пространство V находится над комплексным полем , то иногда более естественно рассматривать полуторалинейные формы вместо билинейных. В этом случае заданная полуторалинейная форма ⟨·, ·⟩ определяет изоморфизм V с комплексно сопряженным двойственным пространством

Φ ⟨⋅, ⋅⟩: V → V ∗ ¯. {\ displaystyle \ Phi _ {\ langle \ cdot, \ cdot \ rangle}: V \ to {\ overline {V ^ {*}}}.}

\Phi _{\langle \cdot,\cdot \rangle }:V\to {\overline {V^{*}}}.

Сопряженное пространство V можно отождествить с множеством всех аддитивных комплекснозначные функционалы f: V → C такие, что

f (α v) = α ¯ f (v). {\ displaystyle f (\ alpha v) = {\ overline {\ alpha}} f (v).}

f(\alpha v) = \overline{\alpha}f(v).

Инъекция в двойную двойную

Существует естественная гомоморфизм $Ψ {\ displaystyle \ Psi}$ $\Psi$ из $V {\ displaystyle V}$ $V$ в двойное двойное $V ∗ ∗ = { Φ: V ∗ → F: Φ linear} {\ displaystyle V ^ {**} = \ {\ Phi: V ^ {*} \ to F: \ Phi \ \ mathrm {linear} \}}$ $V^{**}=\{\Phi :V^{*}\to F:\Phi \ \mathrm {linear} \}$ , определяемый формулой $(Ψ (v)) (φ) = φ (v) {\ displaystyle (\ Psi (v)) (\ varphi) = \ varphi (v)}$ $(\Psi (v))(\varphi)=\varphi (v)$ для всех $v ∈ V, φ ∈ V ∗ {\ displaystyle v \ in V, \ varphi \ in V ^ {*}}$ $v\in V,\varphi \in V^{*}$ . Другими словами, если $evv: V ∗ → F {\ displaystyle \ mathrm {ev} _ {v}: V ^ {*} \ to F}$ $\mathrm {ev} _{v}:V^{*}\to F$ - это карта оценки, определенная $φ ↦ φ (v) {\ displaystyle \ varphi \ mapsto \ varphi (v)}$ $\varphi \mapsto \varphi (v)$ , затем $Ψ: V → V ∗ ∗ {\ displaystyle \ Psi: V \ to V ^ { **}}$ $\Psi :V\to V^{**}$ определяется как карта $v ↦ evv {\ displaystyle v \ mapsto \ mathrm {ev} _ {v}}$ $v\mapsto \mathrm {ev} _{v}$ . Эта карта $Ψ {\ displaystyle \ Psi}$ $\Psi$ всегда инъективная ; это изоморфизм тогда и только тогда, когда $V {\ displaystyle V}$ $V$ является конечномерным. В самом деле, изоморфизм конечномерного векторного пространства с его двойным двойным пространством является архетипическим примером естественного изоморфизма. Бесконечномерные гильбертовы пространства не являются контрпримером к этому, поскольку они изоморфны своим непрерывным двойникам, а не своим алгебраическим двойникам.

Транспонирование линейной карты

Если f: V → W является линейной картой, то транспонирует (или двойное) f: W → V определяется выражением

f ∗ (φ) = φ ∘ f {\ displaystyle f ^ {*} (\ varphi) = \ varphi \ circ f \,}

f^*(\varphi) = \varphi \circ f \,

для каждого φ ∈ W. Полученный функционал f (φ) в V называется откатом отображения φ вдоль f.

Для всех φ ∈ W и v ∈ V выполняется следующее тождество:

[f ∗ (φ), v] = [φ, f (v)], {\ displaystyle [f ^ {* } (\ varphi), \, v] = [\ varphi, \, f (v)],}

[f^*(\varphi),\, v] = [\varphi,\, f(v)],

где скобка [·, ·] слева - это естественное спаривание V с его двойственным пространством, а что справа - естественное спаривание W со своим двойником. Это тождество характеризует транспонирование и формально аналогично определению сопряженного.

. Присваивание f ↦ f создает инъективное линейное отображение между пространством линейных операторов из V в W и пространство линейных операторов из W в V; этот гомоморфизм является изоморфизмом тогда и только тогда, когда W конечномерно. Если V = W, то пространство линейных отображений на самом деле является алгеброй при композиции отображений, и тогда присвоение является антигомоморфизмом алгебр, что означает, что ( fg) = gf. На языке теории категорий, взятие двойственного векторных пространств и транспонирование линейных отображений, следовательно, является контравариантным функтором из категории векторных пространств над F в себя. Можно отождествить (f) с f, используя естественную инъекцию в двойное двойственное.

Если линейное отображение f представлено матрицей A относительно двух оснований V и W, то f представлено матрицей A транспонирования относительно к двойственным базисам W и V, отсюда и название. В качестве альтернативы, поскольку f представлен A, действующим слева на векторах-столбцах, f представлен той же самой матрицей, действующей справа на векторах-строках. Эти точки зрения связаны каноническим внутренним произведением на R, которое идентифицирует пространство векторов-столбцов с двойным пространством векторов-строк.

Факторпространства и аннигиляторы

Пусть S будет подмножеством V. аннигилятор S в V, обозначенный здесь S, является совокупностью линейных функционалов f ∈ V таких, что [f, s] = 0 для всех s ∈ S. То есть S состоит из всех линейных функционалов f: V → F таких, что ограничение на S обращается в нуль: f | S = 0. В конечномерных векторных пространствах аннигилятор двойственен (изоморфен) ортогональному дополнению .

Аннигилятор подмножества сам является векторным пространством. Аннигилятором нулевого вектора является все двойственное пространство: ${0} 0 = V ∗ {\ displaystyle \ {0 \} ^ {0} = V ^ {*}}$ $\{0\}^{0}=V^{*}$ , а аннигилятор всего пространства - это просто нулевой ковектор: $V 0 = {0} ⊆ V ∗ {\ displaystyle V ^ {0} = \ {0 \} \ substeq V ^ {*}}$ $V^{0}=\{0\}\subseteq V^{*}$ . Кроме того, назначение аннулятора подмножеству V обращает включения, так что если S ⊆ T ⊆ V, то

0 ⊆ T 0 ⊆ S 0 ⊆ V ∗. {\ displaystyle 0 \ substeq T ^ {0} \ substeq S ^ {0} \ substeq V ^ {*}.}

0\subseteq T^{0}\subseteq S^{0}\subseteq V^{*}.

Если A и B - два подмножества V, то

(A ∩ B) 0 ⊇ A 0 + B 0, {\ displaystyle (A \ cap B) ^ {0} \ supseteq A ^ {0} + B ^ {0},}

(A\cap B)^{0}\supseteq A^{0}+B^{0},

и равенство выполняется при условии, что V конечномерно. Если A i - любое семейство подмножеств V, индексированных i, принадлежащих некоторому набору индексов I, то

(⋃ i ∈ I A i) 0 = ⋂ i ∈ I A i 0. {\ displaystyle \ left (\ bigcup _ {i \ in I} A_ {i} \ right) ^ {0} = \ bigcap _ {i \ in I} A_ {i} ^ {0}.}

\left(\bigcup _{i\in I}A_{i}\right)^{0}=\bigcap _{i\in I}A_{i}^{0}.

In в частности, если A и B подпространства в V, то

(A + B) 0 = A 0 ∩ B 0. {\ displaystyle (A + B) ^ {0} = A ^ {0} \ cap B ^ {0}.}

(A+B)^{0}=A^{0}\cap B^{0}.

Если V конечномерно, а W является векторным подпространством , то

W 00 = W {\ displaystyle W ^ {00} = W}

W^{00}=W

после отождествления W с его изображением во втором двойственном пространстве при изоморфизме двойной двойственности V ≈ V. В частности, формирование аннигилятора - это Связность Галуа на решетке подмножеств конечномерного векторного пространства.

Если W является подпространством V, то фактор-пространство V / W является векторным пространством само по себе и, следовательно, имеет двойственное. Согласно первой теореме об изоморфизме , функционал f: V → F факторизуется через V / W тогда и только тогда, когда W находится в ядре функции f. Таким образом, существует изоморфизм

(V / W) ∗ ≅ W 0. {\ displaystyle (V / W) ^ {*} \ cong W ^ {0}.}

(V/W)^{*}\cong W^{0}.

В частности, если V является прямой суммой двух подпространств A и B, то V является прямой суммой A и B.

Непрерывное двойное пространство

При работе с топологическими векторными пространствами, непрерывные линейные функционалы из пространства в базовое поле $F = C {\ displaystyle \ mathbb {F} = \ mathbb {C}}$ $\mathbb {F} =\mathbb {C}$ (или $R {\ displaystyle \ mathbb {R}}$ $\mathbb {R}$ ) особенно важны. Это дает начало понятию «непрерывного двойственного пространства» или «топологического двойственного пространства», которое является линейным подпространством алгебраического двойственного пространства $V ∗ {\ displaystyle V ^ {*}}$ $V^{*}$ , обозначаемого Автор $V ′ {\ displaystyle V '}$ $V'$ . Для любого конечномерного нормированного векторного пространства или топологического векторного пространства, такого как евклидово n-пространство, непрерывное двойственное и алгебраическое двойственное совпадают. Однако это неверно для любого бесконечномерного нормированного пространства, как показано на примере разрывных линейных отображений. Тем не менее, в теории топологических векторных пространств термины «непрерывное двойственное пространство» и «топологическое двойственное пространство» часто заменяются на «двойственное пространство».

Для топологического векторного пространства $V {\ displaystyle V}$ $V$ его непрерывное двойственное пространство, или топологическое двойное пространство, или просто двойное пространство (в смысле теории топологических векторных пространств) $V ′ {\ displaystyle V '}$ $V'$ определяется как пространство всех непрерывных линейных функционалов $φ: V → F {\ displaystyle \ varphi: V \ to {\ mathbb {F}}}$ $\varphi:V\to{\mathbb F}$ .

Свойства

Если X является Хаусдорфом топологическим векторным пространством (TVS), то непрерывное двойственное пространство X идентичен непрерывному двойному пространству завершения X.

Топологии на двойном

Существует стандартная конструкция для введения топологии на непрерывном двойственном $V '{\ displaystyle V'}$ $V'$ топологического векторного пространства $V {\ displaystyle V}$ $V$ . Исправьте коллекцию $A {\ displaystyle {\ mathcal {A}}}$ ${\mathcal {A}}$ из ограниченных подмножеств из $V {\ displaystyle V}$ $V$ . Это дает топологию на $V {\ displaystyle V}$ $V$ равномерной сходимости на множествах из $A, {\ displaystyle {\ mathcal {A}},}$ ${\mathcal {A}},$ или что то же самое, топология, порожденная полунормами вида

‖ φ ‖ A = sup x ∈ A | φ (x) |, {\ displaystyle \ | \ varphi \ | _ {A} = \ sup _ {x \ in A} | \ varphi (x) |,}

\|\varphi \|_{A}=\sup _{x\in A}|\varphi (x)|,

где $φ {\ displaystyle \ varphi}$ $\varphi$ - это непрерывный линейный функционал на $V {\ displaystyle V}$ $V$ , а $A {\ displaystyle A}$ $A$ работает над классом $A. {\ displaystyle {\ mathcal {A}}.}$ ${\mathcal {A}}.$

Это означает, что сеть функционалов $φ i {\ displaystyle \ varphi _ {i}}$ $\varphi _{i}$ стремится к функциональному $φ {\ displaystyle \ varphi}$ $\varphi$ в $V ′ {\ displaystyle V '}$ $V'$ тогда и только тогда, когда

для всех A ∈ A ‖ φ i - φ ‖ A = sup x ∈ A | φ i (x) - φ (x) | ⟶ я → ∞ 0. {\ displaystyle {\ text {для всех}} A \ in {\ mathcal {A}} \ qquad \ | \ varphi _ {i} - \ varphi \ | _ {A} = \ sup _ {x \ in A} | \ varphi _ {i} (x) - \ varphi (x) | {\ underset {i \ to \ infty} {\ longrightarrow}} 0.}

{\text{ for all }}A\in {\mathcal {A}}\qquad \|\varphi _{i}-\varphi \|_{A}=\sup _{x\in A}|\varphi _{i}(x)-\varphi (x)|{\underset {i\to \infty }{\longrightarrow }}0.

Обычно (но не обязательно) класс $A {\ displaystyle {\ mathcal {A}}}$ ${\mathcal {A}}$ должен удовлетворять следующим условиям:

Каждая точка $x {\ displaystyle x}$ $x$ из $V {\ displaystyle V}$ $V$ принадлежит некоторому набору $A ∈ A {\ displaystyle A \ in {\ mathcal {A}}}$ $A\in {\mathcal {A}}$ :

для всех x ∈ V в нем существует некоторый A ∈ A такой, что x ∈ A. {\ displaystyle {\ text {для всех}} x \ in V \ quad {\ text {существует несколько}} A \ in {\ mathcal {A}} \ quad {\ text {такое, что}} x \ in A.}

{\text{ for all }}x\in V\quad {\text{ there exists some }}A\in {\mathcal {A}}\quad {\text{ such that }}x\in A.

Каждые два набора $A ∈ A {\ displaystyle A \ in {\ mathcal {A}}}$ $A\in {\mathcal {A}}$ и $B ∈ A {\ displaystyle B \ in {\ mathcal {A}}}$ $B\in {\mathcal {A}}$ содержатся в некотором наборе $C ∈ A {\ displaystyle C \ in {\ mathcal {A}}}$ $C\in {\mathcal {A}}$ :

для всех A, B ∈ A существует некоторый ∈ A такое, что A ∪ B ⊆ C. {\ displaystyle {\ text {для всех}} A, B \ in {\ mathcal {A}} \ quad {\ text {там есть некоторые}} \ in {\ mathcal {A}} \ quad {\ text {такие что}} A \ cup B \ substeq C.}

{\text{ for all }}A,B\in {\mathcal {A}}\quad {\text{ there exists some }}\in {\mathcal {A}}\quad {\text{ such that }}A\cup B\subseteq C.

$A {\ displaystyle {\ mathcal {A}}}$ ${\mathcal {A}}$ замыкается при операции умножения на скаляры:

для всех A ∈ A и все λ ∈ F такие, что λ ⋅ A ∈ A. {\ displaystyle {\ text {для всех}} A \ in {\ mathcal {A}} \ quad {\ text {and all}} \ lambda \ in {\ mathbb {F}} \ quad {\ text {такой, что }} \ lambda \ cdot A \ in {\ mathcal {A}}.}

{\text{ for all }}A\in {\mathcal {A}}\quad {\text{ and all }}\lambda \in {\mathbb {F} }\quad {\text{ such that }}\lambda \cdot A\in {\mathcal {A}}.

Если эти требования выполнены, то соответствующая топология на $V ′ {\ displaystyle V '}$ $V'$ будет Хаусдорфовой и множества

UA = {φ ∈ V ′: ‖ φ ‖ A < 1 }, for A ∈ A {\displaystyle U_{A}~=~\left\{\varphi \in V'~:~\quad \|\varphi \|_{A}<1\right\},\qquad {\text{ for }}A\in {\mathcal {A}}}

U_{A}~=~\left\{\varphi \in V'~:~\quad \|\varphi \|_{A}<1\right\},\qquad {\text{ for }}A\in {\mathcal {A}}

образуют его локальную базу.

Вот три самых важных особых случая.

сильная топология на $V ′ {\ displaystyle V '}$ $V'$ - это топология равномерной сходимости на ограниченных подмножествах в $V {\ displaystyle V}$ $V$ (так что здесь $A {\ displaystyle {\ mathcal {A}}}$ ${\mathcal {A}}$ может быть выбран как класс всех ограниченных подмножеств в $V {\ displaystyle V}$ $V$ ).

Если $V {\ displaystyle V}$ $V$ - это нормированное векторное пространство (например, банахово пространство или Гильбертово пространство ), то сильная топология на $V ′ {\ displaystyle V '}$ $V'$ нормирована (фактически, это банахово пространство, если поле скаляров полно), с норма

‖ φ ‖ знак равно sup ‖ x ‖ ≤ 1 | φ (x) |, {\ displaystyle \ | \ varphi \ | = \ sup _ {\ | x \ | \ leq 1} | \ varphi (x) |.}

\|\varphi \|=\sup _{\|x\|\leq 1}|\varphi (x)|.

Стереотипная топология на $V ′ {\ displaystyle V '}$ $V'$ - это топология равномерной сходимости на полностью ограниченных множествах в $V {\ displaystyle V}$ $V$ (поэтому здесь $A {\ displaystyle {\ mathcal {A}}}$ ${\mathcal {A}}$ может быть выбран как класс для всех y ограниченные подмножества в $V {\ displaystyle V}$ $V$ ).

слабая топология на $V ′ {\ displaystyle V '}$ $V'$ - это топология равномерной сходимости на конечные подмножества в $V {\ displaystyle V}$ $V$ (поэтому здесь $A {\ displaystyle {\ mathcal {A}}}$ ${\mathcal {A}}$ может быть выбран как класс всех конечные подмножества в $V {\ displaystyle V}$ $V$ ).

Каждый из этих трех вариантов топологии на $V ′ {\ displaystyle V '}$ $V'$ приводит к варианту свойства рефлексивности для топологических векторных пространств:

Если $V ′ {\ displaystyle V '}$ $V'$ наделен сильной топологией, то соответствующее понятие рефлексивности является стандартный: рефлексивные в этом смысле пространства просто называются рефлексивными.

Если $V ′ {\ displaystyle V '}$ $V'$ наделен стереотипной дуальной топологией, то соответствующая рефлексивность представлена в теория стереотипных пространств : рефлексивные в этом смысле пространства называются стереотипными.

Если $V ′ {\ di splaystyle V '}$ $V'$ наделен слабой топологией, тогда соответствующая рефлексивность представлена в теории дуальных пар : рефлексивные в этом смысле пространства произвольны (Хаусдорф) локально выпуклые пространства со слабой топологией.

Примеры

Пусть 1 < p < ∞ be a real number and consider the Banach space ℓ всех последовательностей a= (a n) для которого

‖ a ‖ p = (∑ n = 0 ∞ | а п | p) 1 p < ∞. {\displaystyle \|\mathbf {a} \|_{p}=\left(\sum _{n=0}^{\infty }|a_{n}|^{p}\right)^{\frac {1}{p}}<\infty.}

\|\mathbf {a} \|_{p}=\left(\sum _{n=0}^{\infty }|a_{n}|^{p}\right)^{\frac {1}{p}}<\infty.

Определим число q как 1 / p + 1 / q = 1. Тогда непрерывный двойственный элемент ℓ естественным образом отождествляется с ℓ: для данного элемента φ ∈ (ℓ) ′ соответствующий элемент равен последовательность (φ (en)), где enобозначает последовательность, у которой n-й член равен 1, а все остальные равны нулю. И наоборот, для элемента a = (a n) ∈ ℓ соответствующий непрерывный линейный функционал φ на ℓ определяется как

ϕ (b) = ∑ nanbn {\ displaystyle \ phi (\ mathbf {b}) = \ sum _ {n} a_ {n} b_ {n}}

\phi (\mathbf {b})=\sum _{n}a_{n}b_{n}

для всех b = (b n) ∈ ℓ (см. неравенство Гёльдера ).

Подобным образом непрерывный двойственный элемент естественным образом отождествляется с (пространством ограниченных последовательностей). Кроме того, непрерывные двойники банаховых пространств c (состоящие из всех сходящихся последовательностей с нормой супремума ) и c 0 (сходящиеся к нулю последовательности) оба естественно отождествляются с ℓ.

Согласно теореме о представлении Рисса, непрерывное двойственное гильбертово пространство снова является гильбертовым пространством, которое антиизоморфно исходному пространству. Это приводит к обозначению бюстгальтера, используемому физиками в математической формулировке квантовой механики.

Согласно теореме о представлении Рисса – Маркова – Какутани, непрерывная двойственная некоторых пространств непрерывных функций можно описать с помощью мер.

Транспонирование непрерывного линейного отображения

Если T: V → W - непрерывное линейное отображение между двумя топологическими векторными пространствами, то (непрерывное) транспонирование T ′: W ′ → V ′ является определяется той же формулой, что и раньше:

T ′ (φ) = φ ∘ T, φ ∈ W ′. {\ displaystyle T '(\ varphi) = \ varphi \ circ T, \ quad \ varphi \ in W'.}

T'(\varphi)=\varphi \circ T,\quad \varphi \in W'.

Результирующий функционал T '(φ) находится в V'. Присвоение T → T ′ создает линейное отображение между пространством непрерывных линейных отображений из V в W и пространством линейных отображений из W ′ в V ′. Когда T и U - составные непрерывные линейные отображения, то

(U ∘ T) ′ = T ′ ∘ U ′. {\ displaystyle (U \ circ T) '= T' \ circ U '.}

(U\circ T)'=T'\circ U'.

Когда V и W нормированные пространства, норма транспонирования в L (W', V ') равна норме T в L (V, W). Некоторые свойства транспонирования зависят от теоремы Хана – Банаха. Например, ограниченное линейное отображение T имеет плотный диапазон тогда и только тогда, когда транспонированное T ′ инъективно.

Когда T является компактным линейным отображением между двумя банаховыми пространствами V и W, то транспонирование T 'компактно. Это можно доказать с помощью теоремы Арзела – Асколи.

. Когда V - гильбертово пространство, существует антилинейный изоморфизм i V из V на его непрерывное двойственное V ′. Для любого ограниченного линейного отображения T на V операторы транспонирования и присоединенного связаны соотношением

i V ∘ T ∗ = T ′ ∘ i V. {\ displaystyle i_ {V} \ circ T ^ {*} = T '\ circ i_ {V}.}

i_{V}\circ T^{*}=T'\circ i_{V}.

Когда T - непрерывное линейное отображение между двумя топологическими векторными пространствами V и W, то транспонированный T ′ равен непрерывна, когда W ′ и V ′ оснащены «совместимыми» топологиями: например, когда для X = V и X = W, оба двойственных X ′ имеют сильную топологию β (X ′, X) равномерная сходимость на ограниченных множествах X, либо оба имеют ∗ -слабую топологию σ (X ′, X) поточечной сходимости на X. Транспонирование T ′ непрерывно от β (W ′, W) к β (V ′, V) или от σ (W ′, W) к σ (V ′, V).

Аннигиляторы

Предположим, что W - замкнутое линейное подпространство нормированного пространства V, и рассмотрим аннигилятор W в V ′,

W ⊥ = {φ ∈ V ′: W ⊆ ker ⁡ φ}. {\ displaystyle W ^ {\ perp} = \ {\ varphi \ in V ': W \ substeq \ ker \ varphi \}.}

W^{\perp }=\{\varphi \in V':W\subseteq \ker \varphi \}.

Тогда двойственное частное V / W можно отождествить с W, и двойственный к W может быть отождествлен с фактором V '/ W. Действительно, пусть P обозначает каноническую сюръекцию из V на фактор V / W; тогда транспонирование P ′ является изометрическим изоморфизмом из (V / W) ′ в V ′ с диапазоном, равным W. Если j обозначает отображение инъекции из W в V, то ядро транспонированного j ′ является аннулятором W:

ker ⁡ (j ') = W ⊥ {\ displaystyle \ ker (j') = W ^ {\ perp}}

\ker (j') = W^\perp

и из теоремы Хана – Банаха следует, что j ′ индуцирует изометрический изоморфизм V ′ / W → W ′.

Дополнительные свойства

Если двойственное к нормированному пространству V отделимо, то само пространство V также. Обратное неверно: например, пространство сепарабельно, а его двойственное - нет.

Двойной двойственный

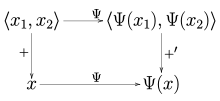Это естественное преобразование сложения векторов из векторного пространства в его двойное двойственное. ⟨X 1, x 2 ⟩ обозначает упорядоченную пару двух векторов. Сложение + отправляет x 1 и x 2 в x 1 + x 2. The addition +′ induced by the transformation can be defined as (Ψ(x1) +′ Ψ(x2))(φ) = φ(x1+ x2) = φ(x) for any φ in the dual space.

In analogy with the case of the algebraic double dual, there is always a naturally defined continuous linear operator Ψ : V → V′′ from a normed space V into its continuous double dual V′′, defined by

Ψ ( x) ( φ) = φ ( x), x ∈ V, φ ∈ V ′. {\displaystyle \Psi (x)(\varphi)=\varphi (x),\quad x\in V,\ \varphi \in V'.}

\Psi (x)(\varphi)=\varphi (x),\quad x\in V,\ \varphi \in V'.

As a consequence of the Hahn–Banach theorem, this map is in fact an isometry, meaning ‖ Ψ(x) ‖ = ‖ x ‖ for all x ∈ V. Normed spaces for which the map Ψ is a bijection are called reflexive.

When V is a topological vector space then Ψ(x) can still be defined by the same formula, for every x ∈ V, however several difficulties arise. First, when V is not locally convex, the continuous dual may be equal to { 0 } and the map Ψ trivial. However, if V is Hausdorff and locally convex, the map Ψ is injective from V to the algebraic dual V′ of the continuous dual, again as a consequence of the Hahn–Banach theorem.

Second, even in the locally convex setting, several natural vector space topologies can be defined on the continuous dual V′, so that the continuous double dual V′′ is not uniquely defined as a set. Saying that Ψ maps from V to V′′, or in other words, that Ψ(x) is continuous on V′ for every x ∈ V, is a reasonable minimal requirement on the topology of V′, namely that the evaluation mappings

φ ∈ V ′ ↦ φ ( x), x ∈ V, {\displaystyle \varphi \in V'\mapsto \varphi (x),\quad x\in V,}

\varphi \in V'\mapsto \varphi (x),\quad x\in V,

be continuous for the chosen topology on V′. Further, there is still a choice of a topology on V′′, and continuity of Ψ depends upon this choice. As a consequence, defining reflexivity in this framework is more involved than in the normed case.