Вероятностная мера

Мера общего значения 1, обобщающая распределения вероятностей Во многих случаях статистическая физика использует вероятностные меры, но не все меры, которые она использует, являются вероятностными.

В математике вероятность мера - это функция с действительным знаком, определенная для набора событий в вероятностном пространстве, которая удовлетворяет свойствам мера, таким как счетная аддитивность. Разница между вероятностной мерой и более общим понятием меры (которое включает такие понятия, как площадь или объем ) заключается в том, что вероятностная мера должна присваивать значение 1 всему вероятностному пространству.

Интуитивно свойство аддитивности говорит, что вероятность, присвоенная объединению двух непересекающихся событий мерой, должна быть суммой вероятностей событий, например значение, присвоенное «1 или 2» при броске кубика, должно быть суммой значений, присвоенных «1» и «2».

Вероятностные меры имеют приложения в различных областях, от физики до финансов и биологии.

• 1 Определение
• 2 Примеры приложений
• 3 См. Также
• 4 Ссылки
• 5 Дополнительная литература
• 6 Внешние ссылки

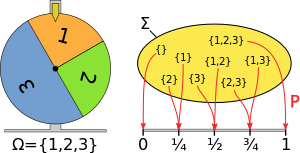Вероятностная мера, отображающая вероятностное пространство для $2\; 3\; \{\backslash \; displaystyle\; 2\; ^\; \{3\}\}$событий в единичном интервале.

Требования к функции μ быть вероятностной мерой на вероятностное пространство таковы:

• μ должен возвращать результаты в единичном интервале [0, 1], возвращая 0 для пустого набора и 1 для всего пространства.

• μ должен удовлетворять свойство счетной аддитивности, которое для всех счетных коллекций $\{E\; i\}\; \{\backslash \; displaystyle\; \backslash \; \{E\_\; \{i\}\; \backslash \}\}$попарных непересекающихся множеств :

$\mu \; (\bigcup \; i\; \in \; IE\; i)\; =\; \sum \; i\; \in \; I\; \mu \; (E\; i).\; \{\backslash \; displaystyle\; \backslash \; mu\; \{\backslash \; Bigl\; (\}\; \backslash \; bigcup\; \_\; \{i\; \backslash \; in\; I\}\; E\_\; \{i\}\; \{\backslash \; Bigr)\}\; =\; \backslash \; sum\; \_\; \{i\; \backslash \; in\; I\}\; \backslash \; mu\; (E\_\; \{i\}).\}$

Например, учитывая три элемента 1, 2 и 3 с вероятностями 1/4, 1/4 и 1/2, значение, присвоенное {1, 3}, равно 1/4 + 1/2 = 3/4, как в диаграмма справа.

условная вероятность, основанная на пересечении событий, определяемых как:

$\mu \; (B\; \mid \; A)\; =\; \mu \; (A\; \cap \; B)\; \mu \; (A).\; \{\backslash \; displaystyle\; \backslash \; mu\; (B\; \backslash \; mid\; A)\; =\; \{\backslash \; frac\; \{\backslash \; mu\; (A\; \backslash \; cap\; B)\}\; \{\backslash \; mu\; (A)\}\}.\}$

удовлетворяет требованиям вероятностной меры, пока $\mu \; (A)\; \{\backslash \; displaystyle\; \backslash \; mu\; (A)\}$не равно нулю.

Вероятностные меры отличаются от более общего понятия нечетких мер, в котором есть Нет требования, чтобы сумма нечетких значений составляла 1, а аддитивное свойство заменялось отношением порядка, основанным на включении множества.

Рыночные меры, которые присваивают вероятности финансовому рынку пробелы, основанные на реальных движениях рынка, являются примерами вероятностных показателей, которые представляют интерес в математических финансах, например в ценообразовании производных финансовых инструментов. Например, нейтральная к риску мера является вероятностной мерой, которая предполагает, что текущая стоимость активов является ожидаемой стоимостью будущей выплаты, принятой в отношении той же нейтральной к риску меры ( т.е. рассчитано с использованием соответствующей функции плотности нейтрального риска), и дисконтировано по безрисковой ставке. Если существует уникальная вероятностная мера, которая должна использоваться для определения цены активов на рынке, то рынок называется полным рынком.

Не все меры, которые интуитивно представляют шанс или вероятность, являются вероятностными мерами. Например, хотя фундаментальная концепция системы в статистической механике - это пространство мер, такие меры не всегда являются вероятностными. В общем, в статистической физике, если мы рассмотрим предложения вида «вероятность того, что система S принимает состояние A равно p», геометрия системы не всегда приводит к определению вероятностной меры при сравнении, хотя это может происходить в случае систем только с одной степенью свободы.

Вероятностные меры также используются в математической биологии. Например, в сравнительном анализе последовательностей мера вероятности может быть определена для вероятности того, что вариант может быть допустимым для аминокислоты в последовательности.

Ультрафильтры могут следует понимать как $\{0,\; 1\}\; \{\backslash \; displaystyle\; \backslash \; \{0,1\; \backslash \}\}$-значные вероятностные меры, позволяющие проводить множество интуитивных доказательств, основанных на измерениях. Например, теорема Хиндмана может быть доказана путем дальнейшего исследования этих мер, и их свертки в частности.

• Мера Бореля
• Нечеткая мера
• Мера Хаара
• Мера Мартингейла
• Мера Лебега

• Биллингсли, Патрик (1995). Вероятность и мера. Джон Вили. ISBN 0-471-00710-2.
• Эш, Роберт Б.; Doléans-Dade, Кэтрин А. (1999). Теория вероятностей и меры. Академическая пресса. ISBN 0-12-065202-1.

• СМИ, связанные с Мера вероятности на Wikimedia Commons