Возведение в степень

Математическая операция

Различные Графики y = b для оснований b: основание 10, основание e, основание 2, основание 1/2. Каждое кривая проходит через точку (0, 1), потому что любое ненулевое число, возведенное в степень 0, равно 1. При x = 1 значение y равно основанию, поскольку любое число, возведенное в степень 1, является самим числом.

Возведение в степень - это математическая операция, записанная как b, включающая два числа, основание b и показатель степени или степени n, и произносится как как "б в степени п". Когда n является положительным целым числом, возведение в степень соответствует повторному умножению основания: то есть b произведением умножения n оснований:

$bn\; =\; b\; \times \; \cdots \; \times \; b\; ⏟\; n\; раз.\; \{\backslash \; displaystyle\; b\; ^\; \{n\}\; =\; \backslash \; underbrace\; \{b\; \backslash \; times\; \backslash \; dots\; \backslash \; times\; b\}\; \_\; \{n\; \backslash ,\; \{\backslash \; textrm\; \{times\}\}\}.\}$

Показатель обычно отображается как верхний индекс справа от основания. В этом случае b называется «b в степени n», «b в степени n», «n-й степени b», «b в n-й степени» или наиболее кратко как «б в п».

Один имеет b = b, и для любых натуральных чисел m и n b one b = b. Чтобы распространить это свойство на неположительные целые показатели степени, b определяется как 1, а b (с n положительным целым числом и b не равным нулю) определяется как 1 / b. В частности, b равно 1 / b, , обратному б.

Определение возведения в степень может быть расширено, чтобы разрешить любой действительный или комплексный показатель степени. Возведение в степень с помощью целочисленных показателей также может быть определено для широкого круга алгебраических структур, включая матрицы.

Возведение в степень широко используется во многих областях, включая экономику, биологию, химия, физика и информатика, с такими приложениями, как сложный процент, рост населения, кинетика химической реакции, волновое поведение и криптография с открытым ключом.

• 1 История записи
• 2 Терминология
• 3 Целочисленные
  • 3.1 Положительные показатели
  • 3.2 Нулевые показатели
  • 3.3 Отрицательные показатели
  • 3.4 Тождества и свойства
  • 3.5 Степени суммы
  • 3.6 Комбинаторная интерпретация
  • 3.7 Частные основания
    • 3.7.1 Полномочия десять
    • 3.7.2 Степень двойки
    • 3.7.3 Степень единицы
    • 3.7.4 Степень нуля
    • 3.7.5 Степень отрицательной единицы
  • 3.8 Большо ©
  • 3.9 Степенные функции
  • 3.10 Список степеней целых показателей чисел
• 4 R Real Lim 5.2 Показатели с положительной действительной базой
  • 6.1 Определение ряда
  • 6.2 Определение предела
  • 6.3 Периодичность
  • 6.4 Примеры
• 7 Степени комплексных чисел
  • 7.1 Комплексные показатели с комплексным основанием
  • 7.2 Комплексные корни из единицы
  • 7.3 Корни произвольных комплексных чисел
  • 7.4 Вычисление комплексных степеней
  • 7.5 Несостоятельность тождеств мощности и логарифма
• 8 Обобщения
  • 8.1 Моноиды
  • 8.2 Матрицы и линейные операторы
  • 8.3 Конечные поля
  • 8.4 В абстрактной алгебре
  • 8.5 Дополнительные числа
  • 8.6 В теории категорий
  • 8.7 Кардинальных и порядковых чисел
• 9 Повторное возведение в степень
• 10 Пределы степеней
• 11 Эффективное вычисление с целыми показателями
• 12 Экспоненциальная запись для имен функций
• 13 На языке программирования возраст
• 14 См. также
• 15 Примечания
• 16 Ссылки
• 17 Внешние ссылки

Термин сила (латинское : потенция, potestas, dignitas) - это неправильный перевод древнегреческого δύναμις (dúnamis, здесь: «усиление»), использованного греческим математиком Евклидом для обозначения квадрата, следующая за Гиппократом Хиос. Архимед открыл и доказал закон экспонент, 10 ⋅ 10 = 10, необходимое для манипулирования степен 10. В 9 веке персидский математик Мухаммад ибн Муса аль-Хваризми использовал термины مَال (мал, «имущество »,« Собственность ») для квадрата - мусульмане,« как и большинство математиков того и более раннего времени, считали числа в квадрате как изображения площади, особенно земли, следовательно, собственность »- и كَعْبَة (kaʿbah, "куб") для куба, который позже математики в математической записи буквами mīm (m) и kāf (k), соответственно, к 15 веку, как видно из работы Абу аль-Хасана ибн Али аль-Каласади.

В конец 16 века Йост Бюрджи использовал римские цифры

Николя Шуке использовал форму экспоненциальной записи в 15 веке, которая позже была использована Хенрикусом Грамматеусом и Майкл Стифель в 16 веке. было придумано в 1544 году Майклом Стифелем. Сэмюэл Джик ввел термин индексы в 1696 году. В 16-м веке Роберт Рекорд использовал термины квадрат, куб, зензицензик (четвертая степень ), сурсолид (пятая), зензикубе (шестая), вторая сурсолидная (седьмая) и зензизензизензическая (восьмая). Биквадрат также использовался для обозначения четвертой степени.

В начале 17 века первая форма нашей экспоненциальной записи была введена Рене Декартом в его тексте под названием La Géométrie ; Здесь обозначение вводится в Книге I.

Некоторые математики (например, Исаак Ньютон ) использовали экспоненты только для степеней больше двух, предпочтая квадраты как повторяющееся умножение. Таким образом они могли бы записать полиномы , например, как ax + bxx + cx + d.

Другой исторический синоним, инволюция, сейчас встречается редко, и его не следует путать с его более распространенным значением.

В 1748 году Леонард Эйлер писал :

«рассматривайте показатели или степени, в которых показатель степени является показателем. Ясно, что такого рода не являются алгебраическими функциями, поскольку в них показатели должны быть постоянными ».

С Введение трансцендентных функций, Эйлер заложил основу для современного введения натурального логарифма - как обратной функции для натуральной экспоненциальной функции, f (x) = е.

Выражение b = b ⋅ b называется «квадрат b» или «b в квадрате», потому что площадь квадрата с длиной стороны б есть б.

Точно так же выражение b = b ⋅ b ⋅ b называется «куб из b» или «b в кубе», потому что объем куба с стороны длиной b равен b.

Когда это положительное целое число, показатель степени указывает, сколько копий основания умножаются вместе. Например, 3 = 3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 = 243. База 3 появляется 5 раз при повторном умножении, потому что показатель степени равен 5. Здесь 243 - это 5-я степень 3 или 3 в 5-й степени. сила.

Слово «приподнятый» обычно опускается, а иногда и «мощность», поэтому 3 можно просто читать «от 3 до 5» или «от 3 до 5». Следовательно, возведение в степень b можно выразить как «b в степень n», «b в степень n», «b в степень n» или, наиболее кратко, как «b в степень n».

Операция возведения в степени с целыми показателями может быть определена непосредственно из элементарных арифметических операций.

Положительные показатели

Могут быть оцененными степенью с положительными целыми Показателем по базовому случаю

$b\; 1\; =\; b\; \{\backslash \; displaystyle\; b\; ^\; \{1\}\; =\; b\}$

и рекуррентным представлением

$млрд\; +\; 1\; =\; млрд\; b.\; \{\backslash \; displaystyle\; b\; ^\; \{n\; +\; 1\}\; =\; b\; ^\; \{n\}\; \backslash \; cdot\; b.\}$

ассоциативность умножения означает, что для любых положительных целых чисел m и n

$bm\; +\; n\; =\; bm\; \cdot \; bn.\; \{\backslash \; displaystyle\; b\; ^\; \{m\; +\; n\}\; =\; b\; ^\; \{m\}\; \backslash \; cdot\; b\; ^\; \{n\}.\}$

Нулевой показатель

Любое ненулевое число, возведенное в степень 0, равно 1:

$b\; 0\; =\; 1.\; \{\backslash \; displaystyle\; b\; ^\; \{0\}\; =\; 1.\}$

Одна интерпретация такой степени - это пустой продукт.

Случай 0 более сложен, и выбор того, присвоение ему значения, и какое значение присвоить может зависеть от контекста. Дополнительные сведения см. В разделе От нуля до степени нуля.

Отрицательные показатели

Для любого целого числа n и ненулевого b выполняется следующее тождество:

$b\; -\; n\; =\; 1\; b\; n.\; \{\backslash \; displaystyle\; b\; ^\; \{-\; n\}\; =\; \{\backslash \; frac\; \{1\}\; \{b\; ^\; \{n\}\}\}.\}$

Возведение 0 в отрицательную степень не определено, но в некоторых случаях это может интерпретироваться как бесконечность (∞).

Приведенная выше личность может быть получена посредством определения, направленного на расширение диапазона показателей до отрицательных целых чисел.

Для ненулевого b и положительного n рекуррентное соотношение, приведенное выше, можно переписать как

$bn\; =\; bn\; +\; 1\; b,\; n\; \ge \; 1.\; \{\backslash \; displaystyle\; b\; ^\; \{n\}\; =\; \{\backslash \; frac\; \{b\; ^\; \{n\; +\; 1\}\}\; \{b\}\},\; \backslash \; quad\; n\; \backslash \; geq\; 1.\}$

Из определения этих отношений как действительного для всех целых n и ненулевых b, следует, что

$b\; 0\; =\; b\; 1\; b\; =\; 1,\; b\; -\; 1\; =\; b\; 0\; b\; =\; 1\; b,\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; b\; ^\; \{0\}\; =\; \{\backslash \; frac\; \{b\; ^\; \{1\}\}\; \{b\}\}\; =\; 1,\; \backslash \backslash \; [3pt]\; b\; ^\; \{-\; 1\}\; =\; \{\backslash \; frac\; \{b\; ^\; \{0\}\}\; \{b\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{b\}\},\; \backslash \; end\; \{align\}\}\}$

и более в целом для любого ненулевой b и любое неотрицательное целое n,

$b\; -\; n\; =\; 1\; млрд.\; \{\backslash \; displaystyle\; b\; ^\; \{-\; n\}\; =\; \{\backslash \; frac\; \{1\}\; \{b\; ^\; \{n\}\}\}.\}$

Тогда легко показать, что это верно для любого целого числа n.

Тождества и свойства

Следующие идентичности верны для всех целочисленных показателей при условии, что основание не равно нулю:

$bm\; +\; n\; =\; bm\; \cdot \; bn\; (bm)\; n\; знак\; равно\; bm\; \cdot \; N\; (b\; \cdot \; c)\; n\; =\; bn\; \cdot \; cn\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; b\; ^\; \{m\; +\; n\}\; =\; b\; ^\; \{m\}\; \backslash \; cdot\; b\; ^\; \{n\}\; \backslash \backslash \backslash \; left\; (b\; ^\; \{m\}\; \backslash \; right)\; ^\; \{n\}\; =\; b\; ^\; \{m\; \backslash \; cdot\; n\}\; \backslash \backslash \; (b\; \backslash \; cdot\; c)\; ^\; \{n\}\; =\; b\; ^\; \{n\}\; \backslash \; cdot\; c\; ^\; \{n\}\; \backslash \; end\; \{align\}\}\}$

Отличие от сложения и умножения:

• Возведение в степень не коммутативное. Например, 2 = 8 ≠ 3 = 9.
• Возведение в степень не является ассоциативным. Например, (2) = 8 = 4096, тогда как 2 = 2 = 2417851639229258349412352. Без скобок обычный порядок операций для последовательного возведения в степень в надстрочной нотации - сверху вниз (или правоассоциативный), а не восходящий (или левоассоциативный). То есть

  $bpq\; =\; b\; (pq),\; \{\backslash \; displaystyle\; b\; ^\; \{p\; ^\; \{q\}\}\; =\; b\; ^\; \{\backslash \; left\; (p\; ^\; \{q\}\; \backslash \; right)\},\}$

  что, как правило,, отличается от

  $(bp)\; q\; =\; bpq.\; \{\backslash \; displaystyle\; \backslash \; left\; (b\; ^\; \{p\}\; \backslash \; right)\; ^\; \{q\}\; =\; b\; ^\; \{pq\}.\}$

Степени суммы

Степени суммы обычно можно вычислить из степени слагаемых по биноми формуле

$(a\; +\; b)\; n\; =\; \sum \; я\; знак\; равно\; 0\; n\; (ni)\; aibn\; -\; я\; =\; \sum \; i\; =\; 0\; nn!\; я!\; (п\; -\; я)!\; а\; я\; б\; н\; -\; я.\; \{\backslash \; displaystyle\; (a\; +\; b)\; ^\; \{n\}\; =\; \backslash \; sum\; \_\; \{i\; =\; 0\}\; ^\; \{n\}\; \{\backslash \; binom\; \{n\}\; \{i\}\}\; a\; ^\; \{i\}\; b\; ^\; \{ni\}\; =\; \backslash \; sum\; \_\; \{\; я\; =\; 0\}\; ^\; \{n\}\; \{\backslash \; frac\; \{n!\}\; \{я!\; (ni)!\}\}\; a\; ^\; \{i\}\; b\; ^\; \{ni\}.\}$

Однако этала верна, только если слагаемые коммутируют (т.е. ab = ba), что подразумевается, если они принадлежат структуре , которая является коммутативной. В противном случае, если a и b являются, скажем, квадратными матрицами одинакового размера, эту формулу использовать нельзя. Отсюда следует, что в компьютерной алгебре многие алгоритмы, включающие целочисленные показатели, должны быть, когда базы возведения в степень не коммутируются. Некоторые универсальные системы компьютерной алгебры используют другую нотацию (иногда ^^ вместо ^) для возведения в степень с некоммутирующими базами, которое называется некоммутативным возведением в степени .

комбинаторная интерпретация

Длярицательных целых чисел n и неотъемлемое значение n - это функции из набора из m элементов до набора из n элементов (см. кардинальное возведение в степень ). Такие функции могут быть представлены как m- кортежи из n-элементного набора (или как m-буквенные слова из n-буквенного алфавита). Некоторые примеры значений m и n, представленных в следующей таблице:

n	n найден наборов m элементов из набора {1,..., n}
$0\; 5\; =\; 0\; \{\backslash \; displaystyle\; 0\; ^\; \{5\}\; =\; 0\}$	нет
$1\; 4\; =\; 1\; \{\backslash \; displaystyle\; 1\; ^\; \{4\}\; =\; 1\}$	$(1,\; 1,\; 1,\; 1)\; \{\backslash \; displaystyle\; (1,1,1,\; 1)\}$
$2\; 3\; =\; 8\; \{\backslash \; displaystyle\; 2\; ^\; \{3\}\; =\; 8\}$	$(1,\; 1,\; 1),\; (1,\; 1,\; 2),\; (1,\; 2,\; 1),\; (1,\; 2,\; 2),\; (\; 2,\; 1,\; 1),\; (2,\; 1,\; 2),\; (2,\; 2,\; 1),\; (2,\; 2,\; 2)\; \{\backslash \; displaystyle\; (1,1,1),\; (1,1,2),\; (\; 1,2,1),\; (1,2,2),\; (2,1,1),\; (2,1,2),\; (2,2,1),\; (2,\; 2,2)\}$
$3\; 2\; =\; 9\; \{\backslash \; displaystyle\; 3\; ^\; \{2\}\; =\; 9\}$	$(1,\; 1),\; (1,\; 2),\; (1,\; 3),\; (2,\; 1),\; (2,\; 2),\; (2,\; 3),\; (3,\; 1),\; (3,\; 2),\; (3,\; 3)\; \{\backslash \; Displaystyle\; (1,1),\; (1,2),\; (1,3),\; (2,1),\; (2,\; 2),\; (2,3),\; (3,1),\; (3,2),\; (3,3)\}$
$4\; 1\; =\; 4\; \{\backslash \; Displaystyle\; 4\; ^\; \{1\}\; =\; 4\}$	$(\; 1),\; (2),\; (3),\; (4)\; \{\backslash \; displaystyle\; (1),\; (2),\; (3),\; (4)\}$
$5\; 0\; =\; 1\; \{\backslash \; displaystyle\; 5\; ^\; \{0\}\; =\; 1\; \}$	$()\; \{\backslash \; displaystyle\; ()\}$

Конкретные основания

Степени десятичного

В десятичном (деци mal ), целые степени 10 записываются к ак цифра 1, за которую или перед ней стоит количество нулей, определяемое знаком и величиной экспоненты. Например, 10 = 1000 и 10 = 0,0001.

Возведение в степень с основанием 10 используется в экспоненциальном представлении для обозначения больших или малых чисел. Например, 299792458 м / с (света в вакууме, в метров в секунду ) можно записать как 2,99792458 × 10 м / с, а приблизительно как 2,998 × 10 м / с.

Префиксы SI, основанные на степени 10, используются также для описания малых или больших количеств. Например, префикс килограмм означает 10 = 1000, поэтому километр равен 1000 м.

Степень двойки

Первые отрицательные степени двойки обычно используются и имеют специальные названия, половина и четверть.

Степень двойки появляются в теории множеств, поскольку набор с мощностью элементов имеет набор, набор всех его подмножеств, который имеет 2 элемента.

Целочисленные степени двойки важны в информатике. Положительные целые степени 2 дают количество значений для n- бит целое число двоичное число ; например, байт может принимать 2 = 256 различных значений. В двоичной системе счисления любое число выражается как сумма степеней двойки и обозначается как последовательность из 0 и 1, разделенных двоичной системой счисления , где 1 указывает степень 2, что фигурирует в сумме; показатель степени определяющей единицы: неотрицательные показатели - это ранг 1 слева от точки (начиная с 0), а отрицательные значения рангом от точки.

Степени единицы

Степени единицы равны единице: 1 = 1.

Степени нуля

Если показатель степени n положителен (n>0), n- я степень нуля равна нулю: 0 = 0.

Если показатель степени n отрицательный (n < 0), the nth power of zero 0 is undefined, because it must equal $1/0\; -\; n\; \{\backslash \; displaystyle\; 1/0\; ^\; \{-\; n\}\}$с -n>0, и это будет $1/0\; \{\backslash \; displaystyle\; 1/0\}$в соответствии с вышеизложенным.

Выражение 0 либо равно как 1 или остается неопределенным (см. Ноль в степени нуля ).

Степени отрицательной единицы

Если n - четное целое число, то (−1) = 1.

Если n - нечетное целое число, то (−1) = −1.

Из-за этой степени −1 полезны для выражения чередования следовать. Аналогичное обсуждение степеней комплексного числа i см. в разделе § Степени комплексных чисел.

Большие показатели

превышают степеней числа больше единицы расходится, иными словами, последовательность неограни ченно растет:

b → ∞ при n → ∞ wh en b>1

Это можно прочитать как «b в степени n стремится к + ∞, поскольку n стремится к бесконечности, когда b больше единицы ».

Степени числа с абсолютным значением меньше единицы стремятся к нулю:

b → 0 при n → ∞, когда | б | < 1

Любая степень единицы всегда равна единице:

b = 1 для всех n, если b = 1

Степени –1 чередуются между 1 и –1, поскольку n чередуется между четным и нечетным, и, следовательно, не стремится до любого предела по мере роста.

Если возведенное в степени число изменяется, стремясь к 1, так как показатель степени стремится к бесконечности, то предел не обязательно является одним из указанных выше. Особенно важным случаем является

(1 + 1 / n) → e при n → ∞

См. § Показательная функция ниже.

Другие ограничения, в частности те, которые имеют выражения неопределенной, развития в § Пределы полномочий ниже.

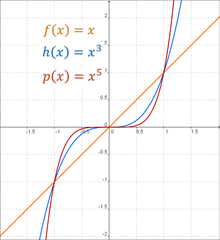Степенные функции

Степенные функции для $n\; =\; 1,\; 3,\; 5\; \{\backslash \; displaystyle\; n\; =\; 1,3,5\}$ Степенные функции для $n\; =\; 2,\; 4,\; 6\; \{\backslash \; displaystyle\; n\; =\; 2,4,6\}$

Действительные функции вида $f\; (x)\; =\; cxn\; \{\backslash \; displaystyle\; f\; (x)\; =\; cx\; ^\; \{n\}\}$, где $c\; \ne \; 0\; \{\backslash \; displaystyle\; c\; \backslash \; neq\; 0\}$, иногда называются степенными функциями. Когда $n\; \{\backslash \; displaystyle\; n\}$является целым числом и $n\; \ge \; 1\; \{\backslash \; displaystyle\; n\; \backslash \; geq\; 1\}$, два основных семейства существуют: для $n\; \{\backslash \; displaystyle\; n\}$четный и для $n\; \{\backslash \; displaystyle\; n\}$нечетный. Обычно для $c>0\; \{\backslash \; displaystyle\; c>0\}$, когда $n\; \{\backslash \; displaystyle\; n\}$четно $f\; (x)\; =\; cxn\; \{\backslash \; displaystyle\; f\; (x)\; =\; cx\; ^\; \{n\}\}$будет стремиться к положительной бесконечности при увеличении $x\; \{\backslash \; displaystyle\; x\}$, а также к положительной бесконечности при уменьшении $x\; \{\backslash \; displaystyle\; x\}$. Все графики из семейства четных степенных функций имеют общую форму $y\; =\; cx\; 2\; \{\backslash \; displaystyle\; y\; =\; cx\; ^\; \{2\}\}$, сглаживаясь больше в средняя по мере увеличения $n\; \{\backslash \; displaystyle\; n\}$. Функции с такой симметрией ($f\; (-\; x)\; =\; f\; (x)\; \{\backslash \; displaystyle\; f\; (-\; x)\; =\; f\; (x)\}$) вызываются четными функциями.

, когда $n\; \{\backslash \; displaystyle\; n\}$равно нечетное, $f\; (x)\; \{\backslash \; displaystyle\; f\; (x)\}$s асимпт отическое поведение меняется с положительного $x\; \{\backslash \; displaystyle\; x\}$на отрицательное $x\; \{\backslash \; displaystyle\; x\}$. Для $c>0\; \{\backslash \; displaystyle\; c>0\}$, $f\; (x)\; =\; cxn\; \{\backslash \; displaystyle\; f\; (x)\; =\; cx\; ^\; \{n\}\}$также будет иметь тенденцию к положительному бесконечность с повреждением $x\; \{\backslash \; displaystyle\; x\}$, но в сторону отрицательной бесконечности с уменьшением $x\; \{\backslash \; displaystyle\; x\}$. нечетные степенные функции имеют общую форму $y\; =\; cx\; 3\; \{\backslash \; displaystyle\; y\; =\; cx\; ^\; \{3\}\}$, сглаживаясь посередине как $n\; \{\backslash \; displaystyle\; n\}$увеличить и теряет всю плоскостность на прямой для $n\; =\; 1\; \{\backslash \; displaystyle\; n\; =\; 1\}$. Функции с таким симметрией ($f\; (-\; x)\; =\; -\; f\; (x)\; \{\backslash \; displaystyle\; f\; (-x)\; =\; -\; f\; (x)\}$) называются нечетными функциями.

Для противоположное асимптотическое поведение верно в каждом случае.

Спи сок степеней целых чисел

n	n	n	n	n	n	n	n	n	n
2	4	8	16	32	64	128	256	512	1024
3	9	27	81	243	729	2187	6561	19683	59049
4	16	64	256	1024	4096	16384	65536	262144	1048576
5	25	125	625	3125	15625	78125	390625	1953125	9765625
6	36	216	1296	7776	46656	279936	1679616	10077696	60466176
7	49	343	2401	16807	117649	823543	5764801	40353607	282475249
8	64	512	4096	32768	262144	2097152	16777216	134217728	1073741824
9	81	729	6561	59049	531441	4782969	43046721	387420489	3486784401
10	100	1000	10000	100000	1000000	10000000	100000000	1000000000	10000000000

Сверху вниз: x, x, x, x, x, x, x.

n-й корень из числа b - это число x такое что x = b.

Если b - положительное действительное число, а n - положительное целое число, то существует ровно одно положительное действительное решение x = b. Это решение называется основным корнем н-й степени из б. Он обозначается как √b, где √ - это символ радикала ; в качестве альтернативы основного корень можно записать как б. Например: 9 = √9 = 3 и 8 = √8 = 2.

Тот факт, что $x\; =\; b\; 1\; n\; \{\backslash \; displaystyle\; x\; =\; b\; ^\; \{\backslash \; frac\; \{1\}\; \{n\}\; \}\}$решает $xn\; =\; b\; \{\backslash \; displaystyle\; x\; ^\; \{n\}\; =\; b\}$следует из, что

$xn\; =\; (b\; 1\; n)\; n\; =\; b\; 1\; n\; \times \; b\; 1\; n\; \times \; \cdots \; \times \; b\; 1\; n\; ⏟\; n\; раз\; =\; b\; (1\; n\; +\; 1\; n\; +\; \cdots \; +\; 1\; n)\; ⏟\; n\; раз\; =\; bnn\; =\; b\; 1\; =\; b.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; x\; ^\; \{n\}\; =\; \backslash \; left\; (b\; ^\; \{\backslash \; frac\; \{1\}\; \{n\}\}\; \backslash \; right)\; ^\; \{n\}\; =\; \backslash \; underbrace\; \{b\; ^\; \{\backslash \; frac\; \{1\}\; \{n\}\}\; \backslash \; times\; b\; ^\; \{\backslash \; frac\; \{1\}\; \{n\}\}\; \backslash \; times\; \backslash \; cdots\; \backslash \; times\; b\; ^\; \{\backslash \; frac\; \{1\}\; \{n\}\}\}\; \_\; \{n\; \backslash ,\; \{\backslash \; textrm\; \{times\}\}\}\; \backslash \backslash \; =\; b\; ^\; \{\backslash \; underbrace\; \{\backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{n\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{n\}\}\; +\; \backslash \; cdots\; +\; \{\backslash \; frac\; \{1\}\; \{n\}\}\; \backslash \; right)\}\; \_\; \{n\; \backslash ,\; \{\backslash \; textrm\; \{times\}\}\}\}\; =\; b\; ^\; \{\backslash \; frac\; \{n\}\; \{n\}\}\; =\; b\; ^\; \{1\}\; =\; b.\; \backslash \; end\; \{align\}\}\}$

Если b равно 0, уравнение x = b имеет одно решение: x = 0.

Если n равно , даже и b положительно, то x = b имеет два действительных решения, которые являются положительными и отрицательными корнями n-й степени из b, то есть b>0 и - (b) < 0.

Если n четно, а b отрицательно, уравнение не имеет решения в действительных числах.

Если n нечетно, то x = b имеет ровно одно действительное решение, которое положительно, если b положительно (b>0), и отрицательно, если b отрицательно (b < 0).

Принимая положительное вещественное число b до рациональной экспоненты u / v, где u - целое число, а v - положительное целое число, и учитывая только главные корни, дает

$buv\; =\; (bu)\; 1\; v\; =\; buv\; =\; (b\; 1\; v)\; u\; =\; (bv)\; u.\; \{\backslash \; displaystyle\; b\; ^\; \{\backslash \; frac\; \{u\}\; \{v\}\}\; =\; \backslash \; left\; (b\; ^\; \{u\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{1\}\; \{v\}\}\; =\; \{\backslash \; sqrt\; [\{\; v\}]\; \{b\; ^\; \{u\}\}\}\; =\; \backslash \; left\; (b\; ^\; \{\backslash \; frac\; \{1\}\; \{v\}\}\; \backslash \; right)\; ^\; \{u\}\; =\; \backslash \; left\; (\{\backslash \; sqrt\; [\{v\}]\; \{b\}\}\; \backslash \; right)\; ^\; \{u\}.\}$

Преобразование отрицательного действительного числа b в рациональную степень u / v, где u / v выражается в младших членах, дает положительный реальный результат, если u четно, и, следовательно, v нечетно, потому что тогда b положительно; и дает отрицательный действительный результат, если u и v оба нечетны, потому что тогда b отрицательно. Случай четного v (и, следовательно, нечетного u) н е может рассматриваться таким образом в действующем вещественном числе, поскольку x = −1, значение b в этом случае использовать мнимую единицу i, как более подробно описано в разделе § Степени комплексных чисел.

Таким образом, мы имеем (−27) = −3 и (−27) = 9. Число 4 имеет две степени 3/2, а именно 8 и −8; однако по соглашению в обозначении 4 используется главный корень и получается 8. Использование корня v-й степени степени u / v также называется корнем v / u-й степени, а для даже v термин главный корень означает также положительный результат.

Этунозначность знака необходимо учитывать при использовании приспособлений мощности. Например:

$-\; 27\; =\; (-\; 27)\; ((2\; 3)\; (3\; 2))\; =\; ((-\; 27)\; 2\; 3)\; 3\; 2\; =\; 9\; 3\; 2\; =\; 27\; \{\backslash \; displaystyle\; -27\; =\; (-\; 27)\; ^\; \{\backslash \; left\; (\backslash \; left\; (\{\backslash \; frac\; \{2\}\; \{3\}\}\; \backslash \; right)\; \backslash \; left\; (\{\backslash \; frac\; \{3\}\; \{2\}\}\; \backslash \; right)\; \backslash \; right)\}\; =\; \backslash \; left\; ((-\; 27)\; ^\; \{\; \backslash \; frac\; \{2\}\; \{3\}\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{3\}\; \{2\}\}\; =\; 9\; ^\; \{\backslash \; frac\; \{3\}\; \{2\}\}\; =\; 27\}$

явно неверно. Проблема начинается уже в первом равенстве, когда вводятся стандартные обозначения для изначально неоднозначной ситуации - требуется четный корень - и просто неверно полагается на одну, традиционную или основную интерпретацию. Та же проблема возникает и с неправильно введенной заменой нотации, которая по своей сути обеспечивает положительный результат:

$((-\; 27)\; 2\; 3)\; 3\; 2\; =\; ((-\; 27)\; 2\; 3)\; 3\; =\; (-\; 27)\; 2\; \ne \; -\; 27\; \{\backslash \; displaystyle\; \backslash \; left\; ((-\; 27)\; ^\; \{\backslash \; frac\; \{2\}\; \{3\}\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{3\}\; \{2\}\}\; =\; \{\backslash \; sqrt\; \{\backslash \; left\; (\{\backslash \; sqrt\; [\{3\; \}]\; \{(-\; 27)\; ^\; \{2\}\}\}\; \backslash \; right)\; ^\; \{3\}\}\}\; =\; \{\backslash \; sqrt\; \{(-27)\; ^\; \{2\}\}\}\; \backslash \; neq\; -27\}$

вместо

$(\; (-\; 27)\; 2\; 3)\; 3\; 2\; =\; -\; ((-\; 27)\; 2\; 3)\; 3\; =\; -\; (-\; 27)\; 2\; =\; -\; 27.\; \{\backslash \; displaystyle\; \backslash \; left\; ((-\; 27)\; ^\; \{\backslash \; frac\; \{2\}\; \{3\; \}\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{3\}\; \{2\}\}\; =\; -\; \{\backslash \; sqrt\; \{\backslash \; left\; (\{\backslash \; sqrt\; [\{3\}]\; \{(-\; 27)\; ^\; \{2\}\}\}\; \backslash \; right)\; ^\; \{3\; \}\}\}\; =\; -\; \{\backslash \; sqrt\; \{(-27)\; ^\; \{2\}\}\}\; =\; -\; 27.\}$

Как правило, для комплексных чисел возникают проблемы того же типа, что развития в разделе § Отказ тождества степени и логарифма.

Возведение в степень до действительных степеней положительных действительных чисел может быть определено путем увеличения рациональных степеней до действительных чисел по непрерывности, либ о, как правило, указано в § Полномочия через логарифмы ниже. Результатом всегда является положительное действительное число, и тождества и свойства, показанные выше для целочисленных показателей, также верны для положительных вещественных оснований с нецелочисленными показателями.

С другой стороны, возведение в степень до действительной степени отрицательного числа действительного числа труднее определить несколько значений, поскольку оно может быть нереальным и иметь несколько значений (см. § Действительные показатели с отрицательными базами). Можно выбрать одно из этих значений, называемое основным значением, но нет выбора основного значения, для которого такой идентификатор, как

$(br)\; s\; =\; br\; \cdot \; s\; \{\backslash \; displaystyle\; \backslash \; left\; (b\; ^\; \{r\; \}\; \backslash \; right)\; ^\; \{s\}\; =\; b\; ^\; \{r\; \backslash \; cdot\; s\}\}$

верно; см. § Отказ от тождества мощности и логарифма. Следовательно, возведение в степень с базисом, являющимся положительным лицом, обычно рассматриваемым как многозначная функция.

Пределы рациональных показателей

Временная экспоненциальная функция непрерывна, мы находим $lim\; n\; \to \; \infty \; exn\; =\; е\; lim\; n\; \to \; \infty \; Иксn\; \{\backslash \; Displaystyle\; \backslash \; lim\; \_\; \{п\; \backslash \; к\; \backslash \; infty\}\; e\; ^\; \{x\_\; \{n\}\}\; =\; e\; ^\; \{\backslash \; lim\; \_\; \{n\; \backslash \; to\; \backslash \; infty\}\; x\_\; \{n\}\}\}$для сходящихся последовательностей (x n). Это показано здесь для x n = 1 / n.

Гидравлическое любое иррациональное число может быть выражено как предел показывает показ эффективных чисел, возведение в степень положительного действительного числа b с произвольным вещественным средством x можно определить по непрерывности с правилом

$bx\; =\; lim\; r\; (\in \; Q)\; \to \; xbr\; (b\; \in \; R\; +,\; x\; \in \; R),\; \{\backslash \; displaystyle\; b\; ^\; \{x\}\; =\; \backslash \; lim\; \_\; \{r\; (\backslash \; in\; \backslash \; mathbb\; \{Q\})\; \backslash \; to\; x\}\; b\; ^\; \{r\}\; \backslash \; quad\; (b\; \backslash \; in\; \backslash \; mathbb\; \{R\}\; ^\; \{+\},\; \backslash ,\; x\; \backslash \; in\; \backslash \; mathbb\; \{R\}),\}$

где предел, когда r приближается к x, берется только по рациональным значениям r. Этот предел существует только для положительного b. Используется (ε, δ) -определение предела ; это включает в себя демонстрацию того, что для любой желаемой точности результата b можно выбрать достаточно малый интервал вокруг x, чтобы все рациональные степени в интервале находились в пределах желаемой точности.

, если x = π, можно использовать неокрывающееся десятичное представление π = 3,14159… (на основе строгой монотонности рациональной степени) для достижения интервалов, ограниченных рациональных степенями

$[b\; 3,\; б\; 4]\; \{\; \backslash \; displaystyle\; \backslash \; left\; [b\; ^\; \{3\},\; b\; ^\; \{4\}\; \backslash \; right]\}$, $[b\; 3.1,\; b\; 3.2]\; \{\backslash \; displaystyle\; \backslash \; left\; [b\; ^\; \{3.1\},\; b\; ^\; \{3.2\}\; \backslash \; right]\; \}$, $[b\; 3.14,\; b\; 3.15]\; \{\backslash \; displaystyle\; \backslash \; left\; [b\; ^\; \{3.14\},\; b\; ^\; \{3.15\}\; \backslash \; right]\}$, $[b\; 3.141,\; b\; 3.142]\; \{\backslash \; displaystyle\; \backslash \; left\; [b\; ^\; \{3.141\},\; b\; ^\; \{3.142\}\; \backslash \; right]\}$, $[b\; 3.1415,\; b\; 3.1416]\; \{\backslash \; displaystyle\; \backslash \; left\; [b\; ^\; \{3.1415\},\; b\; ^\; \{3.1416\}\; \backslash \; right]\}$, $[b\; 3.14159,\; b\; 3.14160]\; \{\backslash \; displaystyle\; \backslash \; left\; [b\; ^\; \{3.14159\},\; b\; ^\; \{3.14160\}\; \backslash \; right]\}$, $\dots \; \{\backslash \; displaystyle\; \backslash \; ldots\}$

Ограниченные интервалы сходятся к единственному вещественному числу, обозначаемое $б\; \pi \; \{\backslash \; displaystyle\; b\; ^\; \{\backslash \; pi\}\}$. Этот метод можно использовать для получения степени положительного действительного числа b для любого иррационального показателя степени. Таким образом, функция f b (x) = b определена для любого действительного числа x.

Экспоненциальная функция

Важная математическая константа e, иногда называемая числом Эйлера, примерно равно 2,718 и является основанием натуральный логарифм. Хотя возведение в степень е можно, в принципе, рассматривать так же, как возведение в степень любого другого действующего числа, такие экспоненты обладают особенно элегантными и полезными свойствами. Среди прочего эти позволяют естественным образом обобщать экспоненты от электронных показателей, такие как комплексные числа или даже матрицы, совпадающие со сроками совместимых показателей.

Как следствие, обозначение обычно обозначает обобщенное определение возведения в степени, называемое экспоненциальной функцией, exp (x), которая может быть определена различными эквивалентными способами, например, по

$ехр\; \; (x)\; =\; lim\; n\; \to \; \infty \; (1\; +\; xn)\; n.\; \{\backslash \; displaystyle\; \backslash \; exp\; (x)\; =\; \backslash \; lim\; \_\; \{n\; \backslash \; to\; \backslash \; infty\}\; \backslash \; left\; (1\; +\; \{\backslash \; frac\; \{x\}\; \{n\}\}\; \backslash \; right)\; ^\; \{n\}.\}$

Среди других свойств exp удовлетворяет экспоненциальному тождеству

$exp\; \; (x\; +\; y)\; =\; exp\; \; (x)\; \cdot \; exp\; \; (y).\; \{\backslash \; displaystyle\; \backslash \; exp\; (x\; +\; y)\; =\; \backslash \; exp\; (x)\; \backslash \; cdot\; \backslash \; exp\; (y).\}$

Экспоненциальная функция определена для всех целых, дробных, вещественных и комплексных значений из х. Фактически, экспоненциальная матрица хорошо определена для квадратных матриц (в этом случае это экспоненциальное тождество выполняется только тогда, когда x и y коммутируют) и полезны для решения систем линейные дифференциальные уравнения.

exp (1) равно e, а exp (x) удовлетворяет экспоненциальному тождеству, немедленно, что exp (x) совпадает с определением повторного умножения e для целого числа x, а также следовательно, рациональные степени обозначают (положительные) корни, как обычно, поэтому exp (x) совпадает с определениями e из предыдущего раздела для всех действующих x по непрерывности.

Вычисляет степень с помощью логарифмов

Когда e определяется как экспоненциальная функция, b может быть определено для других положительных действительных чисел b через e. В частности, натуральный логарифм ln (x) является обратной величиной экспоненциальной функцией e. Он определен для b>0 и удовлетворяет

$b\; =\; e\; ln\; \; b.\; \{\backslash \; displaystyle\; b\; =\; e\; ^\; \{\backslash \; ln\; b\}.\}$

Если b должен сохранить правила логарифма и экспоненты, то должно быть

$bx\; =\; (e\; ln\; \; b)\; x\; =\; ex\; \cdot \; ln\; \; b\; \{\backslash \; displaystyle\; b\; ^\; \{x\}\; =\; \backslash \; left\; (e\; ^\; \{\backslash \; ln\; b\}\; \backslash \; right)\; ^\; \{x\}\; =\; e\; ^\; \{x\; \backslash \; cdot\; \backslash \; ln\; b\}\}$

для каждого действительного числа x.

Это может быть альтернативное определение степени b действительного числа и согласуется с определением, данным выше с использованием рациональных показателей степени и непрерывности. Определение возведения в степень с использованием логарифмов чаще встречается в контексте комплексных чисел, как обсуждается ниже.

Действующие показатели с отрицательным основанием

Степени положительного действительного числа всегда являются положительными действительными числами. Однако решение x = 4 может быть либо 2, либо −2. Главное значение 4 - 2, но −2 также является правильным квадратным корнем. Если определение возведения в степень действительных чисел будет расширено, чтобы разрешить отрицательные результаты, то результат будет больше не будет корректным.

Ни метод логарифмирования, ни методы рациональной экспоненты нельзя использовать для определения b как действительного числа для отрицательного действительного числа b и произвольного действительного числа r. Действительно, e положительно для любого действительного числа r, поэтому ln (b) не определяется как действительное число для b ≤ 0.

Метод рациональной экспоненты не может использоваться для отрицательных значений b, потому что он полагается на непрерывность. Функция f (r) = b имеет уникальное непрерывное продолжение от рациональных чисел до действительных чисел для каждого b>0. Но когда b < 0, the function f is not even continuous on the set of rational numbers r for which it is defined.

Например, рассмотрим b = −1. Корень n-й степени из −1 равен −1 для любого нечетного натурального числа n. Таким образом, если n - нечетное положительное целое число, (−1) = −1, если m нечетно, и (−1) = 1, если m четно. Таким образом, множество рациональных чисел q, для которых (−1) = 1, плотно в рациональных числах, как и множество q, для которых (−1) = −1. Это означает, что функция (−1) не является непрерывной ни при каком рациональном числе q, где она определена.

С другой стороны, произвольные комплексные степени отрицательных чисел b могут быть определены путем выбора комплексного логарифма числа b.

Иррациональные показатели

Если b - положительное вещественное алгебраическое число, а x - рациональное число, выше было показано, что b - алгебраическое число. Это остается верным, даже если принять любое алгебраическое число в качестве b, с той лишь разницей, что b может принимать несколько значений (конечное число, см. Ниже), которые все являются алгебраическими. Теорема Гельфонда – Шнайдера дает некоторую информацию о природе b, когда x иррационально (то есть не рационально). В нем говорится:

Если b - алгебраическое число, отличное от 0 и 1, а x - иррациональное алгебраическое число, то все значения b (их бесконечно много) являются трансцендентными (то есть не алгебраическими

Если b - положительное действительное число, а z - любое комплексное число, степень b определяется как

$bz\; =\; (е\; пер\; \; б)\; Z\; знак\; равно\; е\; (z\; пер\; \; б),\; \{\backslash \; Displaystyle\; Ь\; ^\; \{z\}\; =\; \backslash \; влево\; (е\; ^\; \{\backslash \; ln\; б\}\; \backslash \; вправо)\; ^\; \{г\}\; =\; е\; ^\; \{(г\; \backslash \; пер\; b)\},\}$

где x = ln (b) - единственное действительное решение уравнения e = b, а комплексная степень e определяется экспоненциальной функцией , которая является единственной функция комплексной переменной, которая равна своей производной и принимает значение 1 для x = 0.

Поскольку, как правило, b не является реальным набором с дополнительной структурой . Например, в линейной алгебре имеет индексировать прямые суммы векторных пространств по произвольным индексным наборам. То есть, мы можем говорить о

$⨁\; i\; \in \; NV\; i,\; \{\backslash \; displaystyle\; \backslash \; bigoplus\; \_\; \{i\; \backslash \; in\; \backslash \; mathbb\; \{N\}\}\; V\_\; \{i\},\}$

, где каждое V i - пространство.

Тогда, если V i = V для каждого i, результирующая прямая сумма может быть записана в экспоненциальной записи как V или просто V с пониманием, что прямая сумма является размером по умолчанию. Мы снова можем заменить набор N на число n, чтобы получить V, хотя без выбора конкретного стандартного набора с числом элементов n он определяется только от до изоморфизм. Принимая V за поле Rиз вещественных чисел (рассматриваемое как векторное пространство над собой) и за n как некоторое натуральное число, мы получаем векторное пространство которое чаще всего изучается в линейной алгебре, вещественном векторном пространстве R.

Если основанием операции возведения в степень является набор, операция возведения в степень - это декартово произведение, если не указано иное. Так как несколько декартовых произведений создают кортеж n- , который может быть представлен функцией на множестве соответствующей мощности, S становится просто набором всех функций от N до S в этом case:

$SN\; \equiv \; \{f:\; N\; \to \; S\}.\; \{\backslash \; displaystyle\; S\; ^\; \{N\}\; \backslash \; Equiv\; \backslash \; \{f\; \backslash \; двоеточие\; N\; \backslash \; к\; S\; \backslash \}.\}$

Это согласуется с возведением в степень кардинальных чисел в том смысле, что | S | = | S |, где | X | - мощность X. Когда "2" определяется как {0, 1}, мы имеем | 2 | = 2, где 2, обычно обозначаемое P (X), является набором мощности X; каждое подмножество Y в X однозначно соответствует функции на X, принимающей значение 1 для x ∈ Y и 0 для x ∉ Y.

В теории категорий

В Декартова закрытая категория, экспоненциальная операция может использоваться для возведения произвольного объекта в степень другого объекта. Это обобщает декартово произведение в категории множеств. Если 0 является начальным объектом в декартовой закрытой категории, то экспоненциальный объект 0 изоморфен любому конечному объекту 1.

Кардинальных и порядковых чисел

В теории множеств существуют экспоненциальные операции для кардинальных и порядковых чисел.

Если κ и λ являются кардинальными числами, выражение κ представляет мощность набор функций от любого набора мощности λ до любого набора мощности κ. Если κ и λ конечны, то это согласуется с обычной арифметической экспоненциальной операцией. Например, набор из 3-х элементов из 2-элементного набора имеет мощность 8 = 2. В кардинальной арифметике κ всегда равно 1 (даже если κ является бесконечным кардиналом или нулем).

Возведение в степень кардинальных чисел отличается от возведения в степень порядковых чисел, которое определяется процессом limit, включающим трансфинитную индукцию.

Так же, как возведение в степень натуральных чисел мотивировано повторным умножением, можно определить операцию, основанную на повторном возведении в степень; эту операцию иногда называют гипер-4 или тетрацией. Итерация тетрации приводит к другой операции и т.д., концепции под названием гипероперация. Эта последовательность операций выражается функцией Аккермана и нотацией стрелки вверх Кнута. Так же, как возведение в степень растет быстрее, чем умножение, которое растет быстрее, чем сложение, так и тетрация растет быстрее, чем возведение в степень. Вычисленные в (3, 3), функции сложения, умножения, возведения в степень и тетрации дают 6, 9, 27 и 7625597484987 (= 3 = 3 = 3) соответственно.

От нуля до степени нуля дает ряд примеров ограничений, которые имеют неопределенную форму 0. Пределы в этих примерах существуют, но имеют разные значения, показывая, что функция двух переменных x не имеет предела в точке (0, 0). Можно подумать, в каких точках эта функция имеет предел.

Точнее, рассмотрим функцию f (x, y) = x, определенную на D = {(x, y) ∈ R : x>0}. Тогда D можно рассматривать как подмножество R (то есть набор всех пар (x, y) с x, y, принадлежащих строке расширенных вещественных чисел R= [- ∞, + ∞], наделенный топологией произведения ), который будет содержать точки, в которых функция f имеет предел.

Фактически, f имеет предел во всех точках накопления D, за исключением (0, 0), (+ ∞, 0), (1, + ∞) и (1, −∞). Соответственно, это позволяет определять степени x по непрерывности всякий раз, когда 0 ≤ x ≤ + ∞, −∞ ≤ y ≤ + ∞, за исключением 0, (+ ∞), 1 и 1, которые остаются неопределенными формами.

При этом определении по непрерывности получаем:

• x = + ∞ и x = 0, когда 1 < x ≤ +∞.
• x = 0 и x = + ∞, когда 0 ≤ x < 1.
• 0 = 0 и (+ ∞) = + ∞, когда 0 < y ≤ +∞.
• 0 = + ∞ и (+ ∞) = 0, когда −∞ ≤ y < 0.

Эти степени получаются путем взятия пределов x для положительных значений x. Этот метод не позволяет определить x при x < 0, since pairs (x, y) with x < 0 are not accumulation points of D.

С другой стороны, когда n является целым числом, степень x уже имеет значение для всех значений x, включая отрицательные. Это может сделать определение 0 = + ∞, полученное выше для отрицательного n, проблематичным при нечетном n, поскольку в этом случае x → + ∞, когда x стремится к 0 через положительные значения, но не отрицательные.

Вычисление b с использованием повторного умножения требует n - 1 операции умножения, но его можно вычислить более эффективно, чем это, как показано в следующем примере. Чтобы вычислить 2, обратите внимание, что 100 = 64 + 32 + 4. Вычислите следующее в порядке:

1. 2 = 4
2. (2) = 2 = 16.
3. (2) = 2 = 256.
4. (2) = 2 = 65536.
5. (2) = 2 = 4294967296.
6. (2) = 2 = 18446744073709551616.
7. 2 2 2 = 2 = 1267650600228229401496703205376.

Для этой серии шагов требуется всего 8 операций умножения (последнее произведение выше требует 2 умножения) вместо 99.

Как правило, требуется количество операций умножения. для вычисления b можно уменьшить до Θ (log n), используя возведение в степень возведением в квадрат или (в более общем смысле) возведение в степень цепочки сложения. Нахождение минимальной последовательности умножений (цепочки сложения минимальной длины для экспоненты) для b является сложной задачей, для которой в настоящее время не известны эффективные алгоритмы (см. Задача суммы подмножеств ), но существует множество достаточно эффективных эвристических методов. доступны алгоритмы.

Размещение целочисленного надстрочного индекса после имени или символа функции, как если бы функция возводилась в степень, обычно относится к повторяющимся композиция функции, а не повторное умножение. Таким образом, f (x) может означать f (f (f (x))); в частности, f (x) обычно обозначает обратную функцию для f. Это обозначение было введено Гансом Генрихом Бюрманном и Джоном Фредериком Уильямом Гершелем. Итерированные функции представляют интерес при изучении фракталов и динамические системы. Бэббидж был первым, кто изучал проблему поиска функционального квадратного корня f (x).

Чтобы отличить возведение в степень от композиции функции, обычно используют экспоненту после круглой скобки, заключающей аргумент функции; то есть f (x) означает (f (x)), а f (x) означает 1 / f (x).

По историческим причинам и из-за неоднозначности, возникающей из-за того, что аргументы не заключаются в круглые скобки, верхний индекс после имени функции, применяемый специально к тригонометрическим и гиперболическим функциям отклоняющееся значение: положительный показатель степени, примененный к сокращению функции, означает, что результат возведен в эту степень, в то время как показатель степени -1 все еще обозначает обратную функцию. То есть sin x - это просто сокращенный способ записи (sin x) = sin (x) без использования круглых скобок, тогда как sin x относится к обратной функции sine, также называемой arcsin x. Каждая тригонометрическая и гиперболическая функция имеет собственное имя и аббревиатуру как для обратной (например, 1 / (sin x) = (sin x) = sin (x) = csc x), так и для обратной (например, cosh x = arcosh Икс). Аналогичное соглашение существует для логарифмов, где сегодня log x обычно означает (log x), а не log log x.

Чтобы избежать двусмысленности, некоторые математики предпочитают использовать ∘ для обозначения композиционного значения, записывая f (x) для n-й итерации функции f (x), как, например, f (x), означающее f (f (f (x))). Для той же цели f (x) использовался Бенджамином Пирсом, тогда как Альфред Прингсхайм и Жюль Молк предложил вместо него f (x).

В языках программирования возведение в степень обычно выражается либо как инфиксный оператор, либо как (префиксная) функция, поскольку они являются линейными обозначениями, которые не поддерживают надстрочные символы:

• x ↑ y: Алгол, Commodore BASIC, TRS-80 Level II / III BASIC.
• x ^ y: AWK, BASIC, J, MATLAB, Wolfram Language (Mathematica ), R, Microsoft Excel, Analytica, TeX ( и его производные), TI-BASIC, bc (для целочисленных показателей), Haskell (для неотрицательных целочисленных показателей), Lua и большинство систем компьютерной алгебры. Противоречивое использование символа ^включает: XOR (в арифметическом расширении оболочки POSIX, AWK, C, C ++, C #, D, Go, Java, JavaScript, Perl, PHP, Python, Ruby и Tcl), косвенное обращение (Pascal) и конкатенация строк (OCaml и Standard ML).
• x ^^ y: Haskell (для дробного основания, целочисленные показатели), D.
• x ** y: Ada, Z shell, KornShell, Bash, COBOL, CoffeeScript, Fortran, FoxPro, Gnuplot, Groovy, JavaScript, OCaml, F#, Perl, PHP, PL / I, Python, Rexx, Ruby, SAS, Seed7, Tcl, ABAP, Mercury, Haskell (для показателей с плавающей запятой), Тьюринг, VHDL.
• pown xy: F # (для целочисленного основания, целочисленной степени).
• x⋆y: APL.

Многие другие в языках программирования отсутствует синтаксическая поддержка возведения в степень, но они предоставляют библиотечные функции tions:

• pow (x, y): C, C ++.
• Math.Pow (x, y): C#.
• math: pow (X, Y): Erlang.
• Math. pow (x, y): Java.
• [Math] :: Pow (x, y): PowerShell.

Для некоторых показателей степени существуют особые способы вычислить много x быстрее, чем с помощью общего возведения в степень. Эти случаи включают небольшие положительные и отрицательные целые числа (предпочитают x · x над x; предпочитают 1 / x над x) и корни (предпочитают sqrt (x) над x, предпочитают cbrt (x) над x).

Не все языки программирования придерживаются одного и того же соглашения об ассоциации для возведения в степень: в то время как язык Wolfram, Google Search и другие используют правильные ассоциации (т. Е. a ^ b ^ cоценивается как a ^ (b ^ c)), многие компьютерные программы, такие как Microsoft Office Excel и Matlab, связаны с слева (т.е. a ^ b ^ cоценивается как (a ^ b) ^ c).

• Портал математики

• Двойная экспоненциальная функция
• Экспоненциальный спад
• Экспоненциальное поле
• Экспоненциальный рост
• Список экспоненциальных тем
• Модульное возведение в степень
• Научное нотация
• Подстрочные и верхние индексы Unicode
• x = y
• Ноль в степени нуля

• «Представляем 0-ю степень». PlanetMath.
• Законы экспонентов с выводом и примерами