| Виды углов |
|---|
| 2D углы |
| Внешний вид |
| 2D угловые пары |
| Смежные Вертикальные Дополняющие Дополняющие Поперечный |
| 3D углы |
| Двугранный |
|
 Прямой угол равен 90 градусам.
Прямой угол равен 90 градусам.  Отрезок (AB), нарисованный так, что он образует прямые углы с линией (CD).
Отрезок (AB), нарисованный так, что он образует прямые углы с линией (CD). В геометрии и тригонометрии, А под прямым углом является углом ровно 90 градусов или л / 2 радиана, соответствующих четверть поворота. Если луч размещен так, что его конечная точка находится на прямой, а прилегающие углы равны, то это прямые углы. Термин является калькой из латинского Angulus прямой мышцы ; здесь rectus означает «вертикально», имея в виду вертикальный перпендикуляр к горизонтальной базовой линии.
Тесно связанные и важные геометрические концепции - это перпендикулярные линии, означающие, что линии, образующие прямые углы в точке их пересечения, и ортогональность, которая является свойством образования прямых углов, обычно применяется к векторам. Наличие прямого угла в треугольнике является определяющим фактором для прямоугольных треугольников, что делает прямой угол основным для тригонометрии.
Значение «прямо» в « прямом угле», возможно, относится к латинскому прилагательному rectus, которое можно перевести как прямое, прямое, вертикальное или перпендикулярное. Греческий эквивалент Orthos, что означает прямой или перпендикулярно (см ортогональность ).
Прямоугольник представляет собой четырехугольник с четырьмя прямыми углами. У квадрата есть четыре прямых угла, помимо сторон равной длины.
Теорема Пифагора утверждает, как определить, когда треугольник является прямоугольным.
 Прямой треугольник с прямым углом, показанным через небольшой квадрат.
Прямой треугольник с прямым углом, показанным через небольшой квадрат. 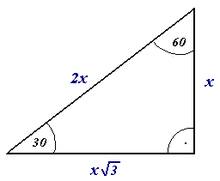 Другой вариант схематического обозначения прямого угла с помощью угловой кривой и маленькой точки.
Другой вариант схематического обозначения прямого угла с помощью угловой кривой и маленькой точки. В Юникоде символ прямого угла - U + 221F ∟ ПРАВЫЙ УГОЛ (HTML amp;#8735; amp;angrt;). Его не следует путать с символом аналогичной формы U + 231E ⌞ НИЖНИЙ ЛЕВЫЙ УГОЛ (HTML amp;#8990; amp;dlcorn;, amp;llcorner;). Связанные символы: U + 22BE ⊾ ПРАВЫЙ УГОЛ С ДУГОМ (HTML amp;#8894; amp;angrtvb;), U + 299C ⦜ ВАРИАНТ ПРАВЫЙ УГОЛ С КВАДРАТОМ (HTML amp;#10652; amp;vangrt;) и U + 299D ⦝ ИЗМЕРЕНИЕ ПРАВЫЙ УГОЛ С ТОЧКОЙ (HTML amp;#10653; amp;angrtvbd;).
На диаграммах тот факт, что угол является прямым углом, обычно выражается добавлением небольшого прямого угла, который образует квадрат с углом на диаграмме, как видно на диаграмме прямоугольного треугольника (в британском английском, прямоугольный треугольник) вправо. Символ измеренного угла - дуга с точкой - используется в некоторых европейских странах, включая немецкоязычные страны и Польшу, в качестве альтернативного символа прямого угла.
Прямые углы являются фундаментальными в «Элементах» Евклида. Они определены в Книге 1, определение 10, в котором также определены перпендикулярные линии. Определение 10 не использует числовые измерения в градусах, а касается самой сути того, что такое прямой угол, а именно двух прямых линий, пересекающихся, чтобы образовать два равных и смежных угла. Прямые, образующие прямые углы, называются перпендикулярными. Евклид использует прямые углы в определениях 11 и 12 для определения острых углов (меньших прямого угла) и тупых углов (тех, которые больше прямого). Два угла называются дополнительными, если их сумма составляет прямой угол.
Книга 1 Постулат 4 гласит, что все прямые углы равны, что позволяет Евклиду использовать прямой угол как единицу измерения других углов. Комментатор Евклида Прокл дал доказательство этого постулата, используя предыдущие постулаты, но можно утверждать, что это доказательство использует некоторые скрытые предположения. Саккери также дал доказательство, но с более явным предположением. В гильбертовом «S аксиоматики геометрии это утверждение дается в виде теоремы, но только после того, как много наработок. Кто-то может возразить, что, даже если постулат 4 может быть доказан на основе предыдущих, в том порядке, в котором Евклид представляет свой материал, необходимо включить его, поскольку без него постулат 5, который использует прямой угол в качестве единицы измерения, не дает смысл.
Прямой угол может быть выражен в разных единицах:
На протяжении всей истории плотники и каменщики знали быстрый способ подтвердить, является ли угол истинным «прямым». В его основе лежит наиболее широко известная тройка Пифагора (3, 4, 5) и так называемое «правило 3-4-5». От рассматриваемого угла, если провести прямую линию вдоль одной стороны ровно на 3 единицы длины, а вдоль второй стороны ровно на 4 единицы длины, получится гипотенуза (более длинная линия напротив прямого угла, соединяющего две измеренные конечные точки). ровно 5 единиц в длину. Это измерение может быть выполнено быстро и без технических инструментов. Геометрический закон, лежащий в основе измерения, - это теорема Пифагора («Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов двух смежных сторон»).
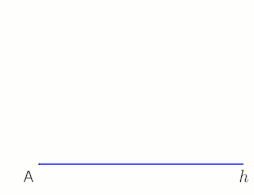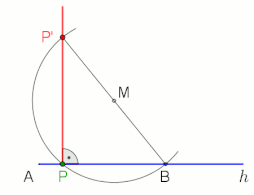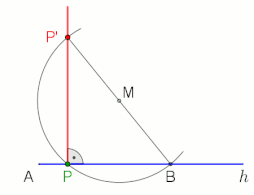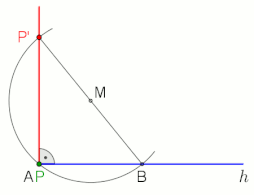 Построение перпендикуляра к полуоси h из точки P (применимо не только в конечной точке A, M выбирается произвольно), анимация в конце с паузой 10 с
Построение перпендикуляра к полуоси h из точки P (применимо не только в конечной точке A, M выбирается произвольно), анимация в конце с паузой 10 с  Альтернативное построение, если P за пределами полуоси h и расстояние от A до P 'небольшое (B выбирается свободно), анимация в конце с паузой 10 с Основная статья: теорема Фалеса
Альтернативное построение, если P за пределами полуоси h и расстояние от A до P 'небольшое (B выбирается свободно), анимация в конце с паузой 10 с Основная статья: теорема Фалеса Теорема Фалеса утверждает, что угол, вписанный в полукруг (с вершиной на полукруге и определяющими лучами, проходящими через концы полукруга), является прямым углом.
Два примера применения, в которые включены прямой угол и теорема Фалеса (см. Анимацию).