 Отрезок AB перпендикулярен сегменту CD, поскольку два угла, которые он создает (обозначены оранжевым и синим), составляют каждый по 90 градусов. Отрезок AB можно назвать перпендикуляром от A к отрезку CD, используя слово «перпендикуляр» как существительное. Точка B называется основанием перпендикуляра от A до сегмента CD или просто основанием A на CD.
Отрезок AB перпендикулярен сегменту CD, поскольку два угла, которые он создает (обозначены оранжевым и синим), составляют каждый по 90 градусов. Отрезок AB можно назвать перпендикуляром от A к отрезку CD, используя слово «перпендикуляр» как существительное. Точка B называется основанием перпендикуляра от A до сегмента CD или просто основанием A на CD. В элементарной геометрии свойство быть перпендикуляром (перпендикулярность ) - это отношение между двумя линиями , которые встречаются под прямым углом (90 градусов ). Свойство распространяется на другие связанные геометрические объекты.
Линия считается перпендикулярной другой линии, если две прямые пересекаются под прямым углом. Явно первая линия перпендикулярна второй линии, если (1) две линии встречаются; и (2) в точке пересечения прямой угол на одной стороне первой линии разрезается второй линией на два конгруэнтных угла. Можно показать, что перпендикулярность является симметричной, то есть если первая линия перпендикулярна второй линии, то вторая линия также перпендикулярна первой. По этой причине мы можем говорить о двух линиях как о перпендикулярных (друг другу) без указания порядка.
Перпендикулярность легко распространяется на сегменты и лучи. Например, отрезок линии 


Линия считается перпендикулярной плоскости , если она перпендикулярна каждой линии в плоскости, которую она пересекает. Это определение зависит от определения перпендикулярности между линиями.
Две плоскости в пространстве называются перпендикулярными, если двугранный угол, под которым они встречаются, является прямым углом (90 градусов).
Перпендикулярность - это частный пример более общей математической концепции ортогональности ; перпендикулярность - это ортогональность классических геометрических объектов. Таким образом, в высшей математике слово «перпендикуляр» иногда используется для описания гораздо более сложных геометрических условий ортогональности, например, между поверхностью и ее нормалью.
Слово стопа часто используется в связи с перпендикулярами. Это использование проиллюстрировано на верхней диаграмме выше и в ее заголовке. Схема может быть в любой ориентации. Стопа не обязательно внизу.
Точнее, пусть A будет точкой, а m - прямой. Если B - точка пересечения m и единственной прямой, проходящей через A, которая перпендикулярна m, то B называется основанием этого перпендикуляра, проходящего через A.
 Построение перпендикуляра (синий) к линии AB через точку P.
Построение перпендикуляра (синий) к линии AB через точку P. 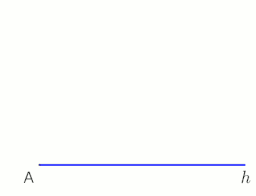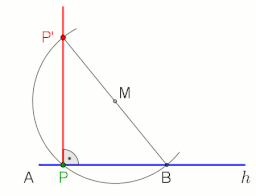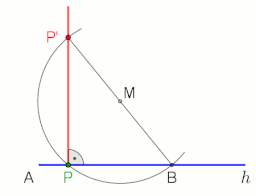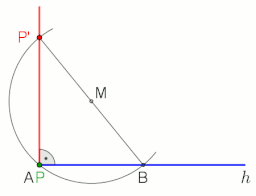 Построение перпендикуляра к полуоси h из точки P (применимо не только в конечной точке A, M выбирается произвольно), анимация в конце с паузой 10 с
Построение перпендикуляра к полуоси h из точки P (применимо не только в конечной точке A, M выбирается произвольно), анимация в конце с паузой 10 с Чтобы провести перпендикуляр к линии AB через точку P с помощью построения циркуля и линейки, действуйте следующим образом (см. Рисунок слева):
Чтобы доказать, что PQ перпендикулярен AB, используйте теорему сравнения SSS для 'и QPB', чтобы сделать вывод, что углы OPA 'и OPB' равны. Затем используйте теорему сравнения SAS для треугольников OPA 'и OPB', чтобы сделать вывод, что углы POA и POB равны.
Чтобы провести перпендикуляр к линии g в точке P или через нее, используя теорему Фалеса, см. Анимацию справа.
Теорема Пифагора может быть использована как основа методов построения прямых углов. Например, посчитав звенья, можно сделать три отрезка цепи с длинами в соотношении 3: 4: 5. Их можно выложить в виде треугольника, у которого будет прямой угол напротив его самой длинной стороны. Этот метод полезен для разбивки садов и полей, где размеры велики и не требуется большой точности. Цепи можно использовать повторно, когда это необходимо.
 Знаки стрелок указывают на то, что линии a и b, отрезанные поперечной линией c, параллельны.
Знаки стрелок указывают на то, что линии a и b, отрезанные поперечной линией c, параллельны. Если две прямые (a и б) оба перпендикулярны третьей линии (в), все углы, образованные вдоль третьей линии, являются прямыми углами. Следовательно, в евклидовой геометрии любые две прямые, которые обе перпендикулярны третьей линии, параллельны друг другу из-за постулата параллельности. И наоборот, если одна линия перпендикулярна второй линии, она также перпендикулярна любой линии, параллельной этой второй линии.
На рисунке справа все углы, заштрихованные оранжевым, конгруэнтны друг другу, а все углы, заштрихованные зеленым, конгруэнтны друг другу, поскольку вертикальные углы совпадают и чередующиеся внутренние углы, образованные поперечными параллельными линиями разреза, совпадают. Следовательно, если прямые a и b параллельны, любой из следующих выводов приводит ко всем остальным:
Расстояние от точки до линии - это расстояние до ближайшей точки на этой линии. Это точка, в которой отрезок от нее до данной точки перпендикулярен прямой.
Аналогично, расстояние от точки до кривой измеряется отрезком линии, перпендикулярным касательной линии к кривой в ближайшей точке на кривая.
Перпендикулярная регрессия подгоняет линию к точкам данных за счет минимизации суммы квадратов перпендикулярных расстояний от точек данных до линии.
Расстояние от точки до плоскости измеряется как длина от точки вдоль сегмента, перпендикулярного плоскости, то есть перпендикулярно всем линиям в плоскости, которые пройти через ближайшую точку на плоскости к данной точке.
В двумерной плоскости прямые углы могут быть образованы двумя пересекающимися линиями, если произведение их наклонов равно −1. Таким образом, определяя две линейные функции : y 1 = a 1 x + b 1 и y 2 = a 2 x + b 2, графики функций будут перпендикулярны и образуют четыре прямых угла в местах пересечения линий, если a 1a2= −1. Однако этот метод нельзя использовать, если наклон равен нулю или не определен (линия параллельна оси).
Для другого метода пусть две линейные функции имеют вид: a 1 x + b 1 y + c 1 = 0 и a 2 x + b 2 y + c 2 = 0. Линии будут перпендикулярными тогда и только тогда, когда a 1a2+ b 1b2= 0. Этот метод упрощен из скалярного произведения (или, в более общем смысле, внутреннего произведения ) векторов . В частности, два вектора считаются ортогональными, если их внутренний продукт равен нулю.
Каждый диаметр круга окружности перпендикулярен касательной . к этой окружности в точке, где диаметр пересекает окружность.
Отрезок, проходящий через центр окружности пополам хорду, перпендикулярен хорде.
Если пересечение любых двух перпендикулярных хорд делит одну хорду на длины a и b и делит другую хорду на длины c и d, то a + b + c + d равно квадрату диаметра.
Сумма квадратов длин любых двух перпендикулярных хорд, пересекающихся в данной точке, такая же, как и у любых других двух перпендикулярных хорд, пересекающихся в той же точке, и задается формулой 8r - 4p (где r - длина окружности радиус, а p - расстояние от центральной точки до точки пересечения).
Теорема Фалеса утверждает, что две прямые, проходящие через одну и ту же точку на окружности, но проходящие через противоположные конечные точки диаметра, перпендикулярны. Это эквивалентно тому, что любой диаметр окружности образует прямой угол в любой точке окружности, кроме двух конечных точек диаметра.
Большая и малая оси эллипса перпендикулярны друг другу и касательным линиям к эллипсу в точках, где оси пересекают эллипс.
Большая ось эллипса перпендикулярна направляющей и каждой прямой кишке.
в параболе ось симметрии перпендикулярна прямой кишке, директрисе и касательной в точке, где ось пересекает параболу.
От точки на касательной к вершине параболы другая касательная линия к параболе перпендикулярна прямой, идущей от этой точки через фокус параболы.
ортоптическое свойство параболы заключается в том, что если две касательные к параболе перпендикулярны друг другу, то они пересекаются по направляющей. И наоборот, две касательные, пересекающиеся на директрисе, перпендикулярны. Это означает, что если смотреть из любой точки на своей директрисе, любая парабола имеет прямой угол.
Поперечная ось гиперболы перпендикулярна сопряженной оси и каждой направляющей.
Произведение перпендикулярных расстояний от точки P на гиперболе или на ее сопряженной гиперболе до асимптот является константой, не зависящей от местоположения P.
A прямоугольная гипербола имеет асимптоты, которые перпендикулярны друг другу. Его эксцентриситет равен
Катеты прямоугольного треугольника перпендикулярны друг другу.
высоты треугольника перпендикулярны их соответствующим основаниям. серединные перпендикуляры сторон также играют важную роль в геометрии треугольника.
Линия Эйлера равнобедренного треугольника перпендикулярна основанию треугольника.
Теорема о прямой линии Дроза-Фарни касается свойства двух перпендикулярных прямых, пересекающихся в ортоцентре.
Теорема Харкурта касается отношения отрезков прямой через вершина и перпендикулярна любой прямой касательной к треугольнику , вписанной в круг.
в квадрате или другом прямоугольнике , все пары смежных сторон перпендикулярны. Правая трапеция - это трапеция , имеющая две пары смежных сторон, перпендикулярных.
Каждая из четырех солодов четырехугольника является перпендикуляром к стороне, проходящей через среднюю точку противоположной стороны.
Ортодиагональный четырехугольник - это четырехугольник, диагонали перпендикулярны. К ним относятся квадрат, ромб и воздушный змей. Согласно теореме Брахмагупты в ортодиагональном четырехугольнике, который также является циклическим, линия, проходящая через середину одной стороны и точку пересечения диагоналей, перпендикулярна противоположной стороне.
Согласно теореме ван Обеля, если квадраты построены снаружи по сторонам четырехугольника, отрезки прямых, соединяющие центры противоположных квадратов, перпендикулярны и равны по длине.
До трех линий в трехмерном пространстве могут быть попарно перпендикулярны, например, оси x, y и z трех -мерная декартова система координат.
| Посмотрите вверх перпендикулярно в Викисловаре, бесплатный словарь. |